自主车辆高效滚动时域轨迹规划与跟踪控制

2021-01-23何德峰徐广琪李海平

浙江工业大学学报 2021年1期

何德峰，徐广琪，李海平

(浙江工业大学信息工程学院，浙江杭州 310023)

自主车辆是当前学术界和工业界的研究热点之一，其研究成果的应用可以大幅减少因人为驾驶失误造成的交通事故，提高车辆行驶安全和道路通行效率[1]，其中，轨迹规划与跟踪控制是自主车辆研究的核心。用于轨迹规划的人工势场法已在机器人领域的研究中被广泛应用于避障[2]，相较于随机搜索[3]、栅格网络[4]和模糊控制[5]等方法，其算法结构简单、轨迹圆滑。对于自动驾驶的高速公路车辆，需要处理各种各样的驾驶场景，除安全避开障碍物到达目标点外，还应考虑道路结构。Wolf等[6]对高速公路上行驶的自主车辆行车环境进行势场建模，通过梯度下降法规划路径。Jie等[7]提出轨迹规划与跟踪框架，将路径跟踪任务阐述为多约束模型预测问题，考虑道路的几何约束和车辆的动态约束，计算车辆转向角以跟踪规划的轨迹来避开障碍物，但研究中未考虑车辆特性，车辆可能跟踪不上规划的轨迹。在轨迹规划的同时应考虑车辆动力学、运动学特性以及轮胎和执行器的限制，使规划的路径更易于自主车辆跟踪。Rasekhipour等[8-9]用车辆与障碍物间的符号距离(SD)来建立势场函数，并将势场函数添加进模型预测控制器的目标函数中，基于障碍物和道路结构以及车辆动力学规划最佳行车轨迹，在跟踪全局路径的同时实现避障。Wang等[10]将潜在碰撞严重度指数PCSI也添加进模型预测控制器的目标函数中，当碰撞不可避免时，规划尽可能减少碰撞损失的轨迹。在轨迹规划与跟踪控制中，通常使用人工势场法基于障碍物、道路结构和目标势场函数生成势场，沿势场的下降方向移动来规划路径。然后，路径跟踪模块计算跟踪路径所需的车辆输入量[8-12]。Huang等[13]首次提出人工势场和模型预测控制组合控制器，该控制器的突出优点是可以同时处理轨迹规划与跟踪控制问题；缺点是采用较简单的车辆运动学模型，自主车辆的跟踪控制精度有待提升。徐扬等[14]在此基础上，基于车辆动力学模型提出一种针对自主车辆轨迹规划与跟踪控制的统一建模方法，但求解非凸非线性优化问题计算成本高，不能保证系统实时性。Rasekhipour等[8-9]对不可穿越的障碍物考虑双曲势场函数，对可穿越的障碍物考虑指数势场函数，通过凸二次函数逼近非线性势场函数，从而使模型预测控制优化问题转化为凸二次规划问题，减少了计算成本。Jiang等[15]利用障碍物信息生成单维人工势场(SDAPF)，将优化问题转换为凸二次规划来减少计算量，但仅考虑单一障碍物势场，且不包括道路结构。由于势场函数的特性以及动力学模型的复杂性，传统模型预测控制优化问题可能非常耗时，就实时避障系统而言，解决模型预测优化问题需要更高效的算法和更少的计算时间。

笔者针对结构化道路上行驶的自主车辆轨迹规划与跟踪控制问题，提出一种基于模型预测控制的自主车辆高效滚动时域轨迹规划与跟踪控制方法。通过人工势场法为不同障碍物和道路结构分配不同的势场函数，再将这些表征安全性的势场函数作为轨迹规划与跟踪模型预测控制的优化目标函数，同时考虑车辆动力学特性、运动学约束和舒适性要求，使规划的轨迹易于车辆跟踪。但由于势场函数的非凸和非线性，轨迹规划和跟踪模型预测控制的在线优化计算量大，难以满足自主车辆跟踪控制的实时性要求。特别地，模型预测控制的计算量通常随控制变量的维数呈指数级增加，因此，引入阶梯式控制策略，参数化预测时域内的控制输入增量，压缩优化问题的优化变量个数，从而降低模型预测控制的在线计算量。针对典型交通场景进行Carsim与Matlab/Simulink联合仿真，结果表明了该方法的有效性以及优越的实时性能。

1 轨迹规划与跟踪系统描述

1.1 用于控制的车辆动力学模型

选择自行车模型对车辆动力学进行建模，车辆模型相关符号如图1所示。

图1 自行车模型

车辆动力学方程式可描述为

m×ax=FxT

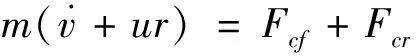
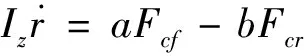
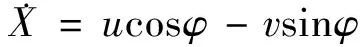
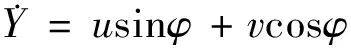
(1)

式中：X，Y，φ分别为车辆在全局坐标系下的纵向位置、横向位置、横摆角；u，v，r分别为车辆在质心处的纵向速度、横向速度、横摆角速度；m为整车质量；Iz为车辆绕其z轴的转动惯量；Fcf和Fcr分别为前后轮胎的侧向力；FxT为轮胎总纵向力。

笔者基于小角度假设和线性轮胎模型计算轮胎侧向力[16]，即在轮胎力的计算过程中满足cosθ≈1，sinθ≈θ，tanθ=θ，其中θ表示各个角，包括前轮偏角和前、后轮侧偏角等，由此简化得到轮胎侧向力方程为

(2)

式中：a和b分别为车辆质心到前、后轴的距离；δf为前轮转向角；αf和αr分别为车辆前、后轮胎侧偏角；Ccf和Ccr分别表示前、后轮的侧偏刚度，其计算方法参见Gao等[17]的研究成果。笔者直接在Carsim中调取所选车辆模型的轮胎侧向力随侧偏角变化曲线计算前后轮的侧偏刚度。

综上，自主车辆动力学特性的非线性模型可表示为

(3)

1.2 自主车辆结构化道路行车环境的势场函数

势场函数的功能是为了使自主车辆避开危险障碍物和道路边缘，同时尽量保持在车道中心并以所需速度朝着目标点行驶。在无障碍的情况下，自主车辆应保持期望速度在当前车道中央行驶。当接近同一车道的前方静止障碍车辆或慢速障碍车辆时，应考虑绕开障碍车辆再回到原车道或换道以避开慢速车辆。

定义道路、障碍车辆和目标点信息生成自主车辆总势场UAPF为

UAPF=Ulane+Uroad+Uob-car+Ugoal

(4)

式中：Ulane描述分道线排斥势场；Uroad描述道路边界线排斥势场，描述其他障碍物排斥的势场函数可能也包含在Uob-car内，笔者主要描述自动驾驶中最常见的车辆障碍；Ugoal描述目标点引导势场。

1.2.1 分道线势场

分道线势场作用是使车辆在车道内安全行驶，同时允许车辆在避开障碍物过程中越过分道线。总的分道线势场为各个分道线势场的叠加，可表示为

(5)

式中Ulane为第i个车道到第Nlane个车道的总分道线势场。车辆和分道线之间的距离的类高斯函数用于描述由分道线引起的势场[6]，可表示为

(6)

式中：Alane为分道线势场强度参数；σlane为势场值收敛系数，大小与道路宽度正相关；ylane,i为第i条道路分道线的位置。选取的势场函数在分道线处取最大值，往两边减少，同时整体是一个比较小的值，以确保车辆有换道需求时可跨越。宽为8 m的两车道道路分界线的Y轴横截面势场分布情况如图2所示。

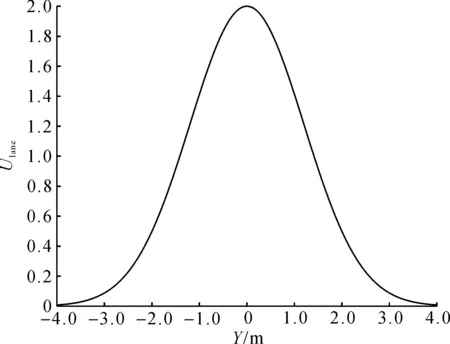
图2 分道线势场

1.2.2 道路边界线

当自主车辆在道路上行驶，应该避免碰撞到道路边界或道路隔离带，以避免车祸发生。道路边界势场[6]用幂函数可表示为

(7)

式中：Aroad为道路边界势场强度；yroad,j为第i条道路边界位置。在靠近道路边界的地方，势场梯度急剧增大，如道路边界道在y=4和y=-4处，道路总势场Y轴横截面如图3所示。

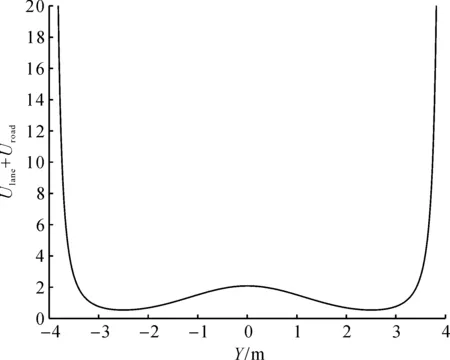
图3 道路势场

1.2.3 障碍车势场

通过障碍车势场建立来使自主车辆与周围障碍车辆保持安全距离。将阻碍自主车辆进行换道、超车等行为的其他车辆统称为障碍车辆。障碍车势场分布如图4所示，在障碍车后方建立三角形安全区域，避免碰撞的同时引导自主车辆从后方换道。图4中安全距离S定义为S=τVr+Smin，式中：τ为传感器采样时延；Vr为自主车辆与障碍车辆之间的相对速度；Smin为最小安全距离。在障碍车前方建立矩形安全区域，使自主车辆换回原车道时与障碍车保持一段安全距离s，计算式为s=ξV+Smin，式中参数ξ与障碍车辆的速度V正相关。

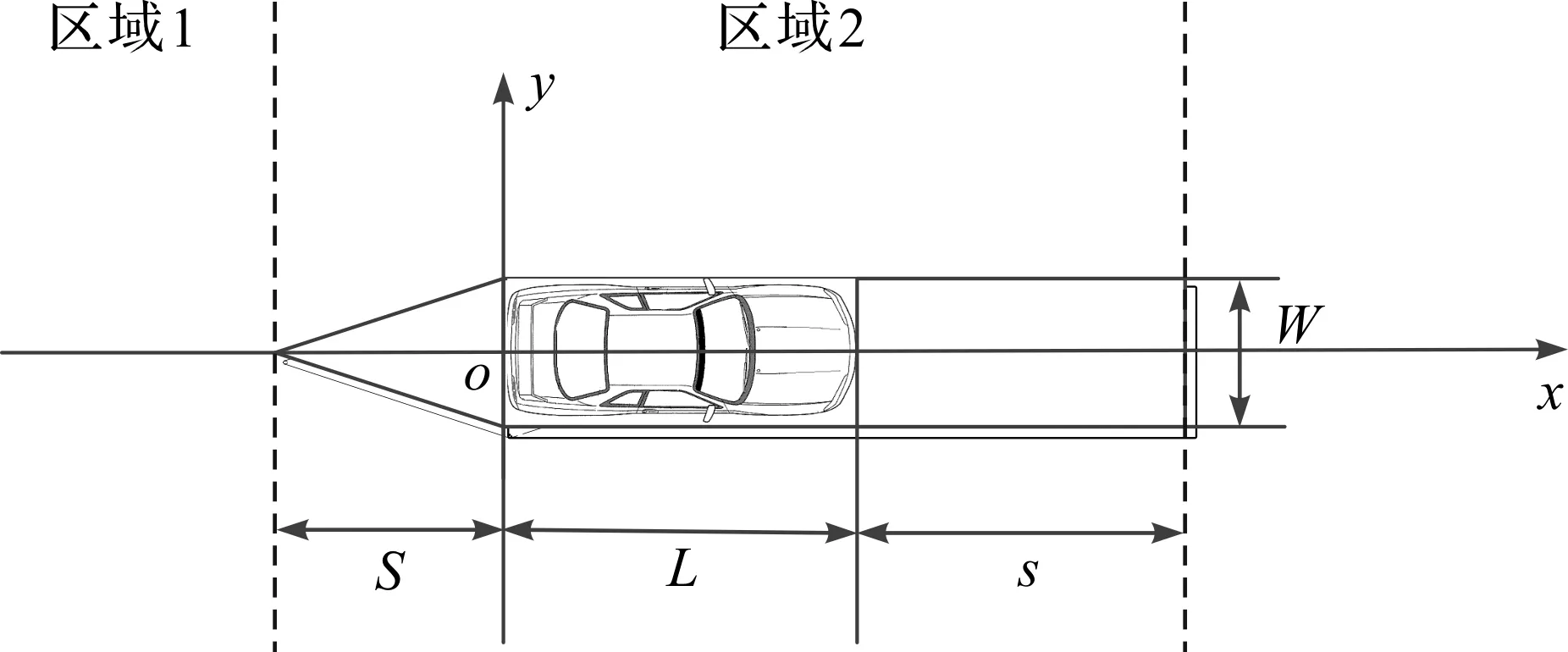
图4 障碍车势场分布

当障碍车辆的速度大于被控自主车辆时，不需要改变被控自主车辆的行驶状态，此时障碍车势场为零。下面讨论用于描述相对速度大于零情况下的障碍车辆的势场函数。第m辆障碍车辆总势场被认为是纵向势场在横向势场上的延伸[13]，纵向势场和横向势场分别为

Uob-car,m(X,Y)=Uob-car,lo·Uob-car,la

(8)

(9)

式中：Acar为车辆在区域2时纵向势场，在区域1时用汤川势函数[6]来描述障碍车势场；Acar,lo为纵向势场强度参数；K为自主车辆与障碍车辆之间的纵向距离。横向势场用类高斯函数[12]可表示为

(10)

式中：D为自主车辆与障碍车辆之间的横向距离；σob-car为车辆横向势场收敛系数，其值由车道宽决定。

1.2.4 目标点势场

目标点势场的作用是引导车辆向目标点行驶，所以整体是一个大于零的较小值。选取一次函数来描述目标点势场[14]为

Ugoal(X,Y)=ε-β×(xgoal-X)

(11)

式中xgoal为目标点纵向位置。

2 滚动时域轨迹规划与跟踪控制

考虑车辆动力学非线性模型(3)，定义状态量x=[φ,μ,v,r,X,Y]T和输入量u=[δf,ax]T，得到状态方程为

(12)

通过零阶保持器离散化系统(12)，得到的方程式为

x(k+1)=x(k)+Tsf(x(k),u(k))

(13)

式中Ts为采样时间。

自主车辆在势场的引导下，避开障碍物并沿着势场下降的方向到达目标点，规划的局部路径为预测控制算法寻找的势场中势场值低的点。势场值在一定程度上表示行车风险，通过自主车辆总势场值的大小可以非常直观地判断出各个位置行车危险程度的大小。将描述障碍车辆、道路规则以及目标点的势场函数添加到模型预测控制器的目标函数中，得到

(14)

为保证自主车辆乘员的舒适性，加速度增量和前轮转角变化率应满足约束条件

Δax_min≤Δax(k+i|k)≤Δax_max

Δδf_min≤Δδf(k+i|k)≤Δδf_max

(15)

式中：Δδf为一次采样步骤中前轮转角的变化量；●min和●max分别为各自变量的最小和最大极限值。同时，控制输入量同样需要满足约束条件

umin≤u(k+i|k)≤umax

(16)

式中：umin和umax分别为控制输入的最小和最大极限值。车辆的操纵稳定性直接影响到车辆的行驶安全[18-19]，因此在一定的路面附着系数下，所允许的轮胎侧偏角应该满足αf,r_min≤αf,r≤αf,r_max。

将自主车辆的轨迹规划与跟踪控制问题转化为有限时域内的约束优化控制问题。模型预测控制器在每个采样时刻Ts在线求解一个带约束的优化控制问题，其在线计算时间直接关系到控制器的运行效果。自主车辆行驶系统需要满足快速性要求，但由于非线性非凸势场函数，优化问题是非线性非凸的，在线计算成本很高。为了提高预测控制效果得到光滑平稳无碰撞路径，往往需要较大的预测时域，且决策变量的维数等于预测时域Np和控制变量个数n的乘积，更加加大了优化问题计算时间，难以满足快速系统实时性要求。为减小极小化目标函数式(14)的在线计算量，引入阶梯式控制策略。考虑当前时刻k，对预测时域Np步内的控制输入增量做阶梯式参数化[20-26]，即

Δu(k+i|k)=λΔu(k+i-1|k)=

λiΔu(k|k)i=0, 1, 2, …,Np-1

(17)

式中：Δu(k|k)为当前时刻k控制增量；λ为梯度因子。当0<λ<1，表示未来预测时域内控制增量逐渐减小；当λ>1，表示未来预测时域内控制量增量逐渐增大。考虑第j个控制变量(j=1，2，…，n)，即ax=u1，δf=u2，预测时域Np内的预测量为

uj(k|k)=uj(k-1|k)+Δuj(k|k)

uj(k+1|k)=uj(k|k)+Δuj(k+1|k)=

uj(k-1|k)+Δuj(k|k)+λjΔuj(k|k)

…

uj(k+Np-1|k)=

uj(k+Np-2|k)+Δuj(k+Np-1|k)=

uj(k-1|k)+Δuj(k|k)+…+

(18)

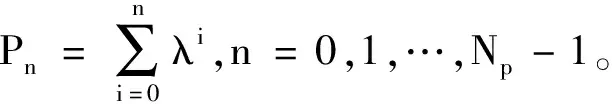
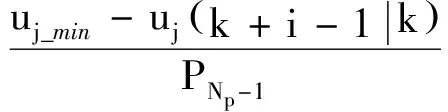
(19)

式中uj(k-1|k)为时刻k-1作用于系统的实际控制量。结合式(15)整理得

Δuj_min≤Δuj(k+i|k)≤Δuj_maxλ<1

(20)

进一步结合式(19，20)，得到第j个控制量增量Δuj(k+i|k)在预测时域Np内的最终约束范围为

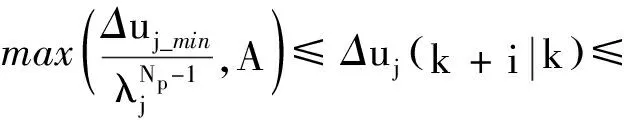
max(Δuj_min,A)≤Δuj(k+i|k)≤

min(Δuj_max,B)λ<1

(21)

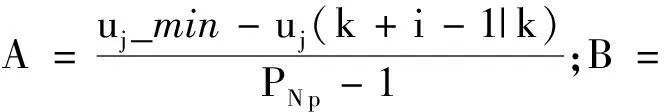
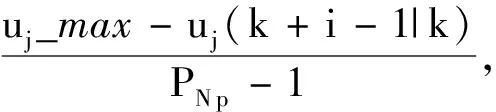
将式(17)代入式(14)得

(22)

对二维输入的系统进行Np步预测时，采用阶梯式控制策略，可将决策变量的数量由2Np减少至2 个，有利于在预测时域较长时有效降低在线计算量。因此，自主车辆的高效滚动时域路径规划与跟踪控制问题可定义为

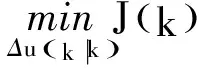
s.t.(i=0, 1, 2, …,Np-1)

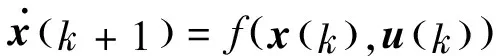
u(k+i|k)=u(k+i-1|k)+λiΔu(k|k)

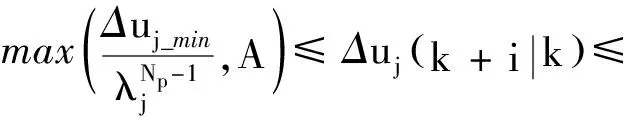
max(Δuj_min,A)≤Δuj(k+i|k)≤

min(Δuj_max,B)λ<1

αf,r_min≤αf,r(k+i|k)≤αf,r_max

(23)

在线计算时刻k最优控制输入算法步骤为

Step1设置轨迹规划与跟踪控制器离线参数：加权矩阵Q，R，S，W，采样时间Ts，预测时域Np，阶梯因子λ，初始控制量u(0)。

Step2在采样时刻k，在线计算优化问题式(23)，得控制增量序列[Δu(k|k)，Δu(k+1|k)，…，Δu(k+Np-1|k)]T，取第一个元素Δu(k|k)=Δu*(k)。

Step3由Step 2得时刻k的MPC控制量为u(k)=u(k-1)+Δu*(k)并作用于实际系统。

Step4测量系统状态量x(k)，令k=k+1，返回Step 2。

其中，势场函数权重矩阵Q越大，越容易避开障碍物，但相对于速度跟踪项权重矩阵R、控制增量项权重矩阵S和终端惩罚项权重矩阵W，Q较小；R越大，跟踪误差越小；S越大规划的路径越平稳；W越大规划的路径与道路中心线的位置偏差越小。通过试差得到目标函数中的权重参数。

3 仿真与结果分析

仿真中使用的自主车辆与障碍车辆模型均选取CarSim软件中的C级掀背式轿车模型，调用Matlab中求解带约束优化问题得fmincon函数，优化器使用SQP算法，仿真计算机处理器为AMDR5 CPU 2.00 GHz，8 GBRAM和64位Windows 10操作系统。采样时间为50 ms，车辆及控制器参数，纵向加速度及其变化率、前轮转角及其变化率和质心侧偏角的上下界等[16,27]如表1所示。自动驾驶车辆行车环境动态多变，为了对提出的轨迹规划与跟踪高效控制方法进行验证，选取两种典型的交通场景：前方有静态障碍车辆和前方有低速车辆行驶导致换道到相邻车道。

表1 车辆及控制器参数

3.1 静态障碍车辆

设自主车辆前方50 m处有静态障碍车辆，相邻车道有足够的横向空间可以从障碍车侧面通过。仿真中，预测时域取为15，阶梯因子λ取0.7，结果如图5～8所示。由图5可知：障碍车辆势场将被控车辆引导至车道左侧，而充分大的目标点终端惩罚函数将被控车辆拉回右侧车道，规划的自主车辆行驶路径使车辆在保持其车道的同时避免事故的发生。当被控车辆经过障碍车辆时，障碍车边界与被控车边界之间的最小横向距离约为0.3 m。值得注意的是，仿真中选取自主车辆和障碍车辆车宽均为2 m，而实际车辆车宽1.695 m，实际最小横向距离为0.91 m，足够自主车辆安全避开静态车辆障碍。经过障碍车辆后，道路势场将车辆引导至道路中心线行驶。此外，如图7所示，车辆在完成避障之后能跟踪上目标速度且控制量均在约束范围内。表2给出了不同预测时域下传统MPC策略和笔者采用的MPC的单步平均计算时间和最大计算时间。由表2可知：在不同预测时下笔者高效模型预测算法的平均计算时间和最大计算时间均小于传统MPC。特别地，策略在不同预测时域下的单步平均计算时间均小于仿真中设置的控制周期50 ms，这表明笔者采用的阶梯式方法既能显著降低计算量，又能满足实时控制要求。

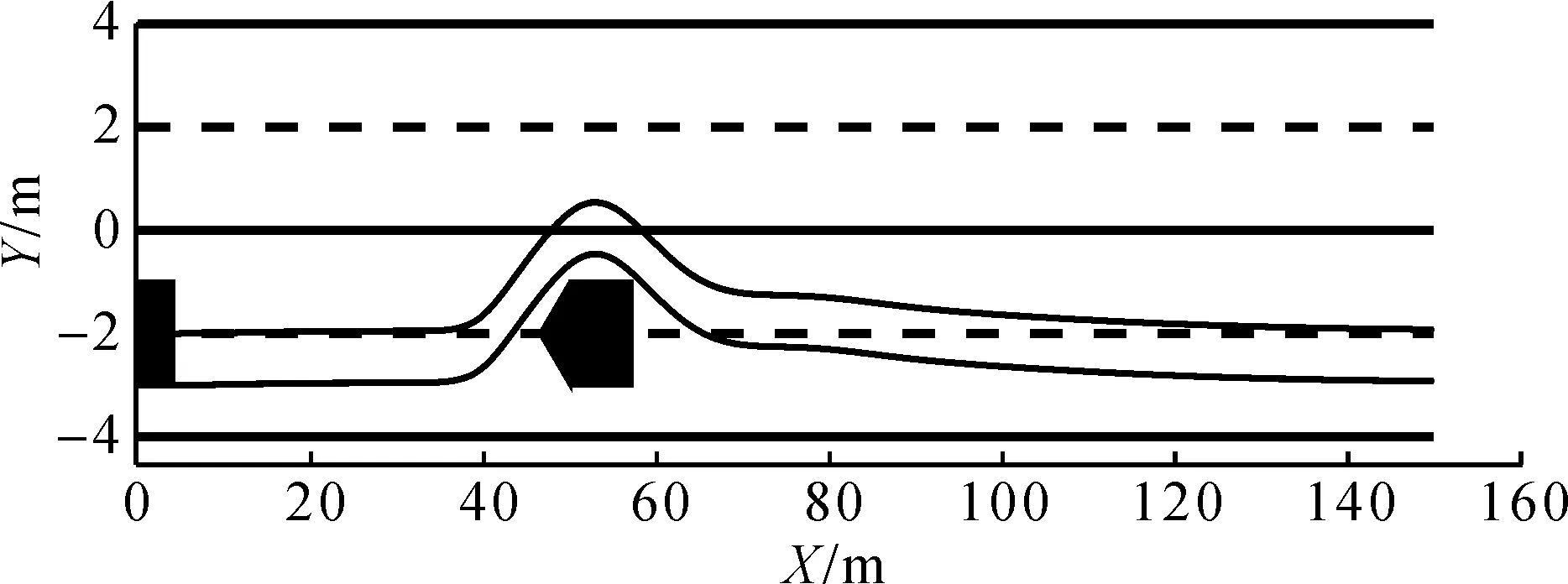
图5 阶梯式MPC规划路径

图6 传统MPC规划路径

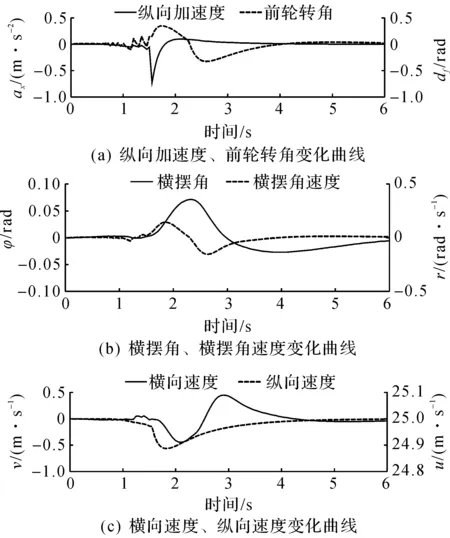
图7 阶梯式MPC控制量及状态曲线

图8 传统MPC控制量及状态曲线

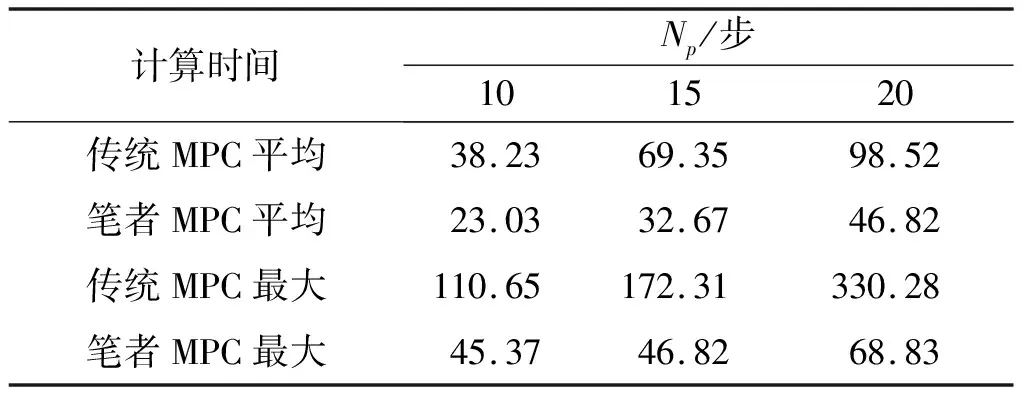
表2 单步平均和最大计算时间

3.2 动态障碍车辆

设自主车辆以25 m/s行驶，前方50 m处有以22 m/s行驶的障碍车辆，相邻车道有换道空间。仿真中，预测时域取为15，阶梯因子λ取0.95，规划路径如图9～12所示。由图9可知：当自主车辆与障碍车辆后方存在一定距离时，障碍车势场引导被控车辆进行换道，同时被控车辆通过调整速度保持与障碍车辆的距离。并且，在换道前后被控车辆始终沿车道中心行驶。由图11可知：控制量变化很小，满足乘坐舒适性要求。同样，表3给出预测时域为10和20的传统MPC与阶梯式MPC单步平均与最大计算时间对比，较大的预测时域虽然能得到更好的轨迹，但计算时间剧增，阶梯式MPC也难满足控制周期约束。图9，10的规划路径都能安全实现换道操作，但笔者方法可以在约39 ms内实现规划和跟踪，相比传统MPC有时需要190 ms才能完成相同的规划与跟踪控制任务更高效。

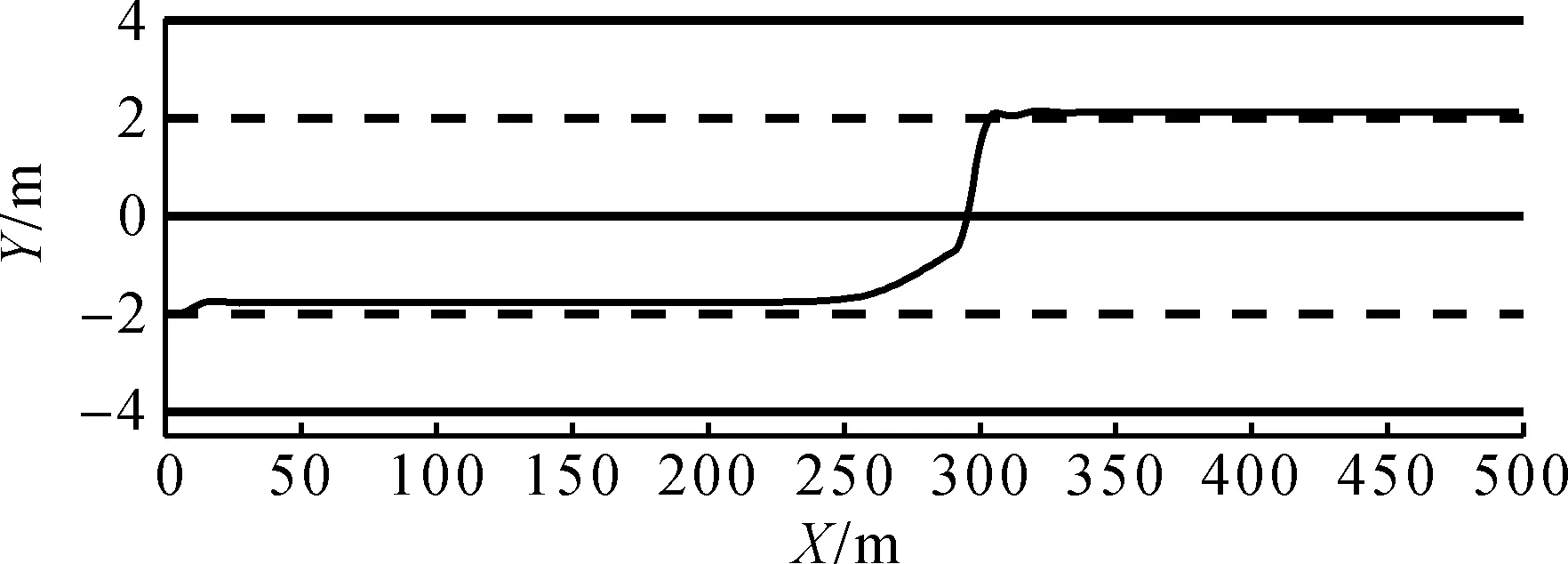
图9 阶梯式MPC规划路径

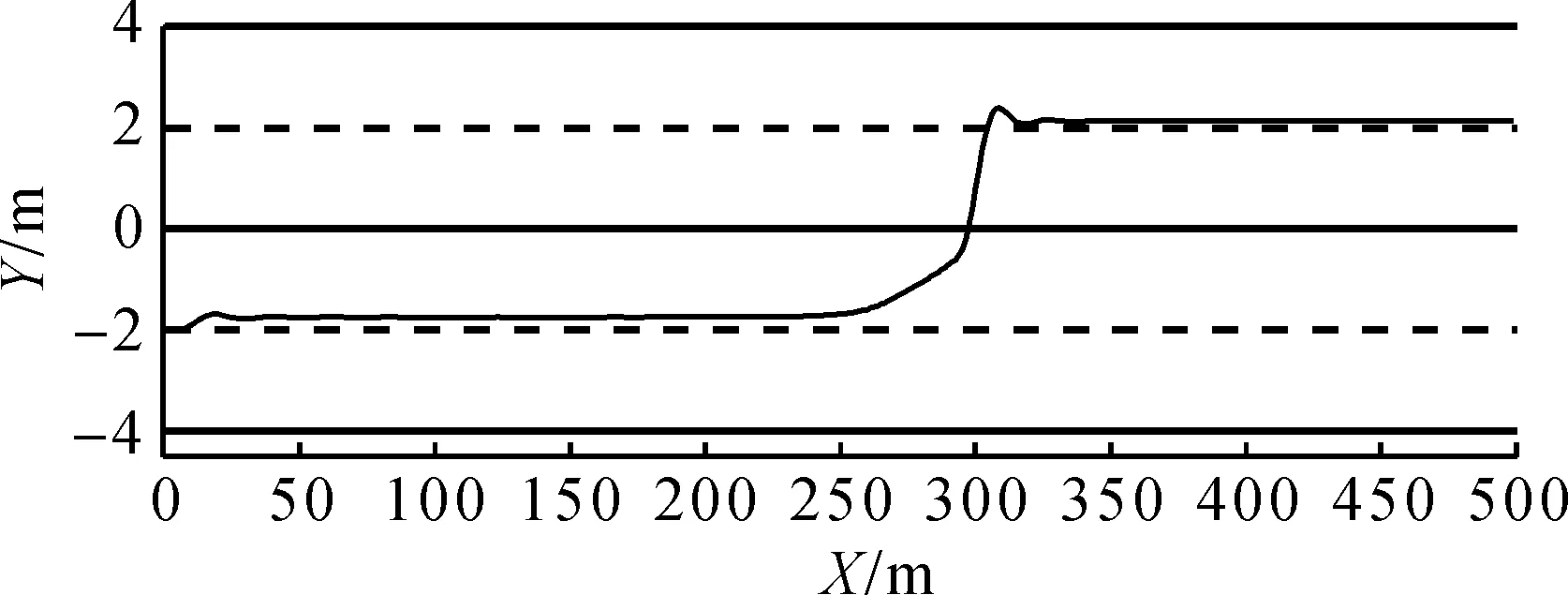
图10 传统MPC规划路径

图11 阶梯MPC控制量及状态曲线

图12 传统MPC控制量及状态曲线

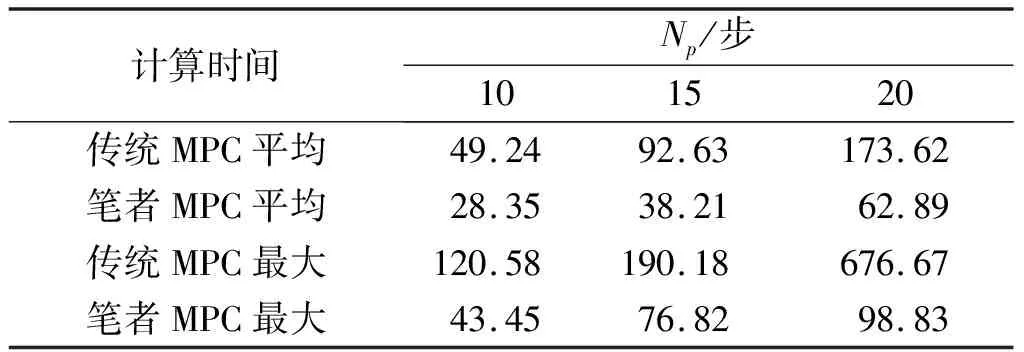
表3 单步平均和最大计算时间

4 结论

提出了一种基于模型预测控制的自主车辆高效滚动时域轨迹规划与跟踪控制方法。采用人工势场法为不同障碍物和道路结构分配不同的势场函数，并将这些表征安全性的势场函数添加到模型预测控制的目标中，以实现轨迹规划。同时采用纵横向耦合的车辆动力学模型作为模型预测控制的预测模型，在自主车辆轨迹规划的过程中可以实现对车辆的纵横向控制。进一步，势场函数的非凸非线性造成模型预测控制性能指标在线优化计算成本高，难以满足系统实时性要求，由此引入阶梯式控制策略，参数化预测时域内的控制增量，来降低模型预测控制在线优化计算量。仿真结果表明该方法有效并具有优越的实时性能。