超大跨度部分地锚式斜拉桥抗震结构体系研究
2021-01-23张新军李博林赵俊杰
张新军,李博林,赵俊杰
(浙江工业大学 土木工程学院,浙江 杭州 310023)
自1956年世界第一座现代斜拉桥——瑞典的斯特洛姆桑特桥建造以后,斜拉桥以其较强的跨越能力和良好的经济性能在400~1 000 m跨径范围得到了广泛的应用。21 世纪以来,苏通长江大桥(1 088 m)、香港昂船洲大桥(1 018 m)和俄罗斯海参威Russky岛大桥(主跨1 104 m)的相继建成实现了斜拉桥主跨超千米的突破。当前,为适应世界桥梁工程的跨海联岛工程建设的需要,斜拉桥的跨径仍将持续增大[1]。当前,大跨度斜拉桥基本都采用斜拉索全自锚体系。全自锚式斜拉桥主跨进入超千米领域后,塔梁交界处主梁承受的过大轴向压力以及由此产生的主梁屈曲问题,已成为限制斜拉桥跨径进一步增大的关键问题[1]。为解决塔梁交接处主梁轴压过大问题,丹麦Gimsing等[2]和法国Muller[3]相继提出了部分地锚式斜拉桥结构体系,该体系将边跨部分斜拉索集中锚固于地锚上,中跨跨中部分区段采用缆索吊装施工,该部分斜拉索索力水平分力转化为主梁中的拉力,从而有效地缓解了塔梁交接处主梁承受的巨大轴向压力。已有研究表明:部分地锚斜拉桥的结构设计和施工都是可行的,较之于相同主跨全自锚式斜拉桥具有主梁压力减小、稳定性提高和结构刚度增大等优点[4]。部分地锚式斜拉桥比自锚式斜拉桥跨越能力强,且锚碇规模一般比悬索桥要小很多,对地质条件的要求较悬索桥低。在自锚式斜拉桥跨径受限而地质条件适宜修建锚碇的情况下,部分地锚式斜拉桥体系在1 100~1 600 m跨径范围内可以与自锚式斜拉桥及悬索桥竞争。
近年来,国内外学者对部分地锚斜拉桥的结构体系[4-5]、静力性能[6-9]、经济性能[10]、动力特性[11]以及抗风性能[12]等方面开展了大量的研究工作,但对重要的结构抗震问题基本未涉及。众所周知:大跨度部分地锚式斜拉桥是一种柔性结构体系,水平刚度小,地震作用下的结构性能是其设计需要考虑的重要因素。为此,笔者以一主跨1 400 m的部分地锚式斜拉桥设计方案为背景,采用反应谱法进行E1地震作用下的结构地震反应分析,揭示其抗震性能特点。在此基础上分析地锚段主梁长度、主梁宽度、主梁高度、桥塔高跨比、地锚索倾角、辅助墩数量和塔梁连接方式等主要结构设计参数对部分地锚式斜拉桥结构地震反应的影响,结合结构静力性能和稳定性探讨其合理取值以及适宜的抗震结构体系。
1 主跨1 400 m部分地锚式斜拉桥设计方案简介
图1为主跨1 400 m的部分地锚式斜拉桥设计方案[13],采用全漂浮体系,桥跨布置为144 m+300 m+1 400 m+300 m+144 m,边主跨径比为0.317,两侧边跨内距离边墩144 m处各设置一个辅助墩;中跨自锚梁段长度1 000 m,跨中400 m长度的梁段通过边跨拉索锚固在地锚上;主梁为高4.5 m和宽41 m的扁平钢箱梁,跨高比为311,跨宽比为34.1,宽高比为9.1;桥塔为A型桥塔,采用钢筋混凝土结构,塔高357 m,其中桥面以上高度为287 m,高跨比为0.205。桥塔分别在塔梁连接处设置下横梁,并在拉索锚索区下端设置上横梁;斜拉索采用空间倾斜扇形双索面布置,共计304 根(38×2×4),其中两侧边跨共计52(13×4)根斜拉索锚于地锚上。

图1 主跨1 400 m部分地锚式斜拉桥立面布置图(单位:m)
2 结构三维有限元建模
采用Midas/Civil有限元分析软件,建立了如图2所示的结构三维有限元模型,共计663 个节点和932 个单元,主梁、桥塔和横梁采用空间梁单元模拟,斜拉索则采用空间桁架单元模拟,桥面主梁采用鱼骨式计算模型,斜拉索与主梁之间连接采用刚臂单元模拟。结构模型约束信息:主梁纵向漂浮,主梁与边墩和辅助墩之间的横桥向、竖向和绕纵轴等3 个方向自由度保持从属关系,沿桥纵向位移、绕横轴和竖轴转动自由;主梁与桥塔下横梁之间只有竖向约束,其它方向位移自由;桥塔底部和地锚处均按固结处理。
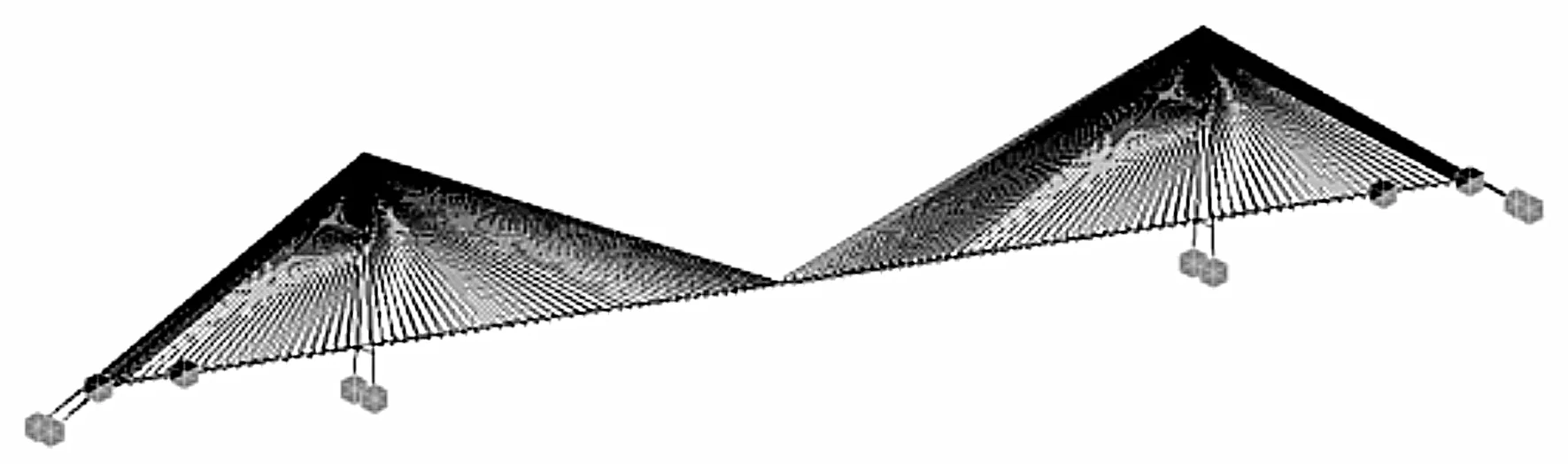
图2 结构三维有限元分析模型
采用Midas/Civil有限元分析软件的“未知荷载系数”功能和调索工具对该桥成桥状态的斜拉索初始索力进行分析,在此基础上考虑斜拉索初始索力、结构自重和二期恒载的共同作用,通过结构三维几何非线性有限元分析计算出成桥状态结构的几何和内力状态,以此作为后续地震反应分析的基准态。
3 大跨度部分地锚式斜拉桥结构地震反应分析
3.1 地震动输入
设计方案桥为A类桥梁,桥址处抗震设防烈度为7 度;水平向设计基本地震动加速度峰值为0.10g;场地类型为Ⅲ类,场地土特征周期为0.55 s;结构阻尼比为3%。根据《公路桥梁抗震细则》(JTG/T B02-01—2008)[14]确定分析采用的地震动反应谱,E1地震作用的水平设计加速度反应谱如图3(a)所示,竖向地震动加速度反应谱取为相应水平设计加速度反应谱的1/2,如图3(b)所示。

图3 E1地震作用的水平和竖向设计加速度反应谱
3.2 结构地震反应分析
基于MIDAS/Civil有限元分析软件,在E1地震作用下,采用多振型地震反应谱分析方法,考虑结构前230 阶振型参与,对该设计方案桥分别进行纵向、横向和竖向地震作用的结构地震反应分析。由结构动力特性分析发现该桥自振频率分布密集,振型间藕合效应显著,因此各振型的地震反应采用CQC方法组合。限于篇幅,在此仅给出桥塔和主梁的地震反应峰值,如表1所示。

表1 E1地震作用下结构地震反应峰值
结合结构地震反应包络图和表1的结构地震反应峰值进行综合分析,超大跨度部分地锚式斜拉桥的地震反应具有以下特点:
1)纵向地震作用下,桥塔顺桥向振动,主梁则表现为顺桥向和竖向耦合振动。桥塔塔顶处的纵向位移最大,并在塔底截面产生最大纵桥向弯矩、剪力和轴力;主梁沿桥轴向的纵向位移基本一致,并在中跨跨中附近产生最大竖向位移。主梁的最大竖向弯矩和剪力均出现在边跨辅助墩处,其次为中跨跨中处。与主梁相比,纵向地震作用下桥塔受力更加显著,并应特别重视塔底截面的抗震设计。
2)横向地震作用下,桥塔和主梁同时产生横桥向振动。桥塔最大位移发生在桥塔上横梁附近,最大横向弯矩出现在塔梁连接处,最大横向剪力和轴力则出现在塔底。主梁最大横向位移出现在中跨跨中;最大横向弯矩发生在塔梁连接处,中跨跨中横向弯矩次之;最大横向剪力发生在边跨辅助墩附近,塔梁连接处次之。与纵向地震作用相比,桥塔和主梁的横向地震反应更为显著,横向地震作用对结构受力更为不利,同时应特别重视塔梁交接处桥塔塔柱和主梁截面的抗震设计。
3)竖向地震作用下,桥塔和主梁的振动形式与纵向地震作用基本相同。桥塔最大纵向位移出现在塔顶处,最大纵向弯矩、剪力和轴力都出现在塔底;主梁最大竖向位移出现在中跨跨中;最大竖向弯矩出现在辅助墩附近,中跨跨中次之;最大剪力也出现在辅助墩附近,最大轴力则出现在跨中。
4)纵向和横向地震作用下结构的地震反应均显著大于竖向地震作用,因此应重视水平地震作用下超大跨度部分地锚式斜拉桥的抗震性能。同时,在纵向、横向和竖向地震综合作用下,桥塔的塔底和塔梁交接处、主梁的塔梁交接处和边跨辅助墩处的地震反应均非常大,应特别重视这些截面的抗震设计。
4 超大跨度部分地锚式斜拉桥地震反应的结构设计参数分析
为探明大跨度部分地锚式斜拉桥适宜的抗震结构体系,以上述设计方案桥为原型,通过改变地锚段主梁长度、主梁宽度、主梁高度、主塔高跨比、斜拉索的倾斜角度、辅助墩的数量和塔梁的连接方式等主要结构设计参数建立对比方案桥,通过地震反应的分析和比较提出关键的设计参数及其合理取值。规范指出:若同时考虑顺桥向、横桥向和竖向地震作用时,可分别单独计算各方向地震作用产生的最大效应,总的最大地震作用效应取为各方向最大地震效应平方和的平方根[14]。限于篇幅,以下表格中的各项位移和内力值均采用规范方法计算得到的组合值。
4.1 地锚段主梁长度
地锚段主梁指的是部分地锚式斜拉桥中与地锚索所对应的中跨主梁段,该主梁段长度变化会影响整个桥梁的刚度,是该体系斜拉桥的一个重要结构设计参数。斜拉桥地锚段主梁长度取决于地锚索数量占所有斜拉索数量的比重,以上述部分地锚式斜拉桥方案桥为原型,保持主跨长度不变,通过调整地锚索数量来改变地锚段主梁长度,同时对边跨长度进行相应的调整,且均不设置边跨辅助墩以求消除辅助墩数量和位置改变对结构抗震性能影响。通过主跨为1 400 m的部分地锚式斜拉桥静力性能研究发现,当地锚段长度在400 m附近时其整体刚度表现良好,因此分别取地锚段主梁长度为272,400,528 m等进行对比分析,相应的地锚段主梁长度与主跨长度比值为0.19~0.38,不同地锚段主梁长度的对比方案桥情况见表2,地锚段主梁长度对结构地震反应的影响见表3。

表2 不同地锚段主梁长度的结构参数
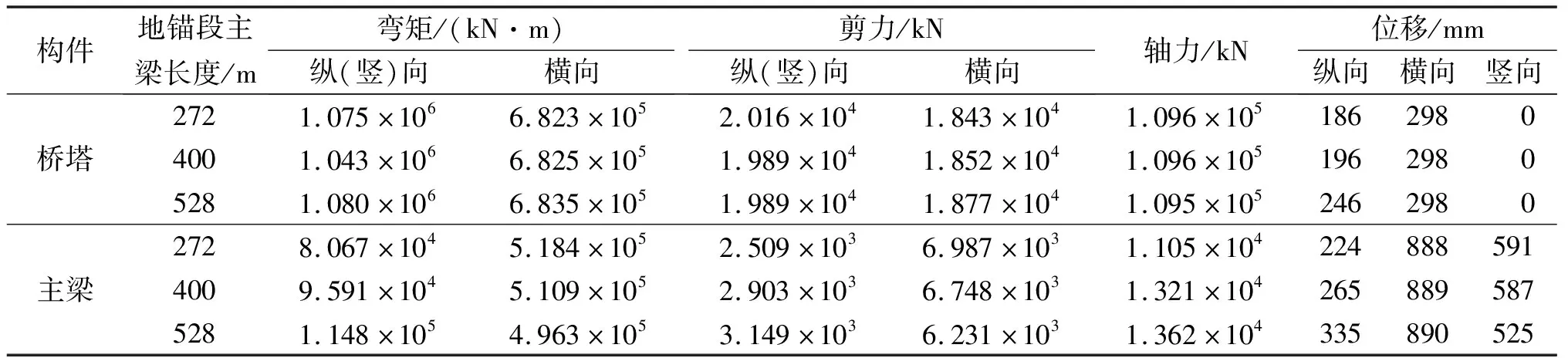
表3 地锚段主梁长度对结构地震反应影响
由表3可知:地锚段主梁长度的改变对桥塔的纵向地震反应和主梁的竖向地震反应影响比较显著,而对其横向地震反应影响很小。随着地锚段主梁长度增大,主塔在地震作用下纵向位移明显增大,同时牵引着主梁产生较大的纵向位移,而且随着地锚索竖向支承刚度的增强,主梁的竖向位移则明显减小;桥塔的纵向弯矩有所增加,主梁的竖向弯矩和剪力及轴力则明显增大。因此,从抗震性能角度而言,地锚段主梁长度不宜太大。结构静力特性和稳定性分析建议地锚段主梁长度的合理范围取为400~800 m,尤以400~600 m为优[13]。结合结构静力性能,地锚段长度和主跨长度之比在0.3左右时,部分地锚式斜拉桥结构整体受力性能较好。
4.2 主梁宽度
桥面主梁宽度主要由设计交通量决定,但主梁宽度直接影响到主梁的侧向刚度,同时对风和地震等水平力作用下结构的受力性能和稳定性产生重要影响。考虑结构空气动力稳定性,《公路斜拉桥设计细则》规定桥宽与跨径之比不小于1/30,桥宽与梁高之比不小于8[15]。以设计方案桥主梁为原型,在改变主梁宽度的同时保持截面竖向弯曲惯性矩和截面面积不变,仅改变主梁扭转惯性矩和侧向弯曲惯性矩,分析主梁宽度变化对结构抗震性能的影响。主梁宽度在设计方案桥的基础上分别增减3.75,7.5 m,相应的主梁断面几何特性值如表4所示,主梁宽度变化对结构地震反应的影响见表5。

表4 不同主梁宽度的截面几何特性值

表5 主梁宽度对结构地震反应影响
从表5可知:主梁宽度变化对结构横向地震反应影响显著,对竖向和纵向地震反应基本没有影响。同时,主梁宽度变化对桥塔地震反应影响很小,但主梁的地震反应影响显著。由表4可知:随着主梁宽度的增大,主梁的侧弯刚度明显增大,由于截面积不变致使主梁所受的地震惯性力没有变化,主梁的横向地震位移因而显著减小,但其横向弯矩和剪力却随之明显增大。因此,随着主梁宽度的增加,结构的横向抗震性能有所提高。结构的静力特性和稳定性研究也表明在相同材料用量前提下采用较宽主梁对结构较为有利[13]。因此,较宽的主梁对结构总体受力性能比较有利,但主梁宽度选取还是主要考虑交通量和结构空气动力稳定性要求。
4.3 主梁高度
主梁高度变化会直接影响主梁的竖向刚度以及主梁的面内受力性能。《公路斜拉桥设计细则》规定:双塔三跨斜拉桥钢主梁高度与主跨跨径比值宜为1/180~1/330[15]。与主梁宽度变化相似,在改变主梁高度的同时保持侧向弯曲惯性矩和截面面积不变,仅改变主梁竖向弯曲惯性矩和扭转惯性矩,从而在相似的成桥状态下分析主梁高度对结构抗震性能的影响。主梁高度在设计方案桥的基础上分别增减0.5,1.0 m,相应的主梁截面几何特性值见表6,主梁高度对结构抗震性能的影响如表7所示。

表6 不同主梁高度的截面几何特性

表7 主梁高度对结构地震反应影响
由于主梁截面的侧向弯曲惯性矩和截面积保持不变,主梁的面外刚度和自重以及所受的地震惯性力均不变,因此主梁和桥塔的横桥向地震反应基本不随主梁高度的改变而变化。同时,桥塔的纵桥向地震反应受主梁高度的影响也非常小。主梁高度的改变主要影响主梁的纵桥向和竖向地震反应。随着主梁高度增大,如表6所示主梁的竖向刚度明显增强,主梁的竖向弯矩和竖向位移因而明显减小,但纵桥向位移有所增大。因此,增加主梁高度可以提高结构的抗震性能。结构静力特性和稳定性研究表明梁高改变对结构总体刚度影响较小,却对极限静侧风响应很不利,因此在保证局部刚度和整体抗风稳定性前提下宜采用较小梁高[13]。因此,主梁最优高度需要结构静力性能和稳定性要求综合确定。
4.4 桥塔高跨比
桥塔高跨比指的是桥面以上桥塔高度与主跨跨径之比,主塔高度改变后直接改变了结构总体外形,对结构刚度、受力特性等有直接影响。《公路斜拉桥设计细则》规定:双塔斜拉桥桥塔高跨比宜为1/4~1/6[15]。在设计方案桥的350 m桥塔总高度基础上,通过改变方案桥主塔上下横梁间的塔柱高度对塔高分别增减25 m和50 m建立对比方案桥,相应的桥塔高跨比为0.169~0.241,外索拉索倾角为18.7°~25.7°,分析桥塔高跨比对结构抗震性能的影响,结果如表8所示。

表8 桥塔高跨比对结构地震反应影响
从表8可以看出:桥塔高度对桥塔的纵横向地震反应以及主梁的纵向和竖向地震反应影响非常显著,但对主梁的横向地震反应影响较小。桥塔地震作用下的纵横向位移和纵向弯矩随着桥塔高跨比增大而明显增大,横向弯矩和纵向剪力随桥塔高跨比增大而减小,横向剪力在主塔高跨比为0.205时最小。主梁在地震作用下,除了横向剪力外所有内力都随桥塔高跨比的增加而增大,横向剪力在高跨比为0.187时最小,纵向位移随着桥塔高跨比增大而增大,竖向位移则随桥塔高跨比增大而减小。同时发现,桥塔和主梁的地震反应在桥塔高跨比超过0.205后呈现出跳跃式的显著增大趋势。总体上看,增加桥塔高度对部分地锚式斜拉桥的抗震性能不利,综合结构的静力性能和经济性,桥塔高跨比宜取0.2左右。
4.5 地锚索倾角
地锚索倾角是指边锚索与水平面形成的夹角,它随着地锚位置的改变而变化。部分地锚斜拉桥中地锚拉索的受力特性、作用、锚固构造等均与悬索桥的边跨主缆类似,因此拉索倾角也参照悬索桥常用数值,变化范围取为21.4°~34.2°。《公路斜拉桥设计细则》规定:斜拉桥端锚索的水平倾角不宜小于22°[15]。设计方案桥的地锚索倾角为32°,通过平移地锚的位置来改变地锚索的倾角,其余条件保持不变,建立地锚索倾角分别为28°和30°两个对比方案桥进行结构地震反应分析,地锚索倾角改变对结构地震反应的影响如表9所示。

表9 地锚索倾角对结构地震反应影响
从表9可以看出:地锚索倾角的改变对桥塔和主梁的地震反应影响不明显,是一个不敏感设计参数。总体上看,地锚索倾角的增大可以减小桥塔和主梁的纵向地震位移及其内力,对结构抗震性能有利。因此,在地形地质和经济性等条件允许的情况下,尽可能选择较大的地锚索倾角。
4.6 辅助墩数量
辅助墩的主要作用表现为施工中加强结构的稳定性及增强成桥结构的刚度,但其数量受到边孔通航要求、施工期安全以及经济性等条件的约束。根据主跨为1 400 m部分地锚式斜拉桥的静力分析可知,当辅助墩超过2个时,再增加辅助墩对桥梁整体刚度影响不大[13]。设计方案桥边跨内设辅助墩一个,保持边跨长度不变,在此基础上分别增减辅助墩数量1个,形成如表10所示的对比方案并进行地震反应分析,辅助墩设置数量对部分地锚式斜拉桥结构地震反应的影响见表11。

表10 不同辅助墩设置数量的边跨布置情况

表11 辅助墩数量对结构地震反应影响
在设计方案桥基础上再增设1 个辅助墩时,桥塔的地震反应变化很小;主梁的横向和竖向位移都明显减小,主梁竖向和横向的弯矩和剪力也随之减小,结构整体抗震性能因而有所提高。反过来,若边跨不设辅助墩,桥塔的纵横向和主梁的竖横向地震反应都有所增大,结构抗震性能减弱。因此,边跨设置辅助墩可以增强结构的抗震性能,结合结构静力性能,边跨宜设置1~2个辅助墩。
4.7 塔梁连接方式
斜拉桥常见的塔梁连接方式有漂浮、半漂浮、固结、塔梁固结塔墩分离等4 种,《公路斜拉桥设计细则》规定对于跨度较大、索距较密的斜拉桥宜选择漂浮体系或半漂浮体系[15]。设计方案桥采用的是全漂浮体系,在设计方案桥基础上,增加主梁在桥塔部位的竖向支撑建立半漂浮体系的对比方案桥,并对其地震反应进行分析,塔梁连接方式对部分地锚式斜拉桥结构地震反应的影响如表12所示。

表12 塔梁连接方式对结构地震反应影响
从表12可以看出:塔梁连接方式的改变对结构的地震反应基本没有影响。从静力分析可知:斜拉桥采用半漂浮体系时塔梁结合处主梁的负弯矩很大,同时增加桥塔下塔柱和支承横梁的受力。因此,综合静力和抗震性能,部分地锚式斜拉桥宜采用全漂浮体系。
5 结 论
以1 400 m主跨的部分地锚式斜拉桥设计方案为背景,采用多振型地震反应谱分析方法,分析了地锚段主梁长度、主梁宽度、主梁高度、桥塔高跨比、地锚索倾角、辅助墩数量和塔梁连接方式等主要结构设计参数对结构地震反应的影响,并结合结构静力性能和稳定性提出了适宜的结构布置形式。研究结果表明:大跨度部分地锚式斜拉桥当地锚段主梁长度和主跨之比约为0.3,采用较宽的主梁并增大其高度,桥塔高跨比约为0.2,采用较大的地锚索倾角,边跨设置1~2 个辅助墩以及采用全漂浮体系时,结构整体性能良好。
