高中“概率与统计”习题设置研究
2021-01-22孙露柴小雨
孙露 柴小雨

【摘要】本文笔者基于统计的情境性以及数据分析素养的内涵,从情境类型和数据分析两个视角对高中数学教材中“概率与统计”部分习题的设置进行统计与分析,依据分析结果提出适当增加科学情境和职业情境类题目以及增加收集数据类、整理和分析数据类题型的比例等教材优化方案与编写建议.
【关键词】高中;概率与统计;习题;情境;数据分析
【基金项目】安徽省教育科学研究项目“基于核心素养下高中生数据分析水平现状及其培养研究”(JK19049)的阶段性成果.
习题训练作为学生学习过程中必不可少的重要环节,有助于加深学生对数学知识的理解,帮助学生形成良好的数感和科学的思维模式,是增强学生数学思维的具体形式与提升数学能力的有效途径.通过习题训练能够有效提高学生的综合素质.“概率与统计”作为发展学生的数据分析核心素养的主要内容,随着信息时代的发展,扮演着越来越重要的角色.“数据分析”作为数学六大核心素养之一,“是指针对研究对象获取数据,运用数学方法对数据进行整理、分析和推断”[1],主要通过“概率与统计”这一部分内容的学习逐步养成.因此,为了多方面提高学生的各项能力,应对教科书中的习题进行有效的选择与设计,并且结合“概率与统计”在高中数学中的地位,对教科书中相关习题的设置进行整理与分析.
一、高中“概率与统计”习题的教学功能
依据“概率与统计”内容的难度以及基本学习要求,分别在高中必修和选修课程中设置了相应的学习内容.同时依据学生未来专业发展的需要,文科与理科的学习要求和侧重点也不同.在人教A版必修3中,设计了概率初步和统计初步的内容,在选修1-2和选修2-3中设计了统计案例,在选修2-3中设计了对概率中随机变量和一些离散变量的随机模型的学习,“概率与统计”内容的教学课时也有所增加,充分凸显出了“概率与统计”在高中数学中的地位.
习题作为高中数学学习的重要组成部分之一,是学生认识问题、理解问题、解决问题的钥匙,对提高学生思考和探究问题的能力有积极意义.“概率与统计”部分的例题及课后习题则围绕数据分析这一核心素养,有助于学生在问题的分析与解决过程中形成用理论、用数据说话的意识、习惯.具体来说,有以下两个方面:
首先,“概率与统计”部分的例题与习题具有指导作用,这一部分的习题大多与我们的实际生活相关,可以让学生更容易进入教学情境,激发了学生解决问题的兴趣,引起了学生对知识的渴望,促进了他们数学思维的养成.
其次,基于统计的全过程特征,学生在相关习题的解决过程中不仅能经历数据收集、分析、处理的全过程,还学会将实际问题转化为统计模型,积累统计问题的解决经验,在锻炼其基本思维能力的同时有助于他们感受统计的实用性.
二、高中“概率与统计”习题基本情况
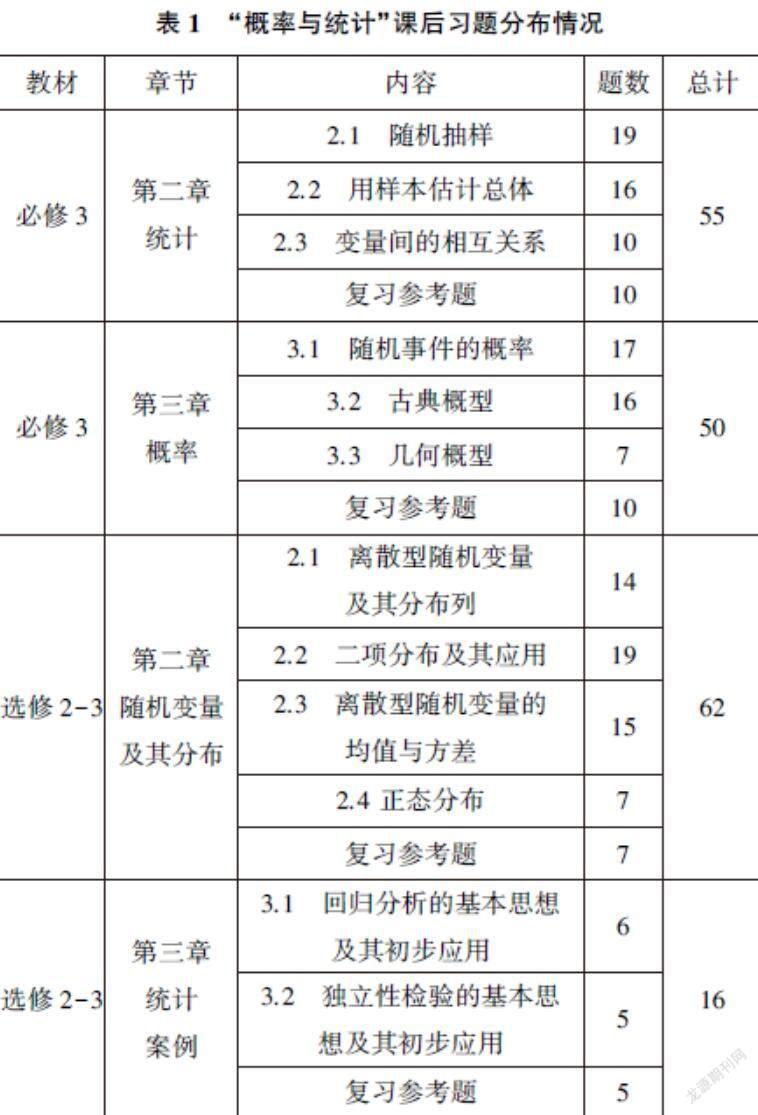
选取被广泛使用的人教A版教材对其中的“概率与统计”习题设置进行研究.同时考虑到文理类学生的学习要求不同,选取了高中学生共同学习的必修3及选修系列2-3中所含有的统计知识及其习题.
由表1可以看出必修3中的第二章、第三章以及选修2-3中的第二章的习题数相差不多,分别为55,50,62题,选修2-3第三章的习题数略显单薄,但从总体来看,各章节习题量的设置较为合理、均匀.
三、习题类型的統计分析
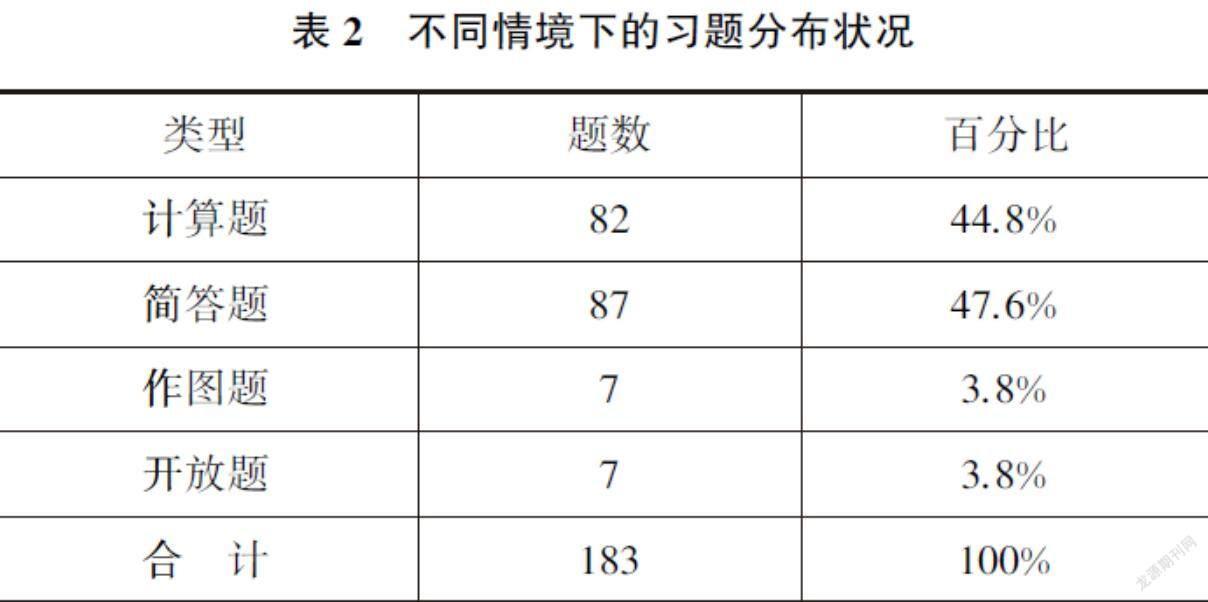
基于习题的分类以及“概率与统计”部分在教材中所出现的题型,可将其主要分为:计算题、简答题、作图题、开放题.具体的习题类型统计情况如表2:
通过表2可以很清楚地看出习题的类型主要集中在计算题和简答题上,其中计算题的占44.8%,简答题的占47.6%.相对传统的封闭题而言,教科书在开放题这一类型的设置上则较少,仅占3.8%.梳理发现,计算题主要围绕数据的分析和概率初步这些涉及所学的概念和公式的部分,较多集中在概率这一部分,需要学生将基础的概念和公式掌握牢固,且能用灵活运用;简答题则主要考查学生对新知识的运用和理解,要求学生能在解决问题后分析出“为什么”,题目难度相对较高,主要目的是通过题目来培养学生的数据分析能力.
四、习题情境的统计分析
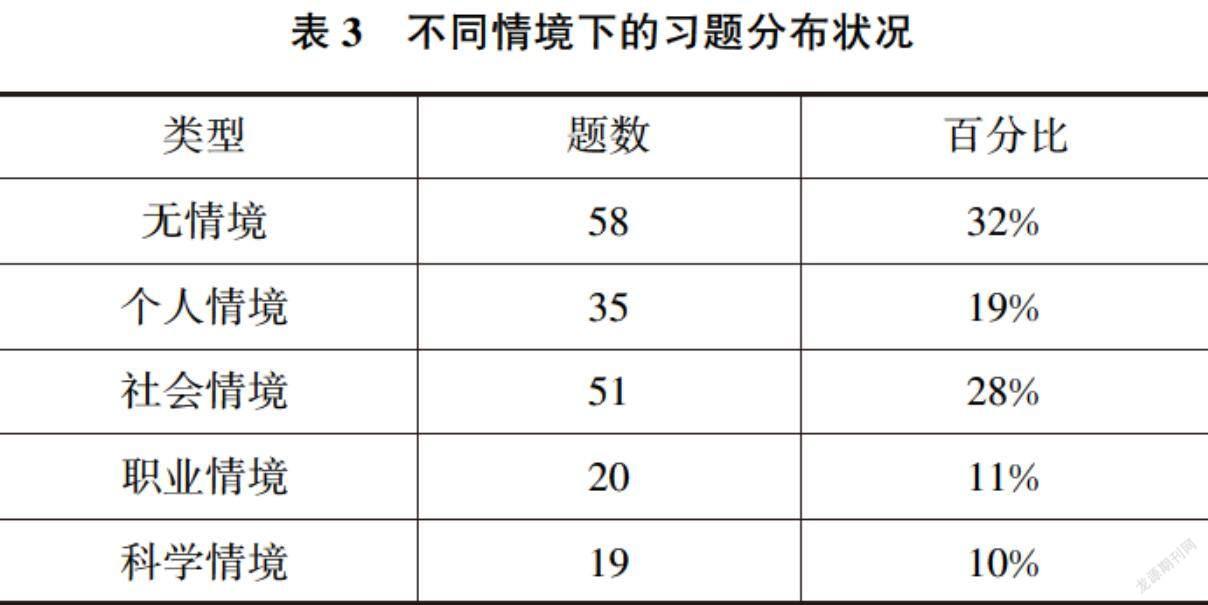
数据作为“概率与统计”的主要研究对象,情境性是其主要特征,且情境是产生数学概念、发现数学问题、提出和解决数学问题的背景、前提、条件和基础.因而选取PISA对于情境类型的划分,将所考察的“概率与统计”习题分别按照无情境、个人情境、社会情境、职业情境、科学情境五种情境进行分类统计.
表3数据表明,“概率与统计”的情境类型分布有较大差异.在183道课后习题中,无情境的习题出现最多,所占百分比约为32%;随后为社会情境类习题,所占比例在28%左右;排在第三的为个人情境类习题,占比约为19%;而职业情境类和科学情境类习题所占比例最低,分别约为11%和10%.
五、数据分析内涵的统计分析
“数据分析”作为数学核心素养的一个重要内容,也是统计的核心所在.《普通高中数学课程标准(2017年版)》对其的内涵解读主要包括收集数据、整理和分析数据、推断和评价三方面.其内涵分别为:
(1)收据数据:对有价值的问题采用多种收集数据的方法,并结合具体问题选择合适的抽样方法;
(2)整理和分析数据:可以运用合适的统计图,求出相应的统计量,直观认识变量间的相关关系;
(3)推断和评价:运用统计的基本方法和思想解决实际问题,体会“随机性”与学生习惯性的确定思维的不同,对数据处理过程做出评价.
结合以上三方面内涵对相关习题进行整理与统计(见表4).
由表1的“概率与统计”习题的分布情况可以看出,必修3的第二章和选修2-3的第三章主要涉及统计知识,其他两章主要为概率内容,在运用数据分析素养进行习题设置统计时也发现,必修3的第二章和选修2-3的第三章中更多涉及收集数据、整理数据和分析数据类型的习题,如必修3第二章的第一节内容就是抽样方法,这一节的习题基本都是选择不同的抽样方法收集数据;必修3第二章的第二节基本上都是对数据的整理与分析.从总体来看,概率部分的内容属于运用统计方法与思想解决问题,即推断和评价类,总题数达到114题,占比约为62.3%.收集数据是分析数据的前提.选择合适的抽样方法,并筛选数据,整理数据,分析数据采用恰当的统计图,更直观地反映变量间的相关关系,这样才能提升学生的数据分析素养,但教材中的收集数据与整理分析数据类习题数相对较少,占比仅为16.4%和21.3%,且习题的知识点综合程度较低,基本上是“就知识点论知识点”,在概率章节,收集数据等题型很少出现.
六、建议与思考
(一)均衡习题情境类型
统计结果反映出高中“概率与统计”习题主要是围绕社会情境和个人情境进行设计的.主要有以下两方面原因:首先从学情来看,处于青春期的高中生对新鲜事物充满好奇,当习题设置的情境能够迎合学生的兴趣、抓住学生的眼球时,学生才愿意去接受习题中所包含的信息.教师可以结合学生熟悉的个人情境、社会情境,有效沟通数学与学生生活间的联系,提升学生学习数学知识的兴趣.其次,“概率与统计”从具体情境中来,也将具体运用在现实情境中,优秀的习题是从生产、生活中选取得到的,利用这些熟悉的情境可以让学生消除陌生感,从而合理地通过已有现实经验来理解数学知识与方法.
但数据表明,教科书中有关科学情境的习题占比较少.数学作为自然科学重要的一部分,在高中其他学科课程的学习中时常会用到,因而可以借鉴其他国家数学教材的经验将其他学科内容有效融入数学习题之中,使各个领域的知识相互启发、互为补充.例如,必修3中“2.3变量间的相互关系”一节中以某种身体可以吸收汞的鱼为研究对象的习题.该题将化学知识作为情境融入习题中,既让学生认识到变量间的相互关系,也让学生意识到科学与生活的息息相关,认识到汞元素的危害性,知道当出售的鱼中若含有超量的汞,则不利于人们的身体健康.同时,对职业情境类的习题整理后发现,题量占比不仅较少且职业类型较为单一,主要以零件加工、成本计算等呈现.虽然对于高中生来说,离工作还有一段距离,但是提前在数学学习中了解职业情境更有利于学生的思想成熟,让学生体会到数学知识在以后工作中的应用,可以提高数学学习的目的性.
因此,高中数学教材“概率与统计”部分的习题可以进行适当修改,适当增加科学情境和职业情境类题目,在从学生实际知识需求出发的同时注意情境设置的多元化,让学生在习题练习中感知数学的广泛应用性.
(二)凸显统计的过程性
史宁中教授认为培养学生的数據分析观念需要让学生了解数据获得、分析、处理以及做出决策的全过程,让其在过程体验中领悟数据分析的无穷魅力,从而提高数据分析素养.但统计结果表明,收集数据类以及整理和分析数据类题目均相对较少,占比只有16.4%和21.3%.
“概率与统计”不能仅仅局限于公式和计算,要让学生理解统计的动因,掌握统计的具体步骤,分析统计结果,并评价统计的意义.学生只有亲身参与统计的整个过程,才能深刻理解统计的意义.学生从小接受的数学知识甚至其他学科知识大多数都是确定性的,主要依靠单纯记忆和套用公式机械计算,推断与评价类题型的练习可以让学生感受确定性与不确定性的差异,锻炼活跃的思维,提升“数据分析”核心素养.例如,选修2-3“3.1回归分析的基本思想及其初步应用”中有涉及我国1993~2002年国内生产总值数据的习题,就有效地融入了社会情境.但数据相对陈旧,因此教师可以进一步增加学生收集数据的环节或者在原有数据的基础上组织学生将统计年份适当加长,让学生了解GDP的统计方式以及数据的来源,并在收集整理数据的同时使其切实体会到我国近年来的社会经济变化,感受到国家GDP的变化趋势,感知国家综合实力的增强,搭建学生与社会亲密接触的平台.这样不仅有助于学生提高社会意识,还能让学生认识到数据统计对社会的重要性.
(三)加强习题的开放性
数据分析是有目的性的活动,人们进行数据分析是为了通过它来解决某些实际问题.习题是用来发展学生的数据分析观念的,因此习题的类型与数目设置需合理.教科书在“概率与统计”这一内容的不同类型习题数量设置上有着明显的差异,计算题、简答题相对较多,而侧重思维发散的开放性问题则少有涉及.因而,在“概率与统计”部分习题设置上建议可减少机械的同类型问题训练,在给学生减负的同时使得题目更具代表性,另外,还要多增加开放题的设计,结合开放题的特征——条件不完整或是结论不封闭,鼓励学生用自己的方式去收集、分析数据,加强学生的创新意识.例如,教师可以结合大家日常熟悉的温度变化以及秋游等生活情境,鼓励学生利用各种方式收集未来一周的气温数据,并依据所收集数据对秋游活动的日期安排以及服装选择等实际问题做出决策.这一开放性问题不仅要求学生将一系列的现实生活中的数据转化为数学信息,还要求学生能够用数学思维去思考一些超出数学课本知识的问题,运用数学知识去解决实际问题,要有能将知识整合在一起并分析的能力.在此过程中,学生需要基于网络收集数据,合理选择合适的表示数据的方式,发现数据蕴含的规律并预测某一时段的气温,增强了自身分析数据、灵活解决问题的能力.
因此,在教材编写时可以适当增加收集数据类题目,提高整理和分析数据类题型的比例,让学生通过自主探究,通过收集、处理数据,养成独立思考与分析问题的好习惯,在体会“随机性”的同时提升数学核心素养.
【参考文献】
[1] 陈晓,周仕荣.从“概率与统计”考点看高考中的“数据分析”学科核心素养:以2016-2017两年高考理科数学全国卷为例[J].数学通报,2018,57(08):44-47.
[2] 朱琛,唐恒钧,徐元根.中澳初中数学教科书习题情境的比较分析:以“统计与概率”领域为例[J].现代中小学教育,2018,34(01):91-95.
[3] 胡典顺,雷沛瑶,刘婷.数学核心素养的测评:基于PISA测评框架与试题设计的视角[J].教育测量与评价,2018(10):40-46,64.
[4]人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心.普通高中课程标准实验教科书·数学必修3[M].北京:人民教育出版社,2012.
[5]人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心.普通高中课程标准实验教科书·数学选修2-3[M].北京:人民教育出版社,2007.
