地铁车辆转向架天线梁模态与疲劳寿命分析

张远维，肖绯雄，杨 强，王腾飞

（西南交通大学牵引动力国家重点实验室，四川成都 610036）

1 引言

地铁列车自动保护系统ATP 天线梁（以下简称“天线梁”）安装在转向架构架上，通过螺栓与构架端部连接在一起，天线梁横梁中部支座用于承载车载信号系统的ATP 天线装置[1]。由于天线梁与构架端部直接相连，安装在构架上的天线梁将不可避免地受到由构架端部传递过来的振动，且由于构架受到轨道不平顺[2]、车轮不圆、车轮缺陷、轮轨冲击等丰富的载荷激励[3]，构架端部传递过来的振动激励与天线梁的固有频率很容易处于同一频带内，这样就会引起天线梁的共振[4]，当天线梁出现强烈振动时，其ATP 系统的功能势必受到影响，导致ATP 天线及信号传输的不稳定，严重威胁到行车安全[5]。

张春玉等[6]依据地铁车辆转向架天线梁实测载荷谱，结合材料的疲劳参数与理论公式对天线梁结构进行随机振动分析与疲劳寿命预测[7]；张春玉等[8]将实测的加速度谱作为仿真的输入条件，结合Dirlik 公式和线性疲劳累积损伤理论，计算得出天线梁的最大损伤位置及其损伤值；蔡川东等[9]根据实测的动应力数据，分析天线梁薄弱处的疲劳寿命，并基于工程应用方案，对天线梁应力集中部位增加加强筋进行结构优化；薛海等[10]基于实测的加速度谱和动应力谱，采用有限元法对天线梁进行随机振动分析，从而确定了天线梁的疲劳薄弱部位；于宏建[11]基于Ansys 的模态分析和谐响应分析，计算出天线梁的工作模态以及在此模态下的响应大小。

为探讨天线梁频繁断裂的原因，本文针对天线梁断裂处和焊缝薄弱处的应力，进行了线路试验、自由和约束模态试验及疲劳寿命分析。

2 天线梁模态分析

2.1 天线梁自由模态分析

模态是结构系统的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型。而自由模态分析是模态分析的一个重要组成部分，它不考虑任何约束的影响，得到的是结构本身的固有特性。通过力锤敲击法测试自由状态下的天线梁模态，并与自由模态有限元计算结果对比，以验证模型的正确性，有限元模型如图1所示，前6 阶模态为天线梁的刚体运动，频率为0，第7 ～13 阶模态对比结果如表1 所示。可以看到，其相对误差较小，证明模型具有较高的准确性。

2.2 天线梁约束模态分析

从理论上来看，自由模态分析不考虑任何约束的影响，能够得出结构的所有振型。但是事实上，实际应用中的结构自由度很多，自由模态得出的频率和振型也有很多，要从诸多结果中获取工程上关心的几个主频是比较困难的。而约束模态由于更多地符合实际边界条件，可以探求在实际运行中约束结构的响应频率是否与外部激励发生共振，从而通过优化结构等方法避开共振频率区域，在工程上有着重要的参考价值。事实上，相比于自由模态，轨道车辆整备状态下，天线梁的边界被约束，其模态振型特性将会发生改变，故计算约束状态下天线梁的模态才能更好地反应出实际运行状况，采用力锤法测试天线梁的约束，其计算结果如表2 所示。

3 动应力分析

了解到天线梁的断裂位置大部分出现在焊缝边缘处，且沿焊缝方向扩展。根据ORE 标准，裂纹朝着垂直于最大主应力的方向扩展，故应变片的贴片方向选择垂直于焊缝，具体测点位置如图2 所示。通过采集到的数据可以发现最大应力幅值出现在天线梁横梁与中间支座焊接处底部的测点T4，在天线梁运动过程中，横梁中部支座受到横向和垂向振动，在弯曲变形和伸缩变形共同作用的情况下，形成了垂直于焊缝的拉压循环。同时，天线梁上其余测点地应力幅值也较大，已经明显超出了正常幅值范围，说明天线梁在运行过程中处于不良受力状态。

本文中的试验工况为镟轮后AW0 工况试验，速度由列车自动驾驶系统（ATO）装置配速，采集到数据，对应力数据进行零漂处理及500 Hz 低通滤波后，最后对应力数据进行频谱分析。图3 为T4 测点在部分区间上的应力速度时域图，图4 为天线梁上部分危险测点的应力频谱图。

图1 ATP 天线梁有限元模型

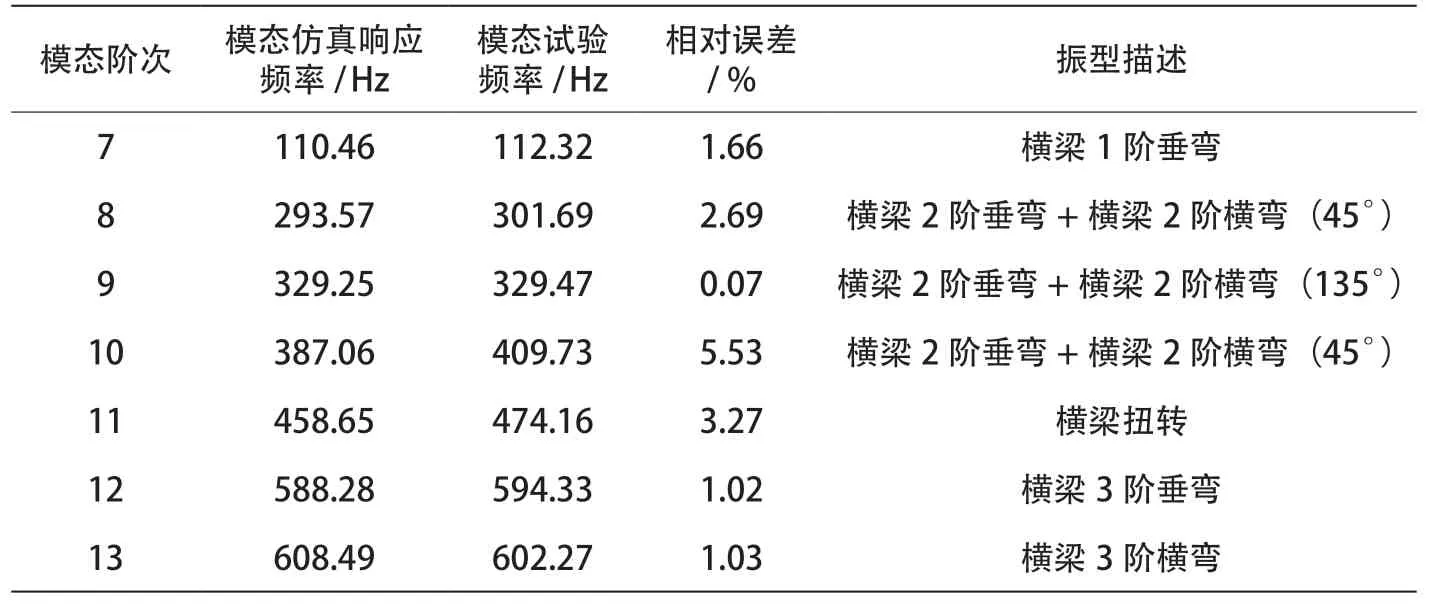
表1 仿真模态与试验模态对比

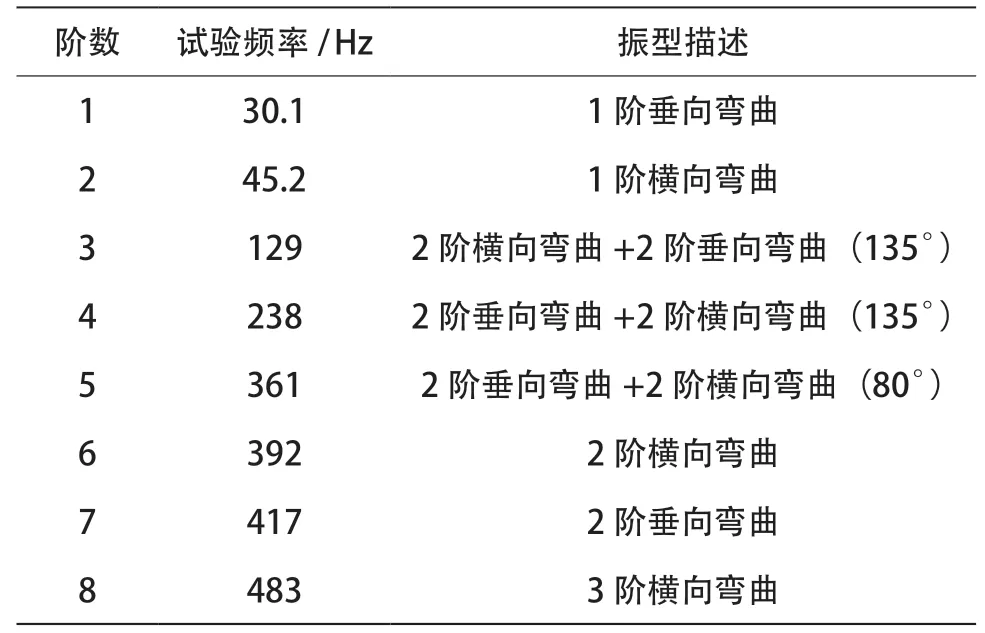
表2 天线梁约束模态

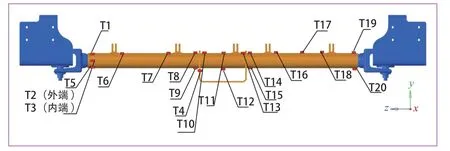
图2 ATP 天线梁测点布置

图3 T4 测点应力、速度时域图

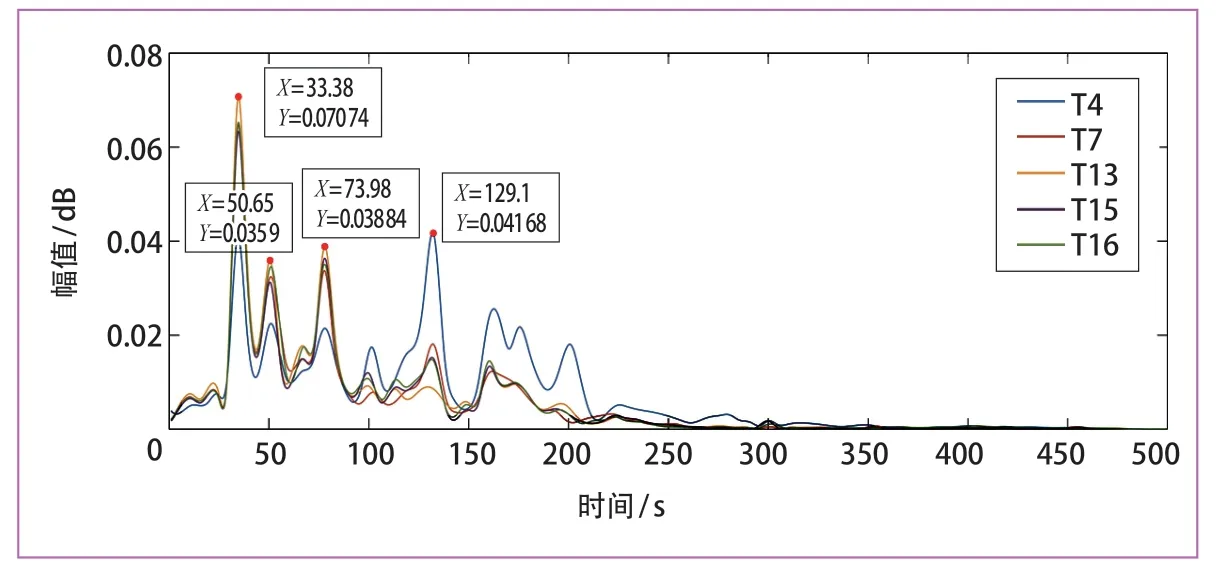
图4 天线梁部分测点应力频谱图

图4 中可以看出，对于不同位置测点的动应力频谱，虽然幅值不尽相同，但其主频成分大致在33 Hz、50 Hz、75 Hz 及129 Hz 左右，其中33 Hz、50 Hz 与129 Hz 左右的应力频谱主频接近于实测的约束状态下天线梁模态的前3 阶频率。由振动理论可知，天线梁很可能存在明显的模态共振，但天线梁的测点动应力频谱中的主频73.98 Hz 并未在实测模态中发现，为找出天线梁的全部主频，避免列车运行时的振动频率与主频在同一频带内，仿真分析了约束状态下构架与装配上的天线梁的模态特性，有限元模型如图5 所示，计算结果如表3 所示。

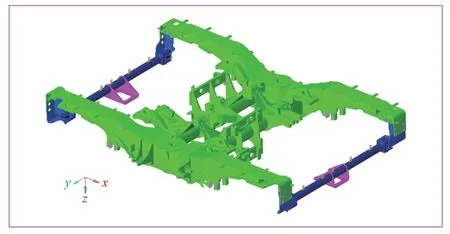
图5 ATP 天线梁与构架有限元模型

从以上仿真出来的模态结果来看，除去构架的模态，天线梁能直接体现出变形的模态频率为：第6 阶35 Hz 左右，第9 阶50 Hz 左右，第11 阶68 Hz 左右，第14 阶133 Hz 左右。但这些模态振型不仅仅是天线梁的单独变形，同时还伴有构架的变形，整体表现为构架与天线梁的耦合振动。对于天线梁测点动应力73.98 Hz 的响应主频，虽未在模态试验中测到，但从仿真计算结果上来看，应该是载荷激励触发了构架的68 Hz 左右的频率，其振型如图6 所示。可以看出，天线梁在这个频率下有明显的1 阶横弯与1 阶垂弯。

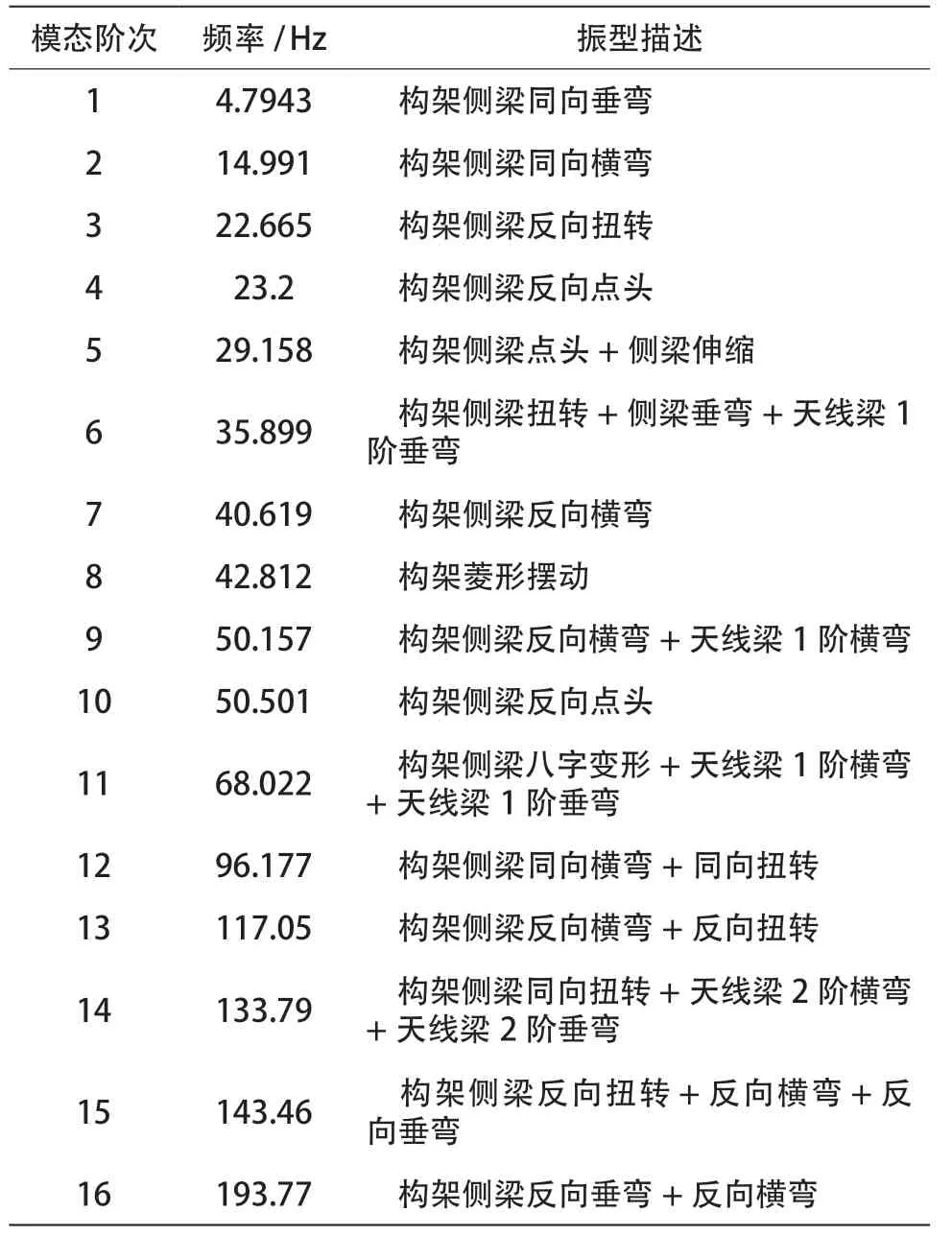
表3 仿真模态与试验模态对比

4 疲劳寿命预测

4.1 测点应力谱

Miner 累积损伤理论表明[12]，应力循环范围及循环次数均对疲劳寿命有较大的影响，为探究应力循环的分布范围以及进行后续测点的等效应力及损伤计算，将采集到的数据经过滤波后进行雨流计数处理[13]，并编制成32 级应力谱。图7 为天线梁上部分动应力测点应力谱，可以看出该测点大部分应力循环范围（σmax- σmin）均处于小范围，但也有应力循环范围较大，已经超过了焊接接头80 MPa 的疲劳极限。

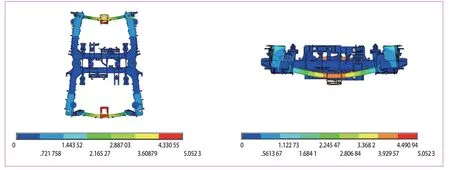
图6 天线梁模态振型图（单位：mm）

4.2 等效应力计算

IIW-1823《焊接接头与部件的疲劳设计标准》[14]表明，在疲劳寿命的评估中，应力谱的应力幅值和应力均值对疲劳寿命均有影响，但是应力幅值对寿命的影响要远远大于应力均值。为直观地反映出测点在整个运营期间的动应力状况以及进行后续测点疲劳寿命的计算，将测点雨流计数后的应力谱外推到整个寿命期间的等效应力Δσe，其具体计算如下：

设实际运行一个试验工况所造成的损伤为D，根据Miner 线性损伤累计法则，有：

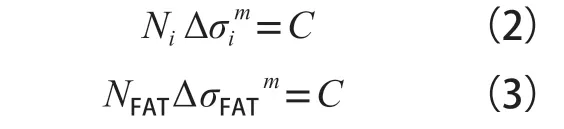
将式（2）与式（3）结合起来，代入式（1）中，可得：

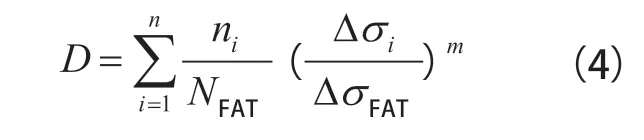
由于等效应力的计算方法本质上是由损伤相等原则推导出来的，将试验工况造成的损伤D 外推到整个寿命区间造成的损伤Dt，有：

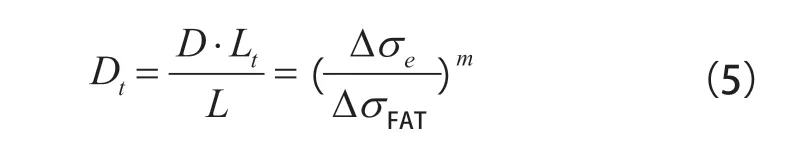
最后得到整个寿命期间的等效应力Δσe：

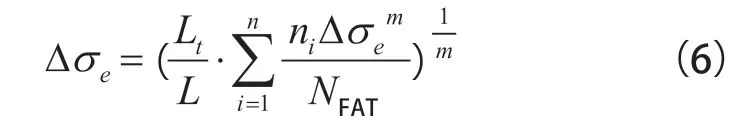
式（1）～式（6）中，n 为应力谱的阶数；ni为第i 阶应力幅在一个工况下的实际循环次数；Ni为第i 阶应力幅在S-N 曲线上所对应的循环次数；Δσi为第i 阶应力幅；Δ σFAT为接头等级所对应焊接接头的疲劳极限；NFAT为在S-N 曲线上疲劳极限所对应的循环次数，取2×106次；Δ σe为等效应力；Ne为等效应力在S-N 曲线上所对应的循环次数；Lt为车辆的安全运营里程数，以整个地铁车辆的设计寿命来要求，取350 万km；L 为列车在一个工况下运行的实际里程数，为66.4 km；m、C 为S-N曲线参数。

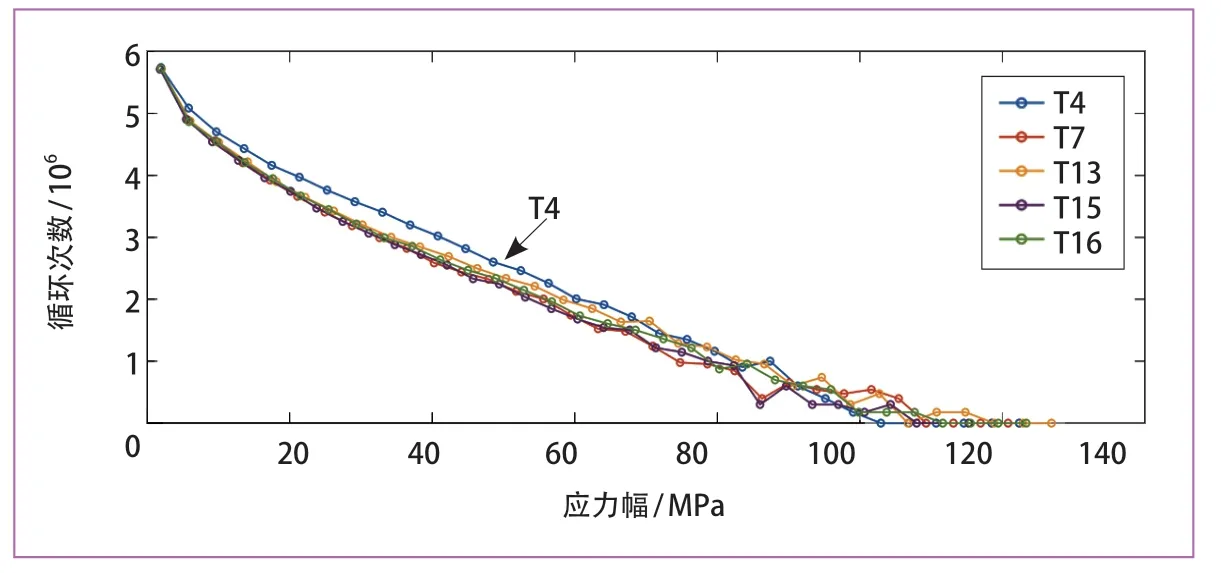
图7 天线梁上测点应力谱

由上述公式可以计算出天线梁上20 个测点的等效应力，如图8 所示。其中，测点T12 和测点T17 属于母材区域，其对应的等效应力为156.4 MPa 和98.85 MPa，按照母材疲劳强度等级（Δ σFAT= 160 MPa）来进行比较，满足疲劳强度要求；然而天线梁上其余18 个测点都属于焊接接头区域，且大部分测点的等效应力已经超出了焊接接头的疲劳强度等级（Δ σFAT= 80 MPa），尤其是T4测点，即天线梁横梁与中间支座焊接处的底部，等效应力已经远远超过焊缝区域的疲劳极限，这说明该测点不仅受天线梁模态振型变形的影响，还受到中间支座安装到天线梁引发的应力集中的影响，故此T4 测点的应力值被大幅度放大。

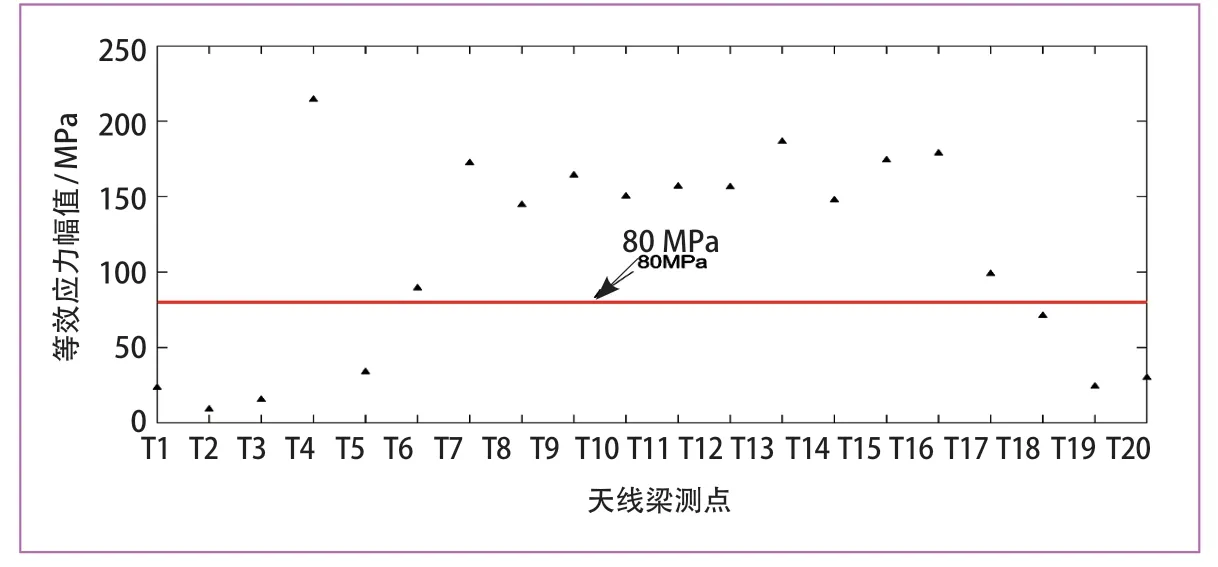
图8 天线梁测点等效应力幅值

4.3 疲劳寿命计算

为计算出天线梁的疲劳寿命，需要先计算试验工况下天线梁的损伤，由于测点分布在天线梁的不同位置上，先要根据IIW-1823《焊接接头与部件的疲劳设计标准》选出每个测点的焊接接头等级，对应不同的S-N曲线，然后根据Miner 损伤累积法则和S-N 曲线进行损伤累积计算，最后线性外推到损伤值达到1 时的运营里程，即天线梁测点疲劳寿命Lt，其具体计算如下：

由式（4）可知，实际运行中试验工况所造成的损伤D 为：

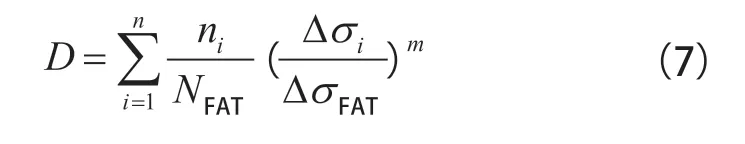
由天线梁测点损伤与测点寿命的线性关系可知：

由式（9）计算出来的部分天线梁测点损伤D 与天线梁寿命Lt如表4 所示。

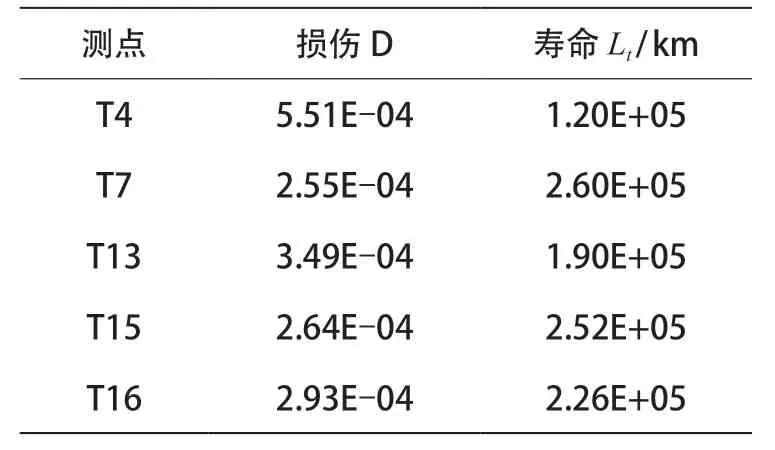
表4 天线梁部分测点损伤值及寿命

5 结论

（1）天线梁的本身模态（33 Hz）及与构架耦合变形模态（75 Hz）均对天线梁的疲劳寿命造成了较大的影响。

（2）由天线梁测点的32 级应力谱可以看出，大部分测点都有超过焊接接头疲劳极限80 MPa 的应力循环次数，这是由于共振效应增大了测点的应力幅值。

（3）T4 测点受到模态振型及应力集中效应的影响，其最大等效应力和最小剩余寿命分别为214.4 MPa 和12 万km，这与设计使用寿命350 万km 相差甚远，可以通过刚度协调原理提高疲劳寿命。