艾拉姆咖分布参数变点的统计推断*
2021-01-22范梓淼田梦琴赫亚伟兰琪暄
范梓淼, 田梦琴, 赫亚伟, 兰琪暄
(新疆农业大学数理学院,830052,新疆维吾尔自治区乌鲁木齐市)
变点问题是统计学中的热门研究方向,在金融、医学、气象学和计算机领域等方面有广泛地应用. 近年来,随着统计分析方法的不断完善,变点问题的发展在理论研究和实际应用上都有了大的飞跃.谭景宝等讨论了Gamma分布的变点问题[1],韩冰凌、孙佳楠对独立泊松与指数序列比较了变点检测方法[2].在方法上,袁芳、韩四儿、谭常春、缪柏其等采用了累积和(CUSUM)方法[3-7],讨论变点的检验与估计问题.
艾拉姆咖分布在研究武器装备维修时间时被提出,目前关于其参数估计取得了一定成果.不同样本下,张月,周菊玲在NA样本下讨论了艾拉姆咖分布参数的经验Bayes检验[8],龙兵在定数双截尾和缺失数据下讨论了参数的估计问题[9,10].潘高田,王保恒,陈春良等讨论了小样本区间估计[11].王敏在复合Linex损失下讨论参数的Bayes估计[12].对于艾拉姆咖分布,易秀龙还讨论了其Pearson-λ2距离及渐近性[13].

1 变点的假设检验

X1,X2,…,Xnτk~F(θ1),Xnτk+1,…,Xn~F(θ2),
其中F(θ)为参数θ的艾拉姆咖分布.
下面考虑如下假设检验问题
H0:θ1=θ2vsH1:θ1≠θ2.
(1)
定义检验统计量为
在显著性水平α下,(1)的拒绝域为
W={(X1,X2,…,Xn):Tk≤A(x,lnn)},


定理1 设X1,X2,…,Xn为来自艾拉姆咖分布的样本,σ2已知,则有
引理1[14]设X1,X2,…,Xn为n个相互独立同分布的随机变量,如果E(Xr)<+∞,r>2,σ2=Var(X)已知,那么存在一列布朗桥过程{W(n)(t),0≤t≤1},n=1,2…,使得当n→∞时,

引理2[14]在引理1的条件下,当n→∞,对0<δ1≤1-δ2<1有
其中{V(t),-∞ 因为 定理1告诉我们,假定选取显著性水平α,通过exp{-2e-x}=1-α,解得 引理3[15]设Y1,Y2,…,Yn为一列鞅差随机变量,假设E(Yi2)=σ2<+∞,i=1,2,…,n.若c1,c2,…,cn为一列非增非负常数,则有 进一步,若令Z1,Z2,…,Zn为随机变量,且对于1≤k≤n,有 E(|Zk|σ(Z1,Z2,…,Zk-1))≥ak|Zk-1|,a.s.; 同时对每一个k有0≤ak≤1.令r≥1,则还有 因为|Tk0|=|Tk0-ETk0+ETk0|≥||Tk0-ETk0|-|ETk0||=|ETk0|-|Tk0-ETk0|, |Tk|=|Tk-ETk+ETk|≤|Tk-ETk|+|ETk|, 所以|Tk|-|Tk0|≤|Tk-ETk|+|Tk0-ETk0|+|ETk|-|ETk0|≤ 另一方面, 所以(ⅰ)当k≤k0时,也就是τ≤τ0,有 (ⅱ)当k>k0时,也就是τ>τ0,有 综上所述,有 而 (2) (3) 再由Burkholder不等式, (4) 其中c1为仅与r有关的常数. 再由Cr不等式, 为验证本文确定的变点位置估计的合理性和有效性,利用R软件进行大量模拟.结果如表1. 表1 变点估计检测结果 表1表明: (1)n越大,估计效果越好,越接近真实值; (2)θ1与θ2相差越大,效果越好; (3)变点真实位置越接近样本中间,估计越准确.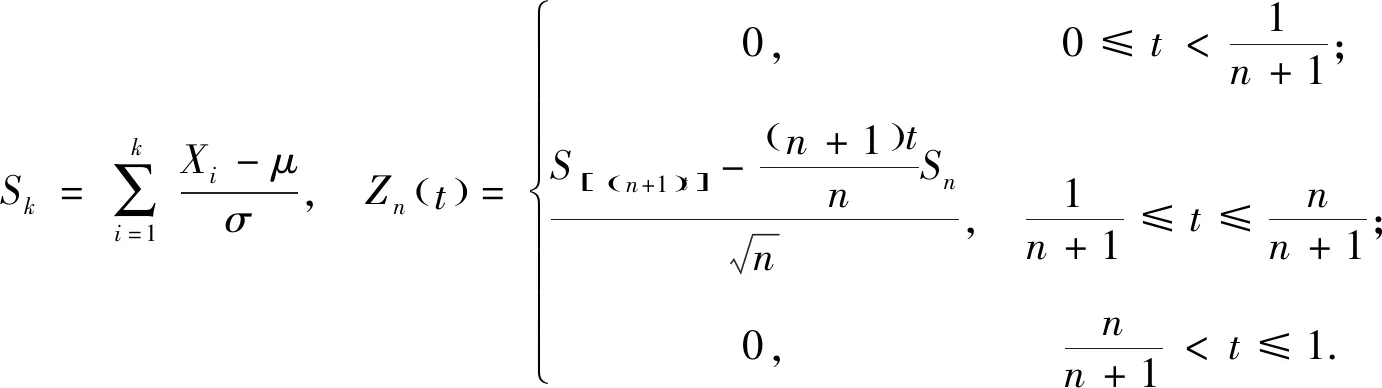


2 变点位置的参数估计

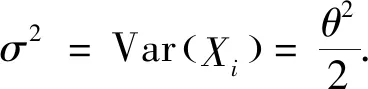













3 数值模拟

