数字化核电厂班组情景意识可靠性评价方法

李鹏程，金 肖，王炎鑫，戴立操，罗筑华

(南华大学 人因研究所，湖南 衡阳 421001)

班组情景意识(TSA)就是两个或两个以上的班组成员在某时刻对当前系统和环境中发生的事件、事件的含义及其未来状态，通过共享各自观点以达到对事物一致的看法和共同理解，在此，TSA被看作是班组成员共同的知识[1-2]。TSA对于高风险系统中的班组任务的成功执行非常重要，像核电厂(NPP)这样复杂工业系统中的系统运行状态监控和异常状态处理，因个人难以完成复杂任务，所以需不同专业知识、技能的人共同来完成[3]。研究表明，像NPP和空中交通管制(ATC)这样的复杂动态系统，其系统安全绩效更多地取决于班组绩效，而不是个人绩效[4]，且班组绩效与TSA呈正相关关系[5-6]。因此，TSA对于NPP的安全至关重要，从而需发展定量方法来对TSA可靠性进行评价以识别班组人因风险，并采取有利措施预防TSA失误的发生。从人因可靠性分析(HRA)的视角来看，TSA可靠性就是在系统运行中的任一阶段，班组在规定的时间和条件下，从环境中收集和处理信息，正确完成对系统状态真实理解的能力。

迄今为止，发展了一些TSA的测量方法来测量TSA的水平[7-8]，但难以识别影响TSA的影响因素及其重要度。尽管一些HRA方法对TSA(相当于诊断)进行了定量可靠性分析，如人的认知可靠性模型(HCR)[9]将班组诊断看作一个整体来进行研究，是一种综合的TSA评价方法，但只考虑有限的3个行为形成因子(PSF)的影响，且3个PSF之间存在相关性。侧重执行型失误(EOC)分析的认知可靠性和失误分析方法(CREAM)[10]通过专家判断确定基本的情景意识(SA)失误概率，通过共同绩效条件(CPC)的评估对基本的人因失误概率(HEP)进行修订，但只考虑了个体的SA，且假设CPC是相互独立的，未考虑PSF的相互影响，如果通过相关性分析来考虑班组的SA可靠性，则会带来诸多的不确定性，使结果产生较大偏差。同样，NUREG-1792[11]和标准化工厂风险分析-人因可靠性分析(SPAR-H)方法[12]也是通过PSF对基本HEP进行修订，存在上述缺陷。

因此，为克服上述缺陷，本文发展一种基于贝叶斯网络(BN)的TSA可靠性评价方法，为提高HRA的质量提供理论支持。

1 TSA因果概念模型

针对NPP数字化主控室运行班组而言，当电厂出现异常情况时，班组需收集和分析信息，识别NPP发生的问题、系统的状态及对所处状态的验证与评估等[13-14]。不同系统的自动化水平(有不同的人机界面特征)、数字化人机界面和数字化规程影响信息的呈现和质量(如信息的醒目性、相关性等)，影响信息的收集和分析，从而会影响TSA[15-17]。当收集到信息之后，班组成员需对信息进行认识、理解和评估，这就需要个体的知识和经验，班组成员的知识和经验水平影响个体的SA水平，从而会影响TSA水平[18-19]。班组知识和经验水平主要受培训水平和班组交流合作水平的影响，以确定班组成员知识的全面性和互补性。由于自动化水平的提高，系统变得更为复杂，任务的高风险后果给个体和班组带来压力，因此，压力会影响TSA等认知行为[20-21]。班组压力主要受任务的复杂性、可用时间及班组知识和经验水平的影响。任务的复杂性决定班组成员需要通过交流与合作来共同完成，交流与合作的充分性影响班组的知识和经验水平，从而影响TSA水平[22-25]。班组为识别系统状态，需收集大量信息，因此信息的显示质量会影响TSA水平，影响信息显示质量的因素主要有数字化规程和人机界面质量[16-17，21]。人因事件分析表明，注意力和态度是影响TSA水平的重要因素[13]，注意力受工作环境的影响(如电话的干扰)，安全态度主要是由电厂的安全文化建设水平决定的。尽管班组情景意识受诸多因素的影响，且相互影响关系非常复杂，但本工作考虑主要的影响因素及其影响关系。此外，研究团队已基于145个人因事件样本数据建立了TSA的因果概念模型(包括班组感知、班组理解和班组评估)[26]，但为了工程应用需对其进行合理简化。因此，通过上述分析并基于专家组讨论(包括模拟机教员2人，具有2～5 a经验的高级操纵员6人，人因专家2人)以修订，最终建立的TSA因果概念模型如图1所示。

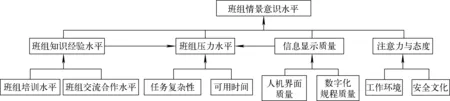
图1 TSA因果概念模型Fig.1 Causal concept model of TSA

2 TSA可靠性定量评价方法

2.1 BN概述

BN是由节点和边组成的有向无环图，可用N=≪V，E>，P>来描述。其中：离散随机变量V={X1，X2，…，Xn}对应的节点表示具有有限状态的变量；有向边E表示节点间的概率因果关系，P为定量部分，是V上的概率分布，对于离散情况，可用条件概率表(CPT)来表示。BN的推理计算是基于父节点所处状态的概率和CPT进行的[27]。

TSA可靠性受诸多PSF的影响，它们之间有相互的影响。图1描述了TSA与各PSF间的因果关系，可用BN理论来进行TSA可靠性的定量评价。其推理算法是基于下列4个方程[28]。

1) 条件独立

(1)

2) 联合概率

P(Y=yj,X=xi)=

P(X=xi)·P(Y=yj|X=xi)

(2)

3) 边缘化定理

P(Y=yj|X=xi)

(3)

4) 贝叶斯定理

P(X=xi|Y=yj)=

(4)

其中：xi为随机变量X处于第i种状态；yj为随机变量Y处于第j种状态。

2.2 先验概率

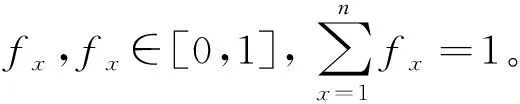
2.3 条件概率

假设父节点X和Y有low、moderate、high 3种状态，子节点Z可能有状态值为low、moderate、high等。通常情况下，父节点状态值与子节点状态值越接近，父节点导致子节点状态的概率越大，如：

P(Z=high|X=high)>

P(Z=moderate|X=high)>

P(Z=low|X=high)

或：

P(Z=low|X=low)>

P(Z=low|X=moderate)>

P(Z=low|X=high)

因此，可建立一种规范化的程序或方法来获取条件概率。

1) 采用层次分析法(AHP)确定PSF的相对重要性

由于不同PSF对TSA可靠性影响的重要程度不同，为确定影响TSA的PSF的相对权重，本文采用AHP对PSF的权重进行辨识。其分析过程主要包括以下步骤[29]：建立层次结构模型；构造成对比较判断矩阵；计算权向量并做一致性检验。

2) 确定考虑权重的父节点状态与子节点状态的距离

由于节点状态之间的距离不同，其概率分布不同，因此采用加权距离绝对值来计算父节点状态与子节点状态之间的距离：

(5)

其中：Dj为父节点状态与子节点处于j状态之间的距离；Dij为第i个父节点的状态与子节点PSF的正考虑的状态之间的距离；n为父节点PSF的个数；j为所考虑的PSF的可能的状态，j=a、b、c，a、b、c分别代表3种不同的状态；wi为第i个父节点的权重。

3) 确定子节点处于不同状态的条件概率分布

针对不同的Dj进行概率分配，采用Roed等[30]建议的概率分布计算公式：

(6)

其中，分子确定子节点PSF处于3个不同状态间的概率分布，分母是用于标准化或归一化的因子，使得3个Pj的和等于1。概率分布情况由定义的分布指数R进行控制，R越大，则子节点PSF处于远离它的父节点状态的某个状态的概率越低。

由式(6)可知，确定PSF的条件概率分布，主要需确定R，在数据缺乏的情况下可通过专家判断来确定。但为减少R的不确定性，基于以前的模拟机实验研究结果[31]，发现同一子节点的父节点PSF之间的相对权重相差比较大的，则R就大，基本相当于他们权重的比值，因此为简化计算，均取同一子节点的父节点PSF之间两者权重较大者之间的比值作为需确定的R，即：

(7)

4) 确定二值变量的条件概率分布

对于像人的可靠性(成功和失败两种状态)这样的二值节点变量，上述计算条件概率的方法不太适用，因此需发展一种新的方法来进行条件概率的识别。为预测操纵员的失误或可靠性概率，需建立函数来表达HEP与PSF之间的关系。

文献[32]构建的人因失误概率f(X)与综合的PSF的影响关系如下：

f(X)=KeλX

(8)

其中：K和λ为两个常量；变量X为所有PSF的综合影响。

依据PSF的相对权重和其状态等级水平来确定PSF的综合影响，进而确定PSF的状态等级水平与HEP的对应关系，确定变量X的方法为：(1) 确定HEP区间，由SPAR-H方法[12]可知，可选择操作失误概率区间为[10-5，1]；(2) 需考虑PSF的权重w和状态等级水平S，以确定他们的综合影响，权重和状态等级水平的取值范围均为[0，1]；(3) 一般而言，当所有PSF的影响处于平均值0.5或所有PSF影响之和等于0.5时，则操纵员的失误概率为名义的失误概率，定义为HEPN，当所有PSF的影响处于0时，则失误概率为1，当所有PSF的影响处于1时，则失误概率为10-5。

因此，所有PSF的影响X可采用以下公式来表示：

(9)

其中：wi为第i个PSF的权重，∑wi=1；xi为第i个PSF的状态等级水平，其取值为区间[0，1]，X的区间为[-1，1]。当xi的取值为0时，X的值为-1，当xi的取值为1时，X的值为1，因此有：

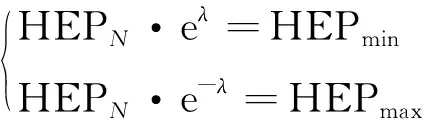
(10)

其中：HEPmin为人因失误的最小值，为10-5；HEPmax为人因失误的最大值，为1。将上述值代入式(9)可得：

(11)

从而可得人因失误概率估计公式为：

HEP=3.16×

(12)

基于式(12)就可确定TSA可靠性或失误的条件概率分布。已知TSA可靠性的因果概念模型及通过构建的评价方法获取的数据，可对TSA可靠性进行定量评价。

3 应用实例分析

选取NPP典型的事故——功率运行期间1台蒸汽发生器中发生1根传热管破裂的事故(SGTR)来进行实例分析，主要任务是隔离破损蒸汽发生器。

3.1 数据获取

1) 根节点的先验概率

由于历史数据和统计数据有限，因此采用专家组对根节点的先验概率分布进行估计。专家组包括2名教员、6名有经验的操纵员和2名人因专家，假定他们的权重一样，经计算得到的综合评估结果列于表1。

表1 影响TSA可靠性的根节点PSF的先验概率Table 1 Prior probability of root node PSF affecting TSA reliability

2) 中间变量的条件概率

(1) 确定PSF之间的相对权重

依据已构建的TSA可靠性因果概念模型，采用AHP对影响TSA可靠性的PSF进行两两比较，得到的相对权重列于表2。

(2) 确定父节点状态与子节点状态的距离

选取PSF“人机界面质量”与“数字化规程质量”影响“信息显示质量”为例进行说明。当父节点“人机界面质量”处于“好(a)”的状态与子节点“信息显示质量”处于“好(a)”状态的距离Daa=0，父节点“数字化规程质量”处于“好(a)”的状态与子节点“信息显示质量”处于“好(a)”状态的距离Daa=0，且其父节点权重分别为wH=0.75、wP=0.25，由式(5)可得其加权距离为Da=0、Db=1、Dc=2。

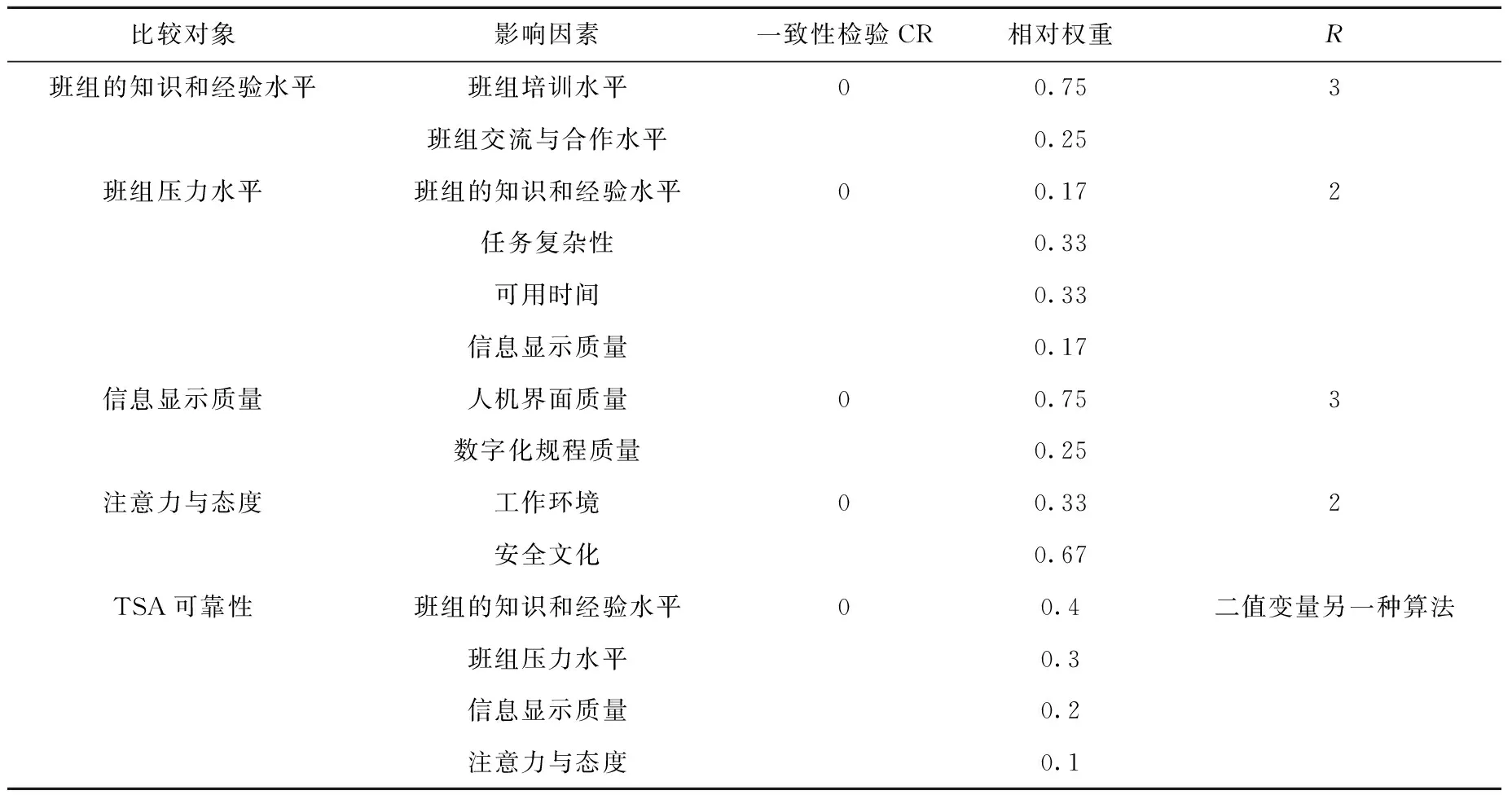
表2 影响TSA的PSF的相对权重及RTable 2 Relative weight and R of PSF affecting TSA

(3) 确定子节点处于不同状态的条件概率分布

首先依据式(7)确定R(表2)，然后计算子节点处于不同状态的条件概率分布，同样以“信息显示质量”为例进行说明。将R=3代入式(6)可得Pa=0.95、Pb=0.047、Pc=0.003，从而可得其条件概率分布分别为0.95、0.047和0.003。同理可得其他条件概率分布。

(4) 确定二值变量的条件概率分布

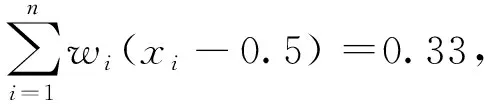
3.2 TSA可靠性定量评价

依据获得的先验概率和条件概率及贝叶斯理论，就可对TSA可靠性进行定量评价。为简化计算，采用匹兹堡大学决策系统实验室开发的可支持贝叶斯推理的软件GeNIe来进行概率推理，主要包括因果推理和诊断推理。

1) 因果推理

因果推理是由原因推知结论，是一种自上而下的推理。在给定原因或证据的条件下，通过贝叶斯推理，求得结果发生的概率。在本例特定情景中，根据与操纵员访谈的情况获得的根节点PSF的状态等级列于表3。然后采用GeNIe软件和已知数据构建TSA可靠性的BN推理模型，得到TSA可靠性为TSAR=0.998，对应的失误概率为TSAE=0.002。

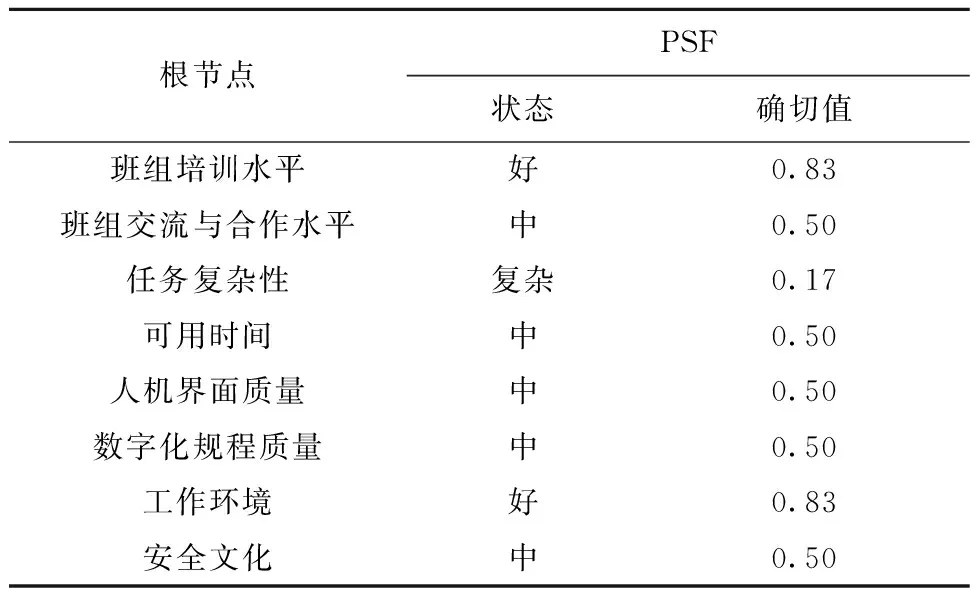
表3 SGTR情境下访谈得到的PSF状态水平Table 3 Level of PSF state obtained from interview in SGTR scenario

2) 诊断推理

诊断推理是由结论推知原因，是一种自下向上的推理过程。当已知结果时，找出产生该结果各种原因的可能性。在本文中假设发生了TSA失误，利用贝叶斯理论公式可计算相应的后验概率，采用GeNIe程序算得的结果如图2所示。将上述后验概率与先验概率(选取最差状态进行对比)进行比较，可得变化的百分比(由后验概率减去先验概率再除以先验概率)，结果列于表4。

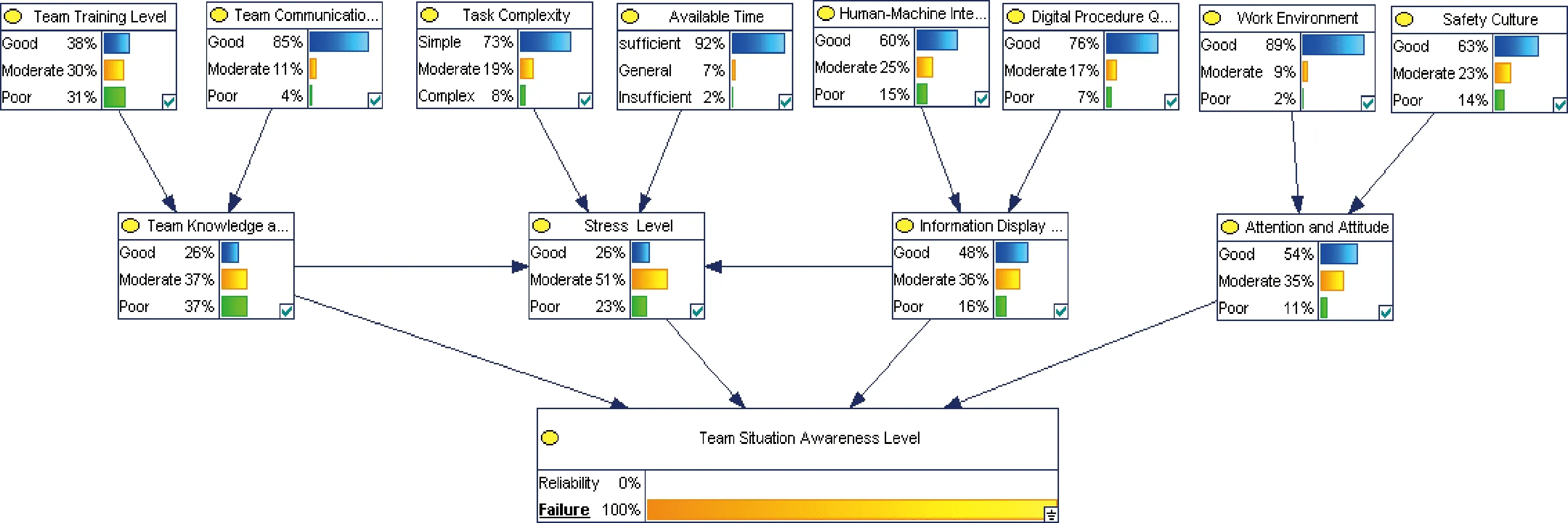
图2 SGTR情景下TSA可靠性分析的BN诊断推理模型Fig.2 Bayesian network diagnostic inference model for TSA reliability analysis in SGTR scenario

表4 根节点变量的先验概率与后验概率的对比Table 4 Comparison of prior probability and posterior probability of root node variable

由表4可知，当发生TSA失误时，班组培训水平差、人机界面质量差、班组交流与合作水平差、可用时间不充分的后验概率与先验概率相比发生了较大变化，分别提高了530%、204%、100%、80%，这表明节点“TSA可靠性”对节点“班组培训水平”、“人机界面质量”、“班组交流与合作水平”、“可用时间”很敏感，这些节点状态的微小波动，可能对班组情景意识失误产生较大影响，成为引发TSA失误的主要原因。

3) 灵敏度分析

为说明本文所构建的TSA可靠性评价模型的有效性和合理性，对其进行简单灵敏度分析，当PSF处于不同状态，获取的TSA可靠性或失误概率不同。当所有PSF状态均取“好”时，失误概率为0.000 147，当所有PSF状态均取“中”时，失误概率为0.004 479，当所有状态均取“差”时，失误概率为0.114 133。因此从整体概率跨度来看，模型构建是合理的。

另外，当其余PSF所有状态均取“好”时，改变班组培训水平的状态，其状态“好”、“中”、“差”分别对应的失误概率为0.000 147、0.000 671、0.002 116。同样，当其余PSF所处状态均取“中”以及“差”时，改变班组培训水平的状态，其状态“好”、“中”、“差”分别对应的失误概率为0.001 537、0.004 479、0.017 278以及0.016 378、0.039 355、0.114 133。

同理可分析其他变量的灵敏度，分析结果示于图3。根据图3可知，其余PSF状态不变，改变某个PSF的状态水平，对应的TSA失误概率不同，说明构建的模型具有较好的灵敏度。

图3 根节点PSF在不同状态下的TSA失误概率Fig.3 TSA error probability of root node PSF in different states

4) 比较验证

为验证本文所构建的TSA可靠性评价方法的有效性，选取2个典型的HRA进行比较分析，分别是CREAM方法[10]和SPAR-H方法[12]。其基本原理为：先确定基本的HEP，然后考虑PSF的影响，再对基本HEP进行修正。CREAM方法采用9个共同绩效条件(CPCs)对基本的HEP进行修订，即组织的充分性(PSF1)、工作条件(PSF2)、人机界面与操作支持的充分性(PSF3)、规程的可用性(PSF4)、需同时考虑的目标数量(PSF5)、可用时间(PSF6)、工作时间段(PSF7)、培训和经验水平(PSF8)、成员之间的合作水平(PSF9)。SPAR-H方法考虑8个PSF的影响，即工作适应性(PSF1)、压力水平(PSF2)、人机界面/工效学(PSF3)、规程质量(PSF4)、任务复杂性(PSF5)、可用时间(PSF6)、工作流程(PSF7)、经验/培训水平(PSF8)。并且不同影响因素分成不同等级，不同等级对应不同的调整值。因此，单个行为的可靠性可用如下公式来计算：

(13)

其中：Pj为第j个行为HEP；BHEPj为第j个行为的基本HEP；PSFk为第k个PSF的调整值，k=1，2，…，m。CREAM方法和SPAR-H方法的分析步聚和数据详见文献[10，12]。由情景环境分析和CREAM方法可知TSA可能的失误模式为“诊断错误”，其对应的基本HEP为2×10-2。由SPAR-H方法可得诊断的基本HEP为1×10-2。具体分析结果列于表5。

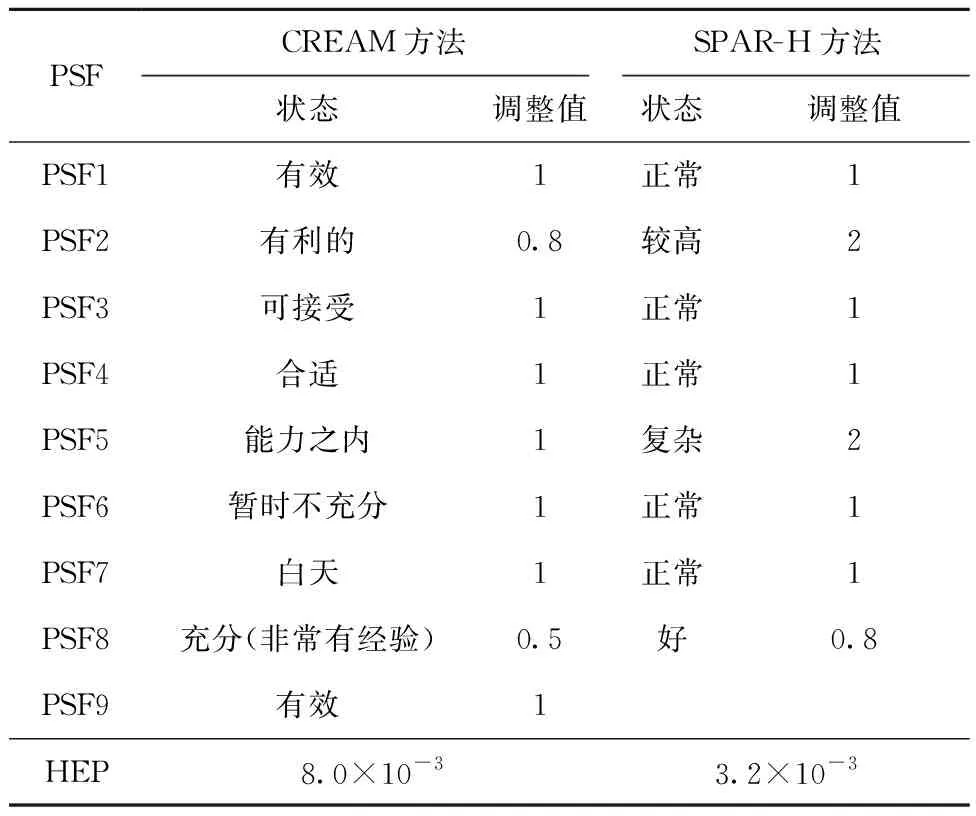
表5 CREAM方法和SPAR-H方法的分析结果Table 5 Analysis result of CREAM method and SPAR-H method

由表5可知，采用CREAM方法识别的HEP为8.0×10-3，采用SPAR-H方法识别的HEP为3.2×10-3。而本文建立的考虑PSF因果关系及权重的可靠性评价方法得到的HEP为2.0×10-3，在同一个数量级，且较CREAM和SPAR-H方法的略低。这说明考虑PSF因果关系及权重的方法用于评估TSA可靠性是有效的。结果产生偏差的原因来源于各方面，如基本HEP、PSF、数据和计算方法的不同。但可以肯定的是，本文建立的方法考虑了PSF之间的相互影响关系与PSF之间的相对权重，从理论分析来看，HEP的计算结果更为准确和合理(但还需进一步实验验证)。另外，本文构建的方法基于BN模型，推理过程具有较强的数理依据，分析过程更具科学性。

4 结论与讨论

TSA对于NPP安全而言特别重要，为识别TSA可靠性水平，克服传统HRA分析方法的不足，本文构建了一种基于BN的TSA可靠性评价方法，得到如下结论。

1) 考虑影响TSA可靠性的PSF相对权重及它们之间的因果关系，克服传统方法在考虑PSF影响时存在双重计算其影响的不足，使方法更加合理，评估结果更符合客观实际。

2) 构建了规范化的中间变量的条件概率计算方法，克服了传统HRA方法基于专家判断带来的不确定性等问题，使获得的概率数据更为合理可靠，提高了数据的质量和分析精度。

3) 案例分析表明，基于BN构建的TSA可靠性评价方法不仅能定量评估特定情景下的人因可靠性(因果推理)，且能识别给定证据情景下(假设发生TSA失误，诊断推理)引发TSA失误的主要贡献因子，为人因失误预防提供理论与实践支持；通过灵敏度分析表明，构建的模型具有较好的灵敏度。同时，经过方法的比较验证，说明该方法有效。

尽管本文方法具有诸多优点，但评估结果的有效性和可靠性还需通过实验来进行验证，发现不足并进行改进，以提升分析的精度，这是未来需进一步研究的工作。同时，TSA可靠性评价过程是一动态过程，因此需进一步收集动态数据和建立动态模型来评估TSA的可靠性，则更符合客观实际。