开口圆柱壳的振动响应分析

张峪维，束永平

(东华大学 机械工程学院， 上海 201620)

板壳式薄壁构件是许多工程结构如压力容器、管道、潜艇船体、飞机的机翼和机身、火箭、导弹以及机器的外壳等最常用的结构元素。壳体的受力主要取决于它的曲率，在保持壳体的厚度和材料不变的条件下改变壳体的曲率，可获得不同的壳体承载能力。因此，曲率、厚度和边界条件等参数是影响甚至决定壳体性能的重要因素。壳体结构的行为特殊性、分析难度以及应用广泛性，引起学者对壳体分析的广泛兴趣。Love[1]通过总结并拓展Rayleigh的工作，构建了Love壳体振动的基本理论。Warburton[2-3]研究了圆柱壳的受迫振动问题，为受径向周期力的壳体求得了强迫振动的模态广义坐标。Leissa等[4]基于Novozhilov理论，讨论了圆柱壳受到正弦波激励的稳态响应问题。但是由于模态耦合的问题，共振响应的峰值和阻尼并不是完全成反比，而是存在微小偏差。Kraus等[5]对均匀薄圆柱壳在谐波径向力作用下的响应进行研究。Liao等[6]得出了圆柱壳对谐波径向力响应的数值结果，预测了圆柱壳在共振时的无限响应。Lu[7]研究了无限长圆柱壳在径向力和黏滞阻尼理论下的响应。

在各种壳体结构中，封闭圆柱薄壳结构被研究得最多。由于圆柱壳的运动方程以及边界条件比梁和薄板复杂得多，因此要得到圆柱壳的解析解是非常困难的，其主要难点在于如何简化和求解这些方程[8]。对于开口圆柱壳的研究主要集中在自由振动(模态和振型)[9]方面，目前文献中尚未见到关于具有阻尼的开口圆柱壳的振动响应分析。

本文利用解析法分析了四边简支开口圆柱壳在简谐激振力作用下的稳态响应，给出壳体在3种不同阻尼下不同位置的径向振幅随激励频率的变化情况。对其与7种开口圆柱壳在前10阶模态频率处的共振响应以及随模态数增加的收敛性进行分析，探究了长径比、厚径比、开口角度对稳态响应的影响。本文提供的开口圆柱壳的振动响应和精度可用于近似求解结构振动响应和精度。

1 开口圆柱壳的计算模型

开口圆柱壳的示意图如图1所示。采用薄壳基本假设[10]：(1)变形前垂直于中面的直线在变形后仍保持直线，并垂直于中面；(2)相对于其他应力分量，沿中面垂直方向的法向应力可忽略不计；(3)忽略壳体的转动惯量；(4)法向挠度沿中面法线上各点是不变的；(5)壳体是等厚度的薄壳，其厚度小于壳体长度和曲率半径的10%。

设壳的厚度为h，中面半径为R，长度为L，开口角度为θ0，在柱坐标系中坐标原点O位于圆柱壳的前端面圆心处，x轴与圆柱壳的轴线重合，z轴沿圆柱壳的径向，切向θ为周向偏转角，u、v和w分别为中面上任意一点P沿轴向、切向和径向的位移。

2 固有频率求解

开口圆柱壳的动力学方程[10]为

(1)

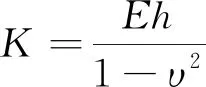
(2)

设四边简支开口圆柱壳的振型解[10]为

(3)

式中：下标m和n表示相应振型沿轴向有m个半波、沿周向有n个半波，对应一组(m,n)有3个频率(i=1, 2, 3)，代表U、V和W彼此的比值不同，但均有m个轴向半波和n个周向半波。3个频率中最低频率对应径向位移较大而轴向位移和周向位移都较小的振动(i=1)，其他两个频率值要比其高一个数量级；中间频率对应轴向位移分量最大而其他两个位移较小的运动(i=2)；最高频率对应周向位移最大而其他位移较小的运动(i=3)。ωimn为固有圆频率[10]。

将此解代入动力学方程得：

(4)

令系数行列式等于零可求解出固有频率系数，再代入式(4)可求得方程组的通解为

C1mn、A2mn、B3mn未知。

3 响应求解

设在壳体中面上一点(ξ,η)处有简谐力作用，其外载荷：qx=0为轴向外载荷，qθ=0为周向外载荷，qz=Poiδ(x-ξ)δ(y-η)ejωt为径向外载荷，其中Poi为径向外载荷幅值。令Poi=1，则式(1)的位移响应解为

(5)

式中：ω为外载荷圆频率；M、N为位移响应叠加量，均为无穷大正整数。

将式(5)代入式(1)，整理得：

(6)

(7)

整理式(7)可得：

(8)

将式(8)两边分别乘以相应阵型(9)，并对开口圆柱壳的中面进行面积分，整理得式(10)。

(9)

(10)

求解方程组(10)即可得出响应值系数Aimn、Bimn和Cimn。

4 计算实例与分析

7种开口圆柱壳的材料参数均为E=2.1×1011Pa，泊松比υ=0.3，密度ρ=7 850 kg/m2；复阻尼系数γ分别取0.01、 0.05和0.20。开口圆柱壳的材料参数与尺寸参数如表1所示，其中，L/R为长径比，h/R为厚径比，θ为开口角度。

表1 开口圆柱壳的材料参数与尺寸参数

由于m、n为偶数时其对共振响应的贡献很小，因此本文在算例中仅取对共振响应贡献较大的前10个模态进行计算对比。表1中壳体Ⅰ在点(L/2,θ/2)处激励频率分别等于前10阶模态频率时，简谐激励在点(L/2,θ/2)处复阻尼系数分别为0.01、 0.05和0.20情况下的共振响应数据，以及级数解中包含不同模态阶数的结果与外载荷激励频率等于零时(静态)的结果如表2所示。其中：A表示只考虑激励频率等于当前m/n计算得到的固有频率的响应；B表示N=5、M=15时的响应级数解，N、M均为位移响应收敛解叠加的项数；C表示N=19、M=25时的响应级数解，此时级数解已收敛，对比计算可知其相对误差小于0.1%；D表示N=30、M=30时的响应级数解。静态响应与复阻尼系数之间的关系很小，因此，非静态共振响应的峰值随着复阻尼系数增加而减小。

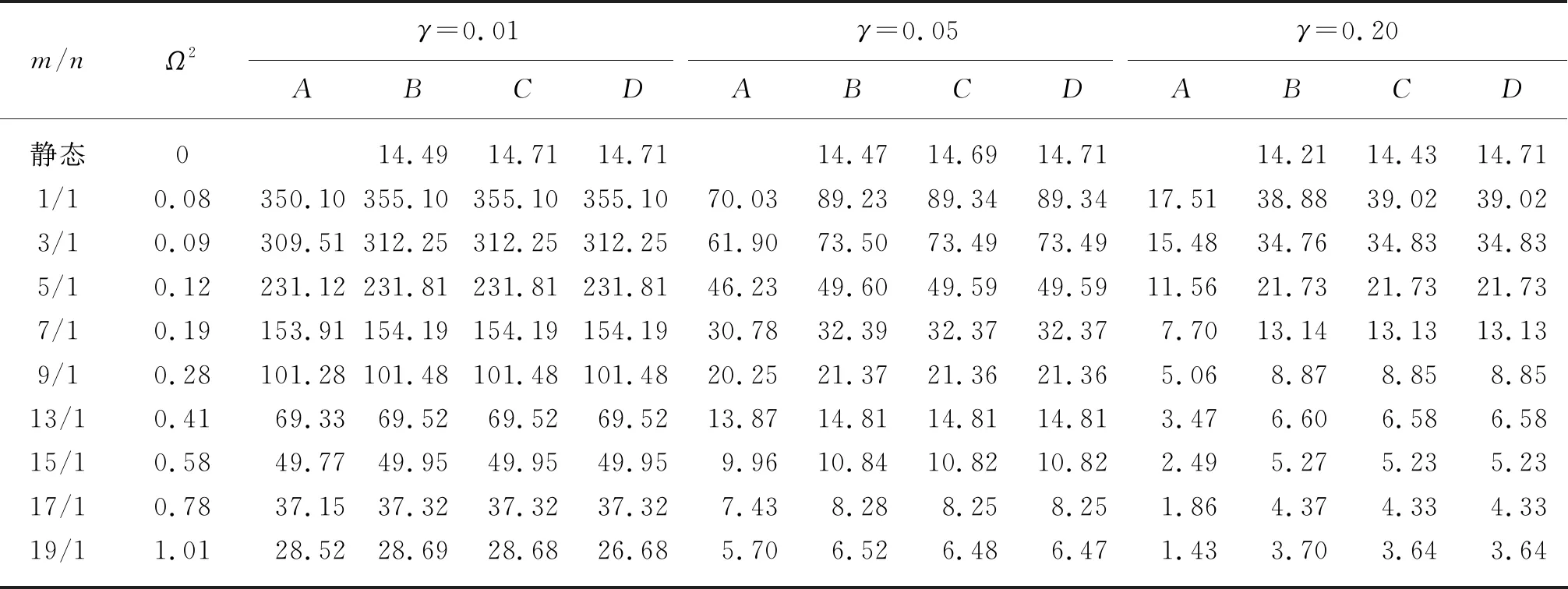
表2 开口圆柱壳Ⅰ在点(L/2, θ/2)处的响应

开口圆柱壳Ⅰ在点(L/2,θ/2)处外激励频率与m=19、n=1固有频率相等时的振动响应级数解与M、N之间的关系如图2所示，其中，纵轴标题|w(L/2,θ/2)ER/P|×10-3表示无量纲位移响应幅值。

由图2可知，随着M、N的增加，响应级数解值逐渐趋于平稳收敛，并且M值对响应级数解的影响较大，而N对响应级数解的影响较小。通过计算可知，当N=19、M=25时响应级数解收敛。

开口圆柱壳Ⅰ、Ⅱ、Ⅲ响应值的变化特性与长径比之间的关系如图3所示。由图3可知：响应值随外载荷频率的增加而减小；随长径比的增加，共振点的峰值减小，相邻固有频率之间的间距减小，共振峰间距减小，而远离共振峰的响应基本未发生变化，即长径比的大小对远离共振峰的响应影响较小。

开口圆柱壳Ⅲ、Ⅳ、Ⅴ响应值的变化特性与厚径比之间的关系如图4所示。由图4可知：随着厚径比的增大，远离共振点和共振点附近响应值明显减小；随着厚径比的变化，共振点的位置发生大幅度偏移，并且相邻共振峰之间的间距随着厚径比的增大而增大。

开口圆柱壳Ⅴ、Ⅵ、Ⅶ响应值的变化特性与开口角度之间的关系如图5所示。由图5可知：随着开口角度的增大，一阶固有频率减小，共振峰的峰值增大，相邻共振峰之间的距离增加；开口角度对远离共振峰的响应值也有一定的影响，但随着开口角度的增大，其影响程度逐渐降低。

开口圆柱壳Ⅰ在3种不同复阻尼系数下，在点(L/8,θ/2)、(L/4,θ/2)和(L/2,θ/2)处施加集中简谐力的无量纲响应与外载荷频率系数的变化关系如图6所示，其中，每幅图的上横轴标记了对应的固有频率阶数(m/n)的位置。

由图6(a)可知：当γ=0.01时，m/n=1/1的峰值小于3/1时的峰值；随外激励频率的增加，响应峰值出现波动。这是由开口圆柱壳振动过程中轴向不同位置的响应变化规律不同所引起的。随阻尼系数γ的增大，间距较小的两个峰值间出现共振峰合并现象。当γ=0.05时，m/n=1/1的共振峰被吸收，无明显的峰值；γ=0.20时，除第1个共振峰被清晰地显示出来外，其他的共振峰均明显受到了抑制，并随固有频率的增大逐渐趋于平稳。

由图6(b)可知：当γ=0.01和0.05时，随外激励频率的增加，响应峰值逐渐减小；随着阻尼的增大，间距较小的两个峰值间也出现了共振峰合并现象。当γ=0.20时，所有共振峰均无明显的峰值，且响应随着固有频率的增大逐渐趋于平稳。

由图6(c)可知：当γ=0.01和0.05时，随外激励频率的增加，响应峰值逐渐减小；随阻尼的增大，未出现共振峰合并现象。当γ=0.20时，除m/n=1/1时共振峰明显的峰值未被抑制外，其余均被抑制，且响应随固有频率的增大逐渐趋于平稳。

图6表明，共振峰不仅与固有频率有关，还与阻尼大小有关，且随阻尼的增大，共振峰的峰值逐渐减小。当距共振峰较远时，复阻尼系数γ=0.01和0.05的响应曲线在非共振位置是无法区分开的，在这种情况下一般默认选用γ=0.05对应的响应曲线。

5 结 语

本文从圆柱壳的动力学方程出发，考虑复阻尼的影响，确定了在径向简谐激励作用下，四边简支开口圆柱壳在7种不同结构参数和3种复阻尼系数的响应，讨论结构参数、材料参数、激振点与位移响应的关系。主要结论总结如下：

(1) 开口圆柱壳的厚径比、长径比和开口角度对振动响应的影响较大，选择合适的结构参数对于解决不同工程中的振动问题而言是非常重要的；

(2) 开口圆柱壳的长径比、厚径比、开口角度不仅对振动响应幅值有影响，也对振动固有频率有很大影响，因此在设计时应根据工况中载荷频率的范围来确定开口圆柱壳的结构参数；

(3) 于同一位置施加载荷的不同则位置的振动响应有所不同，在考虑去除最大共振对于开口圆柱壳的影响时，应考虑壳体不同点的振动响应；

(4) 随复阻尼系数的增大，开口圆柱壳的振动响应幅值逐渐减小。