随机时滞微分方程的截断Caratheodory数值解的收敛性
2021-01-21蔡雨欣王子丰尤苏蓉
蔡雨欣, 王子丰, 尤苏蓉
(东华大学 理学院,上海 201620)
在随机时滞微分方程(stochastic delay differential equations, SDDEs)的研究中,当系数满足局部Lipschitz条件和线性增长条件时,方程的解存在且唯一。但很多的SDDEs并不满足线性增长条件,针对这类方程,文献[1]指出系数满足Khasminskii型条件时,方程的解存在且唯一。
随机微分方程(stochastic differential equations, SDEs)的精确解通常很难求出,构造方程的数值解并分析数值解的相关性质是SDEs的热门研究课题,常用的数值方法有Euler-Maruyama法、倒向Euler-Maruyama法、驯化Euler-Maruyama法、Milstein法以及Caratheodory法。目前,系数满足局部Lipschitz条件和线性增长条件的SDEs方程的数值解已得到广泛研究[2-6]。
对于非线性增长条件下SDEs的数值解问题,也有相关研究报道。如Hutzenthaler等[7]在高度非线性增长条件和单边Lipschitz条件下研究了这类方程的数值解。文献[8-9]提出的截断Euler-Maruyama法,可以用于求解系数满足局部Lipschitz条件和Khasminskii型增长条件的方程的数值解。此后,截断Euler-Maruyama法被应用于SDDEs的数值解分析中,得到了具有强收敛性和收敛速率的数值解[10]。文献[11]利用截断Caratheodory数值算法探讨了SDEs数值解的收敛性。截断算法在SDDEs的应用主要是截断Euler-Maruyama法与局部截断Euler-Maruyama法,目前还没有将截断思想应用于SDDEs的Caratheodory数值解的相关文献报道。本文将这种数值算法应用于SDDEs中,进而证明数值解的强收敛性。
1 问题背景及截断Caratheodory数值算法构造
若x∈n,用|x|表示其欧几里得范数。若A是一个向量或是矩阵,使用AT表示其转置,用表示它的迹范数。给定τ>0,用表示定义在[-τ, 0]上,取值于n的连续函数族。对于设(Ω,F, {Ft}t≥0,P)是一个完备概率空间,{Ft}t≥0是其上的一个σ域流,满足通常条件[10](单调递增且右连续,F0包含的所有P为零测集)。B(t)=(B1(t),B2(t), …,Bm(t))T是定义在该概率空间上的m维布朗运动。对于两个实数a和b,记a∨b=max(a,b),a∧b=min(a,b)。对于给定实数a,用[a]表示小于等于a的最大整数。
考虑如式(1)所示的随机时滞微分方程。
dx(t)=f(x(t),x(t-τ))dt+
g(x(t),x(t-τ))dB(t),t≥0
(1)
式中:f(x,y):n×n→n,g(x,y):n×n→m×n分别为方程的漂移系数和扩散系数;τ>0为时滞量。
初值条件为
{x(θ): -τ≤θ≤0}=ξ∈C([-τ, 0];n)
(2)
假设式(1)的系数满足以下局部Lipschitz条件和Khasminskii条件。
假设1对任意的h>0,存在Kh>0使得

假设2存在一组常数p>2和K>0,使得对任意的x,y∈n有

传统解的存在唯一性定理要求方程的系数满足局部Lipschitz条件和线性增长条件。在局部Lipschitz条件和Khasminskii条件下,方程具有非线性特征,引理1给出了这类方程的解的存在唯一性。

为定义截断Caratheodory数值格式,首先选定一个严格单调递增的连续函数μ:+→+使得当r→+∞时,得μ(r)→+∞,且对任意的r≥1有
(3)
记μ-1为函数μ的反函数,则μ-1:[μ(0), +∞)→[0, +∞)是严格单调递增的连续函数。取定一个常数Δ*∈(0, 1]和一个严格单调递减的函数h:(0,Δ*]→(0, +∞)使得对任意的Δ∈(0,Δ*]都有
(4)
对于给定的步长Δ∈(0,Δ*],定义映射πΔ:n→{x∈n: |x|≤μ-1(h(Δ))}如下:
当x=0时,定义πΔ(0)=0。因此,πΔ(x)将任意一个向量x映射到一个半径为μ-1(h(Δ))的球的内部。对任意的x,y∈n,定义如下截断函数
fΔ(x,y)=f(πΔ(x),πΔ(y))
gΔ(x,y)=g(πΔ(x),πΔ(y))
由式(3)得
|fΔ(x,y)|∨|gΔ(x,y)|≤
μ(μ-1(h(Δ)))=h(Δ)
(5)
这表明,无论f和g是否有界,其截断函数fΔ和gΔ都是有界的。引理2说明截断函数fΔ和gΔ仍然满足Khasminskii条件。
引理2[13]令假设2成立,那么对于Δ∈(0,Δ*],对任意的x,y∈n有

当-τ-Δ≤t≤-τ时,定义xΔ(t)=x(-τ);
当k=-M,-M+1,…,0时,定义xΔ(tk)=ξ(tk);
当k>0,tk (6) 显然, (7) dxΔ(t)=fΔ(xΔ(t-Δ),xΔ(t-τ-Δ))dt+ 本文主要研究常时滞方程的数值解设计,对于变时滞方程情形,需要对上述数值解格式进行适当的调整,变时滞方程如下: dx(t)=f(x(t),x(t-δ(t)))dt+ 为证明数值解的收敛性,首先给出式(1)的精确解和数值解所具有的一些基本性质及引理。 定理1对于任意的Δ∈(0,Δ*],t≥0有 (8) 其中Cp是仅与p有关的正常数,进而有 (9) 证明:由式(7)可得 从而有 由基本不等式|a+b|p≤2p-1|a|p+2p-1·|b|p,Hölder不等式以及矩不等式,上式可变形为 再由式(5)得 显然有式(9)成立。 引理3若假设1和假设2成立,则 (10) 其中C是与Δ无关的正实数。 证明:对|xΔ(t)|p使用It公式可得 利用引理2以及Young不等式可得 (11) 再利用定理1以及式(4)和(5)可得 (12) 将式(12)代入式(11)得 (13) 其中C3=C1+CpT,C4=3C2,且Ci(i=1,2,3,4)是与Δ无关的正实数。 由于式(13)对任何的t∈[0,T]都成立,其不等号右边是关于t非降的,因此 进而利用Gronwall不等式可推出 (14) 其中C=C3eC4T,且不依赖于Δ,从而式(10)成立。 下文引理4和5说明了式(1)的精确解和数值解所定义的两个停时的性质,这两个引理将在定理2证明数值解的收敛性时有用,其中引理4关于精确解的性质在文献[8]中已有证明,这里仅引用其结论。 引理4[8]令假设1和假设2成立,则对任意实数R>‖ξ‖,定义停时 τR=inf{t≥0:|x(t)|≥R} (15) 引理5令假设1和假设2成立,对任意实数R>‖ξ‖,Δ∈(0,Δ*],定义停时 ρΔ,R=inf{t≥0:|xΔ(t)|≥R} (16) 则 (17) 其中C9是与Δ,R无关的正实数。 证明:将ρΔ, R简记为ρ,对任意0≤t≤T,应用It公式可得 根据引理2,上述不等式可以变形为 (18) 分析式(18)不等号右边的第一个积分 (19) 式中,C6=4K1T(1+E‖ξ‖2)。 基于引理1以及式(4)和(5),式(18)不等号右边的第二个积分可以放缩为 (20) 将式(19)和(20)代入式(18)可得 (21) 由于式(21)不等号右边关于t是非降的,因此 (22) 由定理2证明截断Caratheodory数值解的收敛性,为此需要对初值函数添加一定的条件,该条件在其他数值解的收敛性分析中也有使用[8-9]。 假设3存在一组常数K2>0,γ∈(0, 1],使得初值ξ满足 |ξ(u)-ξ(v)|≤K2|u-v|γ,-τ≤v≤u≤0。 定理2若假设1~3都成立,则对任意的q∈[2,p),有 (23) 证明:令τR,ρΔ, R与式(15)、式(16)定义相同,并记θΔ,R=τR∧ρΔ, R及eΔ(T)=xΔ(T)-x(T)。利用Young不等式,对于任意δ>0,有 E|eΔ(T)|q=E(|eΔ(T)|qI{θΔ, R>T})+ E(|eΔ(T)|qI{θΔ, R≤T})≤ (24) 由引理1和引理3可知 E|eΔ(T)|p≤C (25) 又由引理4和引理5得到 (26) 其中C10=C5+C9。将式(25)和(26)代入式(24)可以推出 (27) 为此定义两个截断函数 令Δ*足够小,且满足μ-1(h(Δ*))≥R,因此对Δ∈(0,Δ*),有 fΔ(x,y)=FR(x,y),gΔ(x,y)=GR(x,y),其中x,y∈,|x|∨|y|≤R。 考虑式(28)所示的随机时滞微分方程。 dz(t)=FR(z(t),z(t-τ))dt+GR(z(t),z(t-τ))dB(t) (28) 初值为z(u)=ξ(u),u∈[-τ, 0],其中FR(x,y)和GR(x,y)满足全局Lipschitz条件。因此,式(28)在t≥-τ上有唯一的全局解z(t),且 x(t∧τR)=z(t∧τR) , 0≤t≤T (29) 设zΔ(t)为式(28)的Caratheodory数值解,则同样可得 x(t∧ρΔ,R)=z(t∧ρΔ, R) , 0≤t≤T (30) 关于式(28)的Caratherodory数值解zΔ(t)与全局解z(t)两者的关系,由文献[5,14]的结论可得 其中H为依赖于KR,T,ξ,q,且与Δ无关的正常数。因此 再结合式(29)和(30),上式即为 因此, 从而只要Δ足够小,式(27)成立,即可证明式(23)成立,即数值解强收敛于精确解。 考虑下面的非线性一维随机时滞微分方程。 dx(t)=(-2x3+2x(t-τ))dt+(|x(t)|3/2+ 其初值为 xt0=ξ={cosθ:-1≤θ≤0}。 显然,此方程满足假设1,同时 满足假设2。 利用Matlab软件进行数值模拟,得到如图1所示的截断Caratheodory数值解。 相比文献[11]所讨论的不带时滞项的随机微分方程数值格式,本文所得到的结论是对[11]关于数值格式稳定性结论的推广和补充。如果将算例中的时滞项舍去,那么该算例能够满足文献[11]进行相关分析所需的条件,因此数值解也将有相应的收敛结论。 本文使用截断Caratheodory法研究了非线性随机时滞微分方程的数值解的强收敛性。对于给定的步长Δ,定义了离散时间下的截断Caratheodory数值解,随后构造了连续时间的截断Caratheodory数值解 xΔ(t),在局部Lipschitz条件和Khasminskii型条件下,证明了连续时间的截断Caratheodory数值解强收敛于其精确解。
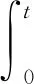
gΔ(xΔ(t-Δ),xΔ(t-τ-Δ))dB(t)
g(x(t),x(t-δ(t)))dB(t),t≥0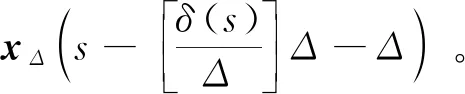
2 截断Caratheodory数值解的收敛性



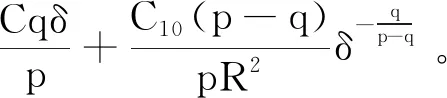

3 算 例
sinx(t-τ))dB(t),t≥0
4 结 语
