基于障碍物运动预测的移动机器人路径规划

杨奇峰，曲道奎，徐 方

(1.中国科学院沈阳自动化研究所机器人学国家重点实验室，辽宁 沈阳 110016；2.中国科学院机器人与智能制造创新研究院，辽宁 沈阳 110169；3.中国科学院大学，北京 100049；4.沈阳新松机器人自动化股份有限公司，辽宁 沈阳 110168)

0 引 言

移动机器人路径规划技术是其研究的关键技术问题之一，移动机器人局部路径规划方法可以归类为3类方法，基于图搜索的路径规划技术[1-3]，构建人工势场进行路径规划的技术[4]，基于各类人工智能算法的路径规划技术[5-8]，各种算法各有优缺点[9]。

刘军等提出有向D*算法。该算法考虑目标点与障碍物信息，引入关键节点概念，较传统算法能更好地兼顾局部搜索与全局最优性[10]；Le AT等基于D*lite在复杂环境中的效率问题，提出了一种新的算法D*LR(D*lite with reset)，在复杂环境下，D*LR的性能比D*lite有明显的提高并在ROS上进行了验证[11]；黄鲁等引入懒惰视线算法，结合距离变换对D*lite算法进行改进。使得重规划得到的路径远离突现的障碍物[12]。杨俊驹通过改进传统人工势场法作为机器人局部路径规划算法，使机器人能迅速避开动态障碍物[13]。吴运雄等提出基于深度强化学习的动态避障算法，较好地解决了传统算法存在的容易陷入局部最优的问题[14]。这些算法在进行动态路径规划时，在每一个更新的时刻，机器人都是根据障碍物的当前位置进行后续路径规划，并依次更新迭代，在机器人动态的更新路径时，并不考虑动态障碍物的运动趋势，因此我们希望在移动机器人动态路径规划时，引入动态障碍物的运动预测机制，优化动态避障路径规划策略。在移动机器人的动态避障路径规划过程中，评估障碍物的移动轨迹，提出改进的D*lite路径规划算法，使机器人的动态避障算法更接近于人的避障策略，提高机器人动态避障路径规划的效率和安全性。

1 基于D*lite的路径规划

D*lite是一种基于栅格模型适应动态环境的路径规划算法。D*lite算法由D*算法改进而来，运用LPA*算法的思想，使得移动机器人在未知动态环境下可以快速重规划。

D*lite算法与D*算法一样，搜索方式采用从目标节点到起始节点，以适应起始点改变的情况，D*lite算法维护每一个节点的g(s)， 并且引入了LPA*算法中rhs(s) 的定义

(1)

式(1)中用Succ(s) 表示所有节点s的后继节点，用g(s′) 表示节点s′到目标节点的距离代价。 D*lite维护每个栅格的g(s) 与rhs(s)， 当两个变量相等时，定义该节点为一致状态，否则为不一致态。只有处于一致状态下的节点是已经扩展完毕、可以通行的，不一致状态表示该节点的路径信息是不准确的。 D*lite算法如图1所示。

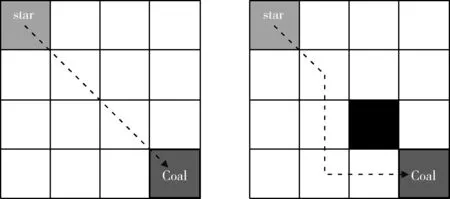
图1 D*lite算法

D*lite算法引入k(s) 来进行各栅格节点的距离代价的评估，k(s) 包含两个值[k1(s);k2(s)]， 这里的k1(s)，k2(s) 由如式(2)、式(3)计算

k1(s)=min(g(s),rhs(s))+h(s,sgoal)

(2)

k2(s)=min(g(s),rhs(s))

(3)

当环境中出现新的障碍物时，D*lite算法可以快速更新该障碍物周边节点的信息，并对由此而导致不连续的节点进行快速重规划。但是每次机器人遇到新的障碍物进行避障时，机器人总是只考虑障碍物当前的位置，并不考虑障碍物的动态性，因此对于动态障碍物的避障，所规划出的路径并不是最优的。另一方面很有可能机器人选择的避障路径与障碍物的运动方向一致，增加了机器人与障碍物碰撞的风险，本文提出基于障碍物运动趋势的改进D*lite算法，极大提高了局部动态障碍物避障路径规划的规划效率及安全性。

2 基于动态障碍物运动趋势的避障路径规划

2.1 基本原理

人在行走过程中，如果在自己的行走路线上出现诸如行人、汽车等运动障碍物，会首先基于运动障碍物的历史移动轨迹及当前状态分析其运动意图，之后根据运动障碍物的运动意图合理规划下一步路线。本文提出了基于运动障碍物运动意图的动态障碍物路径规划方法，如图2所示，模仿人遇到动态障碍物的避障策略。在进行运动障碍物避障时，首先分析运动障碍物的意图，以提高避障的效率和安全性。

图2 动态避障路径规划

机器人通过对运动障碍物历史状态的分析，估计运动障碍物速度及在避障过程中运动方向和运动距离，将运动障碍物的可能行走轨迹作为待避障区域的一部分进行整体规划。在所有可行的轨迹中，采用时间维度上路径最优的策略确定优先级最高的路径，机器人运行过程中实时判断运动障碍物的状态，并不断调整运行轨迹。局部动态避障算法步骤如下：

(1)机器人实时采集环境中障碍物的信息，并计算障碍物在环境坐标系下的历史位置；

(2)对障碍物进行合理的膨胀，提高机器人避障路径规划的安全性；

(3)根据障碍物的历史位置，基于障碍物运动预测模型预测机器人运行过程中障碍物的行进路径；

(4)采用改进D*lite算法实时规划机器人行进的路径，控制机器人按照规划路径运行；

(5)机器人运行过程中根据障碍物状态(历史轨迹)的变化，实时调整机器人的运行轨迹。

2.2 动态障碍物的探测与运动趋势预测

机器人可以通过自身搭载的摄像头、机载雷达等传感器实时获取环境中的点云信息，采用聚类的方法对环境中的物体点云进行归类，并实时对环境中的障碍物进行匹配分析，不同帧数据中障碍物的位置变化表征了动态障碍物的历史移动轨迹。

如图3所示， R为移动器人， O为机器人探测到的前方障碍物。在机器人R运行过程中，障碍物O同时也在运动，机器人当前的位置为Pr， 速度为Vr， 动态障碍物当前的位置为Po， 速度为VO， 下一时刻动态障碍物运行的可能位置为P′o， 对运动障碍物进行运行轨迹预测可以提高机器人的路径规划效率。

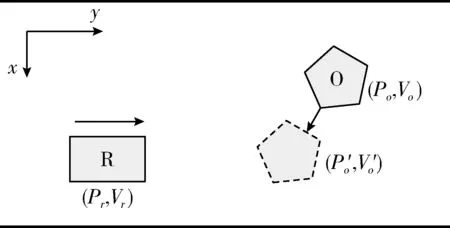
图3 动态障碍物运行趋势

设运动障碍物任意时刻的位置为Pi=(xi,yi)， 运用拉格朗日插值法建立移动目标的运动轨迹模型。

采用拉格朗日插值法可以构建一个多项式，该多项式在各个观测点通过观测到的值，对于任意K+1个点A0(x0,y0),A1(x1,y1),…,Ak+1(xk+1,yk+1), 存在多项式(4)

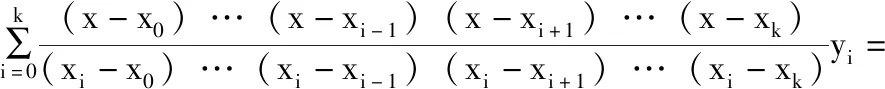
(4)

其中，li(x) 为拉格朗日基本多项式，也称为插值基函数，其表达式为(5)

(5)

拉格朗日插值多项式fk(x) 的截断误差为公式

(6)

其中，cn+1(x)=(x-x0)(x-x1)…(x-xn)， 因此，三点外插公式为式(7)和式(8)

(7)

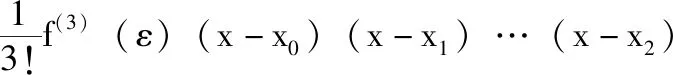
(8)

设机器人在运行过程中，通过扫描匹配获得动态障碍物的先后3个位置为(ti,xi,yi)，(ti+1,xi+1,yi+1),(ti+2,xi+2,yi+2)， 由上式可以得出动态障碍物tn时刻x方向和y方向的运动预测计算公式，分别为式(9)、式(10)

(9)

(10)

模型建立后，即可计算出此后任意时刻tn运动目标的位置 (tn,xn,yn), 当机器人运行过程中获得新的动态障碍物位置，设为 (ti+3,xi+3,yi+3)， 这时令

ti=ti+1,xi=xi+1,yi=yi+1

(11)

ti+1=ti+2,xi+1=xi+2,yi+1=yi+2

(12)

ti+2=ti+3,xi+2=xi+3,yi+2=yi+3

(13)

代入式(9)、式(10)，即可得到动态障碍物今后某一时刻tn新的预测位置 (tn,xn,yn)

如图4所示，机器人运行过程中先后探测到位置为P0，P1，P2，P3动态障碍物，黑色实线轨迹f1(x) 为机器人依据探测到的障碍物位置P0，P1，P2预测的动态障碍物运动轨迹，P′3，P′4为机器人预测的后续两时刻动态障碍物的位置，当机器人探测到t3时刻实际位置P3的动态障碍物时，机器人根据动态障碍物的运动位置P1，P2，P3对其后续运行轨迹进行重新预测，图中浅灰色虚线便是重新预测后的轨迹曲线，P″4为基于新预测轨迹曲线计算获得的动态障碍物后续位置，由于P′3与P3存在偏差，因此预测出的后续节点P′4与P″4也存在偏差，机器人在每一个规划周期T，更新环境中的障碍物信息，迭代预测障碍物后续轨迹，并更新机器人的规划轨迹。

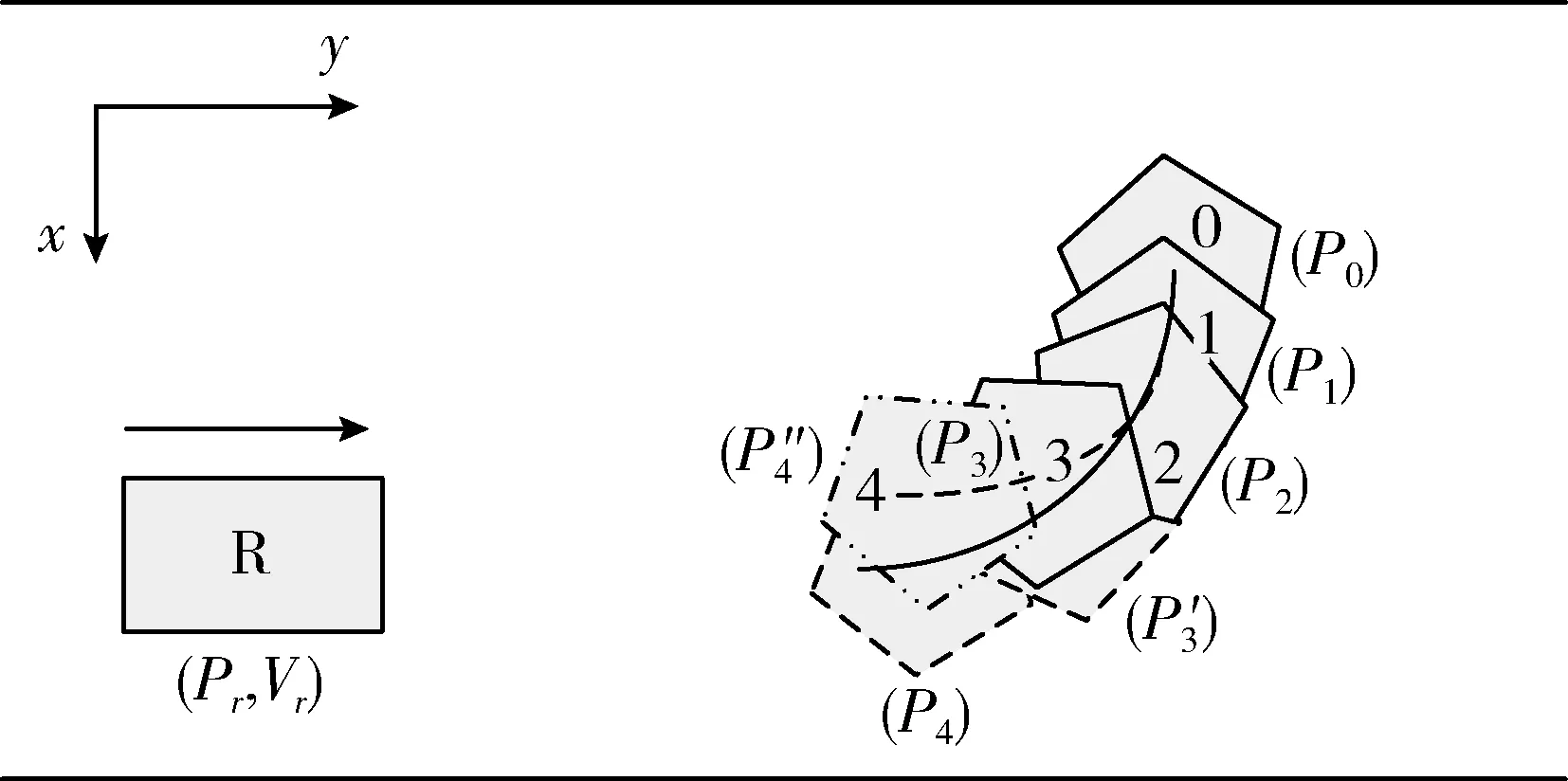
图4 动态障碍物运动预测

虽然环境中的运动目标在中长期内其运动具有很大的随机性，但在短期内的运动还是有一定规律可循。比如室外园区中常见动态障碍物如行人、车辆由于受到社会规则或其本身运动学模型的约束，其轨迹具有光滑性、连续性的特点，不会突然逆方向运动；或者即使有这种情况存在，但其概率也比较小。因此在一个较短时间内，通过构建拉格朗日运动预测模型，对园区动态障碍物的运动进行一定精度的预测是可行的。

2.3 基于改进D*lite算法的路径规划算法

在栅格地图中，设机器人当前节点为S，起始节点为sstart， 目标节点为sgoal， 动态障碍物的节点为O(O1,O2…On)。

栅格地图中的障碍物具有阻碍机器人通过的特性，我们称之为机器人通过该障碍物所占栅格的距离代价，用距离代价函数DisV(o) 表示，障碍物的距离代价值取相对较大的值进行表征。用下式表示

DisV(o)=K

(14)

为了避免机器人在避障运行时，规划出的路径离机器人距离太近，我们对障碍物进行适当的膨胀，膨胀后障碍物周边的栅格具有一定数值的距离代价，设栅格离障碍物之间的街区距离为Ro，膨胀区域为领域距离R，可得到障碍物周边栅格的距离代价函数如下式所示

(15)

通过障碍膨胀函数，可以对地图中的栅格逐一进行距离代价的计算，栅格地图中存在多个障碍物的情况下，每一个栅格取该栅格所有领域障碍物膨胀距离代价的最大值作为该栅格的距离代价值。障碍物膨胀如图5所示。

图5 障碍物膨胀建模

地图中任意两点间的路径可能有多条，地图中任意两个节点S1，S2之间的可行路径组成一个路径集，用dis(S1,S2) 表示路径集的距离代价。

与D*lite算法一致，当前节点s到目标节点sgoal的启发距离值为g(s)， 不同的是，令g(s) 为当前节点s到目标节点sgoal之间的最短路径加上节点s的距离代价。g(s) 计算公式如下式所示

(16)

当前节点s经过后继节点到达目标节点的路径代价为rhs(s)， 代表了s父节点的g(s)，rhs(s) 由下式表示

(17)

这里c(s,s′) 为s到节点s′的路径代价，当变量rhs(s)=g(s) 时，该节点处于一致状态，不需要更新；否则处于不一致状态，需要更新。

当前障碍节点是由机器人运行过程中实时探测得到，其置信度高；而障碍物后续运动轨迹是依据障碍物当前运动状态预测得到，因此其轨迹上的障碍物置信度较低。而且随着预测时间的增加，可信度将减小，将预测节点的距离代价函数定义如下

(18)

这里DisV(on) 表示障碍物节点o在时间n时的距离代价值，N表示预测步数范围。动态障碍物预测代价距离建模如图6所示。

图6 动态障碍物代价距离建模

基于动态障碍物运动趋势的改进D*lite避障路径规划算法流程如图7所示。

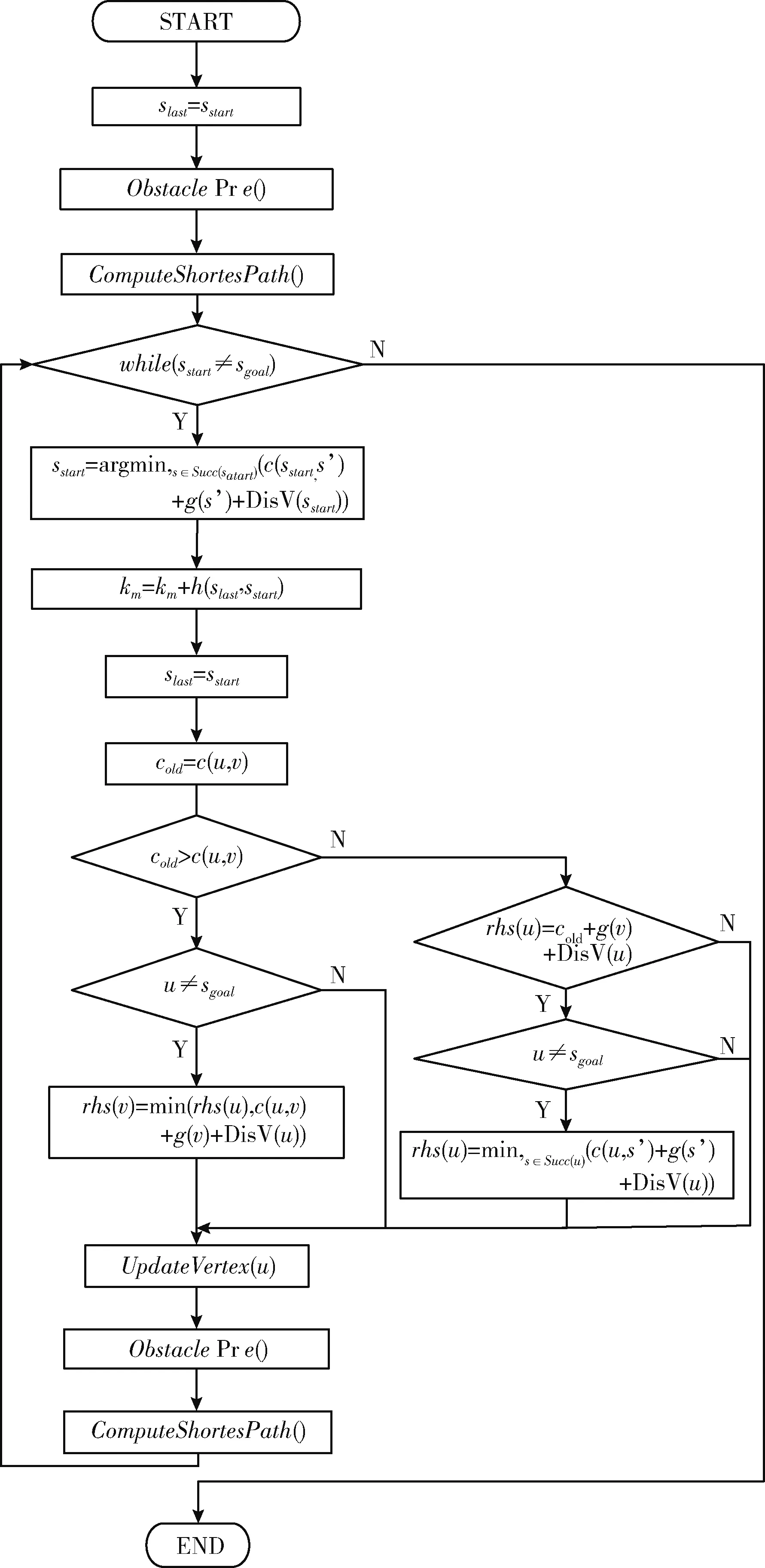
图7 改进D*lite算法流程

该算法中的计算最短路径的算法流程如图8所示。

图8 最短路径算法流程

3 仿真实验与验证

3.1 障碍物膨胀

仿真实验过程中， P(1,1) 灰色点代表机器人的起始点， P(30,30) 黑色点代表机器人下一个将要到达的目标点，图中黑色方块代表机器人运行过程中遇到的障碍物，为了使机器人避障过程中更安全，首先将障碍物进行合理的膨胀，实验过程中障碍物膨胀半径R=2， 图9(a)中的障碍物为机器人探测到的实际障碍物，中间图9(b)中灰色部分为障碍物的膨胀区域，图9(c)中障碍物为实际障碍物膨胀后变大的障碍物模型。障碍物膨胀后，本文对动态障碍物几种典型的运动进行了模拟验证，障碍物的膨胀过程如图9所示。

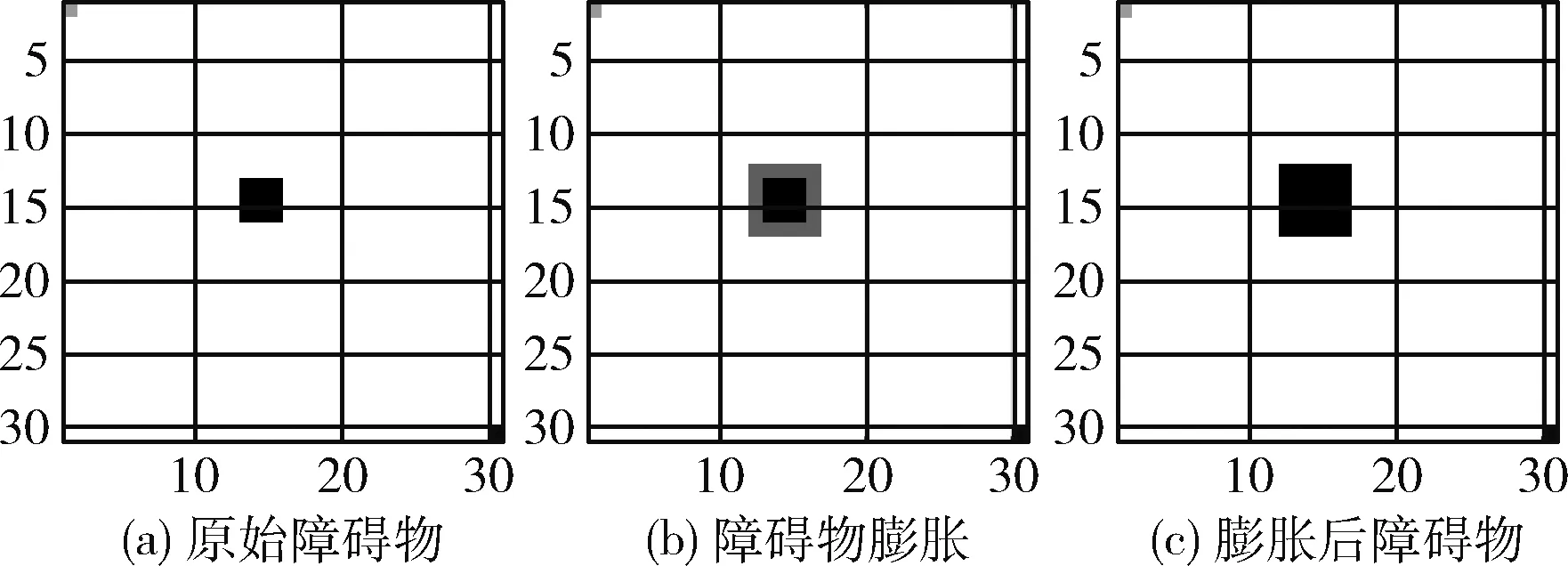
图9 障碍物膨胀

实验1，动态障碍物运动趋势如图10(a)所示，由黑色障碍物位置P(21,13) 向灰色障碍物位置P(11,23) 移动，图10(b)是障碍物移动的实际轨迹，图10(c)是机器人遇到图中的动态障碍物时，按照D*lite算法实时规划出的从机器人运动起始点到终点的路径，可以看出机器人在运行到点P(14,14) 时遇到障碍物，之后随着障碍物的运动，机器人一直处于动态避障状态，并计算代价最小的后续节点，但是由于机器人并不判断障碍物的后续运动位置，机器人会一直沿着障碍物的运动方向进行避障，直到障碍物停止运动(或者机器人超过或落后于障碍物)，机器人才可以完成障碍物避障，整个过程中机器人与障碍物的运动方向一致，且机器人速度大于障碍物时，机器人会从障碍物前方绕过，这样的避障方式会使发生碰撞的风险大大增大，整个避障过程经过的节点数为12。采用本文提出的方法进行动态障碍物避障，规划的避障路径如图10(d)所示，从图中可以看出，本文所提方法不仅考虑了障碍物当前的位置，而且会预测障碍物之后运动位置，当机器人遇到障碍物后，与机器人运动方向一致的避障方向代价增大，机器人会选择障碍物运动方向相反的路径进行避障，这样的避障方法更符合人类遇到障碍物的避障策略，根据障碍物的运动趋势，选择最优的方向与路径进行避障，提高避障安全性的同时，缩短避障的路径代价，整个避障过程机器人经过的节点数为9，经过的节点数相比D*lite算法减小25%。实验1的结果如图10所示。

图10 单障碍物与路径规划算法对比1

实验2，移动的机器人移动过程中，体积较小动态障碍物由黑色障碍物位置P(15，19) 移动到灰色障碍物位置P(24,7)， 移动机器人在运动到位置P(14,14) 时与动态障碍物相遇，进入避障区域，按照D*lite算法规划出的避障路径如图11(c)所示，可以看出随着障碍物的移动，移动机器人规划出的避障路径与机器人的运动方向相同，直到障碍物停止(或者机器人超过或落后于障碍物)，机器人完成避障，在整个运行过程中移动机器人一直与运动障碍物伴行，避障安全性无法保障，整个避障过程的节点数为14。本文所提算法规划出的避障路径如图11(d)所示，机器人遇到动态障碍物时，绕过运动障碍物，从运动障碍物的运动反方向进行避障运行，成功实现避障过程且可以大大提高机器人的避障安全性，整个避障过程的节点数为7，是D*lite算法避障节点数的50%，效率提高了一倍。实验2的结果如图11所示。

图11 单障碍物与路径规划算法对比2

实验3，移动机器人在运动过程中遇到多个动态障碍物(图中为两个障碍物)，图12(a)中稍大的障碍物由黑色障碍物位置P(8,13) 运动到灰色障碍物位置P(14,8)， 尺寸偏小的障碍物由黑色障碍物位置P(26,13) 移动到灰色障碍物位置P(19,24)， 在移动机器人向目标点运动过程中，基于D*lite避障算法如图12(c)所示，移动机器人首先在位置P(8,9) 遇到大障碍物，之后在位置P(23,11) 遇到小障碍物，机器人首先伴行大障碍物进行避障，绕或大障碍物后，在位置P(23,11) 遇到小障碍物，继续伴行小障碍物运行，直到绕过小障碍物，完成避障路径规划运行，整个避障过程中移动机器人避障移动的节点数为25。采用本文所提方法进行避障路径规划，如图12(d)所示，机器人基于动态障碍物的运动趋势进行障碍物位置预测，所规划出的避障路径沿大动态障碍物运动反方向，当机器人遇到小动态障碍物时，基于动态障碍物的运动趋势与移动机器人当前位置，规划出避障代价较小的路径实现了动态避障，整个避障过程的安全性大大提高，并且避障经过的路径节点减小到14，相比D*lite算法，避障节点数减少44%。实验3的结果如图12所示。

图12 多障碍物与路径规划算法对比

另外值得注意的是，基于本文算法在避障过程中显示的障碍物不完全是实际的障碍物，也可能是避障时算法预测的障碍物未来出现的位置，例如最后一个实验中机器人遇到第二个障碍物实际上是算法对障碍物的预测位置。

3.2 实验结果对比

从以上仿真实验结果可以看出，在移动机器人遇到图10、图11中的单动态障碍物时，采用本文提出的改进算法相比D*lite算法其避障代价分别降低了25%和50%，而且所规划出的避障路径均与动态障碍物运动方向相反，当机器人遇到图12中的多动态障碍物时，采用本文所提算法，避障代价减少了44%，而且与动态障碍物的重合路径大幅减少。移动机器人采用本文所提方法对比D*lite方法对于动态障碍物的避障无论从避障安全性还是避障效率上均有显著提升。

4 结束语

本文提出了移动机器人基于动态障碍物运动趋势的改进D*lite避障路径规划算法，采用了类似人在进行动态障碍物避障类似的策略，提出了基于动态障碍物历史轨迹的运动预测算法，优化了D*lite算法在障碍物避障时只考虑当前状态，不考虑运动趋势的问题，建立了预测障碍物运动位置代价函数模型，改进了D*lite算法，实现了机器人基于动态障碍物运动预测的避障路径规划。通过搭建仿真环境，选择典型的单动态障碍物、多动态障碍物场景进行仿真验证，实验结果显示本文所提算法在进行动态障碍物避障路径规划时，无论避障的效率还是避障的安全性均比D*lite算法有显著提升。