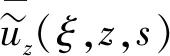层理泥质白云岩各向同性弹性力学试验研究

谢财进，饶军应，刘灯凯，聂崇欣

(贵州大学 土木工程学院， 贵州 贵阳 550025)

0 引言

层理泥质白云岩在西南地区许多隧洞及地下工程中大量赋存，而层状岩体常常会表现出各向同性特征，特点为水平方向与垂直方向上力学特性不同，对围岩变形、应力大小有显著影响[1-5]。岩石力学性能研究的方法主要有数值分析和试验研究。

在数值分析方面，潘睿等[6]基于能量分析法，对层状岩石的各向同性水平和垂直层理方向的断裂差异开展研究，对优选射孔位置和施工排量、提高压裂的增产效果具有参考意义。刘运思等[7]指出岩体各向同性体力学特性在不同的层面倾角下存在较大的差异，基于Helmholtz自由能与不可逆热力学的基本原理，对其体积模量和剪切模量与层面倾角的函数关系式、内时损伤本构方程开展研究，描述损伤发生前后的变形特点，有效地反映各向同性岩体的非线性和剪胀扩容等物理力学现象。谢云跃等[8]通过将层状岩体开展单轴压缩数值试验结果与岩体各向同性弹塑性本构模型嵌入ABAQUS计算结果对比分析，同时将该模型退化为各向同性模型应用于层状岩体地下工程的计算，计算结果均能验证该模型的有效性和实用性。这类研究仅对岩石宏观力学性能开展分析，未从岩石微观上解释其各向同性存在的本质原因以及与宏观力学间的联系。

在试验研究方面，李江腾等[9]对不同层理角度的板岩开展单轴压缩试验和双扭常位移松弛试验，分析板岩试件层理角度与其抗压强度及断裂韧度的相关规律。张东明等[10]基于改进后的Duncan模型，建立单轴损伤破坏模型,通过对含层理及均质岩石试件开展单轴压缩实验、CT层析扫描测试，研究层理岩石破坏特征及损伤演化过程中的声发射参数特征、能量耗散与传递规律。已有学者将岩石的微观与宏观结合考虑，但仅仅停留于岩石微观表象分析，未能从岩石微观矿物组成对岩石结构影响入手。

本文对层理主控泥质白云岩开展能谱分析试验(EDS试验)，对其微观结构及其矿物组分开展分析，证明其具有各项同性，最后结合单轴压缩试验对其宏观力学性能开展研究，建立弹性本构方程、动力问题运动平衡微分方程，对不同层理角度下泥质白云岩的各向同性力学性能开展研究。

1 层理泥质白云岩各向同性研究

为研究层理泥质白云岩晶体特性，对其开展能谱分析试验(EDS试验)。由于晶态物质成分、结构不同，使得能谱曲线的脉冲峰数目、形状、排列等不同。通过能谱曲线对晶体所含矿物成分进行分析，进而完成样品成分的定量分析[11-13]。

试验仪器采用德国卡尔·蔡司∑IGMA扫描电子显微镜带能谱仪(EDS)，试验原理为：X光量子从Si(li)探测器接收信息后给出电脉冲讯号，这种讯号经放大器放大整形，再送入多道脉冲分析器，最后在仪器的显像管上将脉冲数—脉冲高度曲线显示出来，得到X光量子的能谱曲线，试验步骤不再赘述。通过EDS试验，获得层理泥质白云岩的物质成分谱图，如图1～图4所示。

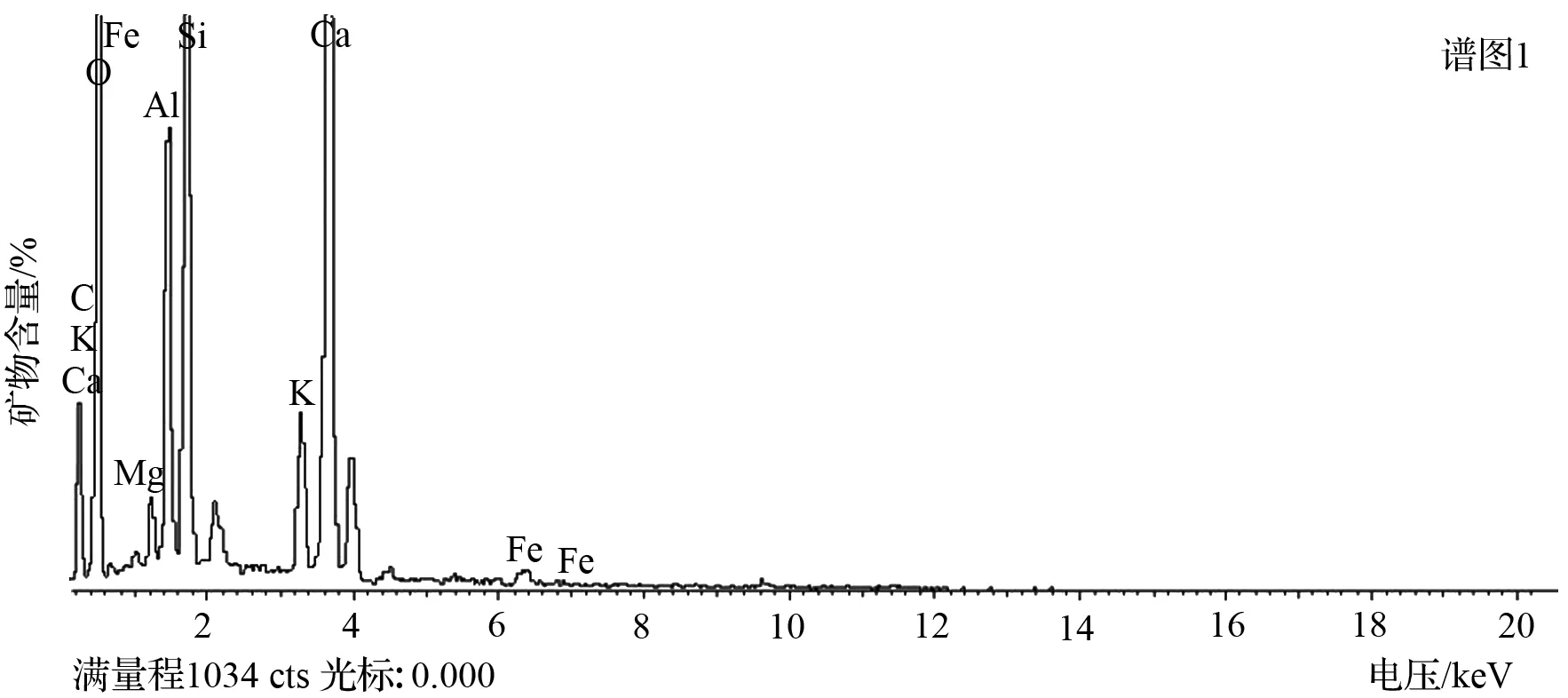
图1 样品A10谱图Fig.1 Spectrogram of sample A10

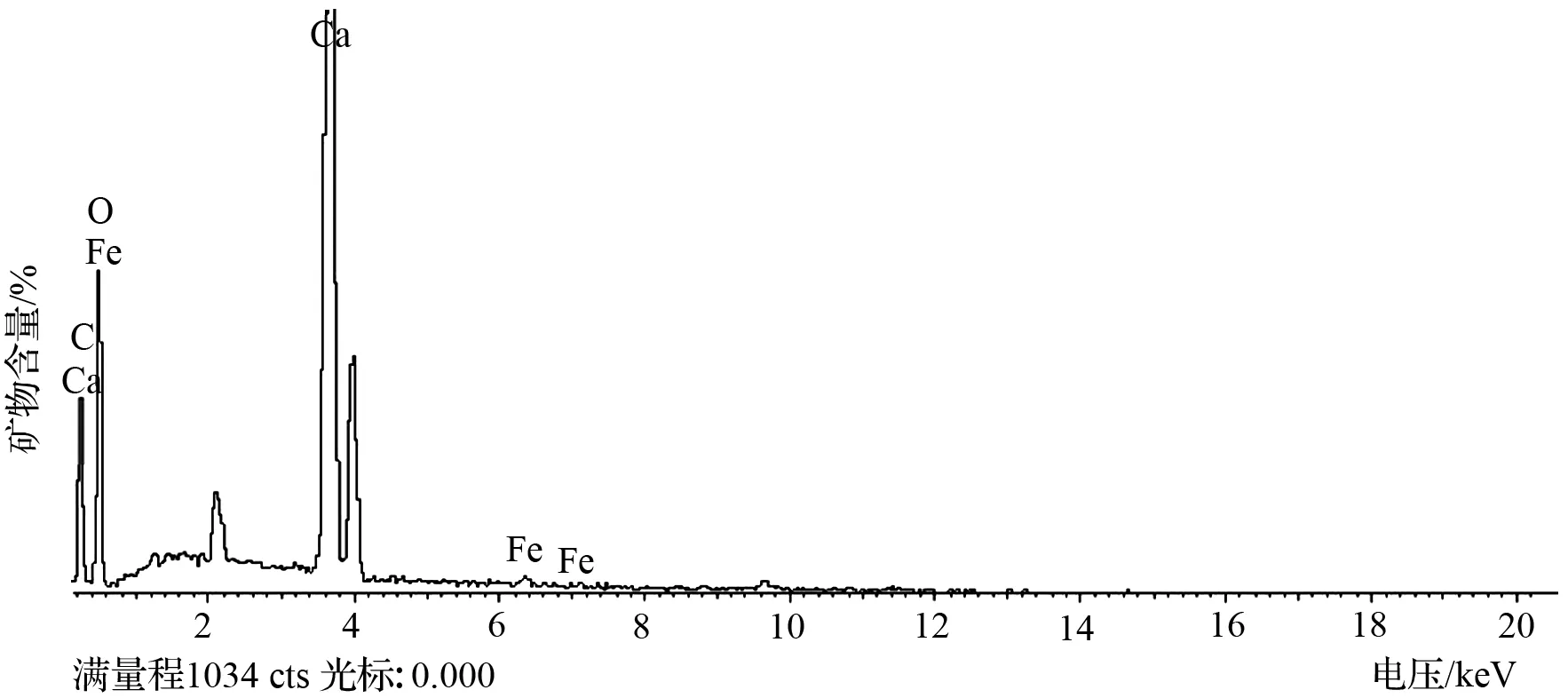
图2 样品B4谱图Fig.2 Spectrogram of sample B4

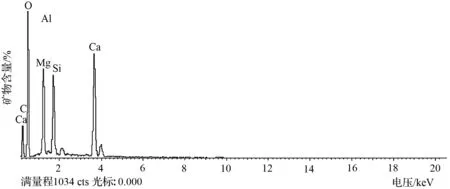
图3 样品D7谱图Fig.3 Spectrogram of sample D7

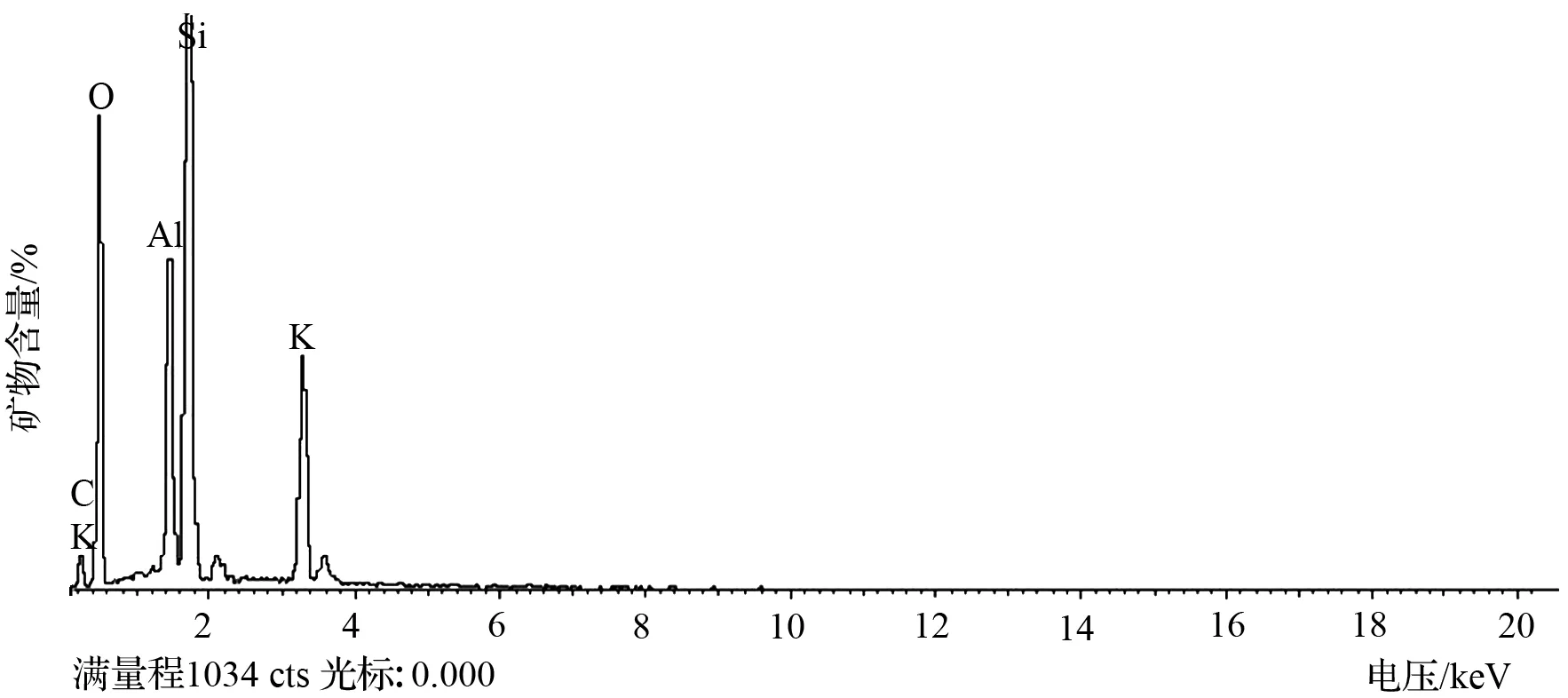
图4 样品F11谱图Fig.4 Spectrogram of sample F11

能谱分析的结果显示，层理泥质白云岩含有大量Ca、Si、Mg、Al等元素，其矿物组成基本一致，但由于各种矿物含量不同导致其微观结构差异化。根据泥质岩体物质成分对比分析可知，层理泥质白云岩中主要成分为石英、白云母、斜绿泥石等。研究表明，层理泥质白云岩中石英晶体的长轴与白云母、斜绿泥石的片状结合呈层状排布，结构有明显的定向排列特征，单晶体结构相互组合、叠聚将导致片状叠聚物在水平方向与垂直方向上力学特性不同，使其具有各向同性的力学特性。该特征将为层理泥质白云岩弹性力学本构模型的建立提供基础。泥质白云岩微观结构图如图5所示。

图5 泥质白云岩微观结构图Fig.5 Microstructure of argillaceous dolomite

2 岩体各向同性弹性本构方程

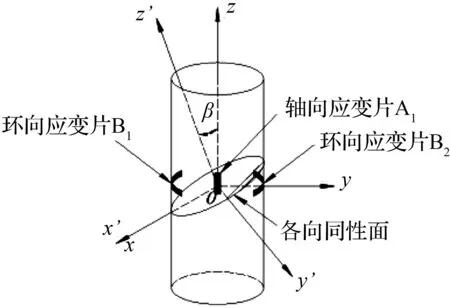
将试验岩样制成直径50 mm，高100 mm的圆柱体，岩样中存在一个各向同性面x′oy′以及与之垂直的旋转主轴z′，建立x′oy′z′坐标系，将y′oz′平面绕x′轴旋转β角后得到新坐标系xoyz，如图6所示。

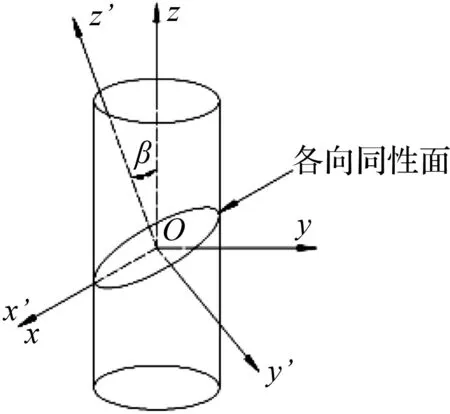
图6 层理泥质白云岩整体与局部坐标系Fig.6 Integral and local coordinate systems of the shale dolomite

层理泥质白云岩弹性部分应变增量为应力增量的线性函数，基于GUATAUM等[14]对科罗拉多页岩各向同性弹性本构方程研究，得出局部坐标系x′oy′z′下层理泥质白云岩各向同性弹性本构方程为：

(1)

式中：Δε为正应变增量；Δγ为切应变增量；Eh为平行于各向同性平面弹性模量；Ev为垂直于各向同性平面弹性模量；νhh为平行于各向同性平面内泊松比；νvh为垂直于各向同性平面内泊松比；Gvh为垂直于各向同性平面剪切模量；Δσ为应力增量；Δτ为切应力增量。

另外，岩体各向同性的5个弹性常数有如下热动力学约束：

Eh,Ev,Gvh>0,

(2)

-1≤νHH≤1,

(3)

(4)

5个弹性常数一般都是独立存在的无理论关系，但Saint-Venant经研究发现得出5个常数间的经验公式[15]：

(5)

由于应变能不随坐标系变化而变化，基于张学民等[16-17]转轴位移分量的变换关系，整体坐标系xoyz下的本构方程可由式(1)通过应力、应变和柔度张量变化得到：

(6)

式中:系数Aij与弹性常数Eh、Ev、νvh、νhh、Gvh的关系见参考文献[7]。

3 岩体各向同性弹性常数试验研究

试验岩样取自贵阳市轨道交通火车站站～沙冲路站区间隧道。岩样埋深40 m，取样角度(β)为0°、15°、30°、45°、60°、90°(图7)，采用岩石钻芯机取样。岩样经切割、打磨制作成直径50 mm，高100 mm的圆柱体(图8)，共25个，试验岩样的几何尺寸见表1。岩样两端面不平行度误差不大于0.05 mm；沿岩样高度、直径的误差不大于0.3 mm；端面垂直于岩样轴线，偏差不大于0.25°。

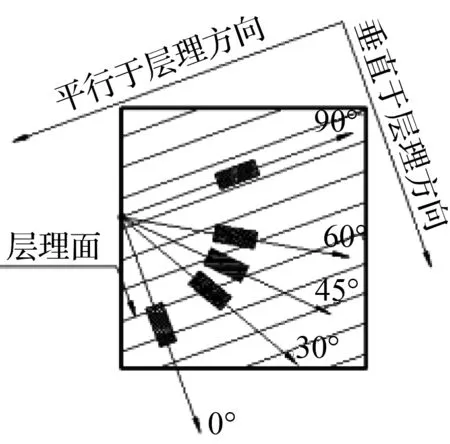
图7 岩石样本钻取方向示意图Fig.7 Drilling direction of rock sample

(a) 钻芯岩样

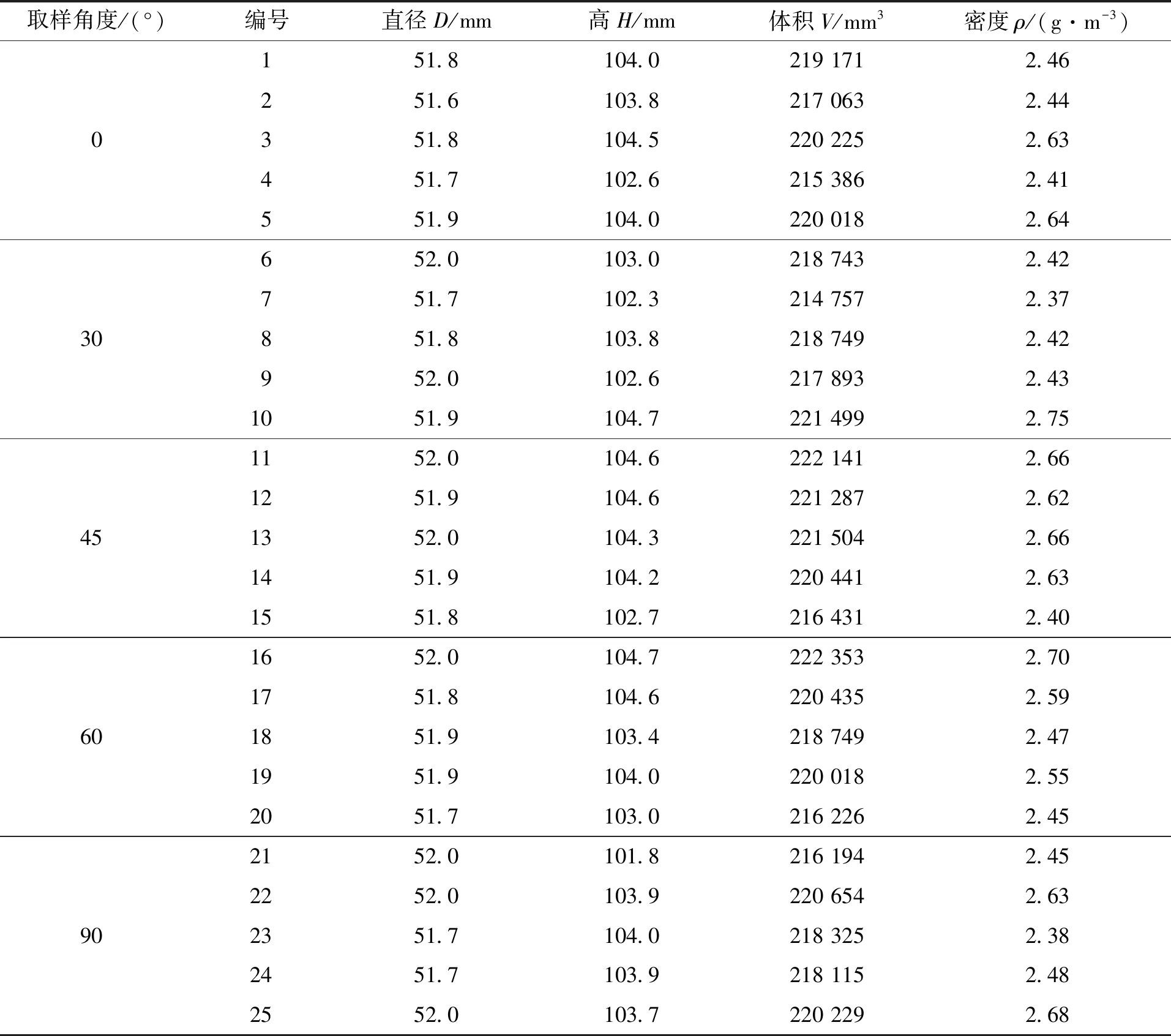
表1 层理泥质白云岩单轴压缩试验岩样几何尺寸Tab.1 Geometric dimensions of rock samples for uniaxial compression test of argillaceous dolomite

岩样应变采用静态电阻应变仪进行测试，在岩样上粘贴A1、A2、B1、B2应变片，共4片(图9)，A应变片测圆柱体轴向应变εz，B应变片测圆柱体环向应变εy。在全数控电液伺服力学压力机与静态电阻应变仪共同作用，测得岩样的材料强度及变形大小。

(a) 侧视图

3.1 弹性常数关系式

采用单轴压缩试验测定各向同性岩石材料强度和变形特征。对不同层理角度的层理泥质白云岩，仅在轴向(z方向)施加压力σz，假定岩样内部的应力、应变均匀分布，根据式(1)、式(6)将其应力、应变的关系简化为：

(7)

式(7)中，A13、A23、A33、A53为柔度矩阵中的元素，其分别为：

(8)

(9)

(10)

。

(11)

当岩体由各向异性退化为各向同性弹性体后，其独立弹性参数由9个变为5个，分别为Eh、Ev、νvh、νhh、Gvh。其中，弹性模量视为由单轴压缩试验得到的应力应变曲线在σmax/2(σmax岩样破坏最大应力值)处直线段的斜率，即：

(12)

视泊松比ν为：

(13)

当β=0°时，代入式(12)、式(13)得：

(14)

(15)

当β=90°时，代入式(12)得：

(16)

(17)

由式(14)、式(15)、式(16)将独立常数Ev、νvh、Eh求出。νhh、Gvh需建立另外一组取样角度的岩样方程与式(17)联立求解。故仅需3种不同倾角的岩样，便可通过单轴压缩试验获得层理泥质白云岩各向同性的5个独立常数。

3.2 弹性常数的测定

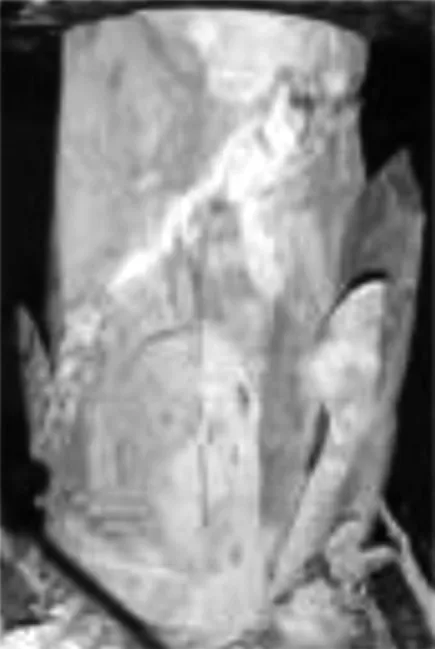
通过对5个不同取样角度岩样开展单轴压缩试验，发现：0°组试件破坏形态完整，试件表面成块脱落；30°组试件破坏形态完整，有一部分沿着试件表面裂缝破坏，试件顶部呈现锥形破坏形态；45°组试件破坏形态较为完整，沿着试件45°斜面裂开；60°组试件外部破坏形态细碎，而试件中间破坏比较完整，试件顶部呈现锥形破坏形态；90°组试件破坏后呈现条状，试件沿着加载方向破坏，破坏后较完整(图10)。

0°

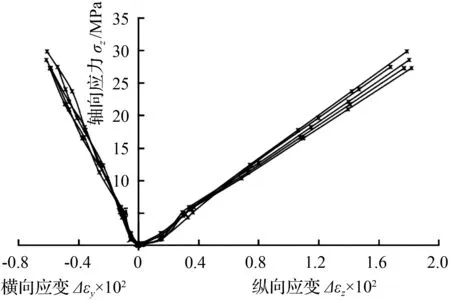
基于单轴压缩试验结果，绘制不同取样角度下的轴向应力—横向应变、轴向应力—纵向应变图(图11)。其应力应变曲线可大致分为两个阶段：第一阶段，加载开始到峰值破坏应力和最大应变的1/3处，应力应变曲线呈下凹状，属于岩体压密阶段，随着轴向荷载增加岩样内部的空隙、裂纹闭合，逐渐接近弹性体材料；第二阶段，岩样内部的空隙、裂纹完全闭合，应力应变曲线呈一次函数，属于线弹性阶段。

(a) 取样角度β=0°

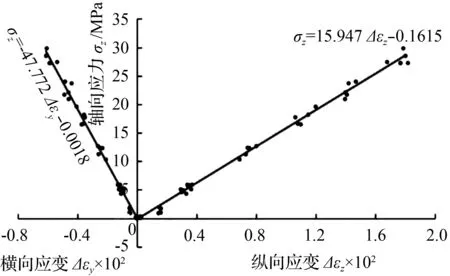
基于单轴压缩试验结果，对β不同的5组岩样应力应变分别进行线性拟合，岩样单轴抗压强度与应变值满足下列关系：

(18)

式(18)中：A、B、C、D为应力应变拟合系数。拟合曲线如图12所示。β不同的5组岩样应力应变线性拟合关系式见表2。

(a) 取样角度β=0°

表2 不同β角度岩样应力应变线性拟合关系式Tab.2 Linear fitting formula of stress and strain for rock samples with different β angles

基于线性拟合结果，可计算出不同β下岩样的视弹性模量E和视泊松比ν(表3)。由式(14)、式(15)、式(16)可得4个弹性常数Ev=15.95 MPa、Eh=14.48 MPa、νhh=0.24、νvh=0.31。另外，随取样角度不同，E、ν也不相同。

表3 不同β岩样视弹性模量E和视泊松比νTab.3 Apparent elastic modulus E and apparent poisson’s ratio ν of different rock samples β

将表3中岩样的数据代入式(12)中，得3个取样角度下弹性常数Gvh(表4)，取其平均值作为层理泥质白云岩弹性常数，Gvh=6.21 GPa。

表4 岩样弹性常数GvhTab.4 Elastic constant of rock sample Gvh

3.3 岩体各向同性弹性体动力问题

针对城市地铁隧道，为更好表征城市路面荷载对围岩扰动的力学行为，考虑具有各向同性的泥质白云岩在冲击荷载作用下的动力响应，从各向同性弹性轴对称空间动力问题出发，利用积分变换，建立各向同性层理泥质白云岩结构的解析刚度矩阵，进而分析外部荷载对隧道围岩的影响。基于鲁巍巍等[18]对各向同性弹性体轴对称动力问题运动平衡微分方程的研究，可得：

(19)

式(19)中：r、z分别为径向距离和竖向距离；t为时间变量；ur、uz分别为径向位移和竖向位移；σr、σθ、σz分别为径向应力、环向应力和竖向应力；τzr为剪应力。

几何方程：

(20)

各向同性弹性体的应力、应变关系式为：

(21)

联立式(19)、式(20)、式(21)，得位移表示层理泥质白云岩弹性体空间轴对称动力问题的控制方程：

(22)

对式(22)进行Laplace及Hankel变换后得：

(23)

式(23)中：ξ为Hankel转换常量；s为Laplace转换常量；ρ为岩体密度，泥质白云岩密度取各岩样密度平均值ρ=2.53 g/cm3。

(24)

式(24)中：

可得其通解为：

(25)

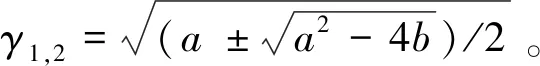
代入数据后得：

a=2.72ξ2-534.74s2,

(26)

b=0.92ξ4-501.52ξ2·s2+51874.22s4,

(27)

(28)

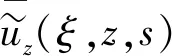
4 结论

本文基于岩体各向同性弹性本构方程、轴对称动力问题运动平衡微分方程，通过对层理泥质白云岩开展各向同性弹性力学试验、EDS试验研究，得出如下结论：

① 能谱分析显示，层理泥质白云岩的矿物组成基本一致，造成层理泥质白云岩微观结构的差异化的主要原因是各类矿物含量的不同。其主要成分为石英、白云母、斜绿泥石等，3种成分的晶体结构都会造成岩体微观力学各向异性。但当这些晶体结构相互组合、叠聚后，石英晶体的长轴会与白云母、斜绿泥石的片状结合呈层状排布，会使岩体力学特性发生改变，使其由单晶体的各向异性变为微观结构的各向同性。

② 层理泥质白云岩中石英晶体的长轴与白云母、斜绿泥石的片状结合呈层状排布，结构有明显的定向排列特征，单晶体结构相互组合、叠聚将导致片状叠聚物在水平方向与垂直方向上力学特性不同，使其具有各向同性的力学特性。该特征将为层理泥质白云岩弹性力学本构模型的建立提供基础。

③ 构建层理泥质白云岩各向同性弹性本构方程，通过开展单轴压缩试验获得不同取样角度下的岩体力学参数，进而得到岩体各向同性的5个弹性常数Ev=15.95 MPa、Eh=14.48 MPa、νhh=0.24、νvh=0.31、Gvh=6.21 GPa。