立足“三核”的小学数学单元整体教学探究
——以人教版六年级下册《圆柱与圆锥》单元教学为例
2021-01-20
(集美区实验小学,福建 厦门 361022)
一个人的核心素养,常常体现为面对新情境、新问题时所表现出来的品格和能力,而这些品格与能力的形成,需要教师整体把握小学数学课程,在整体视角下开展教学实践与研究。[1]开展单元整体教学研究,是发展学生品格和能力的有效举措。单元整体教学更多的是从分解知识点、挖掘知识关联、重构单元知识体系入手进行研究。本研究是指教师以小学数学教材中的单元为整体,展开系统化、科学化的教学设计、教学实施。[2]它要求教师从整体上把握单元教学内容,对单元教学内容进行完全的解读、分析、调整、重组、整合、优化后,形成单元核心知识;根据核心知识和学情设计单元教学核心环节,让学生感悟核心思想,发展核心素养。不仅着眼于单元知识的关联,更侧重于挖掘单元知识体系所蕴含的思想方法,以核心教学活动促进学生核心素养的发展。下面以人教版六年级下册第二单元《圆柱与圆锥》为例,探讨立足“三核”(核心知识、核心环节、核心思想)的单元整体教学。
一、统整核心知识——用心解读教材,确定教学主线
核心知识是每个教学活动中,必须要让学生掌握、理解、探究的主要知识技能,是一个学期教学、一个单元教学、一节课教学的主体内容与知识主干,是整个教学活动链条中的关键环节,是联系全部教学活动的轴心,是教学活动之魂的栖息地。[3]核心知识及其之间的关系,蕴含着反映学科本质的基本特征,这些特征往往反映学科的基本思想,是学生理解所学内容的本质和发展学科核心素养的关键。因此,教学前,教师最重要的工作是解读、分析教材,统整单元核心知识。在“圆柱与圆锥”单元教学中,圆柱和圆锥包含的知识块有圆柱的特征、表面积和体积,圆锥的特征和体积;圆柱的特征是学习圆柱其他知识的基础,如图1 所示。圆柱的特征是根本,理解掌握其特征,圆柱和圆锥的侧面积、表面积、体积、切面面积等相关知识的问题便迎刃而解。
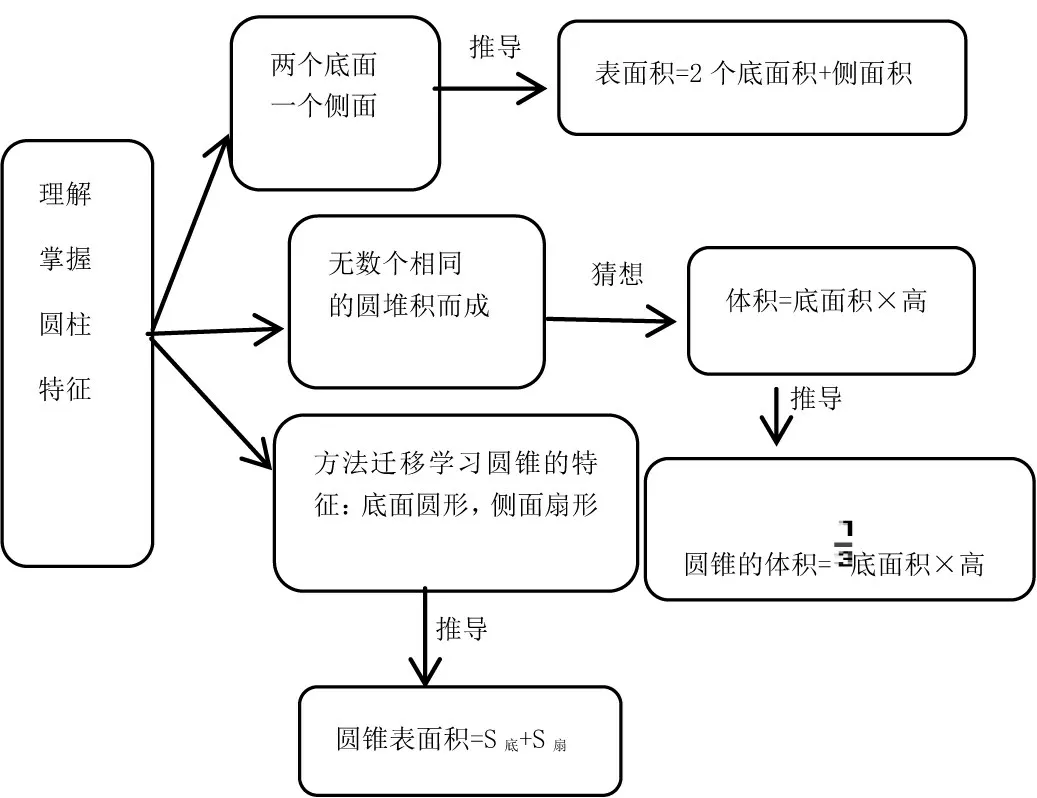
图1 圆柱特征与圆柱其他知识的关系
综上,根据小学生的认知特点,可将本单元的教学主线确定如下(表1):
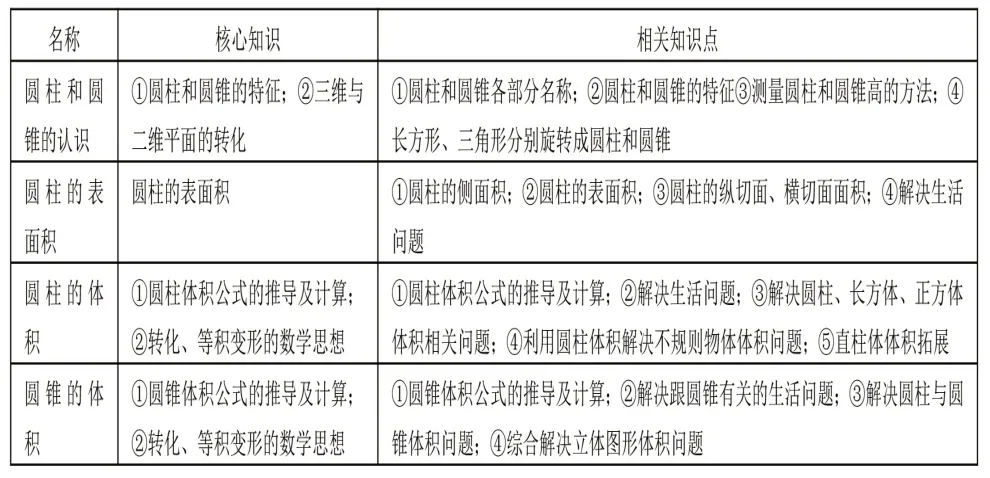
表1 《圆柱和圆锥》单元核心知识
二、紧扣核心环节——双向联结沟通,促进整体建构
教学实施的核心环节是教学策略。《义务教育数学课程标准(2011 年版)》指出:教材编写应当体现整体性,注重突出核心内容,注重内容之间的相互联系,注重体现学生学习的整体性。[4]这就意味着教师在整体感知教材的基础上,在进行单元教学环节设计与实施时,要注重呈现不同数学知识之间的关联,要注意教学策略和教学方法的选择,帮助学生理解知识之间的逻辑顺序以及实质性联系,展示数学知识的整体性和数学方法的一般性。
(一)横向联结
知识之间的联系有横向联系和纵向联系。教学时,教师不仅要引导学生对知识点进行联结,从整体上建构数学知识的教学环节,更要引导学生进行学习方法、学习经验的横向联结,促进学习方法的迁移与运用。如教学“圆柱和圆锥”的相关知识时,可引导学生从“七个维度”[5],运用画图、列式、推理等方法进行横向比较(比较的内容可根据教学的进度逐项对比增加),如图2 所示。

图2 从七个维度对比学习圆柱、圆锥知识的方法
以“体积”的教学为例,圆柱和圆锥都通过等积变换实现体积公式的推导过程。圆柱的体积可以转化为等体积的长方体的体积进行计算,也可以想象成若干个相等的圆的面积的叠加;圆锥的体积可以转化为与它等底等高的圆柱进行计算,通过实验,发现它的体积是与它等底等高圆柱体积的三分之一。又如“特征”的教学,圆柱和圆锥是三维图形,对三维图形的认识,关键在于将三维图形表示在二维平面上,二维与三维之间的转换是学生空间观念形成的重要方面。如图2 所示,两者在特征的教学上,都是通过展开与折叠、视图与还原、切截与叠加、旋转等维度实现立体图形与平面图形之间的转换,有助于培养学生的空间想象能力和推理能力。教学时,教师要有意识地引导学生进行方法的对比和联结,让学生在比较中掌握几何的数学学习方法,积累数学活动经验。
(二)纵向深入
在单元整体教学设计和实施过程中,教师不仅要引导学生对知识、方法进行横向建构,也要进行纵向深入学习。小学阶段立体图形的学习只有两个单元,分别是五年级下册“长方体和正方体”单元和六年级下册“圆柱和圆锥”单元。教师可从知识的纵向联系角度,引导学生比较学习(表2):
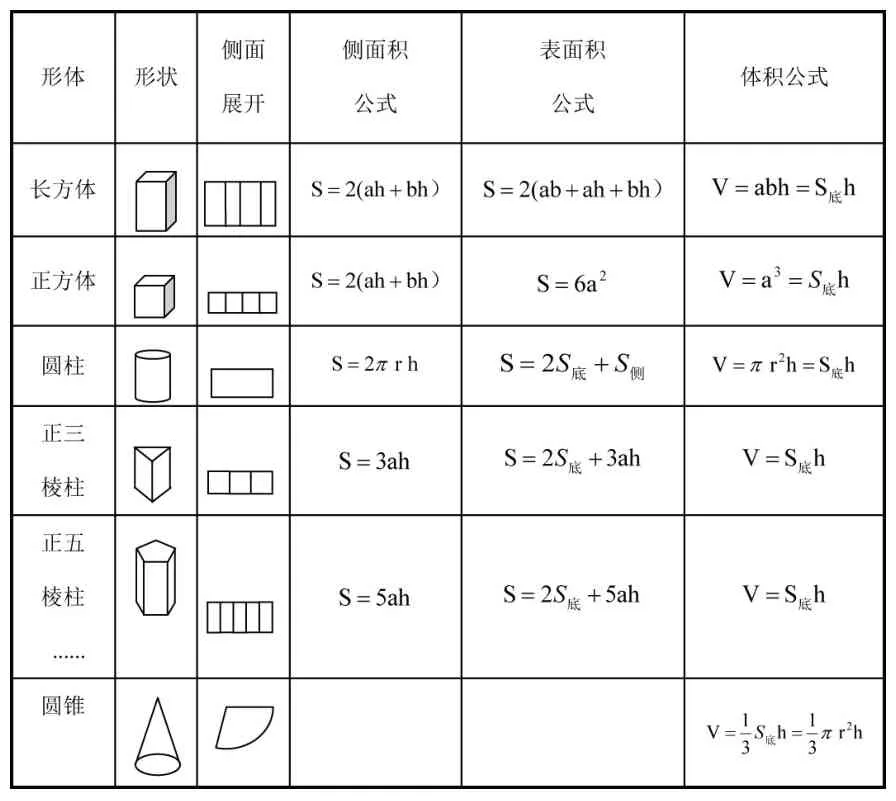
表2 立体图形纵向联系对比
教师立足于立体图形的知识体系,瞻前顾后,引导学生进行知识的联结和建构。“瞻前”即回顾五年级学习的长方体和正方体的相关知识,“顾后”即在学习长方体、正方体、圆柱体和圆锥体的基础上,拓展学习三棱柱、五棱柱等直柱体的表面积和体积。通过实验、观察、比较等,发现所有直柱体的侧面积都是“底面周长×高”(图3),表面积都是“侧面积+两个底面面积”,体积都是“底面积×高”(图4),从而形成良好的认知结构。
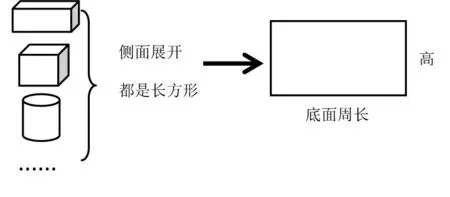
图3 直柱体侧面展开图
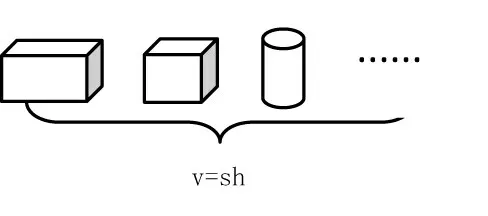
图4 直柱体体积公式
三、渗透核心思想——丰富数学实践,发展核心素养
数学核心素养包含数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析等六个方面。圆柱与圆锥,属于图形与几何领域,这部分教学是以发展学生的空间观念、几何直观、推理能力为核心。苏霍姆林斯基说过:“儿童的智慧在他的手指尖上。”“圆柱与圆锥”单元教学中涉及到各种操作活动,如切、卷、转、涂、挖、变形等,教材中没有安排专门的例题,但在课后习题中有所涉及。为促进学生深度学习,应充分开展数学活动,渗透化曲为直、等积变形、转化、化曲面为平面等思想方法,让学生在活动中掌握知识,发展核心素养。
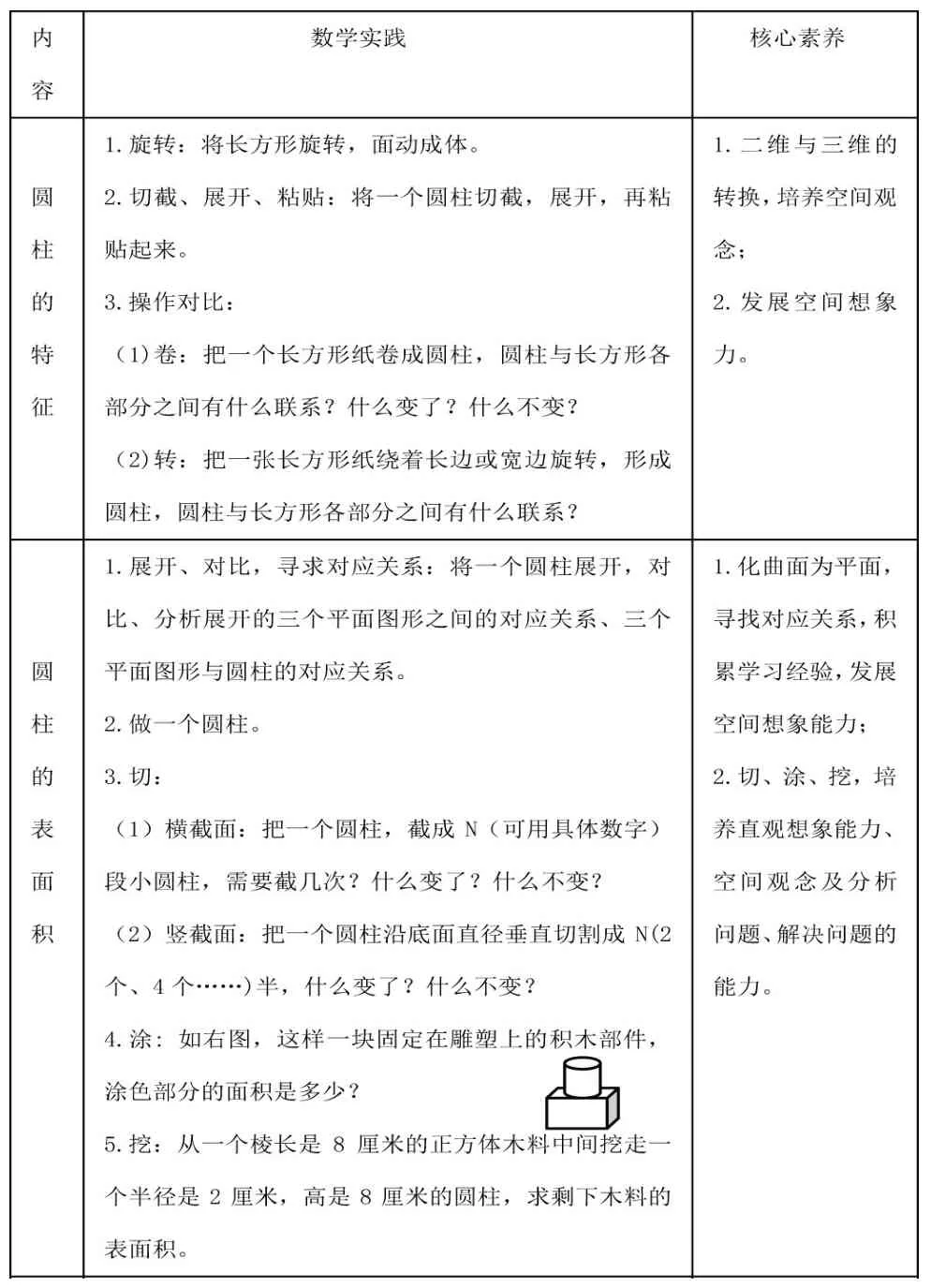
表3 《圆柱和圆锥》单元实践活动安排

(续上表)
总之,单元整体教学,教师要从整体上把握教材体系,解析教材,提炼核心知识;在核心教学环节,设计多向教学活动,引导学生主动建构,从整体上理解知识体系,掌握学习方法,积累学习经验;根据知识和学生思维特点,进行拓展、变式、操作等数学实践活动,让学生在实践中思考,在思考中提升,发展数学核心素养。
