应急条件下轻型、快速架设桥梁结构探讨

张立乾 陈红 闫晶 李兵 吴星

(北京特种工程设计研究院 100028)

引言

轻型、快速架设桥梁在很多情况下是必要的, 比如抢险、应急等。传统索道桥一般采取缆索密间距分布的布置方式, 这种布置方式存在横向稳定性不足、桥面系架设周期过长等诸多不利因素。为了克服背景技术的不足, 同时面向轻型、快速架设的桥梁功能, 本文提出了一种新型的桥梁结构型式, 并结合工程案例, 基于有限元计算软件进行数值计算, 按照从整体到局部的原则验证了整体结构的科学合理性, 以期给同类工程提供更优的解决方案。

1 结构体系设计

以某应急桥梁为例, 摒弃传统索道桥缆索密间距分布的布置方式, 采用两个主缆作为主承载构件, 横梁采取了轻型化的结构型式, 和主缆连接的构件采用了专用倒U 型固定装置, 桥面承载板采取轻型纵横正交的薄壁竖板构成的密间距梁格系, 并设置了模块化桥梁配重。

1.1 主缆

该应急桥用于连接跨越山谷的两个隧道, 桥型布置如图1 所示。以分布在桥面两个边侧的具有较高初始预张力的主缆作为全桥主要承载构件, 中间不再设置分布缆索。主缆采用1860 级平行钢丝束, 外包双层挤压高密度聚乙烯防腐材料, 外径118mm, 断裂极限强度为11670kN。主缆成桥态垂度1.74m, 主跨跨径70m, 垂跨比1/40。活载为特载车, 全重78t, 6 轴, 轴距从前至后依次为2m、4m、2m、2m、2m, 轮距2.5m,最大爬坡能力为30%。主缆通过索鞍锚固于锚座后部, 锚座通过植根于岩层的预应力锚索提供给主缆锚固抗力。主缆横向间距5m。

1.2 横梁及端部固定装置

横梁采取高强铝合金闭口小箱梁, 采用6061AL 高强合金铝材料, 目的是减低自重的同时又保证必要的结构刚度和强度。间距400mm设计加劲肋板。横梁端部设置倒U 型固定装置,中部为倒U 型固定部分, 实现横梁和主缆可靠的扣接,端部为锁定部分, 实现横梁和主缆的锁止, 防止横梁沿主缆滑移。倒U 型固定装置顶部还设有两侧伸出的端臂,其作用有两个: 一是端壁之间距离为1000mm, 横梁安装间距即为1000mm, 这样横梁安装就位时, 可以发挥卡尺的作用; 二是前后两个相邻的端壁之间相接处设有扣件,实现相邻横梁的顶紧扣死。横梁布置见图2 所示, 固定装置见图3。一道横梁包含两个端部固定装置总质量为200kg。

图1 桥型布置Fig.1 Bridge layout

图2 横梁布置(单位: mm)Fig.2 Layout of cross beams(unit: mm)

图3 横梁固定装置(单位: mm)Fig.3 Cross and longitudinal layout of cross beam fixing device(unit: mm)

1.3 桥面承载板

桥面承载板采取纵横正交的薄壁竖板构成的密间距梁格体系, 在强度、刚度满足的条件下进一步降低自重,同时密间距梁格体系可以给其上车辆的轮胎提供较好的“抓地力”。单品桥面承载板全 宽 566mm、长 3990mm,纵向由11 道间距50mm 的高70mm、厚6mm 的纵向肋板构成, 横向由间距100mm 的高40mm、宽4mm 的隔板构成, 纵横钢板采用焊接连接或一次脱模成型。材料采用Q420 高强度结构钢。纵向肋板间距1000mm 设有凹槽, 用于卡住其下的横梁顶板, 防止桥面承载板和横梁的纵向相对滑移; 同时在横梁顶部设置有净间距572mm 的桥面承载板的横向卡槽, 防止桥面承载板和横梁的横向相对滑移; 横梁顶部卡槽顶部设有下压扣件, 扣住桥面承载板的边肋顶面, 防止桥面承载板和横梁的垂向脱空。桥面承载板布置见图4。一品桥梁承载板(4m 长, 0.566m 宽)总质量为171kg。

图4 桥面承载板布置(单位: mm)Fig.4 Layout of bridge deck bearing plate(unit: mm)

1.4 桥梁配重

为控制主缆受荷特别是在较重车辆通过时的线形, 设置了搬运方便快捷的模块化设计的桥梁配重, 可以实现快速布设。配重采用铸铁块, 单块尺寸1000mm(长)×151mm(宽)×140mm(高),质量166kg。桥面对称每侧设置三组, 置于最外侧的桥面承载板上。配重通过上、下卡板和竖向螺杆固定于桥面承载板上, 如图5 所示。桥面每侧3 块配重, 横向共计6 块配重, 可实现全桥1000kg/m 的配重。

桥梁单件最大重量200kg, 4个熟练架设人员可快速完成就位。在两岸锚座先期完工主缆成型的状态下, 若采取两岸同步向跨中架设的方案, 每一片横梁安装就位平均5min, 70m 跨度全桥架设完毕需要3个小时, 而相同跨度的传统贝雷桁架桥至少需要24个小时, 时间缩短很多。

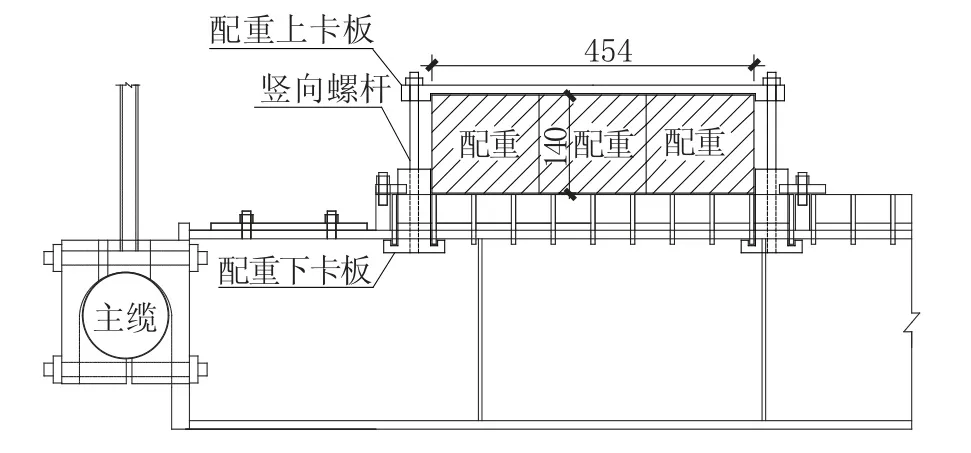
图5 桥面配重横向布置(单位: mm)Fig.5 Lateral layout of bridge deck counterweight(unit: mm)

2 结构体系受力分析

基于Midas Civil 软件, 建立全桥和局部模型, 进行有限元数值分析计算。

2.1 整桥受力分析

全桥计算模型见图6。主缆采用索单元, 横梁、桥面承载板采用梁单元, 桥塔采用梁单元。模型的物理力学参数见表1。边界条件为: 桥塔根部固结约束, 索端为铰接约束。桥塔为纵桥型薄壁构件, 纵向刚度较小, 其顶部节点和对应的索节点简化为共节点铰接。

图6 全桥计算模型Fig.6 Full bridge computing mode

表1 全桥模型物理力学指标Tab.1 Physical and mechanical index of full bridge computing mode

1.主缆找形与初始内力

经非线性计算分析, 主缆在自重和二期恒载、桥面配重作用下(每侧施加)的初始内力等值线图如图7 所示。主缆最大初始内力在缆索根部从根部至跨中2553.2kN ～2489.4kN 递减。

2.倒拆分析

拆除桥梁配重载荷后主缆线形及变位如图8所示, 拆除横梁和桥面承载板后的主缆线形及变位如图9 所示。从图9 可以看出, 拆横梁和桥面承载板后, 主缆跨中垂度向上变位1.3092m, 此时对应的缆索垂度为0.4306m, 主缆最大对应的内力为714.5kN ～756.3kN。

图7 主缆初始内力等值线图(单位: kN)Fig.7 Isogram of initial internal force of main cable(unit: kN)

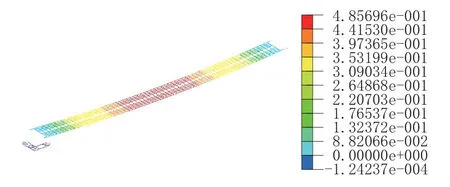
图8 拆除桥梁配重载荷后主缆线形及变位等值线图(单位: m)Fig.8 Contour map of main cable shape and displacement after removing bridge counterweight load(unit: m)

图9 拆除横梁和桥面承载板后的主缆线形及变位等值线图(单位: m)Fig.9 Contour map of main cable shape and displacement after removing cross beam and bridge deck bearing plate(unit: m)

3.主缆在活载作用下的受力分析

通行特载的轮载及轴载布置见图10。特载车辆前后轴距12m, 单轴重13t, 共6 轴, 总重78t, 相较于一般公路标准车, 该特载要超重很多。横向轮距2.5m。荷载横向布置分为对称和非对称两种情况加以分析。

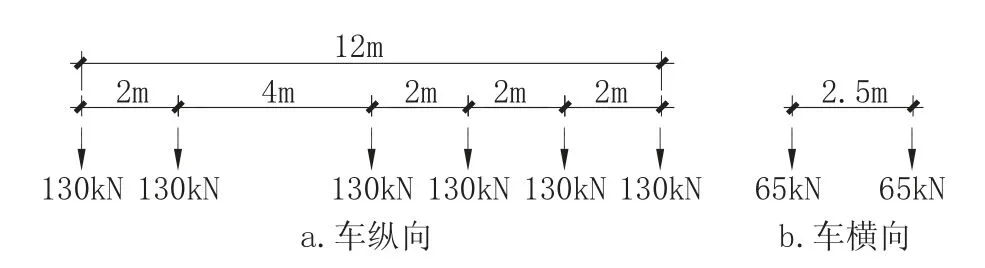
图10 特载车辆布置Fig.10 Special vehicle layout

(1)对称布设的活载。活载作用位置考虑3种: 主跨端部、1/4 跨、跨中, 对应的主缆纵坡分别为13%、10%、7.3%, 对应的主缆最大索力分别为3401.4kN、4170.3kN、4408.8kN, 远低于主缆断裂强度。活载作用跨中结构变位对应的主缆索力等值线云图见图11。

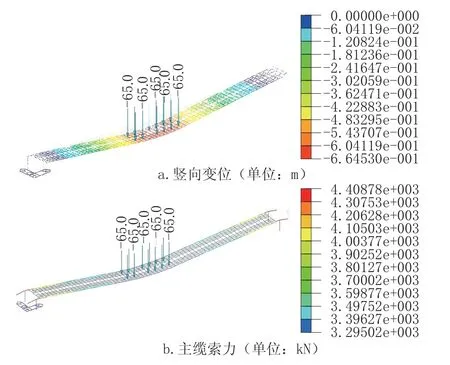
图11 活载作用位置位于跨中时主缆竖向变位及索力等值线云图Fig.11 Contour map of main cable force and vertical displacement when live load is located at midspan

(2)偏载0.3m 布设的活载, 如图12 所示。活载作用位置与对称布设相同。在偏载作用下, 偏心侧主缆垂向位移和索力均相应增大, 和对称布设对比, 按照活载作用位置: 主跨端部、1/4 跨、跨中的顺序, 主缆竖向位移依次增加4.5%、6.5%、7.7%, 主缆索力依次增加4.1%、4.7%、4.1%, 横 向 侧 倾 角 度 分 别 为0.81°、1.26°、1.41°, 满足小于3°的横向安全阈值。偏载荷载作用跨中的荷载效应见图13。

图12 活载偏心0.3m 布设图Fig.12 Layout of live load eccentricity 0.3m

图13 偏载活载作用位置位于跨中时主缆竖向变位及索力等值线云图Fig.13 Contour map of main cable force and vertical displacement when eccentric live load is located at midspan

2.2 横梁结构分析

横梁计算模型采用板单元, 模型如图14 所示。边界条件为模拟横梁端部的倒U 型固定装置, 在前后端部截面外100mm 处建立边界节点,端部截面所有节点和对应的边界节点建立刚臂连接, 然后对两个边界节点施加简支约束。应力极值出现在活载局部承压面, 跨中截面最大应力为160.4MPa, 竖向剪应力最大值为115.1MPa, 端部截面最大应力为44.2MPa, 应力值控制在合金钢允许值内, 见图15。以恒载为不变量, 活载为可变量, 进行稳定系数计算。取前4 阶失稳模态, 计算对应的稳定系数为8.2、10.7、11.2、12.1, 大于欧拉稳定系数6 的要求。一阶失稳模态为侧向失稳, 二、三、四阶失稳模态均为轮载直接位置处的横梁腹板压溃失稳。

图14 横梁计算模型Fig.14 Calculation model of crossbeam

2.3 桥面承载板结构分析

桥面承载板计算模型见图16。计算模型为一品桥面承载板, 长3990mm, 宽566mm。约束条件为间距1m(对应横梁位置)竖向约束, 单边侧水平约束。荷载为自重恒载和作用在其上的轮压活载, 轮载和桥面承载板的接触面积按照500mm(横向) ×200mm(纵向)考虑, 将轮压按照接触面积内分布的板单元的节点数转化为节点载荷计入。同时考虑轮载作用在边跨支点、边跨1/4 跨径、边跨跨中、跨中支点、中跨跨中五种工况进行计算分析。轮载位于中跨跨中时的桥面承载板等效应力等值线云图见图17。最大等效应力为118.2MPa, 应力值控制在钢材允许值内, 最大竖向位移0.32mm。以恒载为不变量, 活载为可变量, 进行稳定系数计算。按照轮载布置位置的五种工况, 分别计算失稳模态和对应的稳定系数,最小稳定系数为30.2, 远大于欧拉稳定系数6 的要求。

图15 活载作用下横梁变位等值线云图(单位: m)Fig.15 Contour nephogram of transverse beam displacement under live load(unit: m)

图16 桥面承载板计算模型Fig.16 Calculation model of bridge deck bearing plate

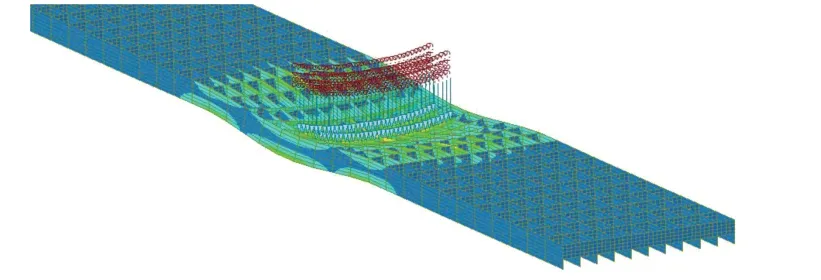
图17 轮载载位下桥面承载板等效应力等值线云图Fig.17 Equivalent stress contour nephogram of bridge deck bearing plate under wheel loads

3 结语

本文介绍了一种适用于应急临时用途轻型、快速架设的缆索支撑的桥梁结构型式, 不但具有承受重载(荷载高达78t)的能力, 而且在两岸锚座先期完工主缆成型的状态下, 具有快速架设的能力。该结构型式具有一系列创新性: 双主缆承载、高强合金铝薄壁箱梁、倒U 型固定装置、密肋桥面承载板、桥面模块化配重等, 经数值计算分析, 满足规范要求。

需要指出的是, 该桥的快速架设是建立在缆索支撑体系已经先期建立的基础上, 且由于桥体自身重量较轻的原因, 其线形并不理想,作为常规通行桥梁是不能满足舒适性要求的,仅作为特殊用途的桥梁型式而存有实用价值。同时其动力特性和抗风稳定性尚需下一阶段深入研究。