基于介电弹性体的漂浮式振荡水柱发电分析*

杜小振， 孔庆帅， 郭 悦， 康 辉

(山东科技大学机械电子工程学院,山东 青岛 266590)

海洋监测为海洋经济发展提供重要保障，当前监测的无线传感装置供电方式主要有化学能电池、太阳能电池等[1]。浮标式波浪能发电结构简单、可实现小型化发电，提供长效电能[2]。宋保维等设计了一种漂浮式永磁发电机并计算分析波浪高度和周期与发电量之间的关系[3]。Falcão等对漂浮式涡轮发电机完成了数值计算和仿真分析，结果显示涡轮直径越大平均输出功率越大[4]。Chiba S等完成了漂浮式介电弹性体波浪能发电实验分析了偏置电压对输出电能影响。该研究组后续完成系泊介电弹性体薄膜浮子吸收波浪能实验研究，拉伸薄膜分析不同波高引起介电弹性体的形变量，在薄膜半径为4 cm、厚度0.065 mm、波高6 cm和周期1.2 s时输出电量达42 mJ[5-6]。Balazs Czech 等建立介电弹性体发电量计算动态模型并比较恒电荷、恒电压、恒电场3种发电方式输出能量，确定恒电场输出较高[7]。Vertechy R等采用数值计算模型，分析薄膜厚度与面积比、质量比对振荡水柱驱动介电弹性体发电特性影响[8]。本文设计浮子与振荡水柱结合捕获波浪能，振荡浮筒内产生的振荡水柱在气室内形成的活塞运动压缩气体驱动薄膜形变发电，分析过程将AQWA计算浮子所受波浪力等与介电弹性体发电能量计算过程相结合，借助Matlab的Simulink数值仿真功能计算薄膜单次形变转换的电能。

1 漂浮式振荡水柱驱动介电弹性体发电工作原理和理论仿真分析方法

漂浮式振荡水柱发电机是由介电弹性体发电系统与浮体组成见图1(b)。浮体为轴对称结构的大直径空心圆柱体，其空心部分构成振荡气室，对海平面上任意方向入射波具有同等效率动能捕获能力。浮标与气室内水柱随波浪起伏上下直线运动的同时因浮标惯性作用使二者形成位移差，振荡水柱压缩气室内空气驱动介电弹性体形变，引起薄膜表面积、厚度(即上下电极间距)发生改变(见图1(a))。介电弹性体薄膜上下表面分布电极等效为可变电容，当施加偏置电压后随着薄膜形变输出电能，实现波浪能到电能转换。

振荡水柱驱动介电弹性体发电理论与仿真联合分析方法步骤见图2，首先建立浮子在波浪作用下的ANSYS水动力分析模型，即：AQWA模型，设置波浪周期、海水密度、浮子重心等初始参数，经水动力学分析输出浮子所受波浪力、辐射阻尼、附加质量；浮子水动力学分析结果作为振荡浮子运动分析初始参量与浮子运动方程结合采用Simulink数值仿真求解介电弹性体薄膜顶端位移，与薄膜形变发电机电耦合换能方程结合计算系统输出能量。

图1 漂浮式振荡水柱驱动介电弹性体发电工作原理Fig.1 The principle of floating oscillating watercolumn power generation with dielectric elastomer

2 漂浮式振荡水柱动力学分析

2.1 振荡浮子运动分析

浮子随波浪起伏做上下变速运动过程受到自身重力、波浪力、流体阻力等因素影响，浮子运动过程带动其周围流体产生变加速运动，依据牛顿第二定律，浮子所受合力为浮子质量和流体附加质量与其加速度的乘积，同时浮子运动对波浪反作用产生辐射阻尼力。基于以上分析则浮子运动方程为[9]：

(1)

式中：M为浮子质量与附加质量之和；Fw(t)为水动力；FR(t)为阻尼力；Fg(t)为物体所受重力与浮力之差。

建立如图1(b)坐标系，零点为波浪平均液面，水面以上为正，以下为负。(1)式中浮子在频率为ω的余弦波浪驱动下形成的运动学方程为：

(2)

式中：m为浮子质量；ma为浮子附加质量；R为辐射阻尼；Po(t)为气室压强；F为浮标垂荡所受波浪力幅值;zs(t)为浮子垂直位移；A1为气室横截面积；A2为浮子横截面积，H为波高；ω为波浪频率；t为时间变量；α为波浪相位；ρw为水密度；g为重力加速度。

设计圆柱形浮体结构外径0.5 m、高0.6 m、气室半径0.1 m、气室高度0.3 m，利用多体流体动力学软件AQWA对浮子垂荡进行频域分析，本文结合青岛近海岸波浪年平均周期为3.4～4.6 s，远海岸波浪周期较近海岸大，则设置波浪周期为5 s。波浪力与波高线性相关，系统输入波高设定为1 m，设置边界条件无限水深，吃水深0.7 m，根据浮子结构尺寸和波浪参数线性分析浮标运动方程(2)式中的相关参量为：浮子受波浪力幅值为6 785.5 N/m、辐射阻尼为47.1 kg/s，附加质量为282 kg。

浮子运动方程采用Simulink仿真模型求解确定浮子位移，如图3，波浪周期与ANSYS AQWA浮子垂荡分析波浪周期设置相同，采用规则正弦波，浮子质量238 kg，海水密度1 025 kg/m3，气室面积0.031 4 m2，浮子横截面积为0.754 m2。

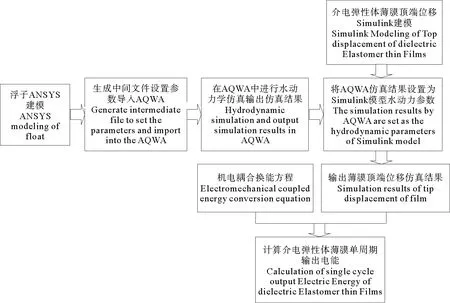
图2 波浪驱动介电弹性体薄膜发电分析流程Fig.2 Analysis flow chart of dielectric elastomers generation driven by wave

图3 浮子运动Simulink求解模型Fig.3 Simulink solution model of float motion

2.2 振荡水柱运动分析

假设波浪为小振幅线性正弦波，即波高远小于波长(H≪L)，无旋运动，则无限水深时，流体坐标z处速度势为：

(3)

式中：k为波数；e为自然常数。

据流体力学原理，速度势对时间求偏导，水深z处的相对压强为：

(4)

将振荡水柱等效为刚性活塞，水柱运动方程：

(5)

式中：B为振荡水柱线性阻尼系数；hw为水柱高度；Patm为大气压强。

根据式(5)建立振荡水柱位移Simulink模型(见图4)，设置参数：吃水深度为0.7 m，波数为0.025 6。

2.3 气室压强计算

气室内空气体积随浮子位移zs与水柱位移zw之间的相对位移变化，气室内压强随之变化，其随时间变化关系为：

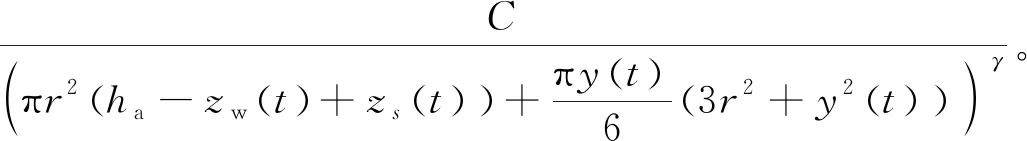
(6)

式中：r为气室半径；ha为气室高度；C为常数；γ=1.4；y为介电弹性体薄膜顶端位移。

浮标与气室内水柱的相对运动形成位移差，水柱压缩气室气体产生压强，其求解过程是利用公式(6)将图2、3两部分仿真结果联合建立Simulink仿真模型见图5，设置参数：气室初始高度为0.3 m，常数C=147 Pa·m3。

图4 振荡水柱位移Simulink求解模型Fig.4 Simulink solution model of oscillating water column displacement

图5 气室压强Simulink求解模型Fig.5 Simulink solution model of pressure in air chamber

3 介电弹性体薄膜形变分析

气室内气体压强驱动介电弹性体薄膜膨胀、收缩，其表面积与厚度随之发生变化，波浪能转化为弹性体薄膜的弹性势能。介电弹性体薄膜受力分析见图6。

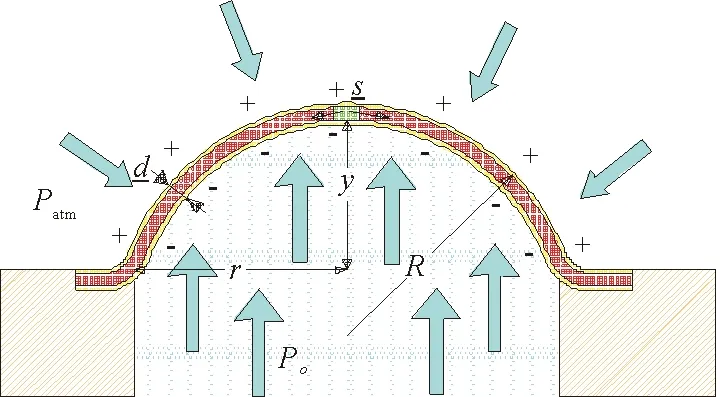
图6 介电弹性体薄膜力学分析示意图Fig.6 Mechanical analysis diagram of dielectric elastomer film

假设介电弹性体薄膜为等双轴拉伸(λ=λ1=λ2)且变形后为球冠面[10]，球冠半径为：

(7)

弹性体薄膜拉伸比：

(8)

式中：r0为薄膜预拉伸前半径；r为预拉伸后半径。

顶端单元位移反映介电弹性体薄膜形变量，在气室压强作用下顶端单元达最大位移量时，受自身应力、重力、气室压强等作用，受力平衡公式为：

(9)

式中：δ0为薄膜为拉伸前厚度；P为弹性体薄膜内外压强差；S0顶端单元面积。

介电弹性体薄膜自身应力包括形变产生的弹性应力和预置电压产生的静电应力，薄膜总应力σ为弹性应力与静电应力之差：

(10)

式中：ε为介电弹性体薄膜的介电常数；μ、I为弹性体本构参数；V为偏置电压。

球冠顶端单元运动方程为：

(11)

式中ρde为弹性体薄膜密度。

将浮子位移与振荡水柱位移联合计算的气室压强Simulink仿真结果作为方程(11)输入，计算介电弹性体顶端位移(见图7)，设置初始参数：介电弹性体薄膜厚度0.25 mm，介电常数4.5×8.85× 10-12F/m，介电弹性体预拉伸后半径10 cm。

图7 介电弹性体薄膜顶端形变位移Simulink求解模型Fig.7 Simulink solution model of the displacement on the top of dielectric elastomer film

研究波浪进入气室驱动介电弹性体薄膜顶端位移量，选取薄膜初始半径5 cm，预拉伸比λ0=2，薄膜厚度0.25 mm。青岛董家口附近全年平均波高为0.5 m，结合浮子计算模型尺寸设计，选取波浪高度分别为0.3、0.4、0.5 m时，介电弹性体薄膜随波浪周期变化的拉伸情况如图8。在波浪周期为T=0.9 s左右时，薄膜位移急剧增大，浮标与水柱之间的相对位移达到最大，处于共振状态，气室内压强产生最大变化。在T=1.5 s时，出现二次谐振现象，但幅值相对较小。为了提高波能转换效率，在弹性体薄膜有效拉伸范围内应利用共振现象，本文根据青岛海域波浪情况分析浪高对波浪形变影响，结果表明薄膜顶端位移随波浪高度增大而增大。

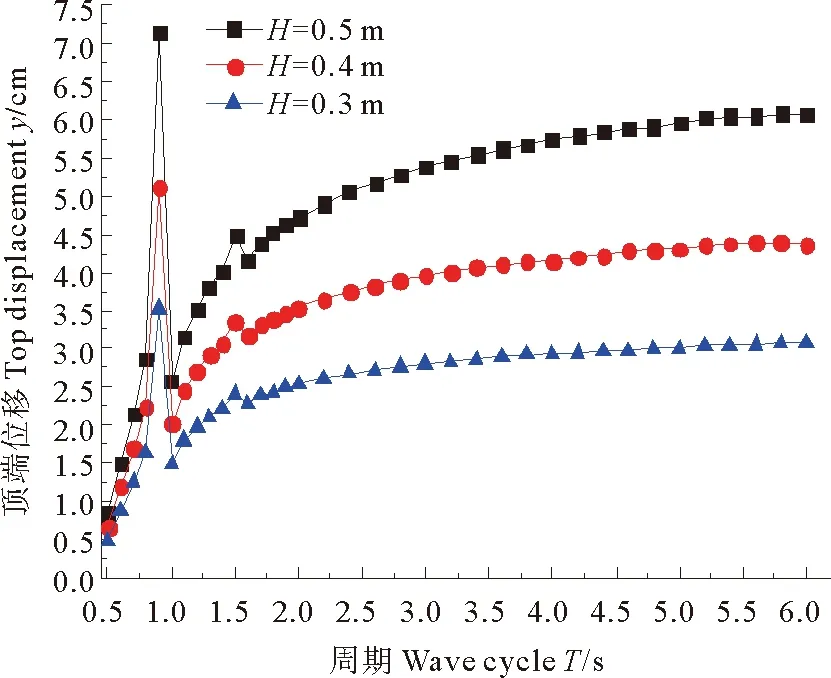
图8 薄膜顶端位移随波浪周期变化Fig.8 Film tip displacement varies with wave period

介电弹性体发电薄膜顶端位移与其初始结构的半径和膜厚几何参数关系见图9。顶端位移随薄膜厚度的增加逐渐减小，薄膜预拉伸前半径越大薄膜顶端位移越大，最大位移为6.4 cm。

图9 薄膜顶端位移随薄膜厚度变化Fig.9 Film tip displacement varies with thickness

4 波浪驱动介电性体发电分析

介电弹性体形变发电原理等效为可变电容发电模型，当机电能量转换薄膜在气室压强外力作用下发生形变：拉伸过程薄膜上下电极表面增加，间距变小，则等效电容变大；施加偏置电压，当弹性体薄膜收缩后，电容减小，输出更高电压，实现机械能向电能转化。如图1(a)，弹性体薄膜预拉伸时电容C0为式(12a)和施加机械力作用动态拉伸后电容Cd为式(12b)。

C0=εr·ε0·π·r2/δ2。

(12a)

Cd=εr·ε0·π·(y2+r2)/δ1。

(12b)

式中：εr为相对介电常数；ε0为真空介电常数，δ1、δ2为薄膜受气压作用前后膜厚。

振荡浮子驱动介电弹性体发电表现为薄膜在气室压强作用下发生拉伸膨胀，对薄膜施加偏置电压Vin，则介电弹性体薄膜所携带的电荷量为：

Qin=VinCd。

(13)

介电弹性体薄膜携带电能为：

(14)

介电弹性体收缩，根据电荷不变原则，此时介电弹性体两端电压为：

Vout=Qin/C0=VinCd/C0。

(15)

收缩后携带的电能为：

(16)

每个拉伸膨胀周期介电弹性体薄膜输出电能：

(17)

介电弹性体材料选用丙烯酸酯(VHB-4910)，丙烯酸酯具有较强的电击穿强度Emax=100 mV/m，可承受最大形变λmax=600%，相对介电常数εr=4.5，真空介电常数ε0=8.85×10-12。

介电弹性体发电薄膜预拉伸前半径为4 cm，厚度为0.25 mm，发电量与顶端位移的变化关系如图10。介电弹性体发电量随顶端位移的增大发电效果好。在击穿电场范围内，偏执电压越大发电量越多，当顶端位移为6 cm时，可输出20.4 mJ能量。当薄膜厚度为0.25 mm，波幅为0.25 m时，预拉伸前半径与发电量变化关系见图11，介电弹性体薄膜随预拉伸前半径的增大减少。当薄膜预拉伸前半径为4 cm，波幅为0.25 m时，薄膜厚度与发电量变化关系见图12，介电弹性体薄膜随厚度增大而减少。

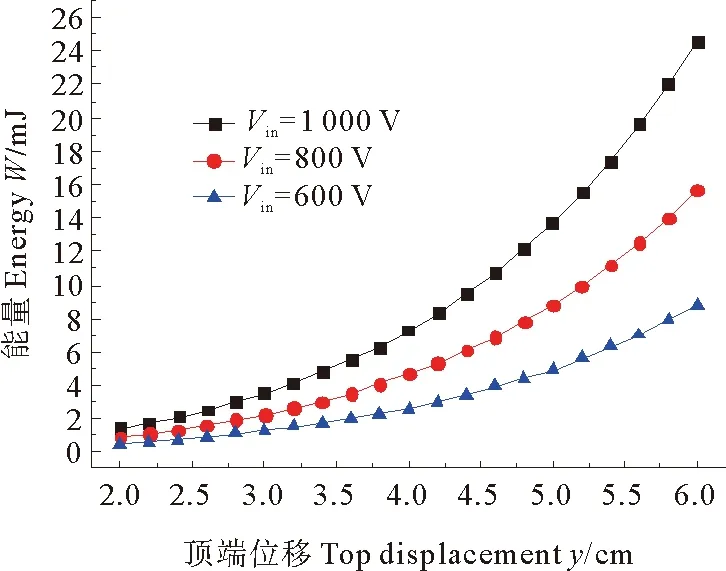
图10 单循环周期发电量与位移关系

图11 单循环周期发电量与拉伸前薄膜半径关系

5 结语

本文研究了浮标式振荡水柱介电弹性体发电理论计算模型，采用ANSYS软件中的AQWA模块分析了浮标所受波浪力、辐射阻尼、附加质量。将理论计算模型与Simulink仿真相结合计算介电弹性体薄膜顶端位移，基于可变电容发电原理计算单次拉伸膨胀周期内产生发电量最高为24.6 mJ。波浪驱动介电弹性体发电理论为提高能量转化效率，建立海上浮标长效自供能技术提供理论基础。

图12 单循环发电量与预拉伸薄膜厚度关系