基于实时含水率数据的土壤墒情动态建模及预测*

王铁英，王仰仁**，战国隆，牛少卿，姚 丽

基于实时含水率数据的土壤墒情动态建模及预测*

王铁英1，王仰仁1**，战国隆2，牛少卿2，姚 丽1

（1. 天津农学院水利工程学院，天津 300392；2. 天津市大禹节水灌溉技术研究院，天津 301712）

实时准确地预测墒情是进行灌溉预报，实现农田水分精准化管理，提高水分利用效率的重要措施。基于根区（0−60cm土层）水量平衡原理，利用泰勒级数对根区下界面水分通量和作物蒸腾量进行了线性化处理，并以实时根区平均土壤含水率为自变量构建了动态的土壤墒情预测模型。采用天津市武清区西吕村无线土壤墒情监测系统（包含3个监测点）实时监测数据（地表下30cm和60cm处的土壤含水率），分别选取5d、10d、15d和20d作为建模系列长度进行回归分析，确定模型参数，对10d和15d两种预见期进行了土壤墒情预测精度分析。结果表明：（1）实时预测模型拟合程度较好，三种建模系列长度条件下的确定性系数均达到0.80以上（样本数均大于550）；（2）15d建模系列长度下相对误差最小；（3）15d建模系列长度、15d预见期、10%相对误差界限值条件下，3个监测点的墒情预测合格率分别达到98%、100%和89%。由此可见，研究提出的实时墒情预测模型预测精度较高，便于建模分析，为土壤墒情的预测提供了新方法。

土壤墒情；动态建模；传感器；水量平衡；墒情预测

土壤墒情是指土壤中的水分状况，它的时空分布对气候因子变化非常敏感，是影响农业生产的重要因素。因此，在一定的时间和空间尺度上掌握土壤水分的动态变化规律，对于提高作物产量、有效利用水资源具有重要作用[1−4]。土壤墒情预测，即确定未来某一时期土壤含水率的多少，对于准确进行灌溉预报具有重要意义[5]。土壤墒情的预测方法较多，研究时间较长，到目前为止，采用的模型及方法主要分为水量平衡模型[6]、土壤水动力学模型[7−8]、消退指数法[9]、BP神经网络法[10−11]、时间序列分析法[12−13]、遥感监测法[1,14]、经验统计法[15−16]等。水量平衡模型是通过研究水量平衡方程中有效降水量、农田蒸发蒸腾量、地下水补给量等参数之间的相互影响关系，确定土壤水分收支变化来进行墒情预测，其原理简单，但是建立模型所需参数较多；土壤水动力学模型是根据土壤水分运动基本方程，在研究地表蒸发、作物蒸腾、根系吸水等随作物生长变化规律基础上，进行土壤含水率预测，具有坚实的物理基础，但同样存在较多难以测定的土壤和作物参数；消退指数法是通过分析消退指数与其影响因素之间的相关关系，建立消退指数与其影响因素的经验统计模型，据此进行墒情预测，所需参数较少且易获得，但是受根区下边界水分环境影响较大；BP神经网络法是利用网络结构和参数来反应土壤水分变化与主要影响因素之间的关系，所使用的土壤、作物等参数没有具体物理意义；时间序列法是通过研究土壤含水率的趋势性变化、周期性变化和随机变化规律，进而建模并做出预测，但是受年际间气候因素变化影响较大；遥感监测法主要是通过建立影响土壤含水率的热惯量、归一化植被指数等因素与土壤含水率之间的统计模型来进行墒情预测，可通过卫星遥感资料及时了解区域水分变化，但所建立的预测模型的准确性和稳定性有待进一步研究；经验统计法是用影响土壤水分的因素建立起来的经验模型，方法应用简单，但是预报模型的经验系数因土壤和作物的不同会有较大变化，且建立的模型只适用于特定地区[5,17−18]。

上述模型及方法具有一个普遍的特点，利用某一时期墒情数据确定模型参数，然后对未来一段时间的土壤含水率进行预测。如唐春燕等[17]利用江西省南康市、湖口县两地1999−2008年的土壤墒情资料及同期气象资料采用逐步回归分析方法分5个或4个时期建立了土壤墒情预测的经验统计模型，利用两地2009−2010年的资料进行了模型检验，南康的预测精度达到了70%～100%，湖口的预测精度达到了60%～77%；孙秀邦等[2]利用安徽省砀山、亳州、蒙城、宿州及阜阳5个站点1981−2003年的土壤墒情数据及气象数据，分春、夏、秋、冬四季回归分析建立了可应用于淮北地区的数理统计预测模型，并采用淮北地区其它16个县市2005年农业气象观测站资料进行验证，平均预测精度达到91.3%；马晓刚[19]选择辽宁阜新地区阜蒙县气象站1981−2003年春播关键期4月10−50cm土层的平均土壤墒情及该站1980−2002年秋季(9−11月)降水量，以对数函数形式建立了春播关键期土壤墒情与上年秋季降水的统计关系，利用2004−2006年的降水及墒情数据进行预测检验，其预测相对误差平均为6.82%。该类方法包含了一个假定，除模型考虑的环境因素外，忽略了其它环境因素在预测期和建模期的变化，一定程度上降低了预测精度。传感器[20−22]与互联网技术的普遍应用促进了土壤墒情的实时获取。本研究利用实时监测墒情数据，基于农田水量平衡的原理建立动态的土壤墒情实时预测模型，以一定时间长度的建模系列动态化地确定模型参数，并进行墒情预测。该方法区别于现有方法的实质是，能够利用动态化的模型参数实时捕捉最近一段时间影响土壤墒情环境因素的变化，可显著提高墒情预测精度。

1 材料与方法

1.1 实时墒情采集与数据处理

墒情数据取自无线土壤墒情监测系统2017年11月7日−2019年9月20日共计625d的实时土壤含水率数据。土壤墒情监测系统的基站位于天津市武清区崔黄口镇西吕村示范区，示范区面积为140hm2，主要种植大田作物为冬小麦和玉米。基站控制3个节点，节点分布情况见图1，每个节点连接两个土壤水分传感器，分别位于地表下30cm和60cm处，以1h为时间间隔对土壤墒情信息进行采集。为研究方便采用每日24h数据的平均值作为日数据。节点采集的墒情数据以无线方式发送到基站，通过互联网短信方式传输至信息管理中心。通常情况下，墒情预测和灌溉预报均以0−60cm土层含水率平均值为依据，对此，李泳霖等[23]针对本示范区给出的方法及结果，将以日采集的30cm（x1）和60cm（x2）处实时含水率数据转化为0−60cm土层平均含水率（θ），并作为0−60cm土层含水率实测值，即

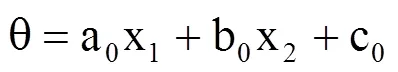
式中，θ为0−60cm土层的平均含水率（cm3·cm−3）；x1和x2分别为地表下30cm和60cm土层含水率的实测值（cm3·cm−3）；a0、b0和c0为待定参数，其结果分别为0.645、0.264、1.868[23]。

1.2 模型构建及参数确定

1.2.1 模型构建

在农田水分变化过程中，降水、灌水、作物蒸腾和下边界水分运移（包括地下水的补给量及土层内的水分下渗量）是农田水分变化的主要影响因素，因此可以列出在某一时段内、一定深度土层的水量平衡方程[6,24−25]，即

式中，Wi+1为时段末土壤储水量(mm)；Wi为时段初土壤储水量(mm)；Pi为时段内的降水量(mm)；Mi为时段内的灌水量(mm)；Ki为时段内土层的下边界水分运移量(mm)；ETi为时段内农田的蒸散量(mm)；i为时段编号，i=1，2，3，…，n；n为时段数，称为建模系列长度，取n等于5、10、15和20d。

无线土壤墒情监测系统中给出的土壤含水率数据为体积含水率，因此，水量平衡方程即式(2)可转化为

式中，H为土层厚度（mm）；θi+1为时段末土壤含水率（cm3·cm−3）；θi为时段初土壤含水率（cm3·cm−3）。

式(2)、式(3)中下边界水分运移（Ki）[26−27]，其大小与地下水埋藏深度、土壤性质、作物种类、作物耗水强度、气象条件和根系层土壤含水量等有关，可将其表达式写为Ki=k（根系层土壤含水量，地下水埋藏深度，气象条件等）。作物的蒸散量（ETi）[28]大小与气象条件（温度、日照、湿度和风速）、土壤含水状况、作物种类及其生长发育阶段、农业技术措施、灌溉排水数量等有关[29-30]，可将其表达为ETi=f（土壤含水状况，气象条件，灌溉排水数量等）。影响Ki和ETi的各个因素互相关联，其中部分因素较难实时获取准确的数据，因此，在一定时段（以日为单位）内以土壤含水率为主要变量，将其它因素作为常量，对Ki和ETi分别进行泰勒级数展开，保留展开式的常数项及一次项可得到

式中，k0、e0为级数展开后的常数项；k1、e1为级数展开后一次项参数。

将式（4）、式（5）带入式（3），得到

令，a=( k0−e0)/ H，b=（1+ k1−e1）/H，由此得到实时墒情预测模型（简称为实时模型）即

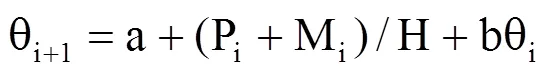
式中，a、b为待定参数。由上述建模过程可以看出，模型参数a、b包含了作物生长动态、天气因素变化和地下水埋深情况等环境因素对墒情变化的影响。

1.2.2 参数确定

假定获得了一组土壤含水率监测序列θt(t=1，2，3，…，T)，t为土壤含水率编号，T为土壤含水率监测序列长度。以n为建模系列长度，从t=1开始取n+1个值，将1d作为一个时段，共有n个时段，以时段初的值作为自变量，将时段末的土壤含水率值作为因变量，通过回归分析，可得到一组参数a1、b1，从t=2开始进行相同处理，可得到a2、b2，依次类推，可得到该组墒情监测序列随时间变化的全部参数值，共有T−n+1组。

回归分析过程中，若时段末含水率大于时段初的含水率，认为是灌水或降水引起的，其降水或灌溉数量(Pi+Mi)用式（8）求得，即

若时段末含水率小于时段初含水率，则认为

式（8）、式（9）是对实时监测土壤含水率数据的一种处理方法，该方法避免了降水和灌溉数据的直接获取。

由于时段内蒸发蒸腾对水分的消耗，因而只有当时段内的降水或灌水量足够大的时候才会出现θi+1大于θi的情况，较大的降水或灌溉量会引起土壤含水率的突然增大，从而导致土壤墒情预测误差的显著增大，故引入参数Δθ，当θi+1+Δθ−θi>0时，采用式（8）计算降水或灌水数量，否则认为降水和灌水为零。

1.2.3 墒情预测

当得到一组参数a和b后，即可按式（10）进行土壤含水率的预测，即

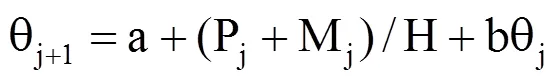
式中，j为时段编号，j=n+1，n+2，…，n+k，k为预见期长度；对于降水量Pj可以采用天气预报数值；墒情预测的目的是进行灌溉预报，因此在墒情预测过程中，Mj可取为0。

为保证预测结果的准确性，参照已有研究[12,17]，对未来15d（预见期为15d）进行预测精度分析，同时补充10d预见期的精度分析。预测过程中，若预测值大于饱和含水率或小于枯萎系数，认为当日确定的a、b为不合理参数，采用前一日所确定的实时模型参数进行预测，若仍不满足要求，则采用更前一日实时模型参数进行预测。

1.3 实时模型的评价方法

基于实时监测的数据可对一定预见期内0−60cm土层平均含水率进行预测，采用相对误差（δR）、确定性系数（DC）和合格率3种评价方式对模型及预测结果进行评价。其中相对误差值和合格率主要用于评价预测结果的准确性，确定性系数用于实时模型的拟合程度评价。

（1）确定性系数

确定性系数（DC）表示模型的模拟值与实测值的接近程度，本研究采用动态回归，计算结果是对短期内农田含水率变化规律的一种体现，建模系列长度较短，当土壤含水率出现较大变化时，会使回归结果无法较好地体现含水率的变化规律，模型的拟合程度降低，最终导致过大的预测误差，因此，对建模过程中的确定性系数进行计算分析，计算方法见式（11），其大小在一定程度上反映了所建立回归模型的可靠程度，其数值在0～1范围变化，数值越大表明拟合程度越高，模型的可靠性越高。

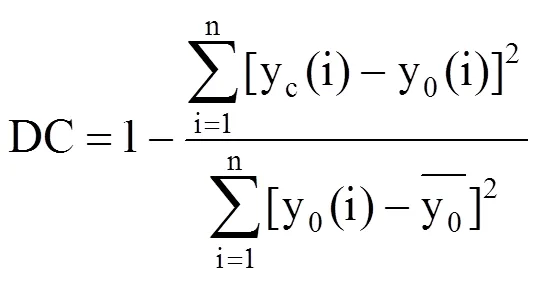
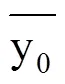
（2）相对误差

例如，教师可以结合着社会生活的热点来创设相应的教学情境。如在湘教版数学七年级上册第3章《一元一次方程》的教学中，教师可以引入一个飞机拦截的情境：中国在2013年划设了东海放空识别区，中国空军和海军经常会出海拦截外国的不明飞机。我们假设小李是一名飞行员，驾机执行拦截任务，他从地面匀速加速起飞，10秒后达到了350km/h的离地速度，随后到60秒时匀速加速到了1500km/h的巡航速度赶赴目标空域。根据这个情境，教师可以组织学生们解相关的一元一次方程。这是一个新颖的话题，而且是两段情境，具有挑战性；初中生又具有朴素的爱国主义情怀，在解题情境中表现积极：

相对误差（δR）表明了土壤墒情预测值与实测值间的差异，其值越小说明预测的精度越高，预测模型的准确性程度越高。计算式为

式中，Mj、Sj分别为0−60cm土层平均含水率的实际值和预测值（cm3·cm−3）。

（3）合格率

合格率（QR）用来检验预测结果的合理性，也是表示模型预测精度的一个指标，其值是指在允许误差范围内的预测次数占总预测次数的百分数，计算方法见式（13）。预报要素和预报方法不同时，允许误差范围有所差异，墒情预测中尚未有允许误差范围标准值，因此参照已有研究[2,9,10,17,12,30,31]，将0−60cm土层平均含水率预测值的相对误差作为计算样本，以5%、10%和15%三种相对误差作为允许误差界限进行合格率的计算。

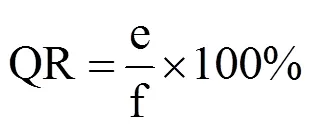
式中，QR为合格率（%）；e为合格预测次数，合格预报次数指在允许相对误差范围内的次数；f为预测的总次数。

2 结果与分析

2.1 参数a、b的结果分析

参数a、b包含了作物生长动态、气象条件和地下水位变化等环境因素对土壤墒情动态变化的影响，这些环境因素随时间和空间位置是动态变化的，因而参数a、b也随时间和空间而变化，模型参数的这一特性显著提高了预测精度。图2中给出了节点一处，10d建模系列长度条件下待定参数随时间的变化过程。由图可以看出，（1）参数a、b均围绕其平均值上下波动。结合表1，在节点一处随建模系列长度增大，参数a的平均值减小，对应5d、10d和15d建模系列长度的平均值分别为0.0412、0.0300和0.0244；参数b的平均值逐渐增加，对应5d、10d和15d建模系列长度的平均值分别为0.8354、0.8801和0.9027。

（2）参数a、b均有少数过大或过小的峰值出现，且参数a、b的峰值同步出现。模拟预测时发现，这些峰值处的参数无法用于预测土壤含水率的变化，为不合理参数，不合理参数的数量随着建模系列长度的增加而减少，对于节点一，5d建模系列长度时，不合理参数的组数达到48组，占总样本数的8.0%；10d建模系列长度时有21组，占总样本数的3.6 %；而15d建模系列长度时仅有9组，占总样本数的1.6 %。对于合理的实时模型参数，可根据参数的最大值和最小值作为变化范围的上限和下限（表1），实时模型参数在此变化范围内波动，结合表2分析发现，变化范围随建模系列长度变化，其中参数a的变化范围下限值随建模系列长度的增加而增大，上限则随建模系列长度的增加而减小；参数b的变化范围的上下限随着建模系列长度的增加具有与参数a相同的变化趋势。

图2 节点一处10d建模系列长度下模型参数随时间的变化过程

（3）参数a、b变化过程线有间断点，主要原因是墒情监测设备出现故障，及时排除故障，并不会长时间内对建模及预测结果产生影响。

对于示范区的节点二和节点三，也进行了相同的处理，并得出相应的参数a、b的均值和变化范围，由表1可见，节点二和节点三处的实时模型参数变化与节点一具有相同的趋势，但是其均值及变化范围有所差异。不同节点所确定的实时模型参数的差异性，一定程度上反应了不同节点处土壤含水率的空间差异性。

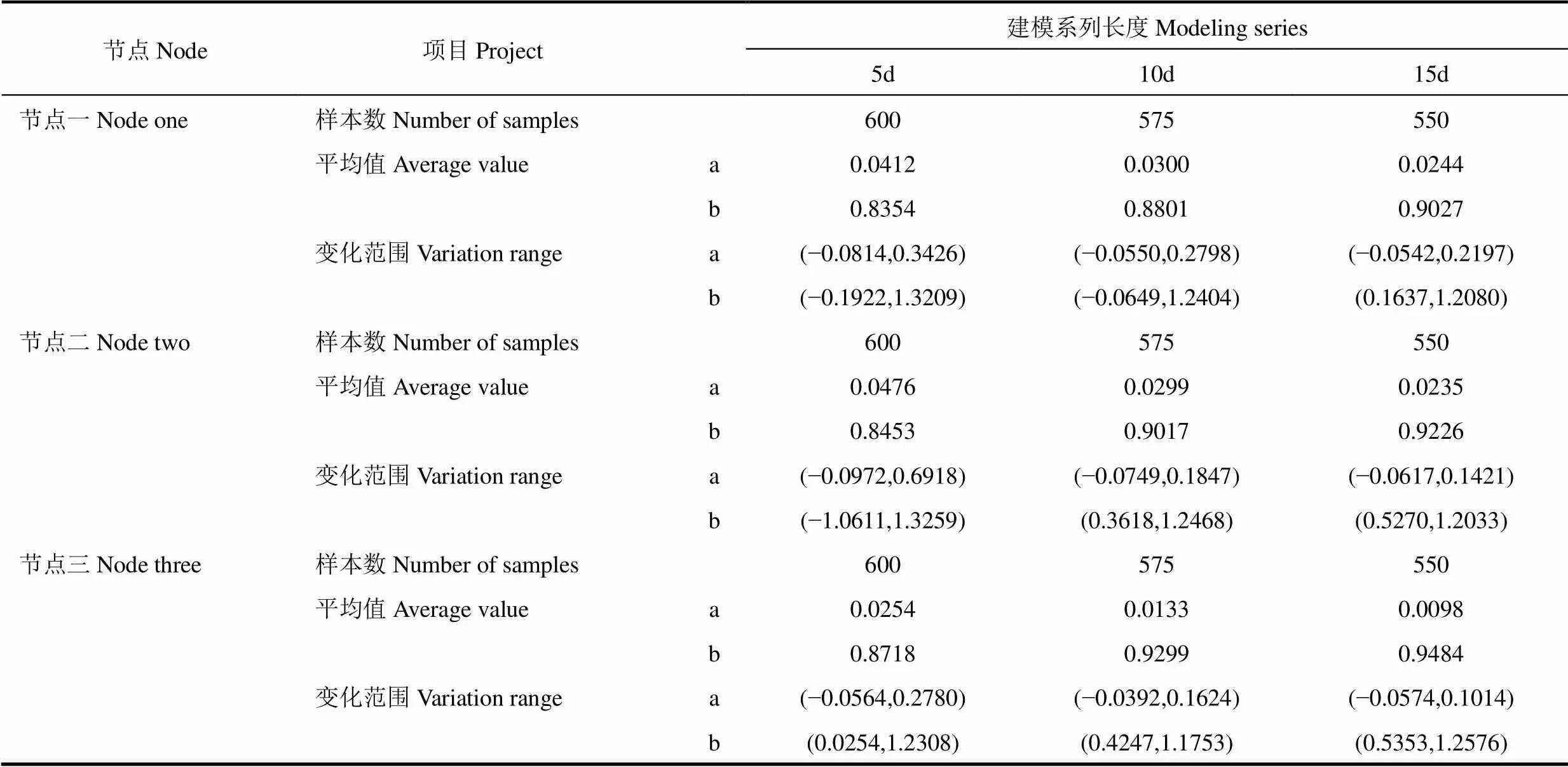
表1 三个节点模型参数随建模系列长度的变化

2.2 实时模型拟合程度及预测误差分析

2.2.1 实时模型拟合程度分析

根据式（11）计算得到确定性系数，对模型拟合程度进行评价。确定模型参数时，在选取的土壤含水率数据中，共包含625d的含水率数据，由于建模系列长度的不同，回归分析样本数有所不同，15d建模时对应的样本数最少，为550，相应地得到550个确定性系数；同理得到不同建模系列长度条件下的确定性系数均值。由表2可知，随着建模系列长度的加大，确定性系数均值逐渐增大，5d建模系列长度下第二节点的确定系数最小，也在0.82以上；各节点确定性系数随建模系列长度表现出了相同的变化规律。

表2 三个节点不同建模系列长度下的确定性系数平均值

注：建模系列长度为5d、10d和15d的样本数分别为600、575和550。

Note: When the modeling series is 5,10 and 15 days, the number of samples is 600, 575 and 550, respectively.

2.2.2 实时模型预测误差分析

实时模型的预测误差是评价和选择模型的重要依据。利用确定的实时模型参数，对未来15d的农田含水率进行预测，根据式（12）计算得到相对误差。对每一个节点分5d、10d、15d、20d四种建模系列长度进行预测误差分析；对于每种建模系列长度，分10d和15d两种预见期给出了每次预测相对误差的最大值、平均值和最小值，再计算整个监测系列长度的相对误差均值，结果见表3。由表可见，无论哪个节点，均以15d建模系列长度的相对误差最小；以平均相对误差而言，10d预见期的相对误差均小于15d的相对误差；在15d建模系列长度下，对应10d和15d预见期的相对误差，三个节点之间有所差异，最大值分别为2.94%和4.52%（节点三），最小值分别为1.13%和1.16%（节点二）。

表3 不同节点、建模系列长度和预见期条件下土壤含水率预测值的相对误差均值（%）

2.3 实时模型预测结果的合格率分析

预测结果的合格率是评价模型预测精度的重要指标。前述分析表明建模系列长度为15d时，模型的预测精度最高。针对该模型，以5%、10%和15%三种相对误差界限值给出了10d、15d两种预见期下的预测合格率，相应10d和15d预见期条件下的样本数分别为508、483。合格率计算结果见表4。由表可以看出，预测合格率随着相对误差界限值的增大而增大，随着预见期的增大而减小。不同节点处预测合格率有一定的差异，其中以节点二的预测合格率最大，对应10d预见期的三种相对误差界限值的合格率分别为99%、100%和100%；对应15d预见期的三种相对误差界限值的合格率分别为97%、100%和100%。以节点三的预测合格率最小，对应10d预见期的三种相对误差界限值的合格率分别为88%、96%和97%；对应15d预见期的三种相对误差界限值的合格率分别为79%、89%和94%。不同节点处合格率的差异在一定程度上反映了实时模型在农田空间尺度上的变异性。

2.4 Δθ取值

Δθ是在确定模型参数过程中，用以判断是否计算某时段内降水和灌水量的数值，当时段末与时段初土壤含水率之差≥该值时，即认为引起含水率增加的原因为降水或灌水，并由此计算降水和灌水值；否则认为降水或灌水数量等于0。在土壤墒情预测过程中，降水和灌水是导致墒情预测出现偏差的主要原因，因此，Δθ的取值大小对确定模型参数过程中的土壤含水率模拟值与实测值的拟合程度和实时模型预测过程中的预测精度会造成很大的影响，基于此，采用节点一处2017年11月7日−2019年9月20日时段内的土壤含水率数据，设定不同大小的Δθ取值，进行建模并做出预测，得到不同情况下的模型拟合程度变化（图3）以及实时模型预测精度变化（图4）。由图3可见，随着Δθ的增大，对应5d、10d和15d三种建模系列长度的确定性系数均呈减小趋势，在Δθ为0时，具有最大的确定性系数值，实时模型的拟合程度最高。由图4可见，除5d建模系列之外，10d和15d建模系列，随着Δθ的增大，10d和15d两种预见期下预测结果的平均相对误差均值明显出现了随Δθ的增大而增大的趋势。5d建模系列长度时，随着Δθ的变化，两种预见期下预测结果的平均相对误差均值变化较小，10d预见期时较为平缓，15d预见期时具有小幅度的增加趋势。

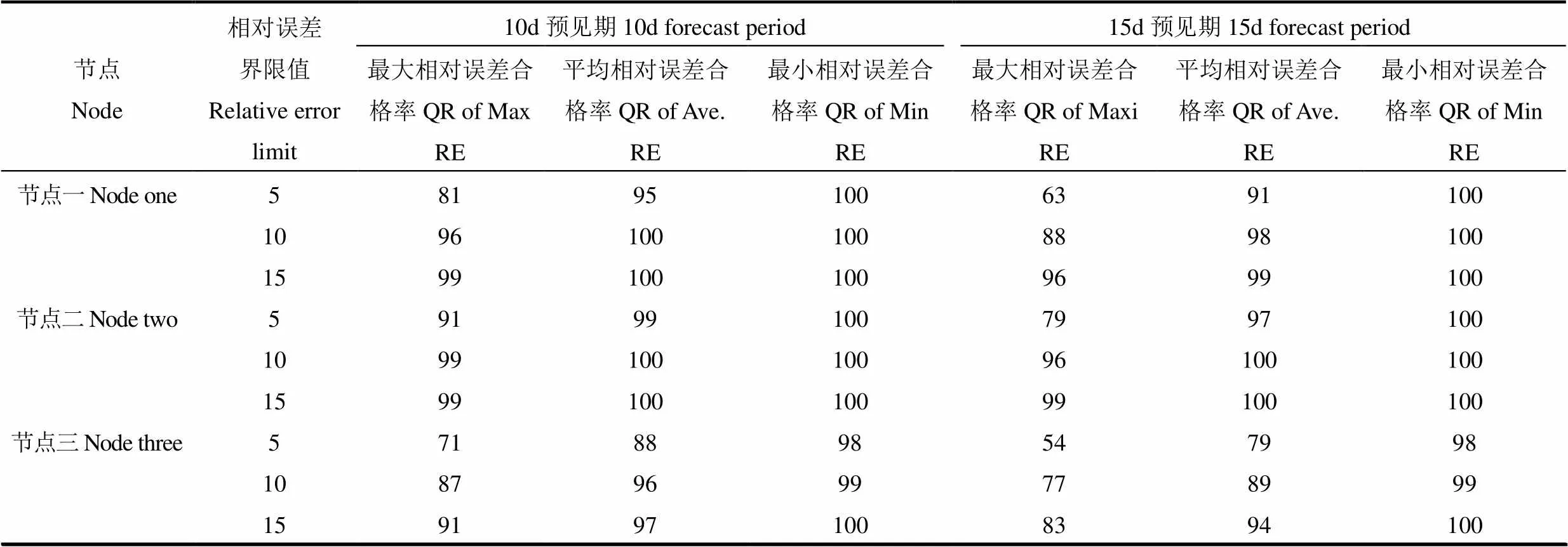
表4 三个节点15d建模系列条件下土壤含水率预测结果的合格率（%）

综合分析对比Δθ不同引起实时模型拟合程度以及预测精度的变化情况，本研究中取Δθ= 0。

图3 不同建模系列下确定性系数随Δθ的变化

图4 实时预测模型的预测相对误差均值随Δθ的变化

3 结论与讨论

3.1 讨论

目前使用的一些墒情预测方法，常采用固定参数进行预测，不能较好地捕捉环境因素的变化，因此建立了动态的墒情预测模型，可实现每日建模预测。模型具有较高的拟合程度及预测精度，15d建模系列长度时，三个监测节点确定性系数达到了0.93以上；10d、15d预见期时预测相对误差分别在1.13%～2.94%和1.66%～4.52%。以合格率对模型预测精度进行检验，10d和15d预见期的合格率分别达到97%和94%以上。

本研究建立的实时模型较其它预测模型在预测精度上有所提高。李宝五[30]采用BP神经网络法、彭曼公式P-M两种方法模拟作物蒸散量，后根据水量平衡原理以旬为时段分别建立了土壤含水率预测模型，基于P-M公式的水量平衡模型对土壤含水率的预测值与实测值的平均相对误差为9.7%，基于BP神经网络法的平均相对误差为6.3%；张雪飞[31]依据SIMPEL模型对德国奥斯纳布吕科技大学4个试验区小麦生长期内的土壤含水量进行了分层（0−10、10−20、20−30和30−40cm）模拟，分析发现研究地区土壤含水量实测值与预测值相对误差在0.8%～13.3%，相对误差平均为5.6%。张雪飞等所做的研究中较系统考虑了作物蒸发蒸腾的变化对墒情预测的影响，但未考虑其它影响土壤墒情的因素，因而其给出的预测误差均大于本研究结果。除此之外，现有研究方法建立的预测模型，其预测精度也低于本研究给出的结果，牛宏飞等[32]对北京延庆2010−2015年的土壤墒情和气象数据进行分析，以线性回归法、BP神经网络法和PCA-KBF神经网络法分别建模，并取用2016年的100组数据进行预测分析，其预测误差值依次为5.4%、4.3%和5.8%，与本研究的预测误差接近，但仍然略为偏大。

分析时通过引入Δθ从实时监测的土壤墒情数据中识别出了降水量和灌溉量，在一定程度上提高了模型的拟合程度和预测精度，但是降水仍然是影响墒情预测的一个输入因素，在预测过程中需要利用天气预报的降水量数据，因此降水量预报精度，是影响墒情预测精度的重要因素。

3.2 结论

（1）传感器与互联网结合构成无线土壤墒情监测系统，可实时、准确监测传输土壤墒情信息并储存，在此基础上依据水量平衡原理构建墒情预测的动态模型，通过回归分析确定的动态模型参数实时反映了影响农田墒情的环境因素的变化，模型具有较高的预测精度。

（2）对5d、10d、15d和20d建模系列长度条件下的预测分析表明，15d建模系列下预测精度最高，对应10d、15d预见期的相对误差为2.94%和4.52%。

（3）基于2017年11月7日−2019年9月20日共计625d的土壤含水率数据，分析研究实时墒情动态模型参数及其预测精度，结果表明，采用该模型进行墒情预测时，并不需要长序列的观测数据确定模型参数。

[1] 李亚春,徐萌,唐勇.我国土壤水分遥感监测中热惯量模式的研究现状与进展[J].中国农业气象,2000,21(2):41-44. Li Y C,Xu M,Tang Y.The status and advances of thermal inertia models in measuring soil moisture by remote sensing in China[J].Chinese Agricultural Meteorology,2000, 21(2): 41-44.(inChinese)

[2] 孙秀邦,严平,黄勇,等.淮北地区土壤墒情动态预测[J].合肥工业大学学报(自然科学版),2007(9):1144-1147. Sun X B,Yan P,Huang Y,et al.Dynamic forecasting of soil humidity in the Huaibei area of Anhui Province[J].Journal of Hefei University of Technology (Natural Science Edition),2007(9):1144-1147.(inChinese)

[3] Wu Z Y,Zhou J H,He H,et al.An advanced error correction methodology for merging in-situ observed and model-based soil moisture[J].Journal of Hydrology,2018,566:150-163.

[4] Kolassa J,Reichle R H,Liu Q,et al.Estimating surface soil moisture from SMAP observations using a Neural Network technique[J].Remote Sensing of Environment, 2018,204: 43-59.

[5] 粟容前,康绍忠,贾云茂.农田土壤墒情预报研究现状及不同预报方法的对比分析[J].干旱地区农业研究,2005,23(6): 194-199. Su R Q,Kang S Z,Jia Y M.Research status of soil moisture forecast in farmland and comparative analysis of different methods[J].Agricultural Research in Arid Regions,2005, 23(6):194-199.(inChinese)

[6] 刘勇洪,叶彩华,王克武,等.RS和GIS技术支持下的北京地区土壤墒情预报技术[J].农业工程学报,2008(9):155-160. Liu Y H,Ye C H,Wang K W,et al.Soil moisture prediction technique in Beijing supported by RS and GIS techniques[J]. TransactionsoftheCSAE,2008(9):155-160.(in Chinese)

[7] 蒋太明,刘海隆,刘洪斌,等.黄壤坡地土壤水分垂直变异特征分析[J].农业工程学报,2005(3):6-11. Jiang T M,Liu H L,Liu H B,et al.Analysis of vertical variation characteristic of soil moisturein yellow soil sloping field[J].Transactions of the CSAE,2005(3):6-11.

[8] 尚松浩.土壤水分模拟与墒情预报模型研究进展[J].沈阳农业大学学报,2004(Z1):455-458.Shang S H.Advances in soil moisture simulation and forecasting models[J].Journal of Shenyang Agricultural University, 2004(Z1):455-458.(inChinese)

[9] 韩红亮,缴锡云,陆敏,等.蔬菜大棚墒情预报的衰减指数平滑模型[J].灌溉排水学报,2013,32(1):131-134.Han H L,Jiao X Y,Lu M,et al.Attenuation index smoothing model for predicting soil moisture in vegetable greenhouses[J]. Journal of Irrigation and Drainage,2013,32(1): 131-134.(inChinese)

[10] 安小宇,鲁奎豪,崔光照.基于改进樽海鞘优化BP神经网络的土壤墒情预测[J].中国农机化学报,2019,40(11): 124-130. An X Y,Lu K H,Cui G Z.Prediction of soil moisture based on BP neural network optimized by adaptive salp swarm algorithm[J].China Agricultural Machinery Chemistry News, 2019, 40(11):124-130.(inChinese)

[11] 冀荣华,张舒蕾,郑立华,等.基于多值神经元复数神经网络的土壤墒情预测[J].农业工程学报,2017,33(S1):126-131. Ji R H,Zhang S L,Zheng L H,et al.Prediction of soil moisture based on multilayer neural network with multi-valued neurons[J].Transactions of the CSAE,2017, 33(S1): 126-131.(in Chinese)

[12] 杨绍辉,王一鸣,郭正琴,等.ARIMA模型预测土壤墒情研究[J].干旱地区农业研究,2006(2):114-118. Yang S H,Wang Y M,Guo Z Q,et al.Research on soil moisture forecast based on ARIMA model[J].Agricultural Research in Arid Regions,2006(2):114-118.(inChinese)

[13] 李军,张和喜,蒋毛席,等.基于ARIMA模型的贵州省黄壤墒情预测研究[J].人民黄河,2010,32(8):73-75. Li J,Zhang H X,Jiang M X,et al.Prediction of yellow soil moisture in Guizhou province based on ARIMA model[J]. Yellow River,2010,32(8):73-75.(inChinese)

[14] 李芳花.黑龙江省半干旱地区土壤水分遥感监测技术研究及应用[D].长春:吉林大学,2006. Li F H.Study and application for soil moisture monitor using remote sensor technology in the semiarid area of Heilongjiang province[D].Changchun:Jilin University, 2006. (inChinese)

[15] Lewin J.Simple soil water simulation model for assessing the irrigation requirements of wheat[J].Israel J Agr Res, 1972,22(4):201-213.

[16] 粟容前,康绍忠,贾云茂,等.汾河灌区土壤墒情预报方法研究[J].中国农村水利水电,2005(10):92-95. Su R Q,Kang S Z,Jia Y M,et al.Preliminary study on soil moisture forecast in fen river irrigation district[J].China Rural Water Conservancy and Hydropower,2005(10): 92-95. (inChinese)

[17] 唐春燕,申双和,杜筱玲,等.南方土壤墒情变化规律及动态预报研究:以江西省南康市、湖口县为例[J].江西农业大学学报,2013,35(5):1082-1089. Tang C Y,Shen S H,Du X L,et al.The changing law and dynamic forecast of soil humidity in Nankang and Hukou counties, Jiangxi province [J].Journal of Jiangxi Agricultural University,2013,35(5):1082-1089.(inChinese)

[18] 申慧娟,严昌荣,戴亚平.农田土壤水分预测模型的研究进展及应用[J].生态科学,2003(4):366-370. Shen H J,Yan C R,Dai Y P.Progress and application of soil moisture monitoring and forecasting models[J].Ecological Science,2003(4):366-370.(inChinese)

[19] 马晓刚.基于秋季降水量的春播关键期土壤墒情预测[J].中国农业气象,2008,29(1):56-57. Ma X G.Forecast of soil moisture content during critical period of spring sowing based on precipitation in last autumn[J].Chinese Journal of Agrometeorology,2008,29(1): 56-57.(inChinese)

[20] 李清河,徐军,高婷婷,等.干旱荒漠区EC-5土壤水分传感器的校准和应用[J].中国农业气象,2012,33(1):54-58. Li Q H,Xu J,Gao T T,et al.Calibration of EC-5 soil moisture sensors and its application in arid desertificated area[J]. Chinese Journal of Agrometeorology, 2012,33(1): 54-58.(inChinese)

[21] Xiao D Q,Feng J Z,Wang N,et al.Integrated soil moisture and water depth sensor for paddy fields[J].Computers and Electronics in Agriculture,2013,98:214-221.

[22] 刘敏,王亮亮,蔡秋鹏.FDR和TDR测定几种典型土壤含水量的对比分析[J].水利信息化,2016(6):32-36. Liu M,Wang L L,Cai Q P.Comparative analysis of several typical soil's water content measuring with FDR and TDR[J].Water Resources Informatization,2016(6):32-36.(inChinese)

[23] 李泳霖,王仰仁,武朝宝,等.水分传感器埋设深度及个数对墒情精度的影响[J].节水灌溉,2019(1):87-91. Li Y L,Wang Y R,Wu C B,et al.The influence of the depth and amount of soil moisture sensors on the accuracy of soil moisture content [J].Water Saving Irrigation,2019(1): 87-91. (inChinese)

[24] 卞艳丽,曹惠提,杨一松,等.田间土壤墒情预报模型关键参数确定方法研究[J].人民黄河,2012,34(10):103-104. Bian Y L,Cao H T,Yang Y S,et al.Study on method of determining key parameters in soil moisture model for forecast of field[J].Yellow River,2012,34(10):103-104.(inChinese)

[25] Mahmood R,Hubbard K G.An analysis of simulated long-term soil moisture data for three land uses under contrasting hydroclimatic conditions in the Northern Great Plains[J].Journal of Hydrometeorology,2004,5(1):160-179.

[26] 王仰仁,孙书洪,叶澜涛,等.农田土壤水分二区模型的研究[J].水利学报,2009,40(8):904-909. Wang Y R,Sun S H,Ye L T,et al.Two-zone model for simulating field soil moisture[J].Journal of Hydraulic Engineering,2009,40(8):904-909.(inChinese)

[27] Cho T,Kuroda M.Soil moisture management and evaluation of water-saving Irrigation on farms[J].Journal of Irrigation Engineering and Rural Planning,1987(12):25-40.

[28] 王笑影.农田蒸散估算方法研究进展[J].农业系统科学与综合研究,2003(2):81-84. Wang X Y.Study of the estimating methods for evapotranspiration in farmland[J].Agricultural System Science and Comprehensive Research,2003(2):81-84.(inChinese)

[29] Allen R G,Pereira L S,Raes D,et al.Crop evapotranspiration guidelines for computing water requirements[M]. FAO Irrigation and Drainage Paper,1998.

[30] 李宝五.基于水量平衡的玉米土壤墒情预报研究[D].郑州:华北水利水电大学,2017. Li B W.The forecast for soil moisture based on soil-water balance model in summer maize[D].Zhengzhou:North China University of Water Conservancy and Hydropower, 2017.(inChinese)

[31] 张雪飞.水量平衡模型在德国奥斯纳布吕克地区和安徽淮北地区对墒情预测的应用研究[D].合肥:安徽农业大学,2013. Zhang X F.Water balance model of soil moisture prediction research in Osnabrueck,Germanv and Huaibei, Anhui[D]. Hefei :Anhui Agricultural University,2013.(inChinese)

[32] 牛宏飞,张钟莉莉,孙仕军,等.土壤墒情预测模型对比[J].中国农业大学学报,2018,23(8):142-150. Niu H F,Zhang Z L L,Sun S J,et al.Comparative study on soil moisture content prediction model[J].Journal of China Agricultural University,2018,23(8):142-150.(in Chinese)

Dynamic Modeling and Prediction of Soil Moisture Based on Real-Time Water Content Data

WANG Tie-ying1, WANG Yang-ren1，ZHAN Guo-long2, NIU Shao-qing2, YAO Li1

(1.School of Hydraulic Engineering, Tianjin Agricultural University, Tianjin 300392, China；2.Tianjin Dayu Water-Saving Irrigation Technology Research Institute, Tianjin 301712)

Real-time and accurate prediction of moisture content is to carry out irrigation forecasts, and to achieve precise management of farmland water, which is an important measure to improve water efficiency. Based on the principle of water balance in the root zone (0−60cm soil layer), the crop transpiration and water flux at the lower interface of the root zone are linearized by using the Taylor series. On this basis, a dynamic soil moisture prediction model was constructed with the real-time average soil moisture content of the root zone as an independent variable. The real-time monitoring data (soil moisture content at 30cm and 60cm below the ground surface) of the wireless soil moisture monitoring system (including three monitoring points) in Xilv Village, Wuqing District, Tianjin City are used, and 5 days, 10 days, 15 days and 20 days are selected as the modeling series length respectively, and regression analysis is performed to determine the model parameters. The prediction accuracy of soil moisture was analyzed, using the two forecast periods of 10 days and 15 days. The results showed that: (1)the real-time prediction model fits well, and the deterministic coefficients under the condition of the three modeling series length can above 0.80 (the number of samples are all greater than 550).(2) The relative error of 15 days modeling series is the smallest.(3) Under the conditions of 15 days modeling series length, 15 days prediction period, and 10% relative error limit value, the moisture prediction pass rates of the three monitoring points reached 98%, 100% and 89%, respectively. It can be seen that the real-time moisture prediction model proposed by the research has high prediction accuracy, which is convenient for modeling and analysis, and provides a new method for soil moisture prediction.

Soil moisture; Dynamic modeling; Sensor; Water balance; Soil moisture prediction

10.3969/j.issn.1000-6362.2021.01.002

王铁英,王仰仁,战国隆,等.基于实时含水率数据的土壤墒情动态建模及预测[J].中国农业气象,2021,42(1):13-23

2020−08−25

国家自然科学基金项目（51779174）；天津市农业科技成果转化与推广项目（201701150）；天津市科技支撑重点项目（18YFZCSF00650）

王仰仁，教授，主要从事灌溉排水技术研究，E-mail：wyrf@163.com

王铁英，E-mail：2696984426@qq.com