机架模型下指向误差数据的筛选与分析
2021-01-19胡晓炜朱庆生
胡晓炜,朱庆生
(1. 中国科学技术大学,安徽 合肥 230026 ;2. 中国科学院南京天文仪器有限公司,江苏 南京 210042)
在天文望远镜的指向误差修正方面,文[1]建立了机架模型,经修正后的指向精度优于5″;文[2]对静态指向模型的基本参数进行了讨论,通过逐步回归分析,确定了码盘零点差、度盘偏心误差等误差源作为显著回归因子;文[3]对比了球谐函数模型和水平式望远镜指向模型,并通过水平式望远镜观测验证了模型的有效性。在射电望远镜的指向性能改进上,文[4]通过修正轨道高差造成的指向偏差,提高了天线整体的指向精度。本文通过软件方式修正指向误差,对机架模型误差数据的获取及系数求解做了说明,并通过残差分析的方法筛选指向误差数据,计算均方根误差(Root Mean Square Error, RMSE)以验证模型对优化后数据的内符合精度,排除找星错误等误操作对修正结果的影响,提高拟合精度。在此基础上分析加密测量点数对指向修正精度的影响,并说明了分次获取的误差数据,残差检验后可合并处理。使用本文方法对1 m人造卫星激光测距望远镜和地基激光发射望远镜获取的指向误差数据进行分析,修正精度均得到有效提高。
1 指向误差影响因素分析
天文望远镜在设计、加工、制造、装配等环节,由于多种因素引入指向误差,导致望远镜主光轴显示到达的位置与目标星实际位置存在偏差,在跟踪过程中不能准确指向卫星的预报位置。这些因素主要包括机架的制造与安装误差、轴系倾斜、轴间不正交、重力变形、镜筒与光学系统的弯沉[5]、光栅编码器误差、视准轴误差等。指向误差一般用均方根误差表示。
指向误差的修正可采用硬件修正和软件修正两种方法。硬件修正指在机械和光学系统设计加工、装调过程中,采用轴系校准、视轴校准、光栅编码器测角组件校准等方法减小误差。但望远镜装调结束后难以通过硬件修正减小误差,且随着运动部件的磨损,硬件修正效果大打折扣,修正效果有限且费用较高。软件修正是提取影响望远镜指向误差的各个因素,利用系统误差重复性的特征建立数学模型并通过计算机软件修正。
通过对望远镜机械系统的分析可以估计不加修正前的误差量,这部分误差为系统误差。就地平式望远镜而言,指向误差中系统误差较大,随机误差较小,由于系统误差与望远镜轴系的角度有关,可以建立高度误差ΔH和方位误差ΔA的拟合模型。
望远镜在指向与跟踪前需要建立指向误差模型,通过回归分析确定拟合参数。在运行时,计算机实时计算望远镜在当前指向处的系统误差估计值,并对光栅编码器反馈的位置进行修正,可消除指向误差中的系统误差,大幅提高望远镜的指向精度和盲测的跟踪精度,美国的SLR2000经模型修正后指向误差可小于1″。
望远镜指向误差修正过程包括:(1)恒星选取;(2)获取误差数据;(3)建立指向误差模型;(4)计算模型参数;(5)验证模型符合度;(6)在望远镜控制程序中导入修正系数并实时修正。
2 常用指向误差模型
2.1 球谐函数模型
采用球谐函数多项式对地基望远镜指向误差进行拟合的误差模型称为球谐函数模型,它可应用于任何机架结构的望远镜,通过对基准面为球面误差进行拟合,方法简单,可拟合各种误差,对地平式望远镜和赤道式望远镜能达到较高的内符合精度。但模型参数较多且没有实际物理意义,参数之间相关性大,模型不稳定[6],重新测得数据后,求出的模型参数变化大。
2.2 基本参数模型
对望远镜的静态指向误差及基本参数逐步回归分析以确定显著回归因子。由于导致指向误差的因素较多且可能存在相关性,通过逐步回归分析可将误差源中的不显著因子剔除,确保模型中的参数项必须存在且不可替代。分析思路是将误差源逐个引入,每引入一个变量,对模型中的原有变量逐个检验,将不显著的因子删除,重复该步骤,直至添加所有误差源。此时,回归模型中的所有误差源对修正系数都是显著的,因为经过逐步回归分析,参数项较少且参数之间相关性小,模型较为稳定[7]。但需根据望远镜的机架结构引入其他参数,设计不同的模型并验证残差,过程复杂,拓展性差。
2.3 机架模型
机架模型也称为转台模型,常用于地平式望远镜,通过对望远镜机架结构分析建立模型。全模型共有24项参数,通过对参数间的相关性回归分析及试验,保留19项参数,其中方位轴参数有11项,高度轴参数有10项(方位轴南北向倾斜和方位轴东西向倾斜为共同参数),这些参数均有实际的物理意义,表1和表2分别为机架模型方位轴和高度轴各项参数。
机架模型的表达式为
ΔA=a1-a2cosAtanH-a3sinAtanH+a4secH-a5tanH+a6sinA+a7cosA+a8sin2A+
a9cos2A+a10sin2AsecH+a11cos2AsecH,
(1)
ΔH=b1+b2sinA-b3cosA+b4cotH+b5sinA+b6cosA+b7HsinA+b8HcosA+b9sin2A+
b10cos2A.
(2)
机架模型是对基本参数模型的扩展,具有更高的精度,符合度优于基本参数模型。由于机架模型加入了更多的参数,增大了参数间的相关性,因此没有基本参数模型稳定[8]。
3 误差数据获取与机架模型系数求解
望远镜指向模型修正分为零点校正、指向误差测定和模型系数求解3个模块,将修正系数载入控制程序,在恒星和卫星的指向与跟踪中实时修正。本文基于地基激光发射望远镜,选用机架模型修正指向误差。
3.1 测定码盘零点偏差
通过FK5星表或星图软件使望远镜指向任意一颗恒星(避免指向双星系统,条件允许时选北极星可便于跟踪,避免引入更多误差),手动将该星调到CCD中心,用码盘测得的方位/高度值减去该星的理论方位/高度值,即为码盘的零点偏差。通过这一步骤,修正码盘零点和坐标系零点之间的偏差。
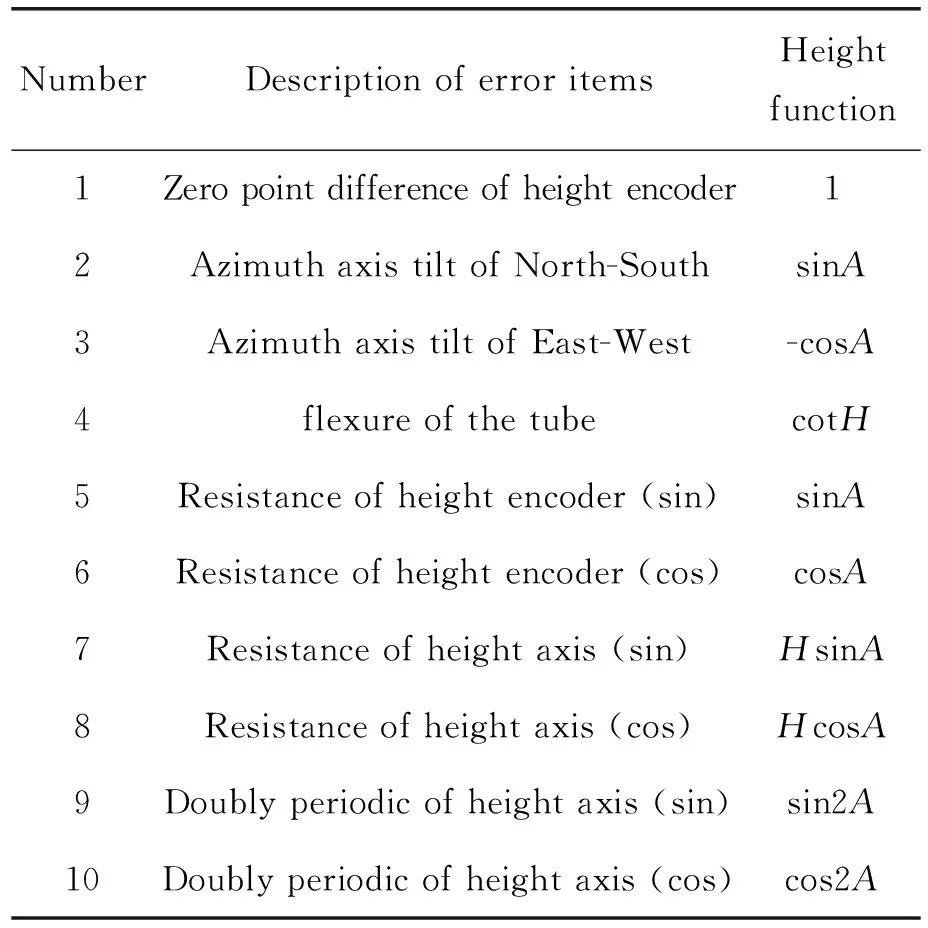
表2 机架修正模型参数表(高度轴)
3.2 划分天区,获取数据
在晴夜中,根据拟获取的测试数据组数均匀划分天区,在每个分区内选定一颗亮度适中的恒星(太亮容易曝光过度,使获取的误差数据不准确,太暗可能与周围的恒星混淆)。此时有两种方法可以获得指向误差数据:(1)根据该星偏离CCD中心的脱靶量和像素的空间分辨率,计算望远镜在该空间指向处的指向误差;(2)手动将目标星调整到相机成像中心,该方法能避免方位轴像素分辨率随高度角变化带来的影响,有效提高测量精度。通过测量星点在CCD上偏移一定像素对应的望远镜转角,可以测定像素分辨率。经试验,在高度角为0°时,方位像素分辨率见表3。高度角H处,方位的像素分辨率为(0.466cosH)″。因此,采用第2种方法记录误差数据(方位、高度、方位误差、高度误差)。试验共测得66组数据。
3.3 求解指向模型系数
利用MATLAB对获取的误差数据进行处理,计算修正系数。误差数据包含4项,分别为方位角AZi、高度角Hi、方位偏差ΔAZi、高度偏差ΔHi(方位、高度以弧度表示,偏差数据以角度表示,共测得N组数据,i=1, 2, …,N),将其导入MATLAB中,构造4组一维列向量,代入机架模型的方位函数与高度函数,得到修正系数矩阵A,通过最小二乘法求解,可求得修正系数向量B。推导过程如下。
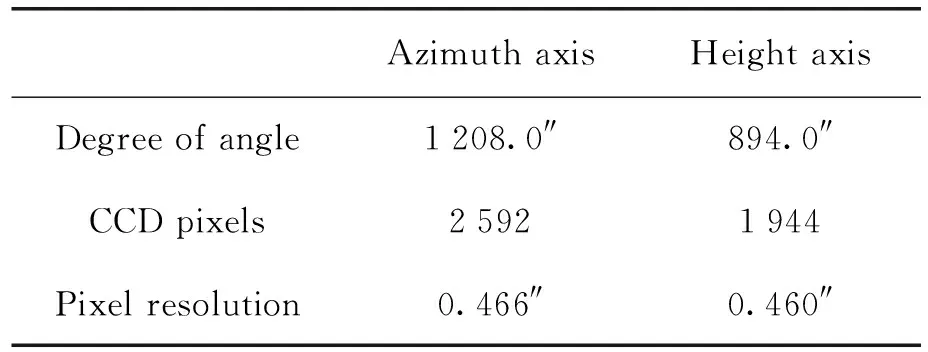
表3 CCD像素分辨率测量表Table 3 CCD pixel resolution measurement table
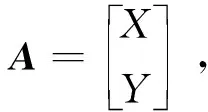
X=[1 0-cos(AZ).×tan(H)-sin(AZ).×tan(H)sec(H)-tan(H)sin(AZ)cos(AZ) 0 sin
(2.×AZ) cos(2.×AZ) 0 0 0 0 sin(2.×AZ).×sec(H)cos(2.×AZ).×sec(H) 0 0] ,
(3)
Y=[0 1 sin(AZ)-cos(AZ) 0 0 0 0 cot(H) 0 0 sin(AZ)cos(AZ)H.×sin(AZ)H.×cos
(AZ) 0 0 sin(2.×AZ)cos(2.×AZ)].
(4)
采用多项式曲线拟合,拟合曲线方程为19阶多项式。测试数据共66组,系数矩阵A为132 × 19,误差矩阵E为132 × 1,
(5)
用矩阵形式可以表示为
E=AB,
(6)
B为待求解的修正系数向量[b19,b18, …,b1]T,在方程两边左乘AT,得到
ATE=ATAB,
(7)
在(7)式两边同乘ATA的逆矩阵,有
B=(ATA)-1ATE,
(8)
上式右半部分各项均已知,可求解得到修正系数向量B。
在望远镜的基座、重力分布未发生较大变化的情况下,一次误差测定可长期使用。
4 误差数据分析及模型符合度验证
在指向模型数据处理的过程中,修正系数的拟合精度受单次观测统计量的影响。当出现目标星识别错误、基座振动等情况时,测量的误差值会大幅偏离真实误差值。异常的观测数据在图形上呈现孤立型,偏离由大多数数据组成的分布趋势,需要剔除这些数据,减小对拟合精度的影响。
通过残差分析的方法剔除偏离大的数据,从而保证实验数据的精确度。从上节的求解模型中提取方位误差并单独求解,由(1)式可知,方位修正系数共11项,若要求解这11个系数,最少需要11组方程。试验共获取66组数据,可构建66组方程,相应地有66个残差。本文中,第i组数据的残差ei
为该组的预测值y^i与观测值yi之差,即ei=y^i-yi。代入上节求解模型,有
e=3 600[(XB)-ΔAZ] ,
(9)
(9)式残差的单位为角秒(″),取残差95%置信区间,可得方位残差图,以此估计预测的误差与实际误差是否一致,从而验证所建模型的符合度,方位残差图如图1,(a)为95%置信区间,(b)为99%置信区间。图1的横坐标表示测试文件中数据的序号,纵坐标代表残差,即拟合值与实际测量值之间的差值,单位为″。从图1可以看出,残差随机分布在0点两侧,若残差的置信区间与0点相交,说明获取的指向误差数据能够较好地符合模型,若置信区间偏离0点,该组数据可视为异常数据,需要剔除。以方位残差95%置信区间为例,66组测试数据中有4组异常,需要剔除以提高模型的精度。
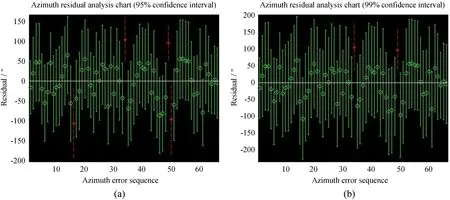
图1 方位残差分析图Fig.1 Azimuth residual analysis chart
为了验证指向模型对偏差数据的修正是否具有良好的精确度,本文采用均方误差(Mean-Square Error, MSE)作为评价指标,该指标可评价数据的变化程度,均方误差越小,说明模型描述数据越准确。均方误差表达式为
(10)
为了在数量级上更直观,可对均方误差开方,即均方根误差
(11)
以方位的指向误差为例,分别计算在不同组数下的均方根误差,如表4。
由于拟合方位误差需要确定11个系数,故最少需要11组测试数据。从表4可以看出,在一定范围内,增加测试组数能有效提高模型的符合度。当测试组数超过20组时,拟合数据的准确度反而随测试组数的增加而降低。因此,不经处理地增加测试组数并不能使拟合精度得到优化。添加新的误差数据后须经残差分析,剔除偏离较大的值才能降低拟合误差。
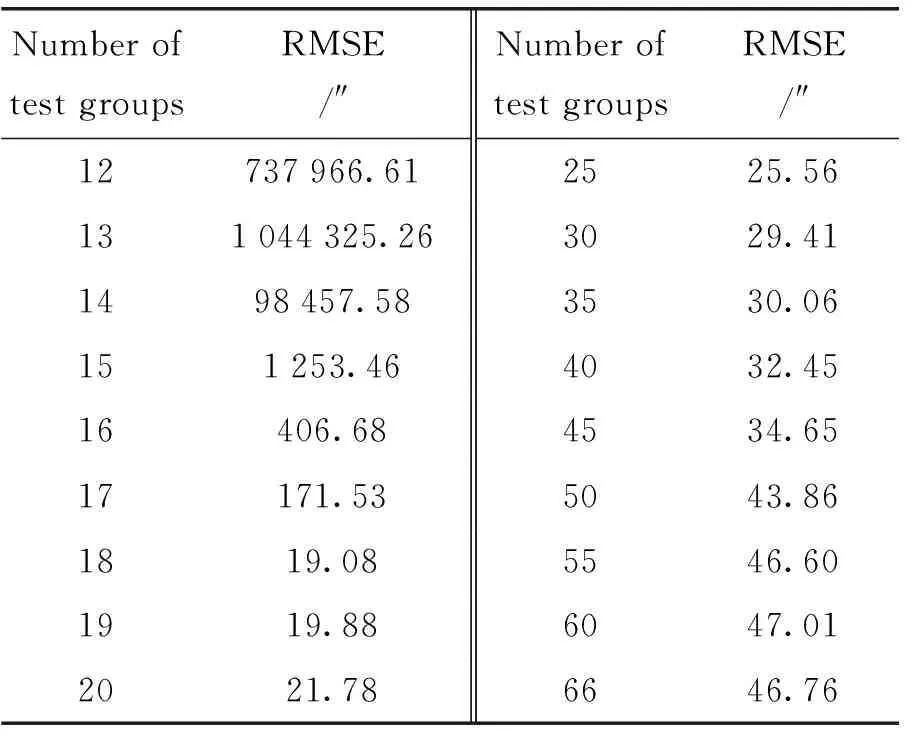
表4 不同数量测试组下计算的均方根误差(方位角)
在已获取指向误差数据的情况下,可通过残差分析,将残差95%置信区间与0点不相交的数据依次剔除,如图2,(a)为66组数据,(b)为62组数据,(c)为58组数据,(d)为54组数据,均取95%置信区间。计算剔除残差偏离数据后的均方根误差如表5、表6。
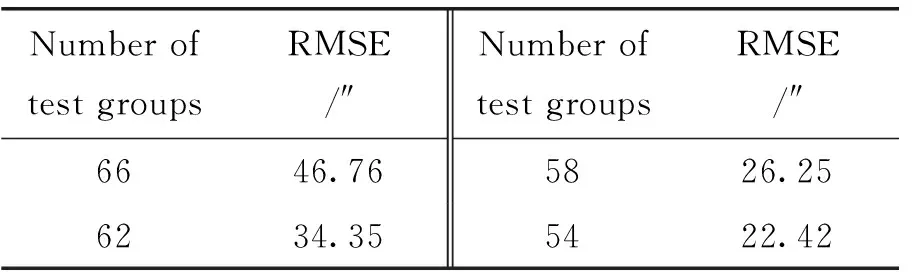
表5 剔除残差偏离数据后的均方根误差(方位角)
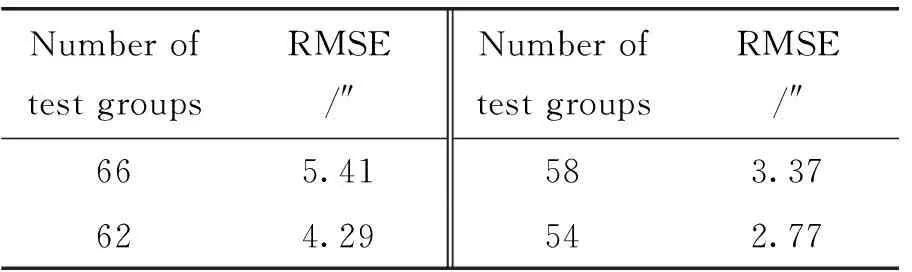
表6 剔除残差偏离数据后的均方根误差(高度角)
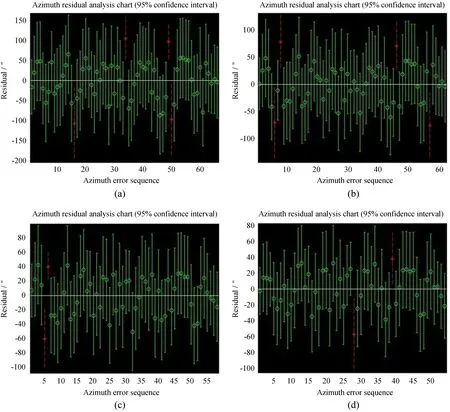
图2 剔除部分偏离较大数据后的残差分析图(方位角)Fig.2 Residual analysis chart after removing some value with large deviation (azimuth)
由(2)式可知,高度修正系数共有10项,故拟合高度误差至少需要10组数据。同理,对高度方向做残差分析,图3为残差分布直方图,横坐标表示残差,纵坐标表示某一残差范围的数据组数,由图3可以看出,高度残差近似服从正态分布。剔除部分偏离较大数据后的残差分析见图4,(a)为66组数据,(b)为62组数据,(c)为58组数据,(d)为54组数据,均取95%置信区间。
我们使用乌鲁木齐的地基激光发射望远镜做试验,在0°~360°范围内选择60颗恒星,测量指向误差数据(恒星指向数据的方位-高度分布如图5),删除残差偏离较大的数据点后,两轴均方根误差如表7、表8,相应残差分析图如图6、图7,(a)为60组数据,(b)为56组数据。
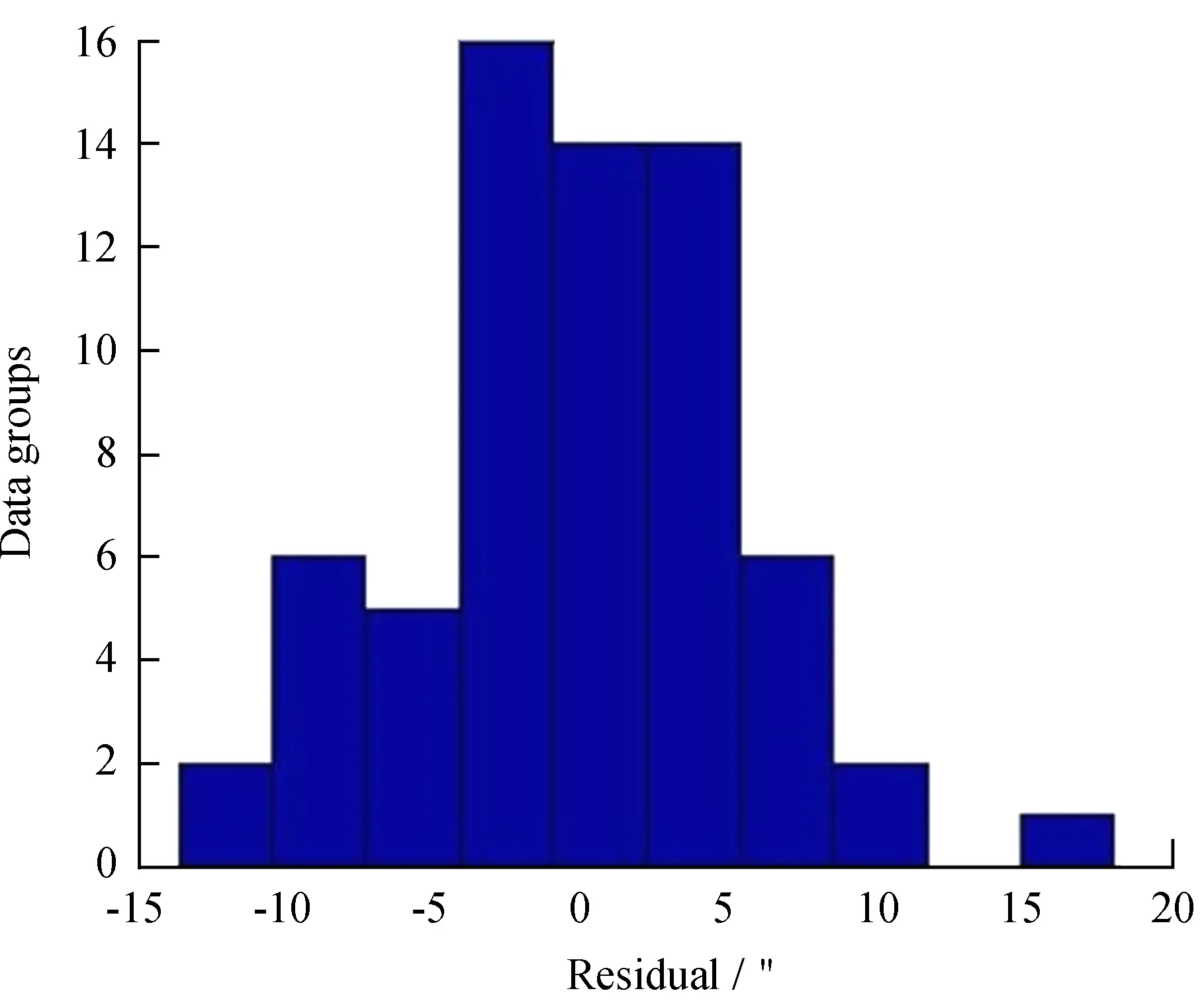
图3 高度角残差数据分布Fig.3 Height residual data distribution
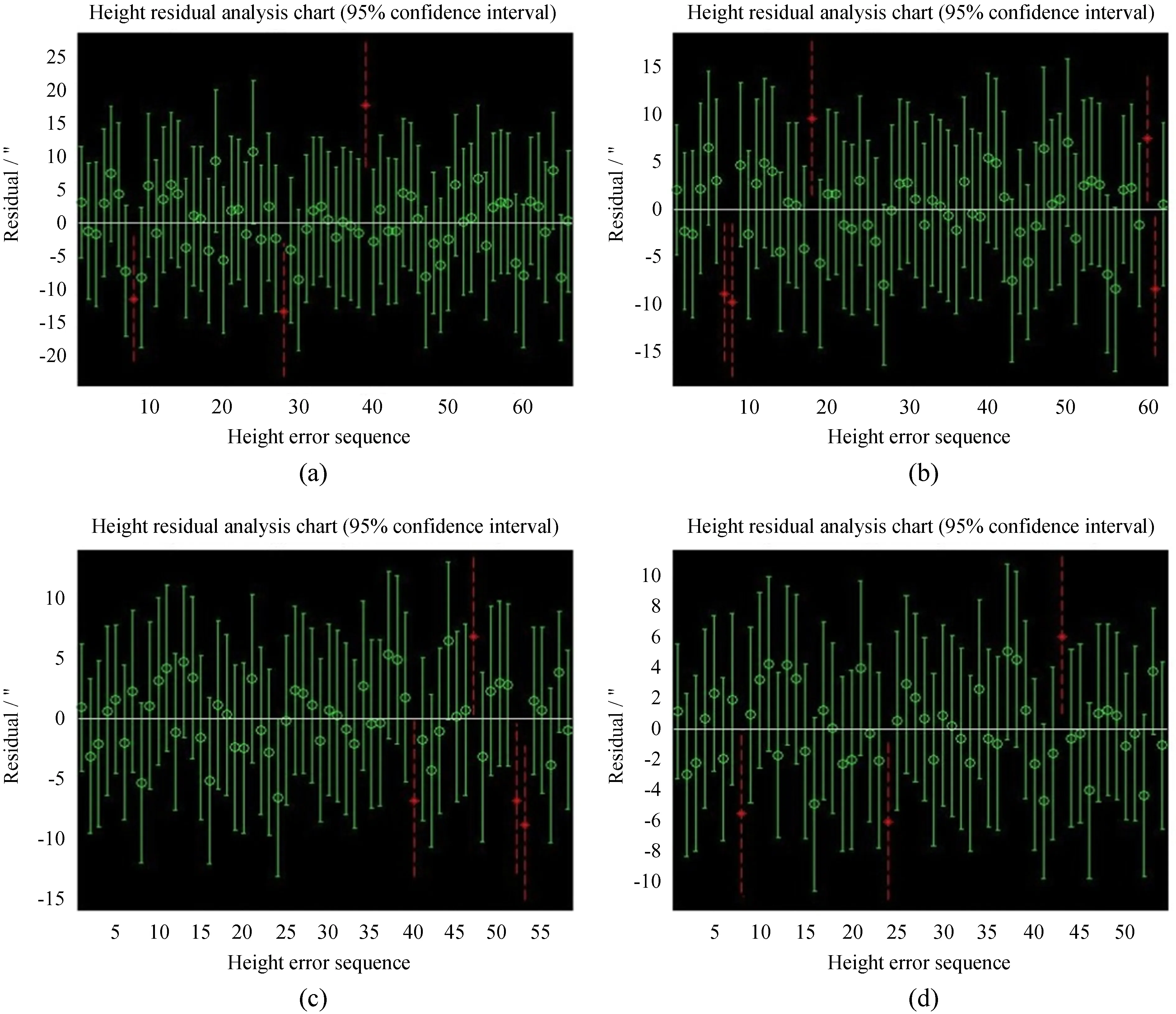
图4 剔除部分偏离较大数据后的残差分析图(高度角)Fig.4 Residual analysis chart after removing some value with large deviation (height)
表9为应用机架模型对位于乌鲁木齐的地基激光发射望远镜计算的两轴指向误差修正系数。第1组系数由原始的恒星指向数据计算得出(共60个数据点),两轴误差均方值分别为9.46″和18.47″。第2组系数由剔除部分残差偏离较大的指向数据计算得出(共56个数据点),两轴误差均方值分别为7.79″和11.39″。
试验获取了1 m人造卫星激光测距望远镜、地基激光发射望远镜的多组指向误差数据,通过计算分析得出结论:剔除残差偏离较大的数据后的测试组能够有效提高指向修正数据的拟合精度。
在外界环境未发生明显变化的前提下,指向误差数据可分次获取(可将分批获取的数据合并,使用残差图分析,若残差集中在95%置信区间内且未出现断层,可判定外部环境未发生明显变化),添加新的测试数据时,要保证添加后测试组的均方根误差小于原有测试组的均方根误差,才能提高指向模型对误差数据描述的准确度。
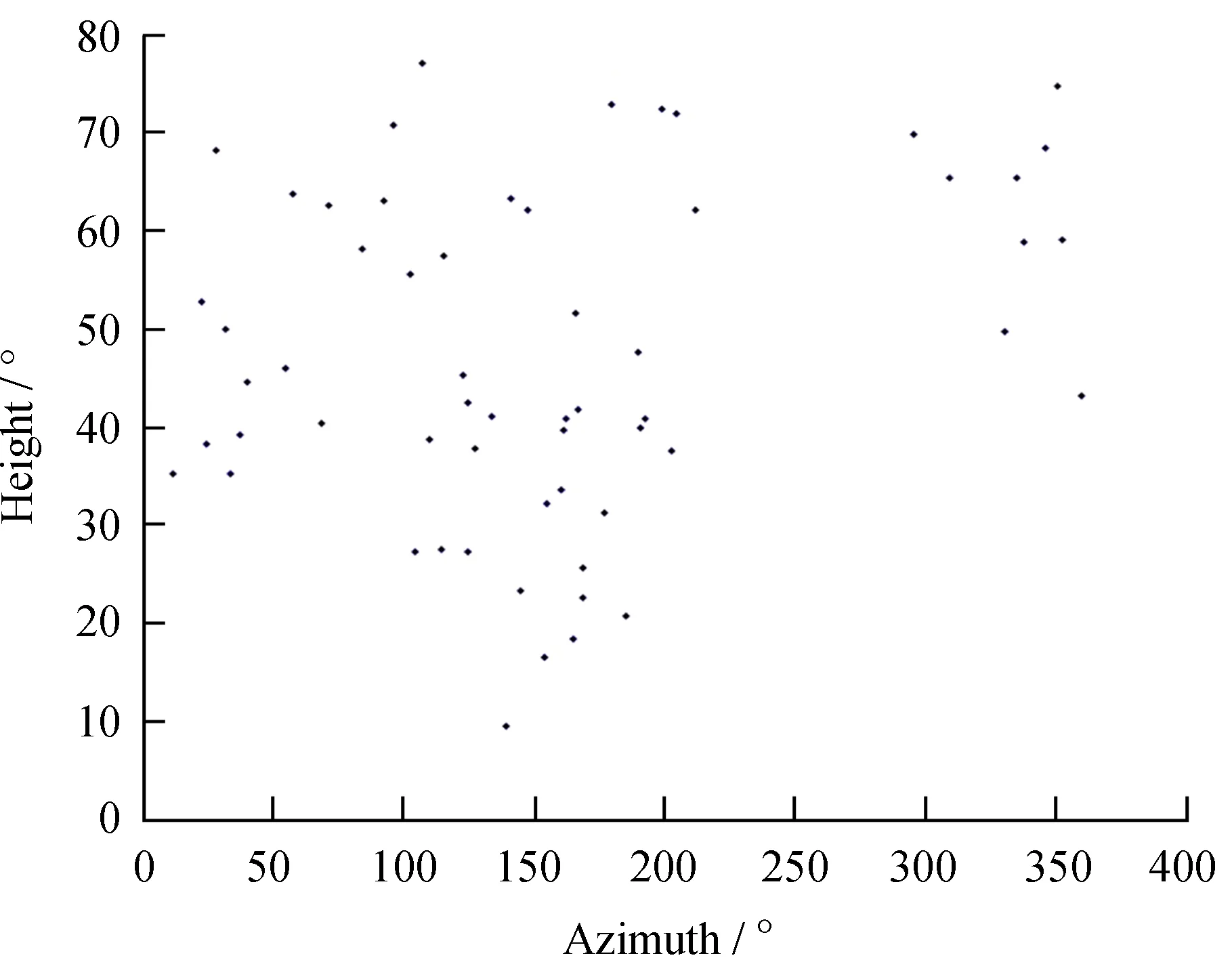
图5 恒星指向数据的方位-高度坐标分布图Fig.5 A-O-E coordinate distribution of star pointing data
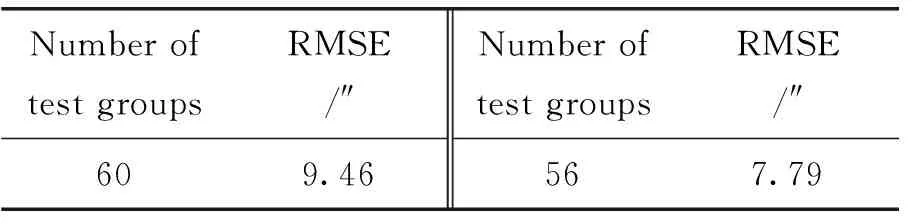
表7 剔除残差偏离数据后的均方根误差(方位角)

表8 剔除残差偏离数据后的均方根误差(高度角)
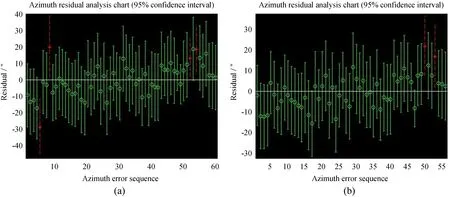
图6 剔除部分偏离较大数据后的残差分析图(方位角)Fig.6 Residual analysis chart after removing some value with large deviation (azimuth)
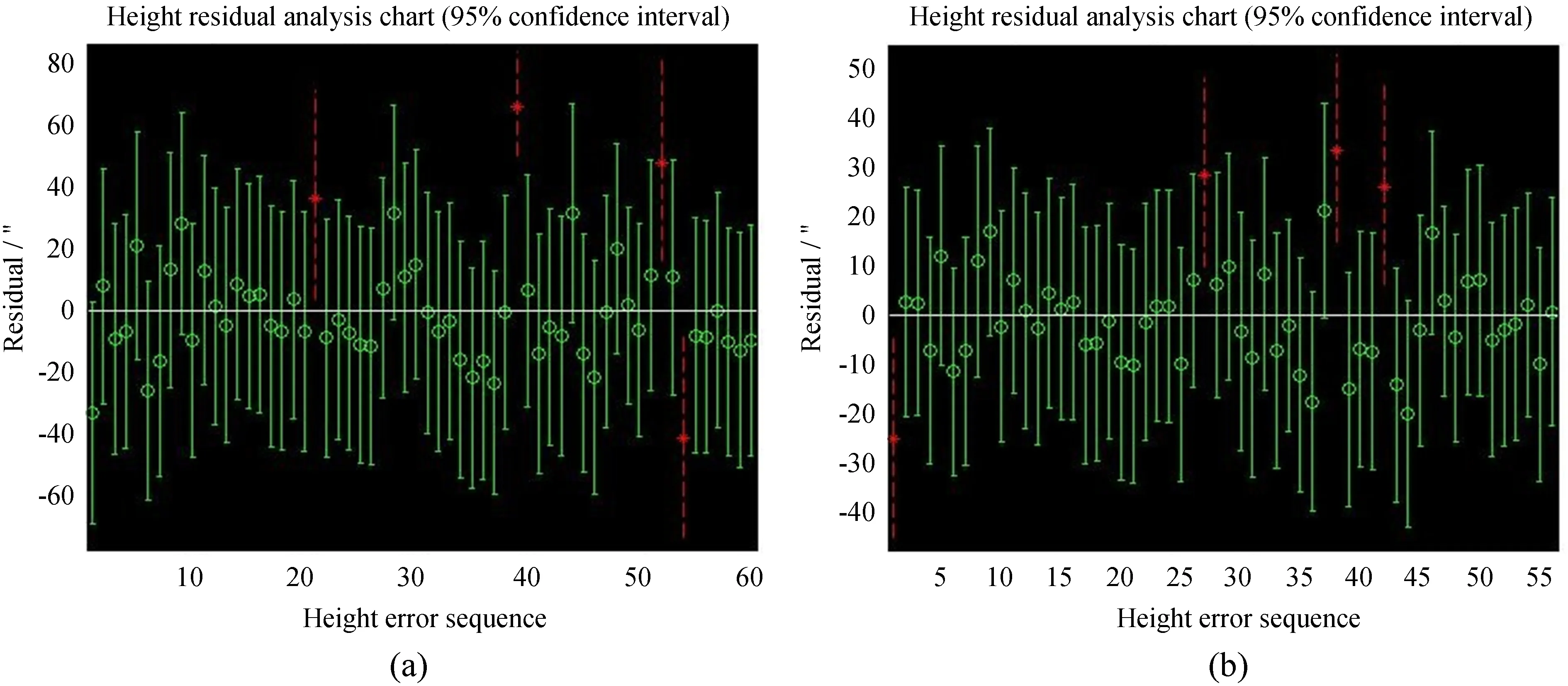
图7 剔除部分偏离较大数据后的残差分析图(高度角)Fig.7 Residual analysis chart after removing some value with large deviation (height)
通过多元线性回归检验机架指向修正模型对偏差数据拟合的精确度,如表10,R2为决定系数,其值越大,拟合程度越高。由表10可以看出,原始的66组测试数据拟合优度超过99%,误差拟合精度非常好。通过残差分析筛选数据后,拟合优度得到进一步提高。同样也可通过F检验的P值验证指向模型的有效性,当P< 0.001时,说明模型有效,由表10可看出,对于所列的测试组,F检验的P值远远小于0.001,说明指向模型能够很好地拟合偏差数据。
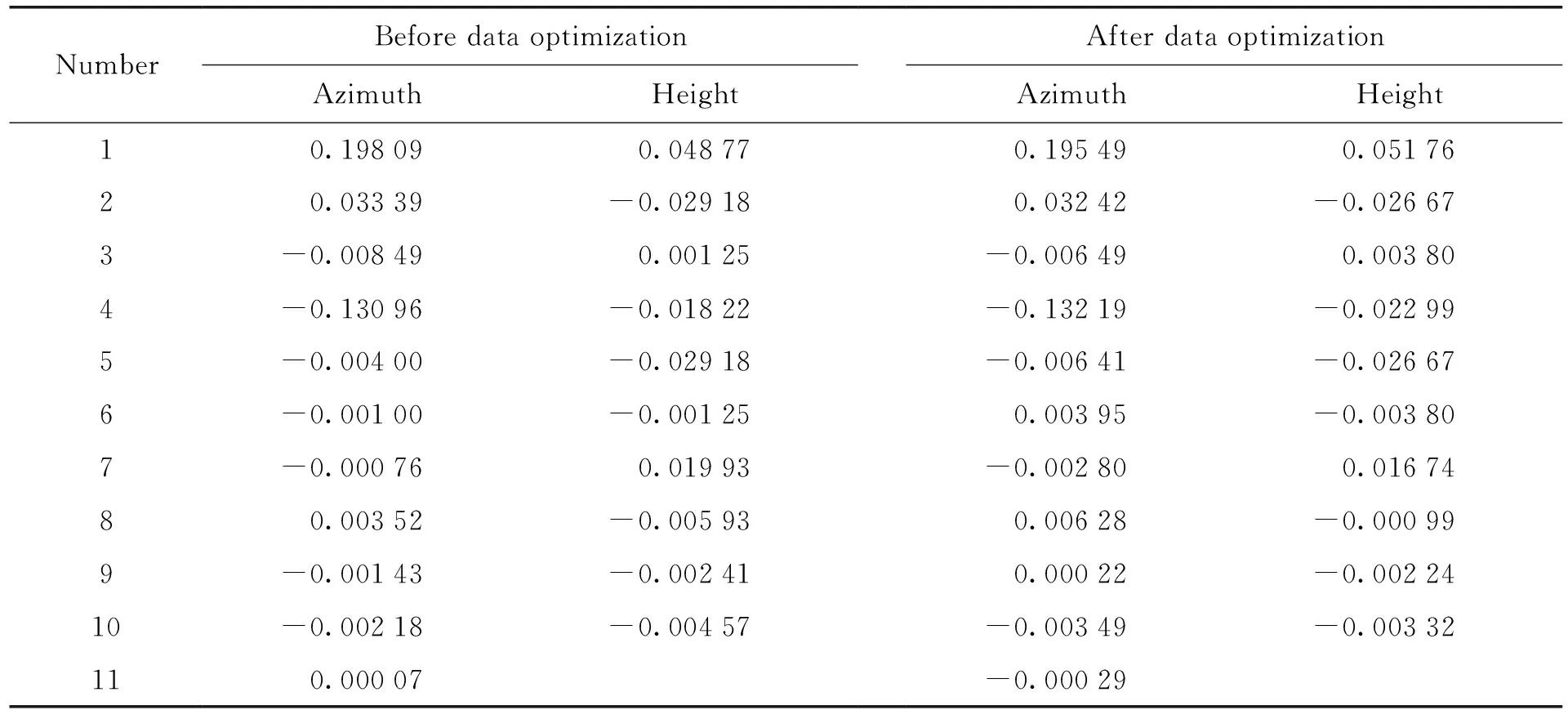
表9 应用机架模型计算的剔除残差偏离较大数据前后的修正系数对比
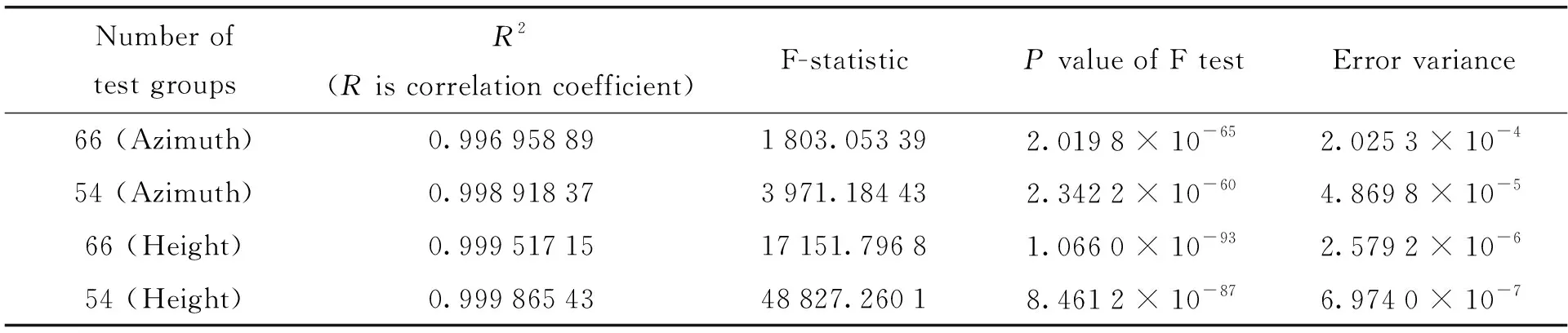
表10 机架模型检验表Table 10 Frame model inspection form
5 结 论
本文通过以上的试验与分析得出如下结论:
(1)对使用机架模型获取的指向误差数据,通过残差分析的方法剔除部分残差偏离较大的数据,能够有效提高指向修正精度。但随着数据组的不断优化,精度提高的幅度逐步减小。
(2)指向误差数据可分次获取,增加新的测试数据后,可使用残差图判定外部环境有无明显变化。若增加数据后,测试组的均方根误差小于原有测试组的均方根误差,能够提高修正精度。
