基于多重网格的射电源条纹搜索算法研究*

孙晓彤，童 力，郑为民,4，余 赟

(1. 中国科学院上海天文台，上海 200030；2. 中国科学院大学，北京 100049；3. 中国科学院射电天文重点实验室，江苏 南京 210008；4. 上海市导航定位重点实验室，上海 200030)

甚长基线干涉测量是20世纪60年代后期发展起来的一种射电干涉技术，具有高分辨率、高精度的特点，在天文观测、大地测量和深空探测等领域得到了广泛应用[1]，它的基本工作方式是位于基线两端的天线接收射电源辐射的电磁波，相关处理机利用干涉原理从实测数据中得到时延以及时延变化率，进一步获取射电源和有关基线的位置等信息。因此，快速、准确地获得射电源的干涉条纹，对甚长基线干涉测量的数据处理至关重要。

相关处理机是甚长基线干涉测量技术的核心数据处理设备，预报时延模型与实际时延的误差直接影响干涉条纹的处理效果，因此，处理机对所需预报时延模型有很高的精度要求。但在实际数据处理时，地球模型误差、大气模型误差、仪器误差以及台站坐标误差等都可能导致时延模型不准确甚至无法引导处理机正常工作。在常规地面甚长基线干涉测量中，由于台站坐标较稳定，可以通过预先计算获取预报时延模型与实际时延之间的误差，然后经过反复尝试获得准确的干涉条纹，在观测过程中通常不需要再次进行搜索。但对于空间甚长基线干涉测量，观测系统和轨道不稳定，误差随时变化，与地面甚长基线干涉测量有较大区别，因此，无法通过预先计算对时延模型进行一次性修正。目前，针对探测器信号的无时延模型条纹搜索研究较为成熟，上海天文台在这一领域取得了大量研究成果，解决的主要思路是利用探测器测控信号自身的特征设计条纹搜索算法[2]。但由于射电源信号是高斯白噪声信号，无法直接利用信号特征进行条纹搜索。在实际数据处理过程中，无时延模型的射电源条纹搜索往往采用半人工的方式，主要依赖操作人员的经验，这种方式费时费力，难以满足未来空间甚长基线干涉测量的需求。因此，解决不依赖时延模型对射电源条纹进行搜索这一难题，对推动空间甚长基线干涉测量的应用具有重要意义。

针对无时延模型的射电源条纹搜索，本文提出了基于多重网格的射电源条纹搜索算法，能够在较大的时延和时延率平面内进行搜索，利用滑窗技术以及多重网格技术快速自动定位到精确的时延、时延率。

1 甚长基线干涉测量相关处理原理

甚长基线干涉测量观测台站接收的射电源信号经过变频、滤波和二次变频后，被划分成多个频率通道，经过采样、量化、编码后记录在磁盘上或通过网络传输到甚长基线干涉测量中心[3]。设台站1接收的信号为x1，台站2接收的信号为x2，两台站信号之间满足

x2=x1(t-τ)，

(1)

由于地球自转和射电源的相对运动，τ实际上是一个随时间变化的函数，在很短的时间Δt内τ可以近似为一次函数：

(2)

经过下变频后两台站的输出信号分别为

s1(t)=x1(t)e-j2πf0t，

(3)

s2(t)=x2(t)e-j2πf0t=x1(t-τ)e-j2πf0t，

(4)

其中，f0为天空频率。

将原始数据解码后，固定台站1信号，对台站2信号做时延补偿，设τs为搜索的补偿时延，它与实际时延τr之差为Δτs，用公式表示为

τs=τr-Δτs.

(5)

由于数据是以数字信号的形式存储，采样间隔ΔT，则τs由整数部分nΔT和小数部分τsf两部分组成：

τs=nΔT+τsf.

(6)

时延的补偿分为两部分：(1)在时域完成的整数比特补偿；(2)在频域完成的小数比特补偿。对台站2信号进行整数比特补偿后为[3]

s2(t-nΔT)=x2(t-nΔT)e-j2πf0(t-nΔT)

=x2(t-τr-τsf+Δτs)e-j2πf0(t-τr+τsf+Δτs).

(7)

(8)

进行傅里叶变换后得到其频谱S2(f)，完成小数比特补偿后得到

(9)

对台站1做傅里叶变换，得到两台站之间的互功率谱为

(10)

其中，φ1和φ2分别为台站1和台站2信号的原始相位。

通过上述分析可以看出，两台站互相关功率谱和补偿时延τs与实际时延的差值Δτs、补偿时延率

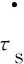
2 多重网格的条纹搜索

基线两端的天线接收由射电源辐射的电磁波，地球和射电源的相对运动使得电磁波的波前到达两个天线的时间差不断改变。干涉条纹只存在于同一波前信号的互相关功率谱中[4]。因此，只有将接收的两台站信号进行准确的时延和时延率补偿才可能得到射电源的干涉条纹。本文提出一种基于多重网格技术的算法，可以在无预报时延模型的情况下对射电源条纹进行搜索。

2.1 多重网格技术基本原理

多重网格的基本思想是建立多层次、不同尺寸的网格，通过这些网格在不同范围内搜索需要的目标值[5]。如图1，搜索空间划分为L层，每层网格由边长相同的单元格构成，单元格的边长称为搜索步长，每个单元格的结点表示不同的搜索值。在划分过程中，随着网层号的降低，网格尺寸减小，搜索精度提高。

通过对甚长基线干涉测量相关原理的分析可知，每一对补偿时延和补偿时延率与其互相关功率谱相对应。条纹搜索需要在时延-时延率平面中找出存在条纹的互相关功率谱对应的时延和时延率。将时延-时延率搜索平面划分网格，网格尺寸的大小决定了时延和时延率的搜索精度，最底层的网格尺寸由相关处理机的精度需求决定。

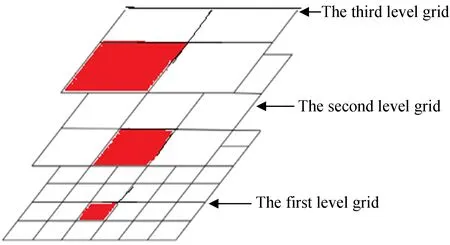
图1 多重网格示意图Fig.1 Schematic diagram of multiple grids

甚长基线干涉测量处理机对时延和时延率的补偿精度有很高的要求。时延补偿的精度必须满足[6]

(11)

其中，W为频率通道带宽；N为谱通道个数(FX 型处理机)或时延通道个数(XF型处理机)。

时延率的误差Δτ˙需要满足

(12)

其中，T为积分时间；f为观测频率。

若直接选取满足相关处理机精度要求的单一网格，相应的计算量极大，条纹搜索效率很低。为了提高搜索效率，采用粗网格定范围、细网格定终值的策略。首先选取较大的搜索步长，在粗网格的搜索平面内确定正确的时延和时延率补偿所在的范围，如图2(a)，通过计算确定正确的值落在图中红色区域，用于第2步精搜索，这一过程称为粗搜索。缩小搜索范围后，同时缩小网格以满足相关处理机的精度要求，如图2(b)，进而可以在细网格内搜索到更高精度的时延和时延率补偿，完成精搜索。

图2 网格操作示意图。(a)粗网格；(b)细网格Fig.2 Schematic diagram of grid operation. (a) Rough grid; (b) Fine grid

射电源信号的信噪比低，需要增加积分时间解决这一问题，但计算机对相关计算长度和傅里叶变换计算的长度都有限制[7]，通过对信号的分段处理可平衡两者之间的关系。在两路信号中，需要固定一路信号作为参照信号，对另一路信号进行分段处理，第1路信号与第2路信号每段进行相关处理即实现滑窗相关。信号滑窗操作方法如图3，将台站信号在搜索范围内以网格要求的搜索步长滑动，并在相关计算后记录互相关功率谱，提取相位后计算方差。

2.2 评估时延和时延率补偿结果的依据和方法

由(10)式可知，若补偿准确，互相关功率谱的相位与频率呈线性关系，斜率表示残余时延。如图4(a)表示时延和时延率补偿与实际时延和时延率相近的相位结果，补偿不准确的时延和时延率的相频图如图4(b)。

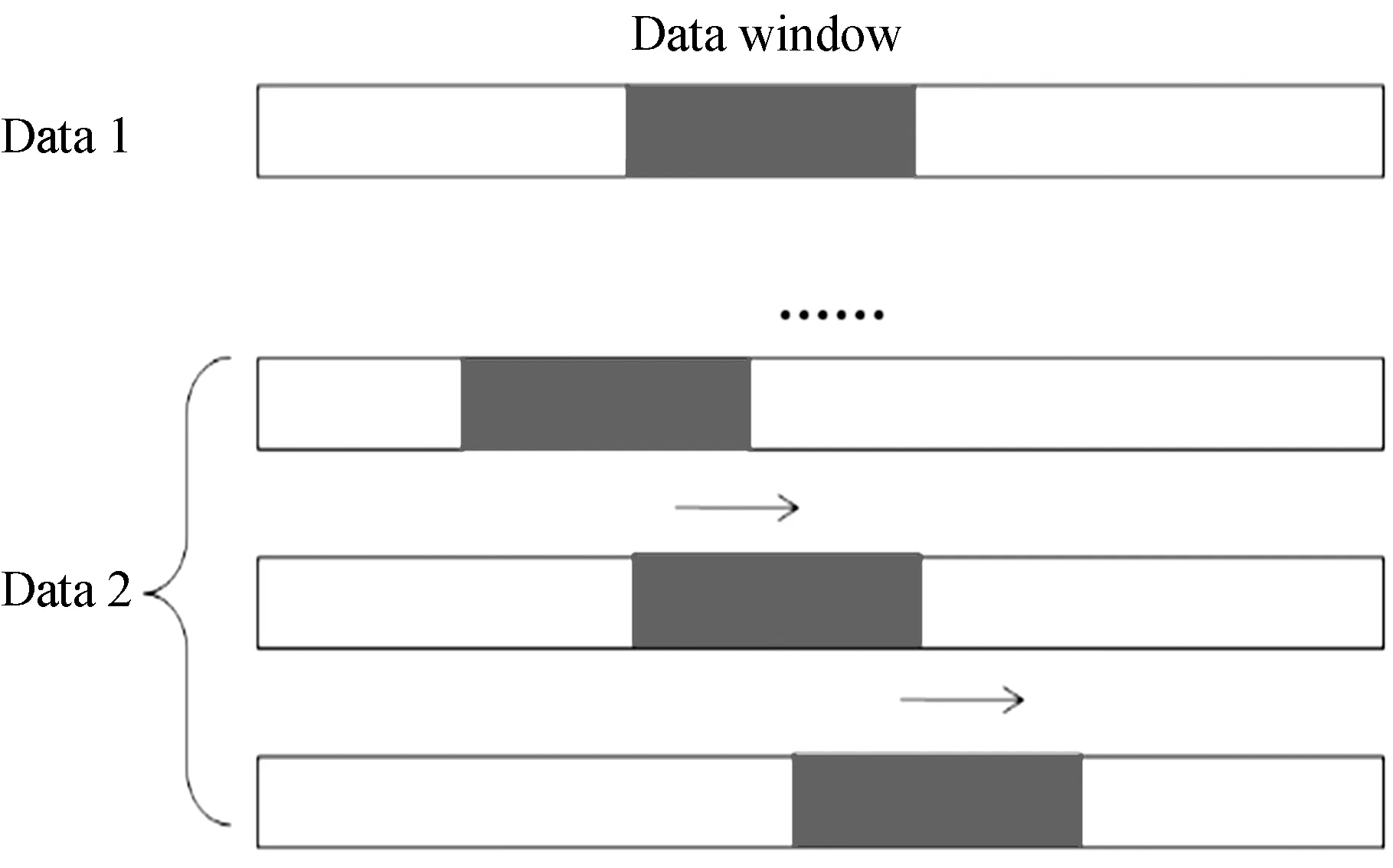
图3 滑窗操作示意图Fig.3 Schematic diagram of sliding window operation

从图4可以看出，互相关功率谱的相位弥散程度可以衡量时延、时延率补偿的准确性。补偿时延和时延率与实际时延和时延率误差小，相位弥散程度小；补偿误差大，相位弥散程度大。要度量相位的弥散程度需要先对相频图进行线性拟合，确定基准点的位置。采用最小二乘法进行线性拟合，如图4(a)。由于最小二乘的曲线拟合方法是通过最小误差的平方找到拟合结果，虽然补偿不准确的相频谱不具备线性关系，但仍然可以拟合出一条与真实数据距离最近的直线，如图4(b)。

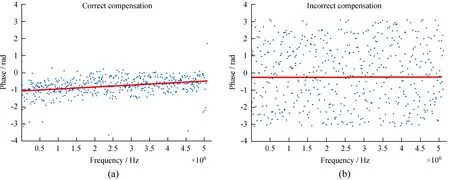
图4 在相频图上的拟合结果。(a)补偿准确的相频图拟合结果；(b)补偿不准确的相频图拟合结果

在相频图中，有一种特殊情况是相位卷绕。由(10)式可知，互相关功率谱是共轭相乘，可以得到相位是相加的关系，表示为

φ(f)=φ1(f)+φ2(f) .

(13)

已知φ1(f)，φ2(f)取值范围在(-π, π)之间，但两者相加后取值范围可能不在(-π, π)之内。由于计算机在处理相位时只能用(-π, π)表示，此时相位图被截断而发生跳变[8]，如图5(a)。从图5可以看出条纹是存在的，但相位发生了截断，出现条纹平行的现象，导致无法对相位数据进行准确的线性拟合，过大的拟合方差也影响后续的判断。

通过上面的分析可知，因为两台站信号互相关功率谱的相位超出(-π, π)而导致相位卷绕现象。为了准确表示互相关功率谱的相位，需要对相位进行解卷绕处理。解卷绕方法为规定跳变阈值，当相位跳变超过阈值时，将相位进行迁移，使截断的相位连接在一起[9]，解卷绕后的相位如图5(b)。

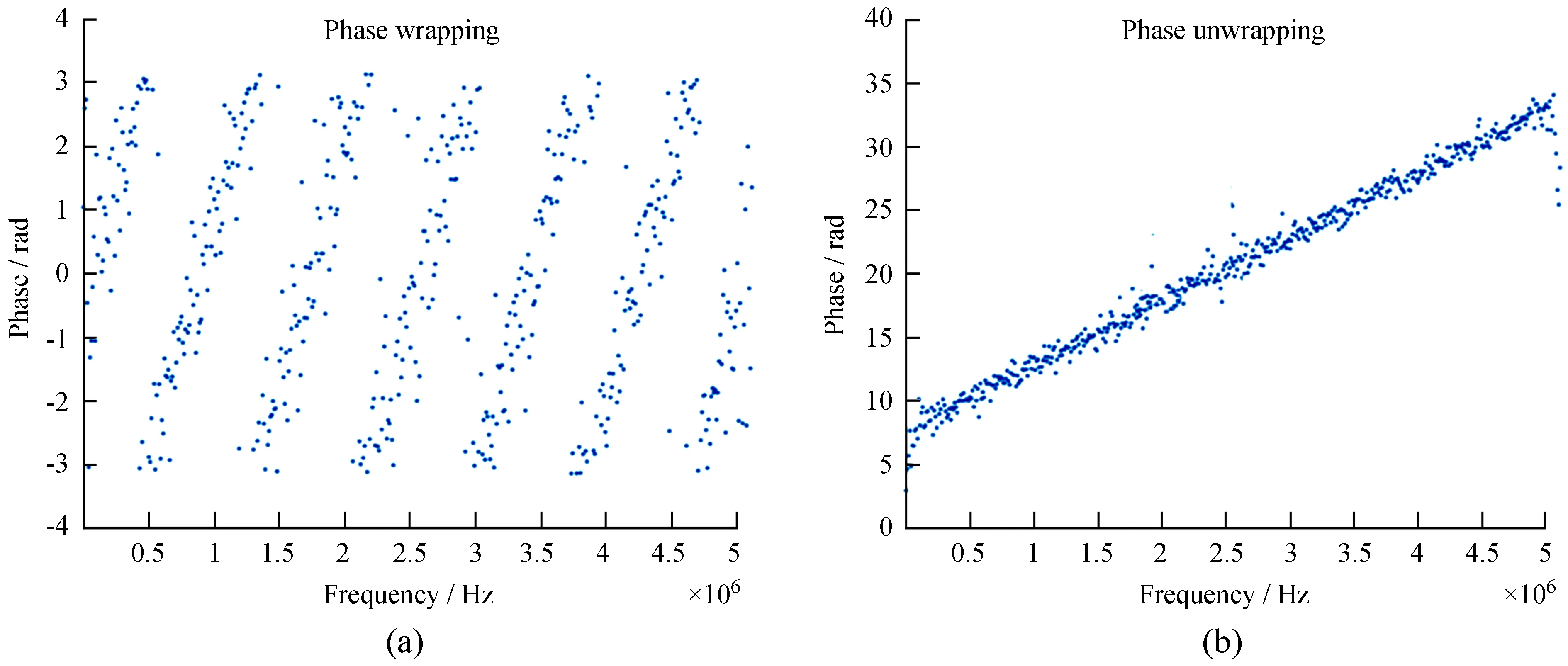
图5 卷绕与解卷绕。(a)相位卷绕；(b)相位解卷绕Fig.5 Phase wrapping and phase unwapping. (a) Phase wrapping; (a) Phase unwrapping

2.3 多重网格条纹搜索流程

图6是多重网格条纹搜索的具体流程。首先需要计算相关处理机的精度，确定粗搜索的时延和时延率补偿的搜索步长，读取台站记录的信号，解码后在绝对时间上对齐，固定台站1信号，对台站2信号进行粗搜索的滑窗处理，完成时延和时延率的补偿后计算互相关功率谱，搜索到互相关功率谱弥散程度最小的位置，缩小搜索范围，以满足精度要求的搜索步长进行相关处理，在信号相关后得到互相关功率谱，提取相位。计算每组时延、时延率对应相位的方差并记录，最后将记录的方差结果绘制输出，选取峰值对应的时延、时延率，最终得到精确的时延、时延率并输出。

3 实测信号验证

为了验证多重网格条纹搜索的正确性，我们以嫦娥四号探月工程中一段实测数据进行验证，其观测代码为s8b06a，观测源为3C 273B。采用FX型相关处理机。本次实验选择天马站和乌鲁木齐站的信号，采样率为4 MHz, 采用2 bit量化，划分为16个通道，通道带宽为2 MHz，积分时间2 s。实验选取第1通道的信号，中心频率f0为2 233.5 MHz。由(11)式和(12)式计算可知，时延、时延率补偿的精度需要满足：

(14)

(15)

算法本身对时延和时延率的搜索范围在理论上没有硬性约束，为了方便，在实验操作时，以先验模型为初值确定较大的搜索范围。在工程应用中，若有更大的搜索范围需求而带来更大的计算量，可通过信息传递接口(Message Passing Interface, MPI)、统一计算设备架构(Compute Unified Device Architecture, CUDA)等并行计算技术实现。

首先选择粗网格进行搜索，时延搜索步长为1 × 10-5s，时延率搜索步长为1 × 10-9s/s。在搜索范围内，分别计算不同的时延和时延率对应的互相关功率谱的相位方差σ2。为了使结果更加直观，取σ2的倒数Q绘制成图7(a)，得到峰值位置为补偿时延2.88 × 10-3s，补偿时延率7.15 × 10-7s/s。因此，时延补偿的范围为2.87 × 10-3～2.89 × 10-3s，时延率补偿的范围为7.14 × 10-7～7.16 × 10-7s/s，在此范围内进行更为精确的条纹搜索，得到时延、时延率补偿的精确值。

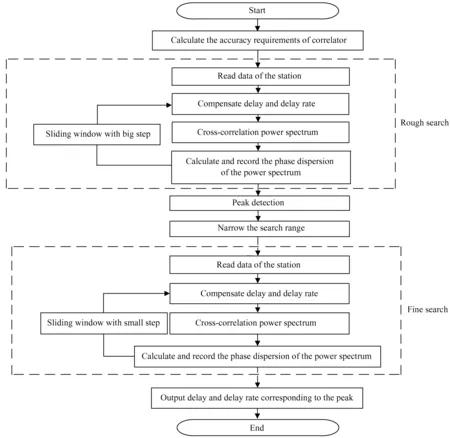
图6 多重网格条纹搜索流程图Fig.6 Multi-grid fringe search flow chart

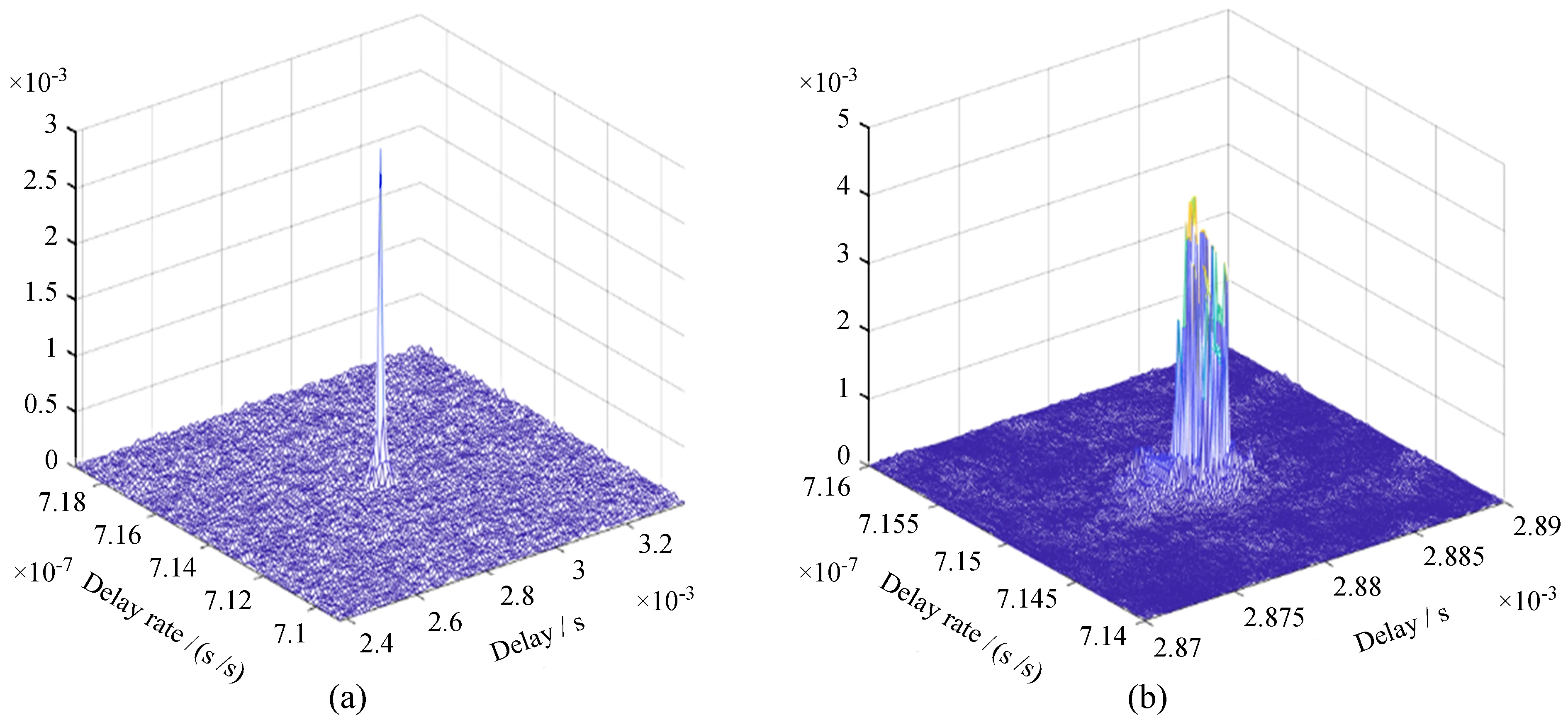
图7 多重网格条纹搜索。(a)粗网格搜索图；(b)细网格搜索图Fig.7 Multi-grid fringe search. (a) Rough grid fringe search; (b) Fine grid fringe search

经过上述操作，确定时延的精搜索范围为2.87 × 10-3～2.89 × 10-3s，时延率的精搜索范围为7.14 × 10-7～7.16 × 10-7s/s；精搜索时延步长为1 × 10-6s，时延率步长为1 × 10-10s/s。分别计算不同时延、时延率对应的Q值，绘制成图7(b)，求得峰值对应的时延为2.881 × 10-3s，时延率为7.151 × 10-7s/s。将搜索到的时延、时延率代入相关处理机进行验证，得到射电源的条纹如图8。

本文实验使用的中央处理器型号是Intel(R)Xeon(R)CPU X5650@2.67GHz。实测数据库应用中多重网格条纹搜索的窗口大小、程序运行时间等相关参数如表1。

表1 多重网格条纹搜索的相关参数Table 1 Parameters of model-free fringe searches

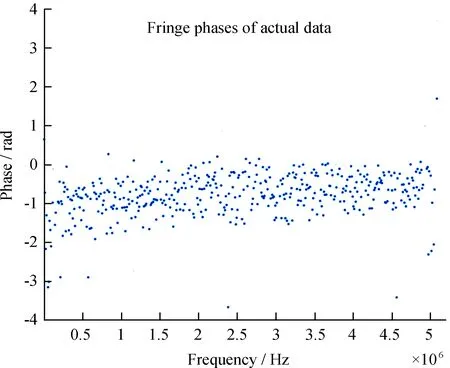
图8 实测数据条纹Fig.8 Fringe phases of actual data

4 结 论

本文针对射电源甚长基线干涉测量自动条纹搜索这一难题，基于多重网格的方法提出了一种射电源信号的条纹搜索算法，并通过嫦娥四号实测信号进行验证，该方法解决了射电源条纹搜索依赖于时延模型这一难题。基于该算法的应用背景，经过后续深入的研究，有望应用于空间甚长基线干涉测量的数据处理。