基于线性工作点的水下机器人H∞鲁棒控制

苏伟，王俊雄，王震，牛啸辰

(上海交通大学 船舶与海洋工程国家重点实验室，上海 200240)

0 引 言

水下机器人（Autonomous Underwater Vehicle,AUV）近年来在海洋工程领域发挥着越来越重要的作用，被广泛应用在水下设备安装监控、大范围海洋监测以及自然资源勘探等领域。由于水下机器人数学模型存在强耦合、强非线性、水动力学系数不确定以及不确定海流干扰等问题，为保证AUV 在复杂环境下能够正常工作，迫切需要易用且稳定性与鲁棒性良好的运动控制方法[1-6]。

AUV 的鲁棒控制方法是当前的研究热点之一，大量的工作主要集中在低自由度AUV 的线性系统控制。B.Clement 通过非线性补偿与卡尔曼滤波实现了AUV 单自由度首向角的H∞鲁棒控制结构，对比传统PID 控制具有低过冲、稳定快的优点[7]。Juan C. Cutipa-Luque 在解耦的横移-首向2DOF AUV 模型上应用H∞鲁棒控制策略，取得了较好的控制效果[8]。Wei Zhang等[9]提出插值型H∞鲁棒控制器，分别实现了速度、首向及深度控制器并给出了相应的实验结果，验证了控制器设计思路的有效性。AUV 单自由度的鲁棒控制虽然易于单个控制过程实现，但是忽略了AUV 实际上各自由度间的耦合，在实际应用上容易造成控制器设计逻辑复杂，控制环节无法有效平滑过渡以及控制器参数过多不便校准等问题。为解决AUV 多自由度系统相互耦合、强非线性等问题，本文基于六自由度AUV工作点处的线性化方程，构建适用于鲁棒控制的不确定性模型，并据此设计方便实际应用的六自由度H∞鲁棒控制器，得到了对应的仿真结果。

1 AUV 六自由度非线性模型

通过对AUV 进行刚体运动及所受外力分析，可以得到AUV 的动力学及运动学模型。为研究方便，本文采用Kambara 外形AUV 的模型进行仿真[10]。AUV 的坐标系定义如图1 所示，在此坐标系上，随体坐标系O0-X0Y0Z0到大地坐标系 O -XYZ的速度与角速度变换关系可定义为：

其中η1=[x y z]T， η2=[φ θ ψ]T， v1=[u v w]T，v2=[p q r]T。(x y z φ θ ψ)分别为大地坐标系 X0方 向位置， Y0方向位置， Z0方向位置，横滚角，纵倾角，首向角；(u v w p q r)分别为随体坐标系速度与角速度分量。J1(η2) 和J2(η2)分别为速度与角速度转换矩阵。

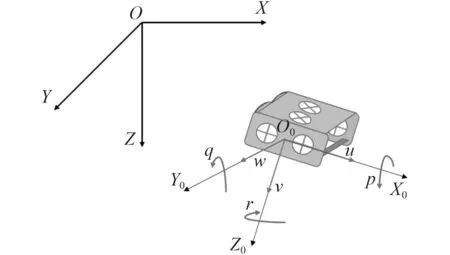
图 1 AUV 坐标系定义Fig. 1AUV coordinate system definition

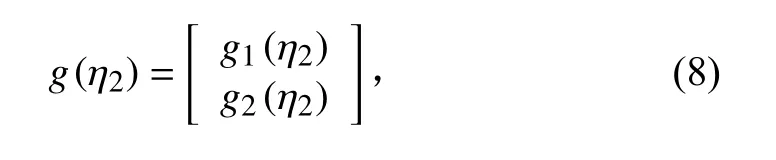
则AUV 六自由度方程可以简化为Fossen 形式[11]，且M可逆，AUV 六自由度非线性模型为：

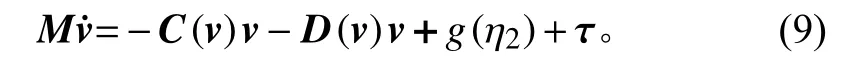
2 六自由度AUV 工作点处不确定性模型

本文所提出的六自由度AUV 不确定性模型建立在AUV 工作点处的线性化方程以及鲁棒控制中的加性不确定性模型之上，并最终在频域上对其进行描述，得到耦合性未丢失且方便处理的多自由度控制模型。

为便于处理，定义模型控制输入为τe=τ-g(η2)，并且式（9）中C(v)， D(v)分别具有如下形式的非线性项：

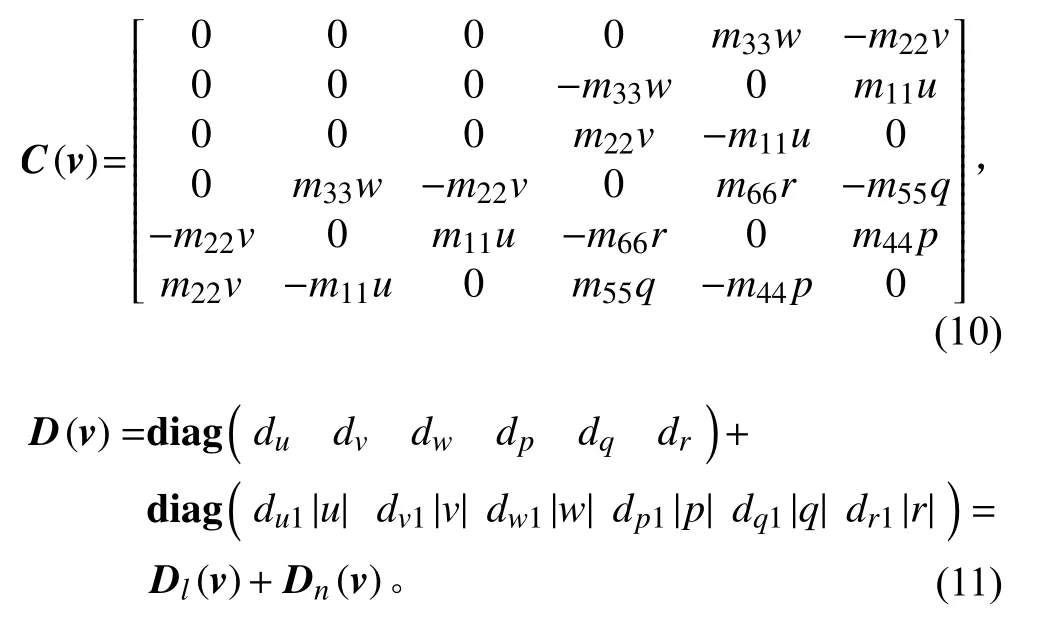
式中： mii， dj均为模型常数。对于D(v)中的非线性阻尼项Dn(v)，考虑到AUV 最大速度小于 0 .8 m/s，最大转动角速度小于0.5 rad/s，通过最大速度界函数Dn(vmax)近似非线性阻尼项使其满足范数意义下‖Dn(vmax)‖≥‖Dn(v)‖。

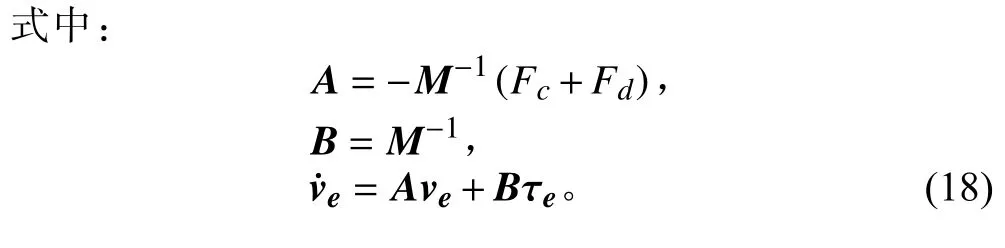
将非线性阻尼项 Kd视为模型不确定性因素，不确定性系统 G0可表示为：

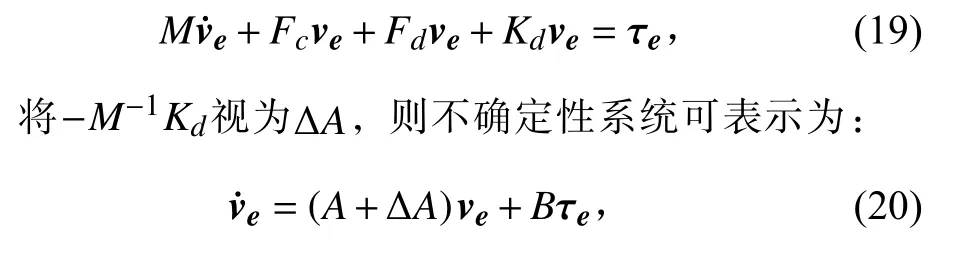
将不确定性因素考虑为加性不确定性，则不确定性系统 G0与 标称系统G 满足如下关系：

其中Wd(s) 为 描述系统不确定性的界函数， Δ (s)为系统未知摄动。系统加性摄动模型如图2 所示。

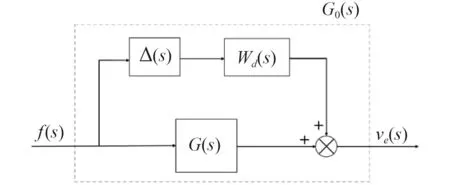
图 2 AUV 加性摄动模型Fig. 2AUV additive perturbation model

由于本系统为六自由度高阶系统，保持结果准确并且降低系统模型复杂性，可通过传递函数差值的频率响应得到满足要求的2 阶加性摄动界函数Wd(s)，使得该界函数满足：

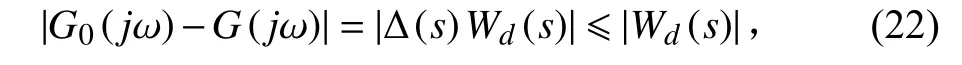
根据文献[10]中的六自由度非线性AUV 模型，可得到在工作点 v0处展开的系统参数如下：

为不失一般性，在v0=(0.4 0.4 0.4 0.25 0.25 0.25)工作点处展开，通过式（22）可求得加性摄动界函数Wd(s)。不确定系统在 v0处的奇异值如图3 所示。

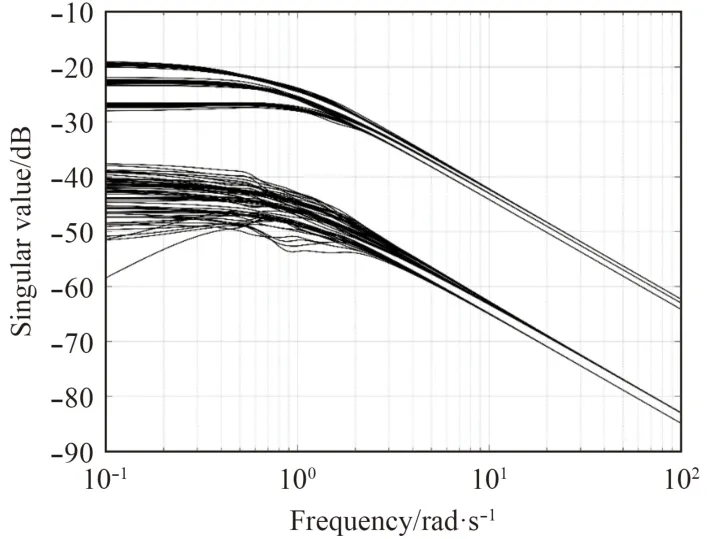
图 3 六自由度AUV 不确定性系统奇异值Fig. 3Singular values of the six-DOF AUV uncertainty system

3 AUV 线性模型的H∞控制器

本文采用回路成形设计方法得到六自由度AUV 不确定性模型H∞控制器，设计时采用经典的闭环控制结构如图4 所示。其中r 为参考输入，d 与n 分别是输出扰动与传感器噪声，y 为系统输出。

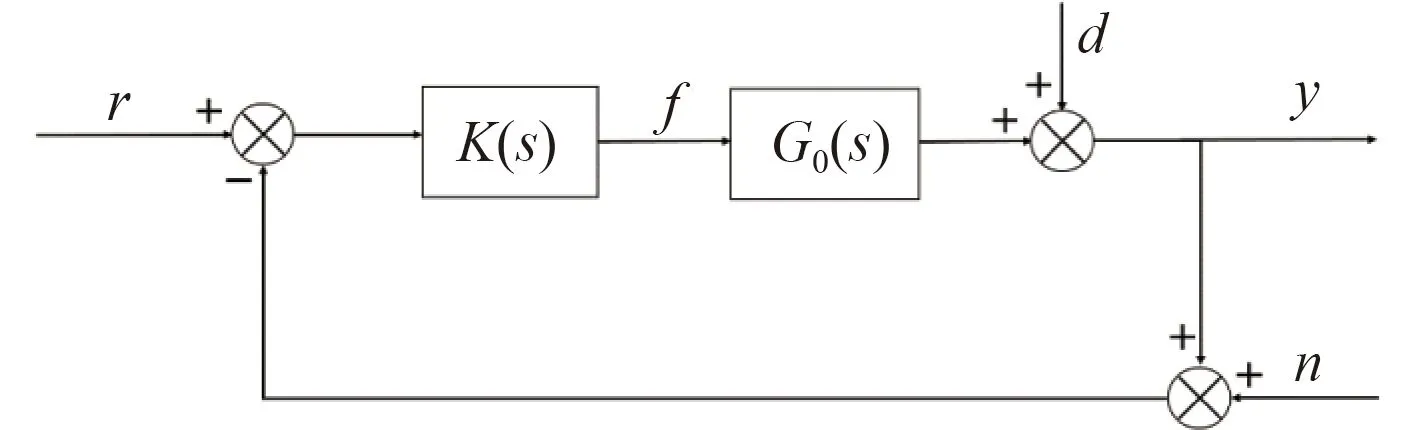
图 4 闭环控制结构图Fig. 4The closed-loop control structure

开环传递传递函数L(s)=G0(s)K(s)，定义敏感函数S(s)=(I+L(s))-1及补敏感函数T(s)=L(s)(I+L(s))-1。敏感函数与补敏感函数满足S(s)+T(s)=I，则闭环输入输出结构中的传递函数关系满足：

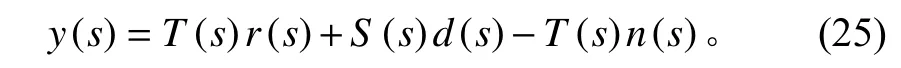
得到的控制器K(s)在满足将系统G0(s)镇定的同时，根据公式：

1）在低频段范围使 | L(jω)|＞＞1，以保证控制器对低频干扰不敏感且具有良好信号跟踪能力；

2）在高频段范围使 | L(jω)|＜＜1，以保证控制器有良好的高频噪声抑制能力。

满足条件的控制器由如下定理[13]确定：

定理设 G 与 K分别为控制对象与控制器， ζ为全体稳定实有理传递函数集合，G(s)G 在 ζ中的一个互质分解。X,Y ∈ζ，满足XN+YM=1，则使闭环系统内稳定的所有控制器 K的集合为：

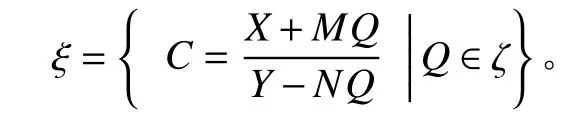
其中 Q 为控制器参数。

本文计算得到的控制器用于在v0=(0.4 0.4 0.4 0.25 0.25 0.25)工作点的六自由度AUV 系统，该控制器在回路成形计算时选取了Gd=100/s作为目标曲线进行成形计算，得到控制器K(s)的奇异值如图5 所示。该六自由度控制器在低频段具有更大的控制作用以增强系统的跟踪性能。该控制器求解得到的开环传递函数L(s)的结果如图6 所示，可以看出该曲线很好满足了开环传递函数目标曲线。在低频段开环传递函数的奇异值远大于1，在频率大于100 rad/s后开环传递函数奇异值开始快速减小以提高对高频干扰噪声的抑制能力。

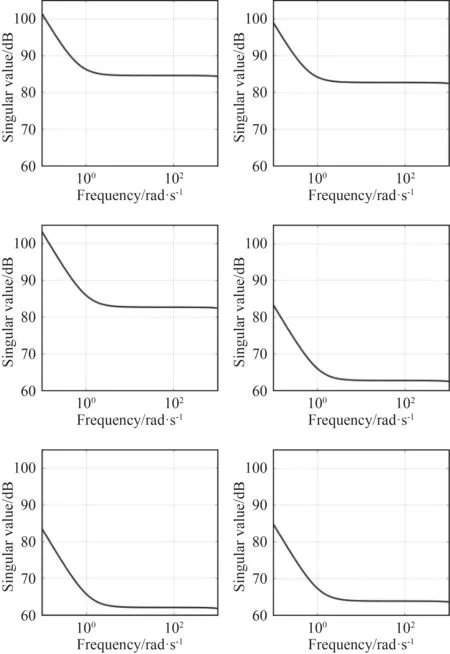
图 5 给定工作点处六自由度鲁棒控制器奇异值曲线Fig. 5The singular value curve of the 6-DOF robust controller at a given operating point

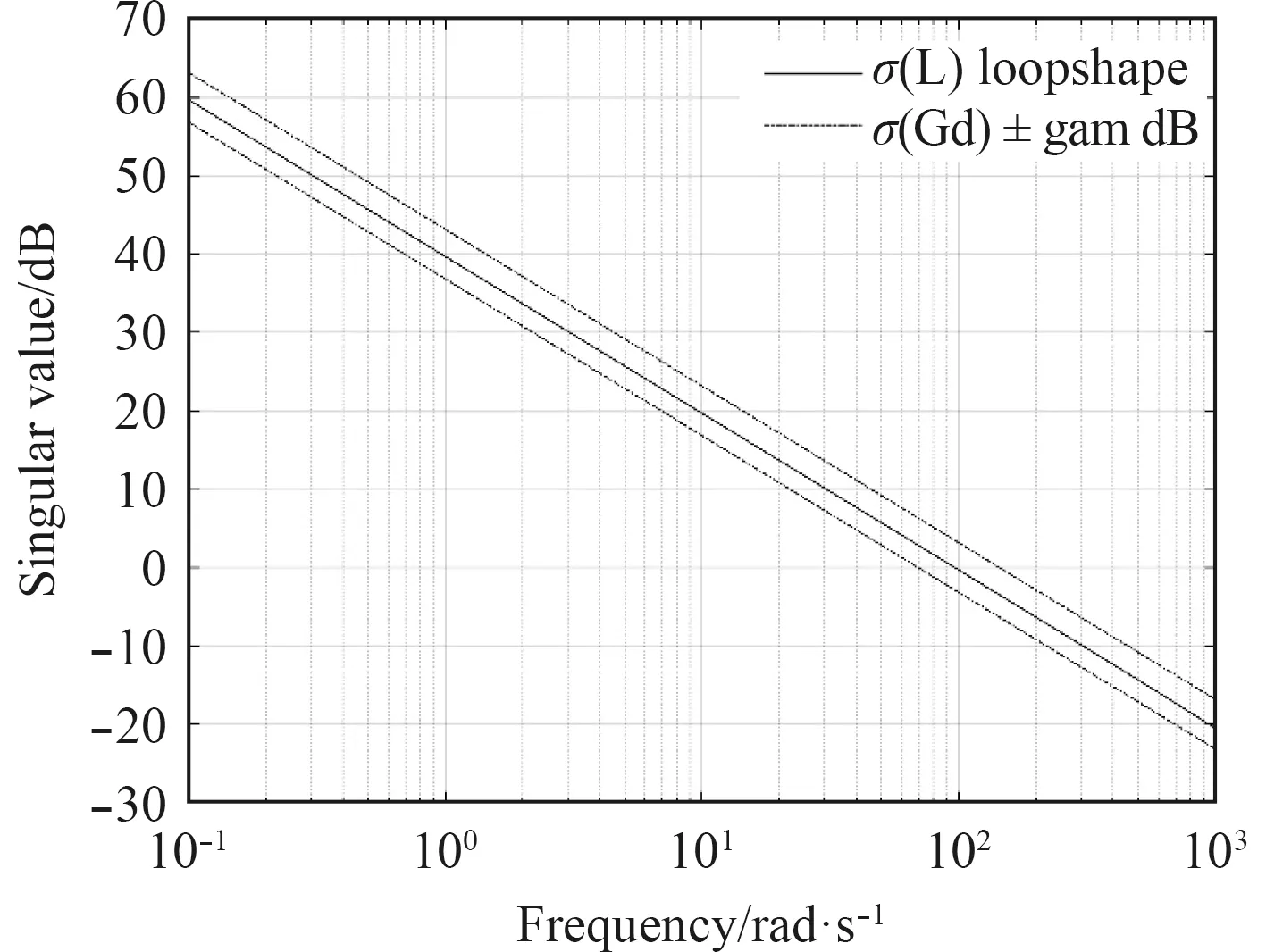
图 6 开环传递函数奇异值曲线Fig. 6Singular value curve of the open-loop transfer function

4 H∞控制器仿真结果

将控制器作用于给定工作点 v0后的六自由度AUV系统，图7 与图8 分别给出了作用控制器后闭环系统的敏感函数曲线以及补敏感函数曲线。得到的闭环系统敏感函数在高频奇异值减小，体现了鲁棒控制器在高频对干扰信号的抑制能力已经得到保证。补敏感函数曲线中低频段曲线集中在分贝值0 dB 附近，表示系统在低频段具有良好的参考信号跟踪能力。而且，低频段的补敏感函数频带较宽，表示控制器具有较好的性能鲁棒性。

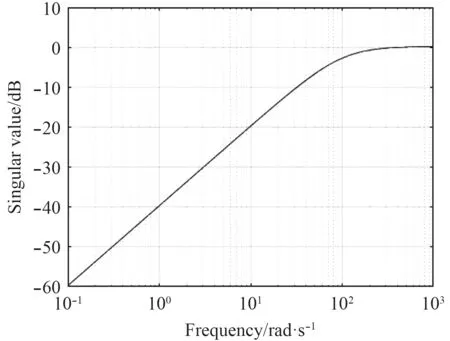
图 7 闭环系统的敏感函数曲线Fig. 7Sensitivity function curve of the closed-loop system

图9～图11 给出了闭环系统在工作点 v0时，在u 方向输入0.15 m/s 正弦信号，w 方向输入-0.15 m/s，同时在u，v，w 方向均施加频率为30 rad/s，幅值为0.015 m/s 的正弦干扰信号，其余参考信号均为0 的情况下鲁棒控制器与PID 控制器六自由度响应对比曲线。从图中可以看出，鲁棒控制器在更短的时间内满足了阶跃信号的输入要求，并在10%幅值的正弦扰动下仍旧能够保持稳定性，表示该鲁棒控制器具有良好的信号跟踪能力。通过干扰抑制的数据对比，鲁棒控制器相比PID 控制器对高频干扰有更强的抑制能力。同时，由于本系统为耦合系统，从图中可以看出非参考信号的自由度之间耦合影响不大，说明该鲁棒控制器具有优良的抗干扰能力。

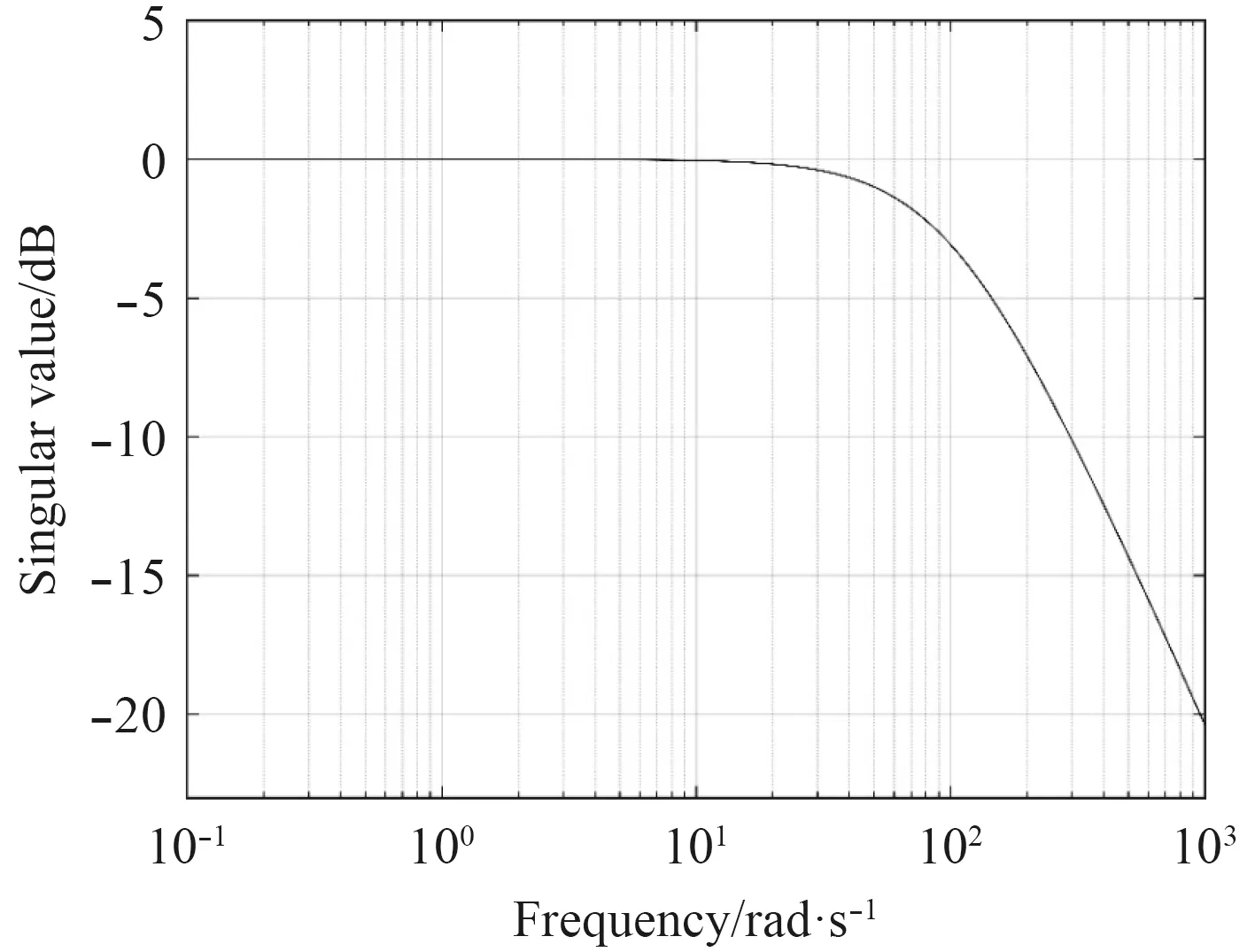
图 8 闭环系统的补敏感函数曲线Fig. 8Complementary sensitivity function curve of the closed-loop system

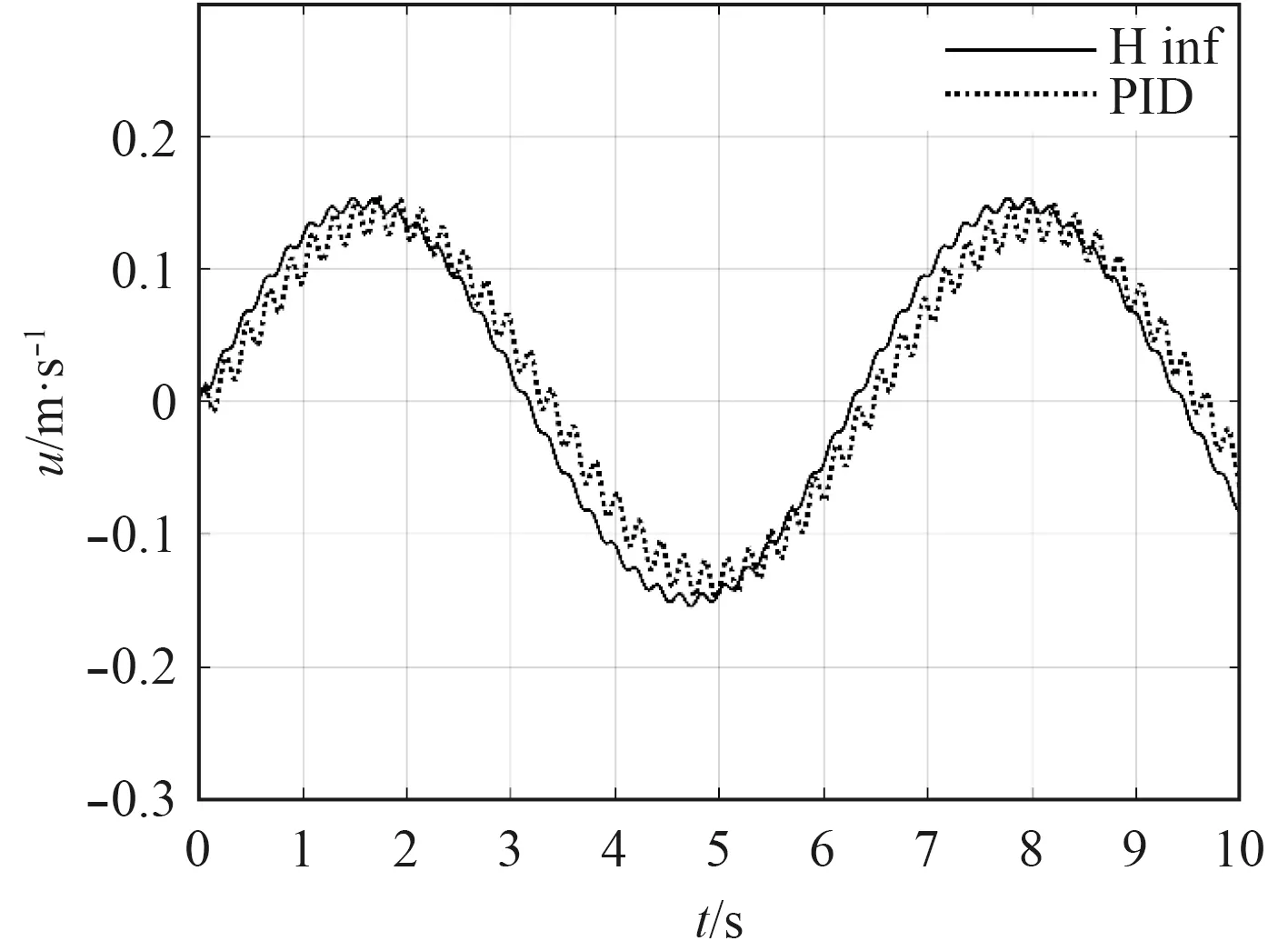
图 9 u 方向对比响应曲线Fig. 9Response curve in u direction

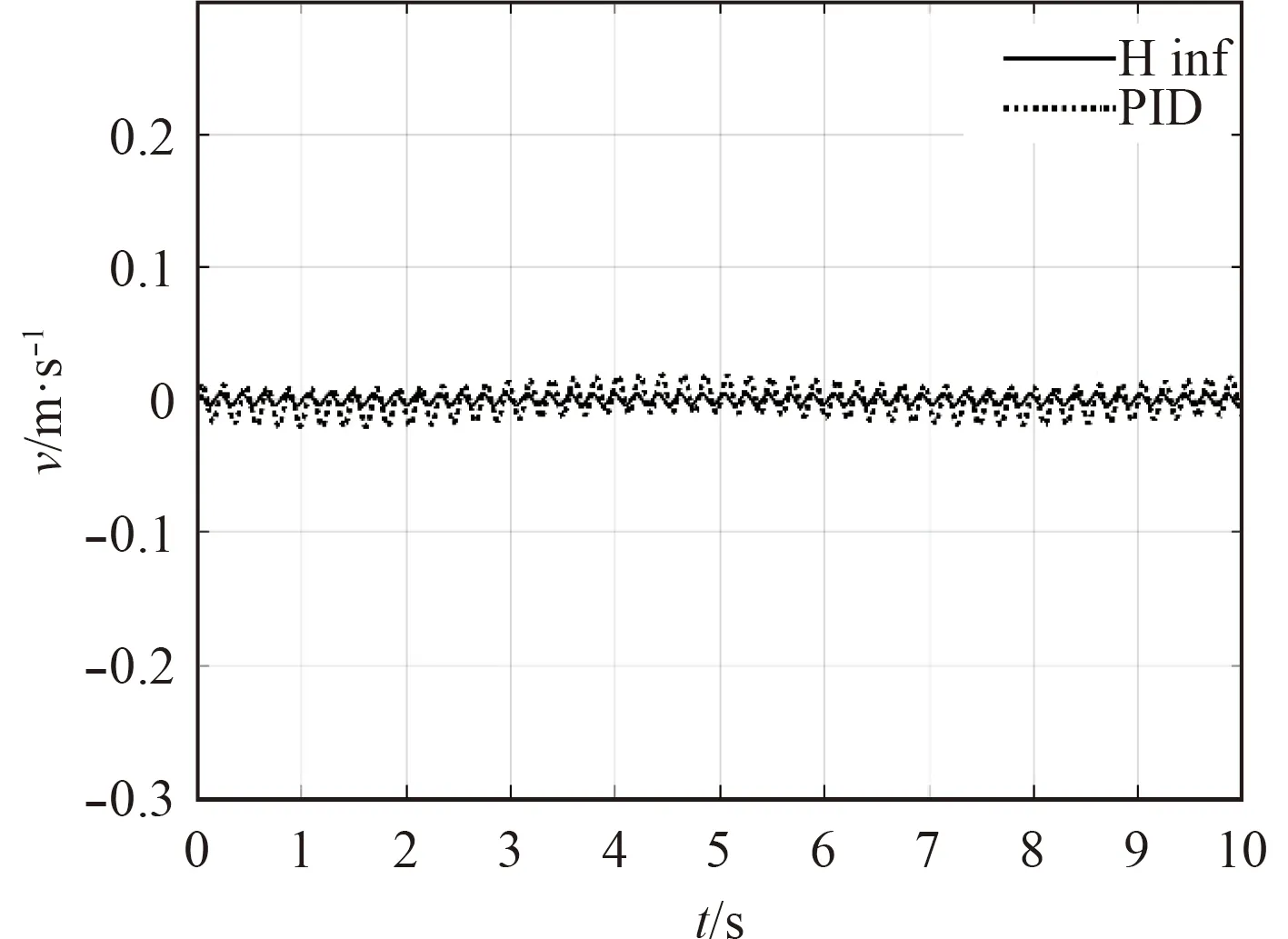
图 10 v 方向对比响应响应曲线Fig. 10Response curve in v direction

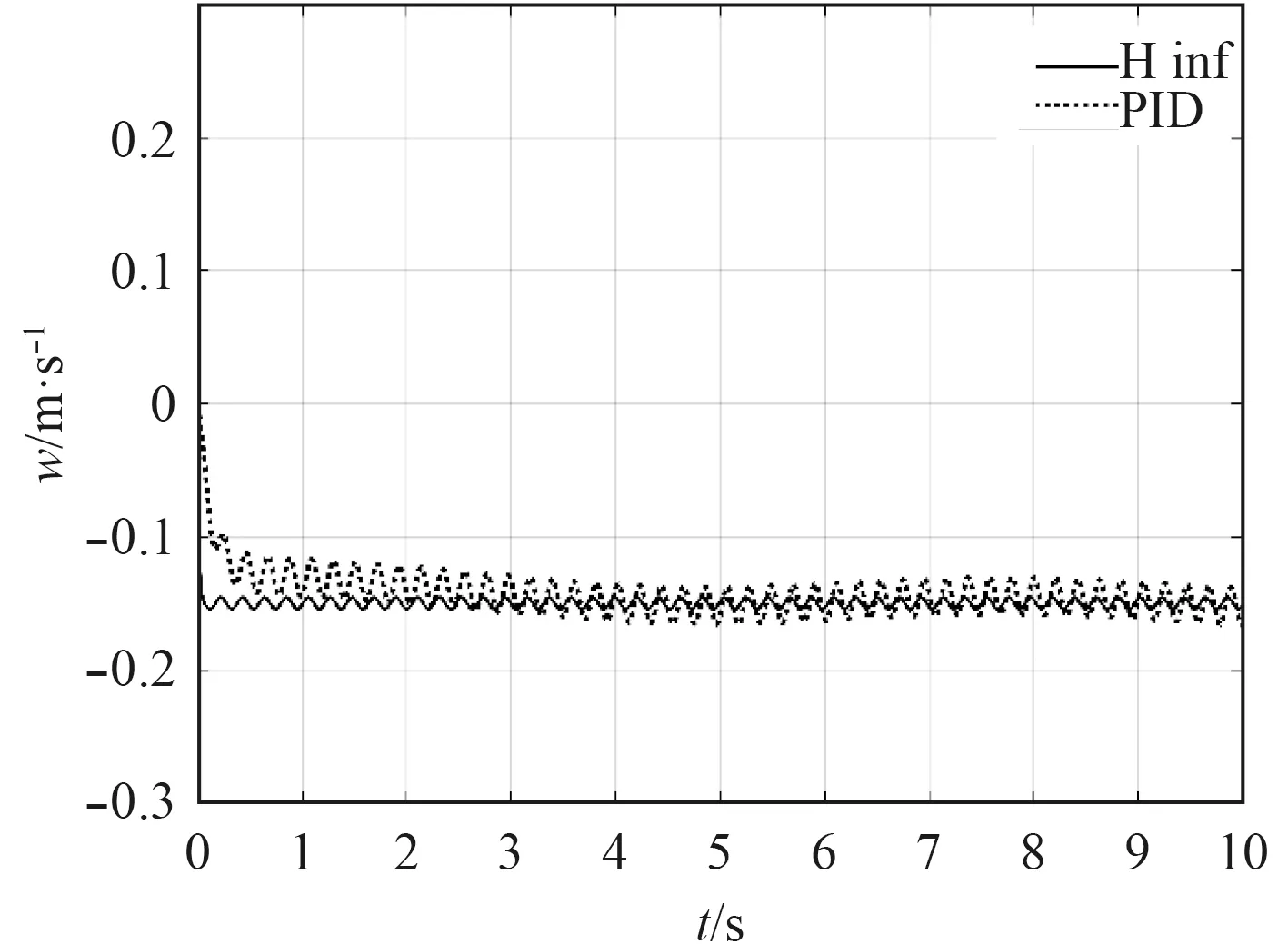
图 11 w 方向对比响应响应曲线Fig. 11Response curve in w direction

5 结 语

本文通过对自由度间相互耦合、强非线性的AUV模型在工作点附近进行了线性化，给出了该线性化模型的操作过程及结果，并据此建立了适合应用鲁棒控制方法的加性不确定性模型。使用回路成形方法得到了对应工作点的鲁棒控制器，对闭环系统的仿真试验取得了良好的控制效果，验证了回路成形方法设计的鲁棒控制器在多自由度AUV 系统中使用的有效性，未来可以针对多个工作点的鲁棒控制器连续工作做进一步的研究。