参数优化变分模态分解与多域流形学习的行星齿轮箱故障诊断

王振亚， 姚立纲， 戚晓利， 张 俊， 郑近德

(1. 福州大学 机械工程及自动化学院， 福州 350116； 2. 安徽工业大学 机械工程学院， 马鞍山 243032)

行星齿轮箱作为旋转机械的关键部件，在直升机主减速器、风力发电机组等复杂传动系统都有着较广泛的应用[1]。但在实际运行过程中，由于行星齿轮箱振动信号易受噪声污染与振动复杂等影响，增加了对其进行故障诊断的难度[2]。

目前，常见的故障信号降噪方法主要包括：小波变换，经验模态分解(Empirical Mode Decomposition，EMD)和局部均值分解等。如徐金梧等[3]利用小波变换提取出被噪声所掩盖滚动轴承故障冲击成分；杨宇等[4]将EMD应用于故障信号预处理过程；程军圣等[5]提出一种基于局部均值分解与能量谱相结合的齿轮故障诊断方法，并均取得良好实验效果。然而小波变换事先需要选择小波基和分解层数等，缺乏自适应性；EMD存在频率混淆、过包络、欠包络、端点效应等局限[6]；局部均值分解具有运算速度慢、信号冲突问题等缺陷[7]。变分模态分解(Variational Mode Decomposition, VMD)[8]是在传统维纳滤波基础上，研发的一种非递归自适应信号分解新方法，与小波变换、EMD和局部均值分解等方法相比，VMD分解的信号，具有精度高、收敛快和鲁棒性好等特点，非常适用于处理行星齿轮箱故障信号。但VMD算法信号处理效果与惩罚因子和分解个数这两个参数密切相关，为了能够有效从噪声干扰下提取行星齿轮箱故障信号分量，实现最佳信号处理效果，本文将寻优能力强的新型元启发式算法——樽海鞘群算法(Salp Swarm Algorithm, SSA)[9]应用于VMD的参数寻优过程，提出了樽海鞘群优化变分模态分解(Salp Swarm Optimization Variational Mode Decomposition, SSO-VMD)，并将其应用于行星齿轮箱信号预处理过程。

行星齿轮箱故障诊断的关键在于特征提取，为全面表征故障信息，从时域、频域和尺度域提取特征参数，构造成原始多域故障特征集。由于该故障集具有非线性、高维、冗余等特性，直接输入至分类器中进行模式识别，可能影响识别效果。流形学习能够有效挖掘出非线性数据集嵌入在高维空间中的低维流形成分，为实现高维故障特征集维数约简提供更为理想的解决途径。经典的流形学习算法主要包括：等度规映射(Isometric Mapping, Isomap)[10]、局部切空间排列[11]、界标点等度规映射(Landmark Isomap, L-Isomap)[12]、t-分布邻域嵌入(t-Distributed Stochastic Neighbor Embedding, t-SNE)[13]等算法。但上述方法均为无监督降维方法，降维过程没有利用样本标签信息，不太适合存在诸多奇异数据点的行星齿轮箱特征降维过程[14]。因此，本文引入一种改进监督型自组织增量学习神经网络界标点等度规映射(Improved Supervised Self-organized Incremental Learning Neural Network Landmark Isomap, ISSL-Isomap)[15]流形学习新算法，将其应用于多域故障特征集维数约简过程，以获取低维、敏感的故障特征向量。

行星齿轮箱故障诊断的本质在于模式识别，利用新型机器学习算法——人工蜂群优化支持向量机(Artificial Bee Colony Support Vector Machine, ABC- SVM)[16]对“SSO-VMD+多域故障特征+ISSL-Isomap流形学习”低维特征进行诊断识别。行星齿轮箱故障诊断实验分析结果表明所提方法能够精准、有效识别出各故障类型。

1 参数优化变分模态分解

1.1 变分模态分解算法

VMD是一种新的自适应信号分解方法，该方法通过循环迭代来搜寻变分模型的最优解，确定本征模态分量(Intrinsic Mode Functions, IMF)的频率中心及带宽，实现各分量的有效分离。VMD算法的约束变分模型如下

(1)

式中：K表示IMF分量总数；{uk}={u1,u2,…,uK}与{ωk}={ω1,ω2,…,ωK}分别表示K个IMF分量及其对应的中心频率

将二次惩罚因子α和拉格朗日乘法算子λ(t)引入上式，得到增广拉格朗日函数

(2)

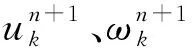
(3)

唐贵基等详细给出了VMD完整算法，并验证该算法优于现有的模态分解模型。但VMD性能易受惩罚因子α和IMF分量个数K的影响：当惩罚因子α选取不当时，VMD将无法获得最佳带宽的IMF分量；当分量个数K设置不合理时，则会出现过分解或欠分解现象。因此，选取合适的受惩罚因子α和IMF分量个数K成为目前需要解决的关键问题。

1.2 樽海鞘群优化变分模态分解算法

樽海鞘群算法利用“链”结构模式有效避免传统“群”结构模式(如粒子群，蚁群，灰狼群等)中因领导者前期搜索不充分而陷入局部极值情况的发生，并且该算法能够有效寻找全局最优解。因此，本文采用樽海鞘群算法对VMD参数进行优化选取，其中如何确定合适的适应度函数成为优化过程的要点。对于VMD分解后的IMF分量，若该分量包含较多的故障特征信息，其波形会出现规律性脉冲，同时呈现出较强的稀疏特性，因此包络熵值较小；反之，若该分量包含较多噪声信息，其波形的规律性脉冲不明显，信号的稀疏特性较弱，故包络熵值较大。本文将樽海鞘所处空间位置(对应参数α和K)下，利用VMD分解后全部IMF分量的包络熵均值定义为适应度值，并以最小包络均熵为寻优目标，实现VMD的参数寻优过程。

樽海鞘群优化变分模态分解(SSO-VMD)流程如图1所示，具体步骤如下。

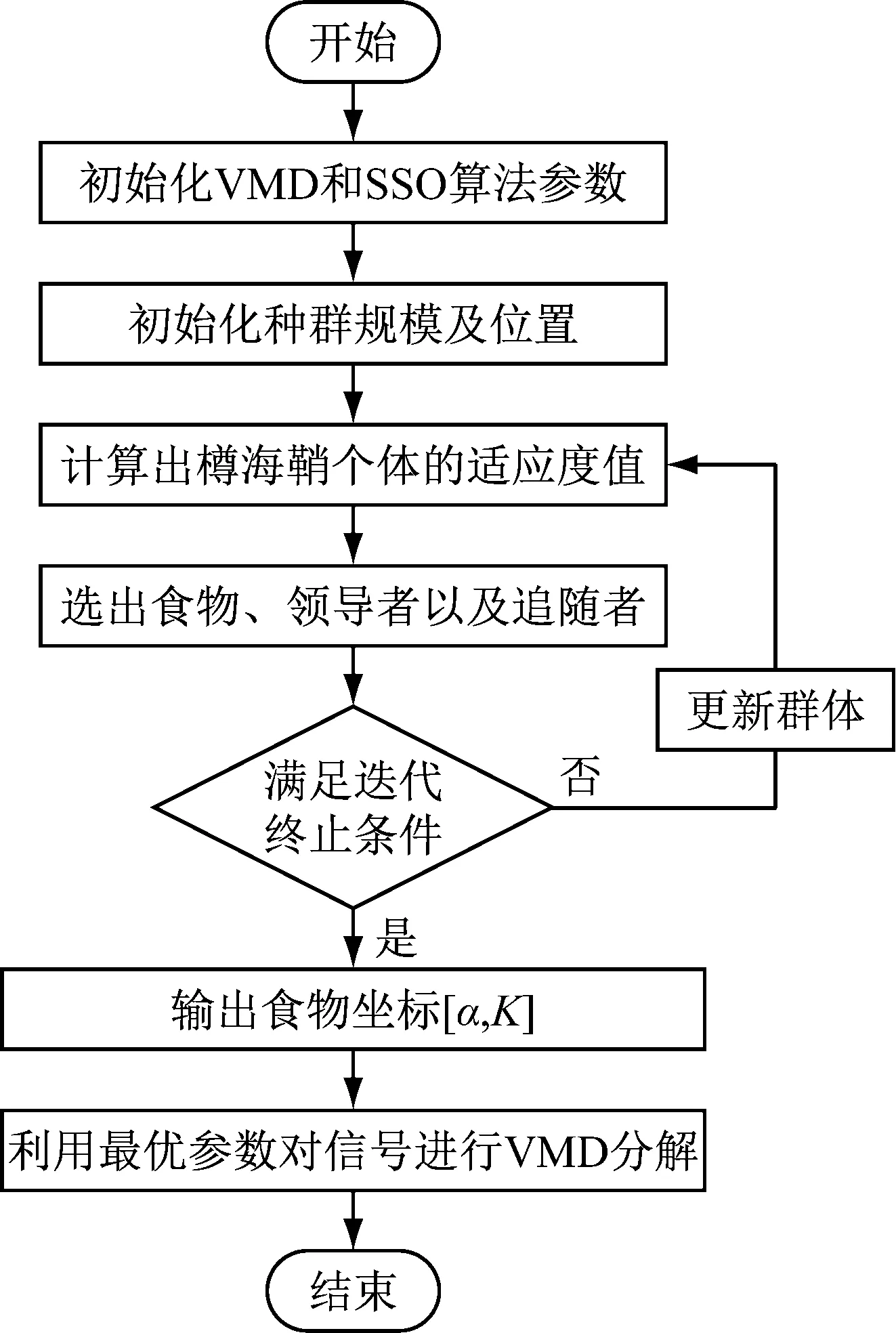
图1 SSO-VMD流程

步骤1初始化樽海鞘群优化算法的各项参数以及寻优参数寻优过程中的适应度函数。

步骤2樽海鞘群优化算法中若迭代次数较少，则会因前期搜索不充分，导致无法获取全局最优解；反之迭代次数过大，会增加寻优时间，影响算法的效率。此外，樽海鞘群优化算法的种群规模通常设置为10～50之间。因此，针对VMD参数寻优，本文初始化樽海鞘种群规模为15，设定最大迭代次数为30，将参数组合[α,K]定义为樽海鞘个体的位置，随机产生与种群规模相对应的参数组合作为樽海鞘个体的位置。

步骤3计算每个樽海鞘当前位置下对应的适应度值。

步骤4将樽海鞘个体按照适应度值大小进行升序，令排在首位樽海鞘为领导者，剩余为追随者，并将适应度值最小的樽海鞘个体所处的空间位置定义为当前食物位置。

步骤5按照式(4)更新领导者所处空间位置

(4)

c1=2e-(4l/lmax)2

(5)

式中:l为当前迭代次数;lmax为最大迭代次数。

按照式(6)更新追随者所处空间位置

(6)

步骤6计算更新后樽海鞘个体的适应度值，并与当前食物的适应度值进行比较，若更新后的樽海鞘适应度值优于食物，则将该樽海鞘的位置定义为新食物位置。

步骤7重复步骤5～步骤6，直到满足迭代终止条件，输出食物坐标，即为最佳α和K参数值。

1.3 仿真实验

为验证SSO-VMD算法的有效性，将其应用于仿真信号的分解过程，仿真信号表达式如下

x(t)=x1(t)+x2(t)+x3(t)+x4(t)

x1(t)=sin(40πt);x2(t)=sin(90πt);

x3(t)=sin(180πt);x4(t)=sin(300πt)

(7)

其中，采样频率为3 000，采样点为1 200，仿真信号及各分量时域波形如图2所示。

为了对比，本文利用EMD和SSO-VMD对该信号进行分解，分解结果分别如图3和图4所示，其中SSO-VMD的寻优结果为[295, 4]，全局最佳适应度值为0.618 2。据图3可知，EMD分解得到5个IMF分量和一个残量，出现过分解和模态混叠现象，且第1个IMF分量失真严重。据图4可知，SSO-VMD可以有效将各分量分离，分解结果与原信号分量一致，拥有较好保真度，对比验证了SSO-VMD算法的优越性。

此外，为验证樽海鞘群算法进行VMD参数寻优的有效性，利用交叉验证法(Δα=100,ΔK=1)计算不同参数组合下的包络熵均值，结果如图5所示。由图5可知，当参数组合为[300, 4]时，得到全局最小包络熵均值(数值为0.620 4)，这与樽海鞘群算法寻有结果(寻优参数为[295, 4])较为接近，以此验证将樽海鞘群算法应用于VMD参数寻优是切实可行的。

图2 仿真信号时域波形

图3 EMD分解结果

2 多域高维特征提取及流形学习

2.1 多域高维特征提取

为全面挖掘出能反映行星齿轮箱不同工况下的特征信息，本文提取振动信号16个时域特征值，13个频域特征参数和20个尺度域特征参数，各特征值表达式如表1所示，其中，TF1～TF16为时域特征参数，FF1～FF13为频域特征参数，CF1～CF20为尺度域特征参数。然后对各域特征值分别进行归一化处理，合并成多域高维故障特征。

图4 SSO-VMD分解结果

显然，所得多域故障特征集具有高维、非线性、冗余等特性，对数据的后续处理带来一定困难。为进一步提取低维、敏感故障特征，本文将流形学习算法引入至该高维故障特征集的维数约简过程。

图5 交叉寻优结果

2.2 改进监督型自适应自组织增量学习神经网络界标点等度规映射算法

界标点等度规映射(L-Isomap)算法是一种经典流形学习算法，能够有效挖掘出嵌入在高维空间的低维流形，但该算法存在以下3点缺陷：① 界标点选取问题，当界标点选取不当，会导致降维效果大大折扣；②该方法为无监督降维算法，未充分利用面向分类的类判别特征，不太适合行星齿轮箱故障信号这类存在诸多奇异数据点的情况；③ L-Isomap仅考虑样本点之间的欧式距离，但欧氏距离只能反映样本点之间的空间位置关系，不能反映流形结构关系。针对上述问题，文献[15]提出一种改进监督型自组织增量学习神经网络界标点等度规映射算法(ISSL-Isomap)，有效克服以上3点不足，并通过仿真实验验证该方法的优越性，因此本文将其应用于多域故障特征维数约简过程。对于高维空间样本集X={x1,…,xi,…,xN}，xi∈RD，ISSL-Isomap算法的具体步骤如下：

表1 多域特征参数

步骤1利用自组织增量学习神经网络算法确定界标点集合L={xl1,xl2,…,xln}；

步骤2采用余弦相似度与欧氏距离相结合的距离度量方式，构建改进距离矩阵D={dij(xi,xj)}：

(8)

步骤3构建监督型成对约束邻域图GML(V,E)和GLL(V,E)；

步骤4建立监督型距离矩阵Ds={ds(xi,xj)}，表达式下

(9)

步骤5利用Dijkstra方法寻找最短路径，构造近似测地距离矩阵xG={dG(xli,xj)}n×N；

步骤6运用多维标度分析(Multidimensional Scaling, MDS)算法对界标点进行低维映射，得到界标点低维坐标YL；

步骤7应用界标点多维标度分析(Landmark MDS, LMDS)算法计算非界标点数据的低维坐标YN-L。

3 行星齿轮箱故障诊断实验分析

3.1 故障诊断模型

提出一种基于参数优化变分模态分解和多域流形学习的行星齿轮箱故障诊断方法，流程如图6所示，具体步骤如下：

步骤1信号采集：在一定采样频率fs下，分别采集Q种工况下行星齿轮箱故障振动加速度信号q组，共计Q×q组信号；

步骤2信号降噪：利用樽海鞘群优化变分模态分解算法(SSO-VMD)对各组加速度振动信号进行分解，并将所得若干IMF分量进行重构；

步骤3多域故障特征构建：对重构信号进行多域特征参数提取，Q×q组样本即可得到高维故障特征集F(Q×q)×49；

步骤5模式识别：每种工况随机挑选p组样本的低维故障特征作为训练样本，用于构建人工蜂群优化支持向量机(ABC-SVM)多故障预测模型(采用一对一的方式)，剩余q-p组样本的低维故障特征作为测试样本，输入至预测模型中进行诊断识别，确定故障类型。

图6 故障诊断模型

3.2 故障诊断实验分析

为验证本文所提方法的有效性，在行星齿轮箱实验台上进行了太阳轮正常状态，磨损状态，裂纹状态和断齿状态等4种工况的瞬态实验。实验平台及故障分布如图7所示。本次实验设置电机转速为600 r/min，采样频率为fs=10 240 Hz，利用1号传感器进行样本信号的采集，按照时间顺序以2 048个采样点为一组样本，每种工况各采集100组样本，四种工况共计400组样本，不同工况下的振动加速度信号时域波形如图8所示。

图7 实验平台及故障分布

由图8可知，仅从信号时域波形无法有效区分出各工况类型，并且实验采集的信号存在一定噪声干扰，因此根据故障诊断模型步骤2所示，利用SSO-VMD对上述信号进行分解与重构。以一组断齿信号为例，利用SSO-VMD算法对其进行降噪，其中，SSO算法对VMD参数寻优结果为[708, 3]，全局最佳适应度值为2.687 0，并对上述各IMF分量进行重构，即可得到降噪后的故障信号，对应分解与重构结果如图9所示。

图8 4种工况振动加速度信号时域波形

图9 SSO-VMD对断齿信号分解与重构结果

为全面表征不同工况故障信息，对上述4种工况各100组样本分别从时域、频域和尺度域等方面进行多域高维故障特征提取，400组样本即可得到49维数特征矩阵F400×49，4种工况均值特征曲线如图10所示。为量化多域特征提取效果，将时域特征提取结果、频域特征提取结果、尺度域特征提取结果和多域特征提取结果分别输入至ABC-SVM多故障分类器中进行模式识别，其中每类工况训练样本与测试样本按4∶6随机分配，定义训练样本3折交叉后的平均识别率为适应度值，设置蜂群规模为20，终止迭代为100，蜜源数为10，控制参数为100，4种特征提取效果如表2所示。据表2可知，多域特征提取具有最高平均识别精度(达到69.58%)，提取效果明显效果优于时域、频域、尺度域等单域特征提取效果(平均识别精度分别为56.25%, 47.50%, 58.75%)。但因多域特征提取存在信息冗余，因此需要利用降维方法进行敏感、低维故障特征的二次提取。

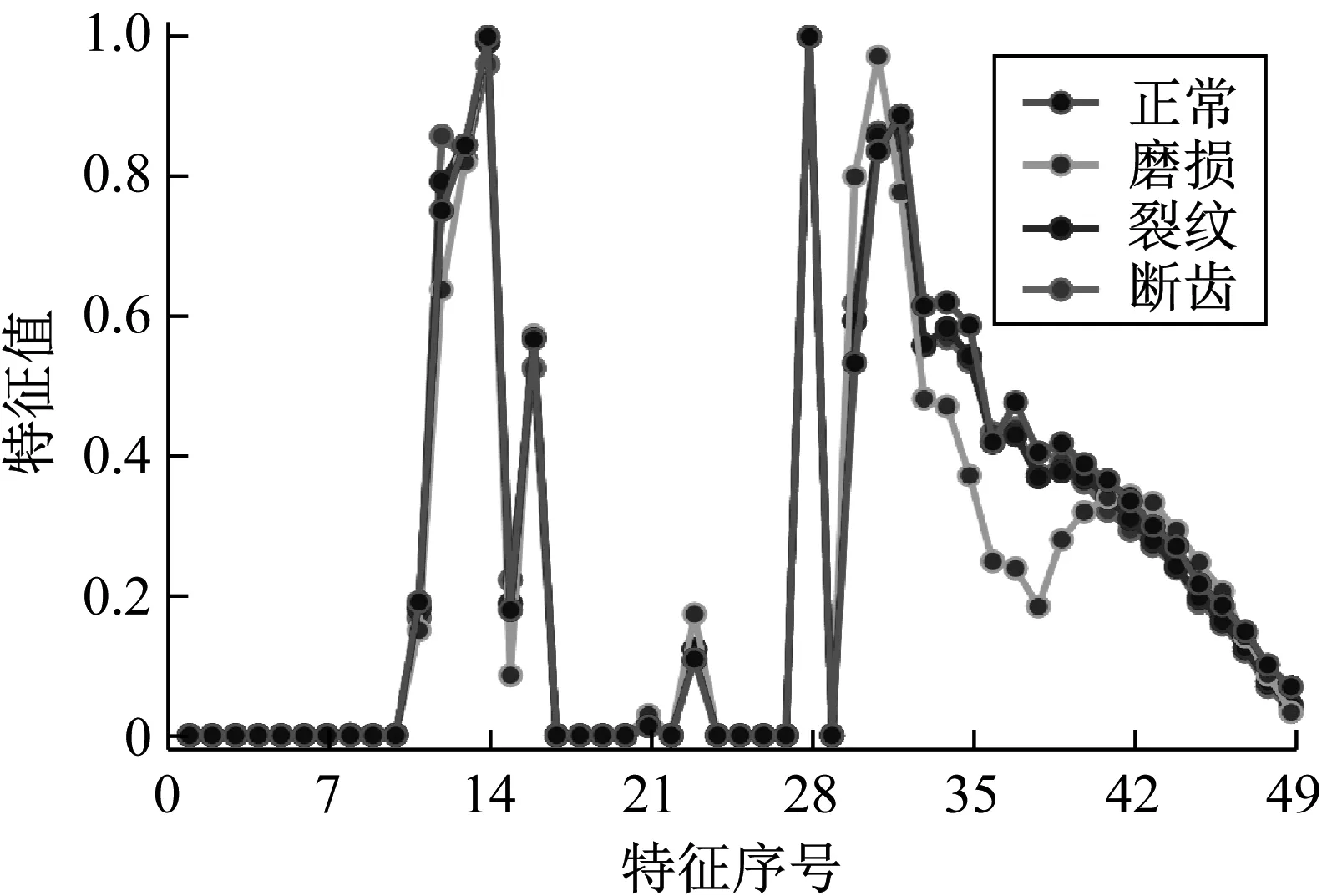
图10 4种工况均值特征曲线

利用ISSL-Isomap流形学习算法对多域故障特征集进行维数约简，为验证该算法优越性，将其与Isomap、t-分布邻域嵌入算法(t-SNE)、线性判别分析(Linear Discriminant Analysis, LDA)[17]、加权Isomap (Weighted Isomap, W-Isomap)[18]和监督Isomap(Super-vised Isomap, S-Isomap)[19]等无监督、监督降维方法进行对比。其中，利用最大似然估计法确定本征维数为5，通过多次实验确定各算法最佳参数，分别设置如下：Isomap近邻参数设置为63；W-Isomap近邻参数设置为45，权重因子设置为0.45；S-Isomap近邻参数设置为74，参数α设置为0.38；ISSL-Isomap近邻参数设置为66，调节因子1为平均改进距离，调节因子2设置为0.4，6种方法前三维可视化结果如图11所示。据图11可知，Isomap，t-SNE和LDA降维结果四类样本混叠严重，无法有效将四类样本分离开，降维效果最差；W-Isomap和S-Isomap可将四类样本基本分离，但磨损状态与正常状态存在样本混叠现象，且各类样本较为分散，降维效果较差；ISSL-Isomap可将四类样本完全区分开，并且各类样本较为集中，降维效果最好。分析其原因在于：Isomap和t-SNE为无监督流形学习方法，降维过程未考虑样本标签信息，不太适合行星齿轮箱故障信号这类存在诸多奇异数据点的情况；LDA为线性监督型降维方法，不能有效对非线性故障特征进行维数约简；W-Isomap，S-Isomap为监督型流形学习方法，能够基本将各类样本分离开，但这两种算法仅考虑样本空间位置，因此降维效果不如综合考虑样本空间位置和夹角信息的ISSL-Isomap算法。综上验证利用ISSL-Isomap对多域故障特征进行降维处理的有效性。

表2 单域和多域特征提取效果

为量化上述6种方法降维效果，从降维性能指标和故障识别精度两方面进行分析。其中，将类间距与类内距的比值作为降维性能指标，比值越大，表明同类样本越集中，异类样本越分散；将各算法特征压缩结果分别输入至ABC-SVM多故障分类器中进行识别，6种算法的降维效果如表3所示。

(a) Isomap降维后的三维可视化结果

(b) t-SNE降维后的三维可视化结果

(c) LDA降维后的三维可视化结果

(d) W-Isomap降维后的三维可视化结果

(e) S-Isomap降维后的三维可视化结果

(f) ISSL-Isomap降维后的三维可视化结果

表3 6种算法降维性能指标和故障识别精度

由表3可知，ISSL-Isomap算法有着最大降维性能指标和最高故障识别进度，进一步验证ISSL-Isomap对多域故障特征进行降维处理优越性；所提“SSO-VMD+多域故障特征+ISSL-Isomap+ABC-SVM”故障诊断模型对行星齿轮箱不同工况的故障识别率达到100%，能够精准的将四类样本区分开，以此验证该模型的有效性。

最后，为验证ABC-SVM多故障分类器进行模式识别的优越性，将其与粒子群优化支持向量机(Particle Swarm Optimization Support Vector Machine, PSO- SVM)[20]多故障分类器进行对比，将6种算法的降维结果(横坐标1, 2, 3, 4, 5, 6分别表示Isomap, t-SNE, LDA, W-Isomap, S-Isomap以及ISSL-Isomap)分别输入至两种分类器中进行识别，其中每类工况训练样本与测试样本按4:6随机分配；PSO-SVM中粒子群规模为20，终止迭代为100，局部搜索能力为2，全局搜索能力为2，将训练样本3折交叉后的平均识别率定为适应度函数，2种分类器对6种特征提取方法的测试样本识别结果如图12所示。据图12可知：2种多故障分类器对“SSO-VMD+多域故障特征+ISSL-Isomap”的特征提取均达到100%，验证了所提特征提取方法的优越性；与PSO-SVM多故障分类器相比，ABC-SVM多故障分类器对6种方法特征提取结果的测试样本平均识别率均为最高，验证了利用ABC-SVM进行故障诊断识别的优势。

图12 2种分类器对比

4 结 论

(1) 提出一种参数优化变分模态分解算法——SSO-VMD，将樽海鞘群算法应用于VMD的参数选取问题，仿真实验结果表明该方法能够避免EMD的模态混叠和过分解现象，并且SSO算法能有效搜索出VMD的全局最佳参数。

(2) 建立一种基于参数优化变分模态分解和多域流形学习的行星齿轮箱故障诊断模型，故障诊断实验表明：多域特征提取方法优于时域、频域、尺度域等单域特征提取方法；ISSL-Isomap降维效果优于Isomap，t-SNE，LDA，W-Isomap和S-Isomap等算法；ABC-SVM分类器的识别效果优于现有的PSO-SVM分类器；所提故障诊断方法的故障识别率达到100%，可以有效、精准的诊断出行星齿轮箱各故障类型。