PCM泡沫铝/液冷复合式锂电池热管理

安治国，陈 星，田茂飞，赵 琳，司 鑫

(重庆交通大学 机电与车辆工程学院，重庆 400074)

0 引 言

大量研究表明，空气污染对人类健康和生态环境的危害日渐显著，解决这一问题迫在眉睫[1]。电动汽车可有效减少城市噪音污染，改善空气质量，从而被大力推行。动力电池被喻为电动汽车的“心脏”，其性能的优劣直接决定汽车的安全、行驶效率和行驶里程。锂电池利用其无记忆性、高比功率、高能量密度、高循环次数等优势已成为当前电动汽车供能核心。但锂电池性能易受温度影响，为保证电池具有长的使用寿命和稳定的运行性能并防止其发生热失控(温度超过60 ℃)甚至爆炸，需将锂电池充、放电运行工况下的温度保持在20～50 ℃之间[2-4]。此外，电池组温度分布不均将导致各锂电池间性能衰退不同，迫使电池组容量减退加剧，运行性能大幅下降，故电池组温差应控制在5 ℃以内[5,6]。因此，针对锂电池散热问题设计一个高效、可靠的散热方案是不可或缺。

基于相变材料高潜热、低成本、几何形状可变等特性的考虑，部分学者已将其应用于不同形式的被动散热方案中，并充分展现了相变材料散热的优势。S. AL-HALLAJ等[7]率先运用石蜡混合物作为相变材料，并将该相变材料包裹电池以吸收电池释放的热量，相较传统风冷散热而言相变材料展现出更好的散热性能和均温性能；N. JAVANI 等[8]研究了不同厚度的PCM(0、3、6、9、12 mm)对方形单体电池散热的影响，研究表明PCM可有效控制电池温度且PCM越厚电池温度越低。

但PCM存在低导热系数的缺点，迫使其应用受到严重限制，为弥补这一不足，PING Ping等[9]将PCM填充在带有翅片的散热框架中；LIN Chunjin等[10]将膨胀石墨和PCM相结合并添加石墨板片构成电池组散热系统，在短途行驶中(小于10 km)可有效控制电池组温度；XIE Yongqing等[11]，WANG Xiaoming等[12]等将泡沫铜/石蜡混合物和风冷相结合，研究了风量、液相率、导热板厚度等因素对散热系统的影响，得到相变材料/风冷复合式散热性能远优于纯风冷散热性能的结论；JIANG Guiwen等[13]将包裹了膨胀石墨/石蜡混合物的电池排列在带有挡板的铝壳中并加以强制风冷构成电池组散热系统，研究表明，挡板可改变空气流向从而增加传热效率。以上研究从不同散热方式和结构方面分析了电池组在充放电运行工况下的散热性能，但热管理系统在空间利用率低、散热结构复杂、加工难度大等方面的不足仍存在。特别是，当锂电池在极端工况下(高环境温度、高倍率放电)运行时，有效对电池组进行散热的研究还不充分。

为弥补上述研究的不足，笔者提出PCM泡沫铝/液冷复合式散热模型，在环境温度为40 ℃、放电倍率为3C条件下，利用有限元法对散热模型进行数值模拟并采用响应面法分析PCM泡沫铝的孔隙率、流道间距和液体流速对电池组温度的影响。

1 模型与方法

以松下NCR18650PF锂电池为研究对象，其规格参数如表1。电池模组由25颗单体电池(5S5P)和散热结构组成。运用Pro/Engineer建立散热结构三维模型并对其采用四面体网格进行划分，电池组网格模型如图1(a)。散热模型由PCM泡沫铝结构(厚度为2 mm)、电池、铝制框架(134 mm×134 mm×65 mm)3部分组成，铝制框架可提高散热体的导热能力并防止融化的PCM泄露。铝框带有两条U型管道，流道的排布和液体进出口方式如图1(b)；孔直径为3 mm；以铝框的中心面为基准，两流道圆心间的距离为D(D取7、20、33 mm)；选用水作为冷却介质。

表1 锂电池规格参数Table 1 Specifications of lithium-ion battery

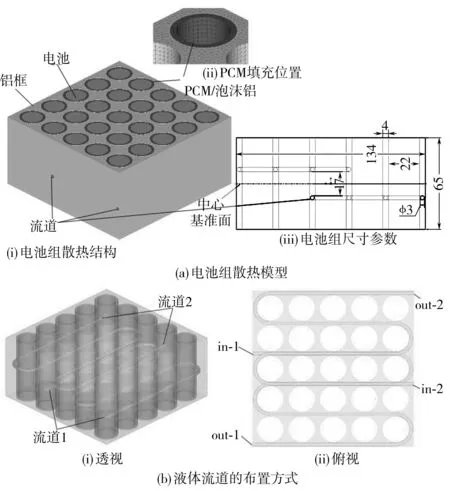
图1 电池组网格模型Fig. 1 Battery mesh model

2 数学模型

2.1 电池生热模型

锂电池在运行过程中其内部会发生电化学反应，从而产生大量的热。Lump-capacitance模型可全面展现电池的热性能，故笔者选用此模型描述锂电池的生热[14-17]。假设锂电池内部生热恒定且均匀；各种材料属性均表现为各向同性且介质均匀；放电时电池内部各处电流密度均匀且忽略热辐射。那么电池的比热容、密度和导热系数等物性参数均为常数，则电池内部能量守恒公式为：

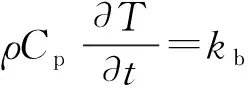
(1)

式中：ρ为电池密度；Cp为电池比热容；kb为电池导热系数；T、t分别表示局部温度和时间；Q为不可逆反应焦耳热和可逆反应熵热之和，表示电池生热速率，如式(2)：

(2)

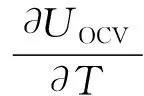
(3)

式中：q为电池单位体积的生热速率；V为电池体积；RJ为电池焦耳内阻。3 C放电倍率下，q=124 016.3 W/m3。

2.2 PCM模型

所用相变材料为石蜡RT44HC，其物性参数见表2。运用文献[19]中的焓变法仿真PCM的热传递，能量公式为：

表2 混合相变材料的物性参数Table 2 Physical properties of composite phase change material

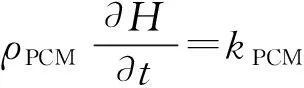
(4)

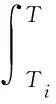
(5)

(6)

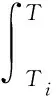
2.3 初始和边界条件

初始条件为：t=0;T(x,y,z)=T0。基于牛顿冷却定律可将电池表面与周围环境间的对流换热表示为：

Qc=h(Ts-To)

(7)

式中：Qc为单位面积的对流换热量；h为对流换热系数，据文献[20]，取自然对流换热系数为5 W/(m2·K)；Ts、To分别为电池表面温度和环境温度。

此外，管道内液体的能量守恒、质量守恒及动量守恒公式分别为：

ρlCpl+(ρlCplvT)=(klT)

(8)

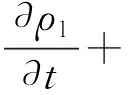
(9)

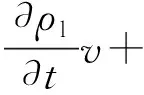
(10)

式中：ρl、Cpl及kl分别为液体的密度、比热容和导热系数；v和p为流体的流速和静压力；μ为液体黏性系数。

在ANSYS/FLUENT软件中，设定散热模型初始温度为313.15 K，流体采用速度入口和压力出口边界条件，模型外表面为自然对流散热。

3 结果与讨论

3.1 模型仿真可靠性验证

为保证仿真模型的可靠性,对散热模型进行网格独立性验证。3C放电，流速为0.04 m/s，PCM泡沫铝孔隙率为84%时，不同流道间距下复合式散热模型温差随体网格数量的变化曲线如图2。从图2中可知，当散热模型网格数量从780 000增至1 500 000 时，其温差几乎保持在同一直线上，电池组温差波动最大值仅为0.15 K，出现在流道间距为7 mm散热模型中。结果表明，电池组模型网格数量的改变对仿真结果无明显影响，故该仿真模型可靠。为保证仿真精度和减少仿真时长，对流道间距为7、20、33 mm的散热模型选择网格数量分别为974 030、984 030、994 030的模型用以仿真。此外，为保证仿真的精确性，笔者还考虑了仿真步长对结果的影响。3C放电倍率下，时间步长设置为1 s与3 s时散热模型的最高温度误差仅为0.02 ℃。因此，步长对仿真结果没有明显影响，为缩短仿真时间将步长设定为3 s。

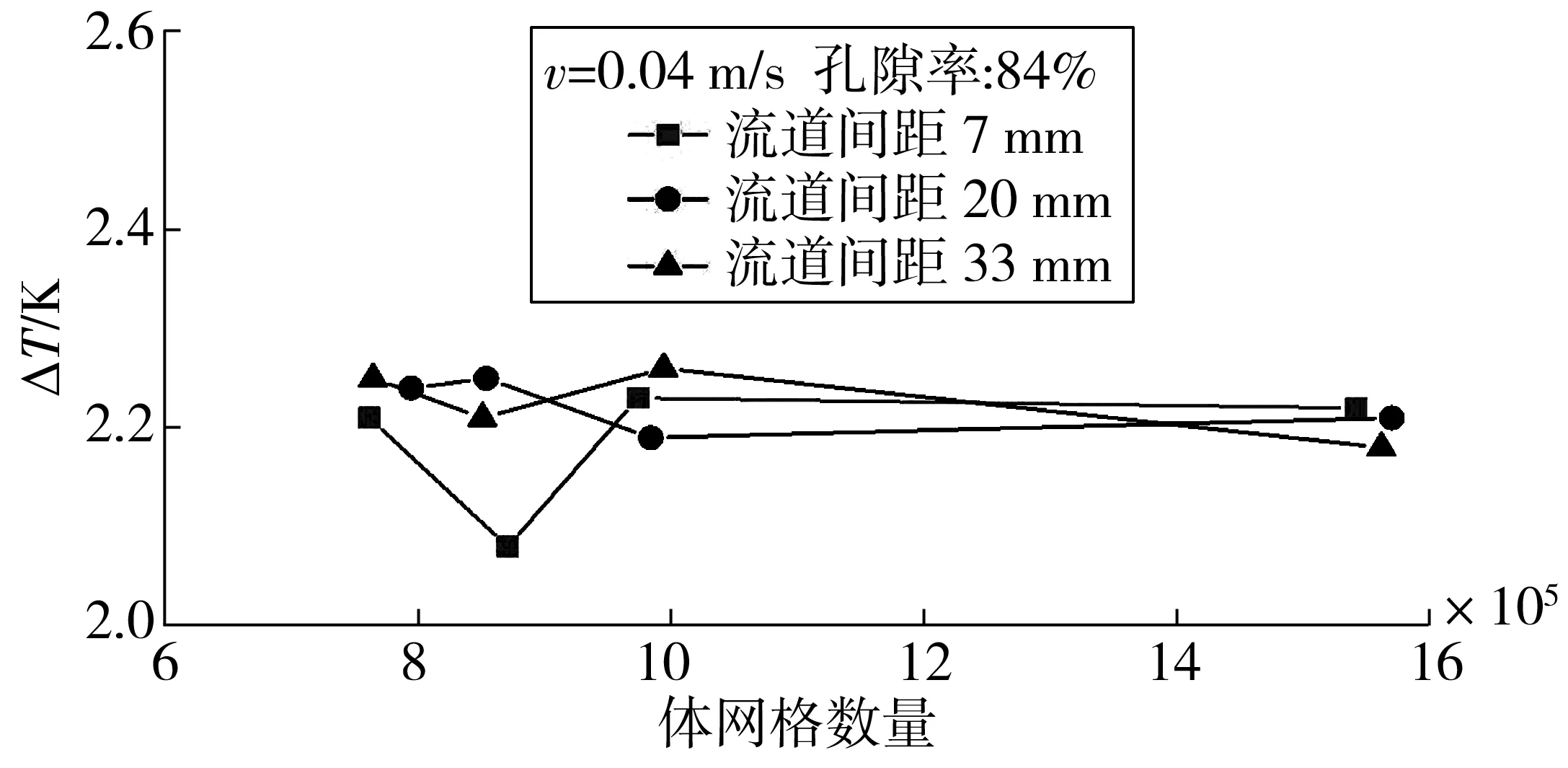
图2 散热模型温差随体网格数量变化的曲线Fig. 2 Curves of the temperature difference of the each heat dissipation model changing with different number of meshes

3.2 被动散热性能分析

电池组初始温度与环境温度均为313.15 K、散热系统未加液冷条件下不同放电倍率下电池组温度分布如图3。

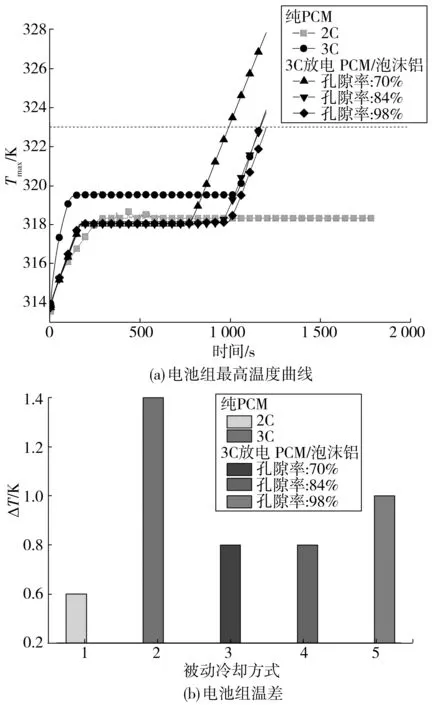
图3 不同放电倍率下被动散热时电池组温度分布Fig. 3 Temperature distribution of battery pack with passive heat dissipation at different discharge rates

当采用纯PCM冷却时，2C放电倍率下，放电终止时电池组最高温度为318.3 K，温差为0.6 K，可将电池温度控制在安全范围内；当锂电池放电倍率升至3C，放电前1 000 s内，PCM利用其高潜热特性可吸收电池发出的热量并将温度平衡在319.5 K，其液相率小于50%；当放电时长至1 000 s后，PCM不能充分吸收电池热量，电池组最高温度升至 323.9 K，超出电池安全运行范围。当采用PCM泡沫铝冷却时，3C放电倍率下，放电终止时孔隙率为70%、84%、98%的电池组模型最高温度分别为327.8、323.7、323.0 K，均大于或等于323.0 K，超出电池安全运行范围。结果表明：在2C放电倍率下，PCM利用其高潜热的特性可有效吸收电池释放的热量并通过铝制框架散热从而将电池温度控制在安全范围内且电池组温度分布均匀；当放电倍率增至3C，全被动散热模型不能满足电池组散热要求，需辅以主动冷却。

3.3 主动散热性能分析

环境温度与电池组初始温度保持一致，均为313.15 K，热管理系统未添加PCM泡沫铝，电池表面直接与铝制框架接触。图4展示了不同放电倍率下电池组温度分布。当2C放电、流道间距为7 mm、液体流速0.08 m/s条件下，放电终止时电池组最高温度和温差分别为318.6 K和0.9 K，满足散热要求；当放电倍率增至3C，流道间距为7、20、33 mm条件下，放电终止时电池组最高温度分别为324.1、323.9、323.9 K，均大于323 K，不满足散热要求。

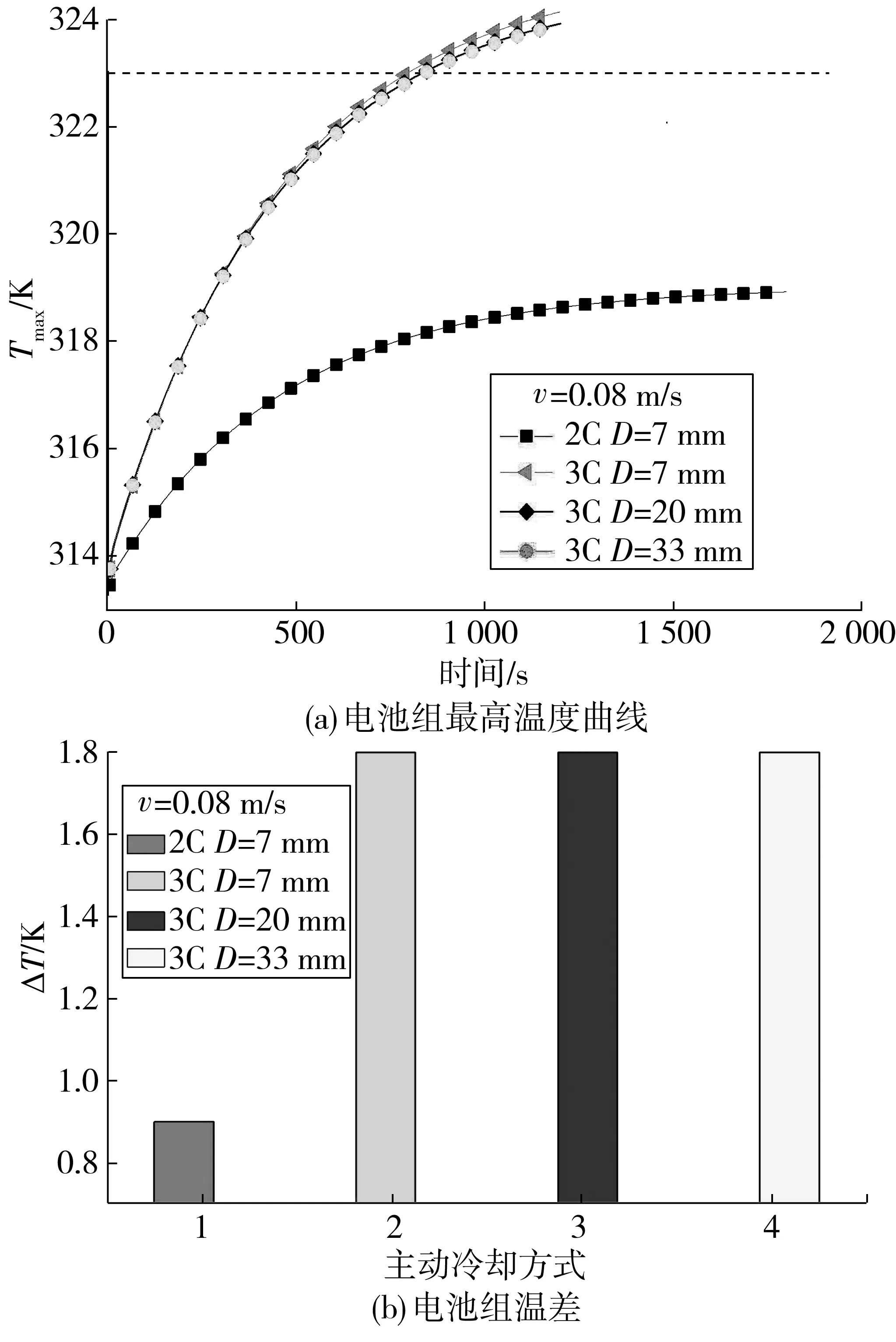
图4 不同放电倍率下主动散热时电池组温度分布Fig. 4 Temperature distribution of battery pack with active heat dissipation at different discharge rates

3.4 PCM泡沫铝/液冷复合式散热性能分析

从上述分析可知，只采用被动或主动散热方式，电池组不能满足散热要求。因此笔者提出PCM泡沫铝/液冷复合式散热方式，并运用响应面法分析PCM泡沫铝的孔隙率、流道距离、液体流速三因素对电池组最高温度和温差的影响。

3.4.1 复合式散热实验方案和因素水平设计

基于Box-Benhnken实验设计原理，应用响应面法在三因子三水平上对复合式散热模型参数的选取进行优化。X1、X2、X3分别为PCM泡沫铝孔隙率、流道距离、液体流速；Y1、Y2分别为电池组最高温度(Tmax)和电池组温差(T)。实验因子和水平见表3，试验方案与实验结果如表4。

表3 响应面分析因子及水平Table 3 The analysis factors and levels of response surface methodology

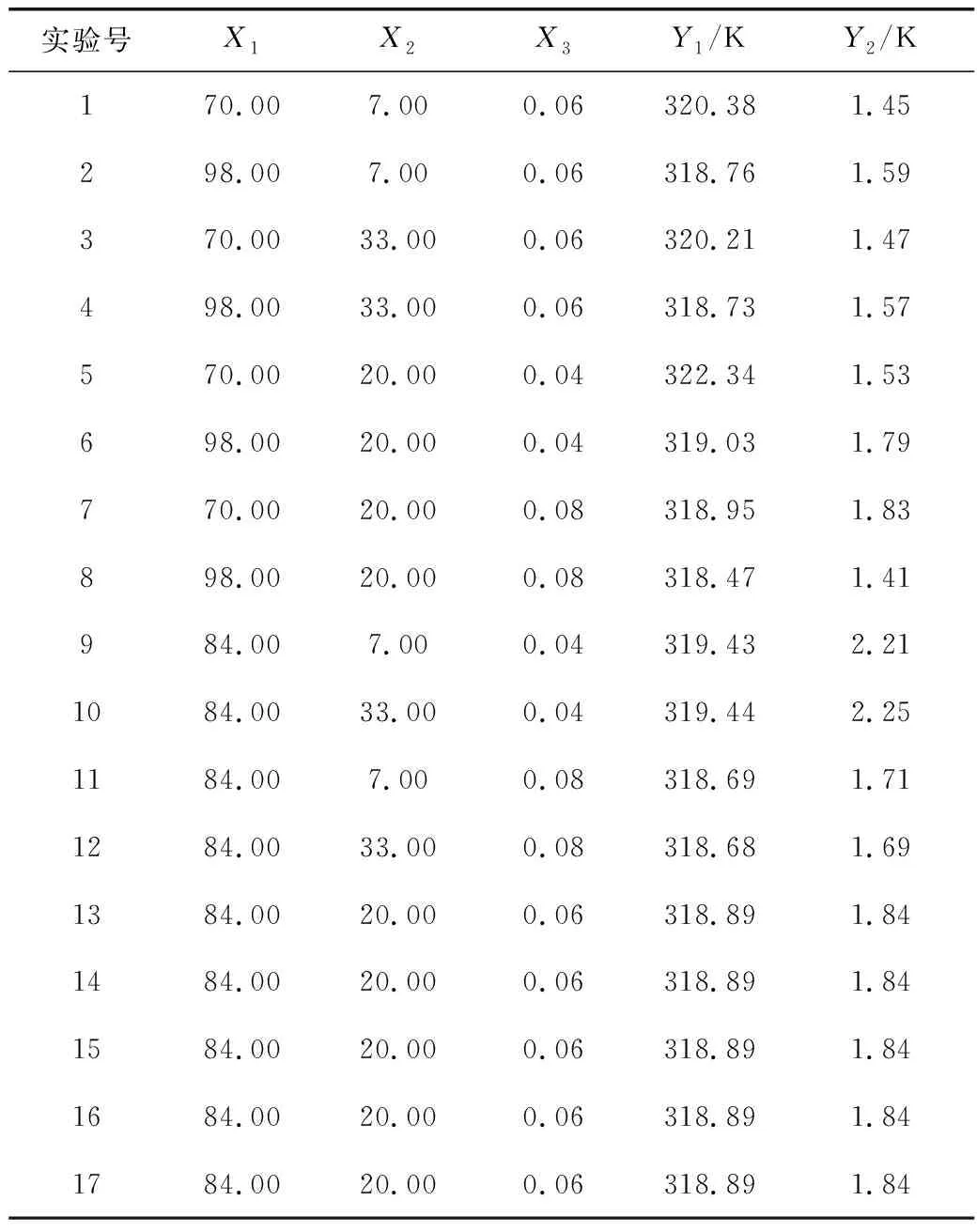
表4 响应面分析方案及实验结果Table 4 The scheme and experimental results of response surface analysis

表4中实验号为1～12和13～17分别为析因实验和中心实验。17个实验点中有析因点和零点之分，其中零点为区域的中心点，零点实验重复5次，用以估计实验误差析；而析因点则是自变量取值在X1、X2、X3所构成的三维顶点,。

3.4.2 响应面分析方案及结果

采用SAS RSREG程序对所得数据进行ANOVA和二次响应面回归分析，分别得到多元二次响应方程：

Y1=318.89-0.86X1-0.025X2-0.68X3+

(11)

(12)

两模型的P值均小于0.05且R2分别为94.32%、84.53%，表明该实验方法是可靠的，可运用该方程模拟真实的三因子三水平分析。图5和图6分别为PCM泡沫铝孔隙率与液体流速对电池组最高温度和电池组温差的响应曲面。

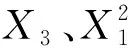
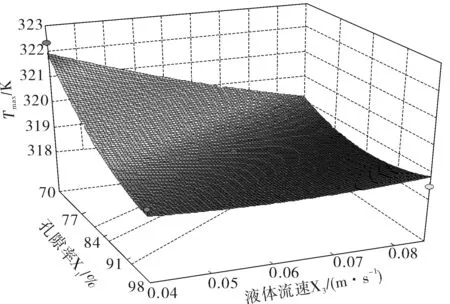
图5 PCM泡沫铝的孔隙率和液体流速对电池组最高温度的响应面Fig. 5 Response surface of the porosity of PCM aluminum foam and liquid velocity to the maximum temperature of the battery module

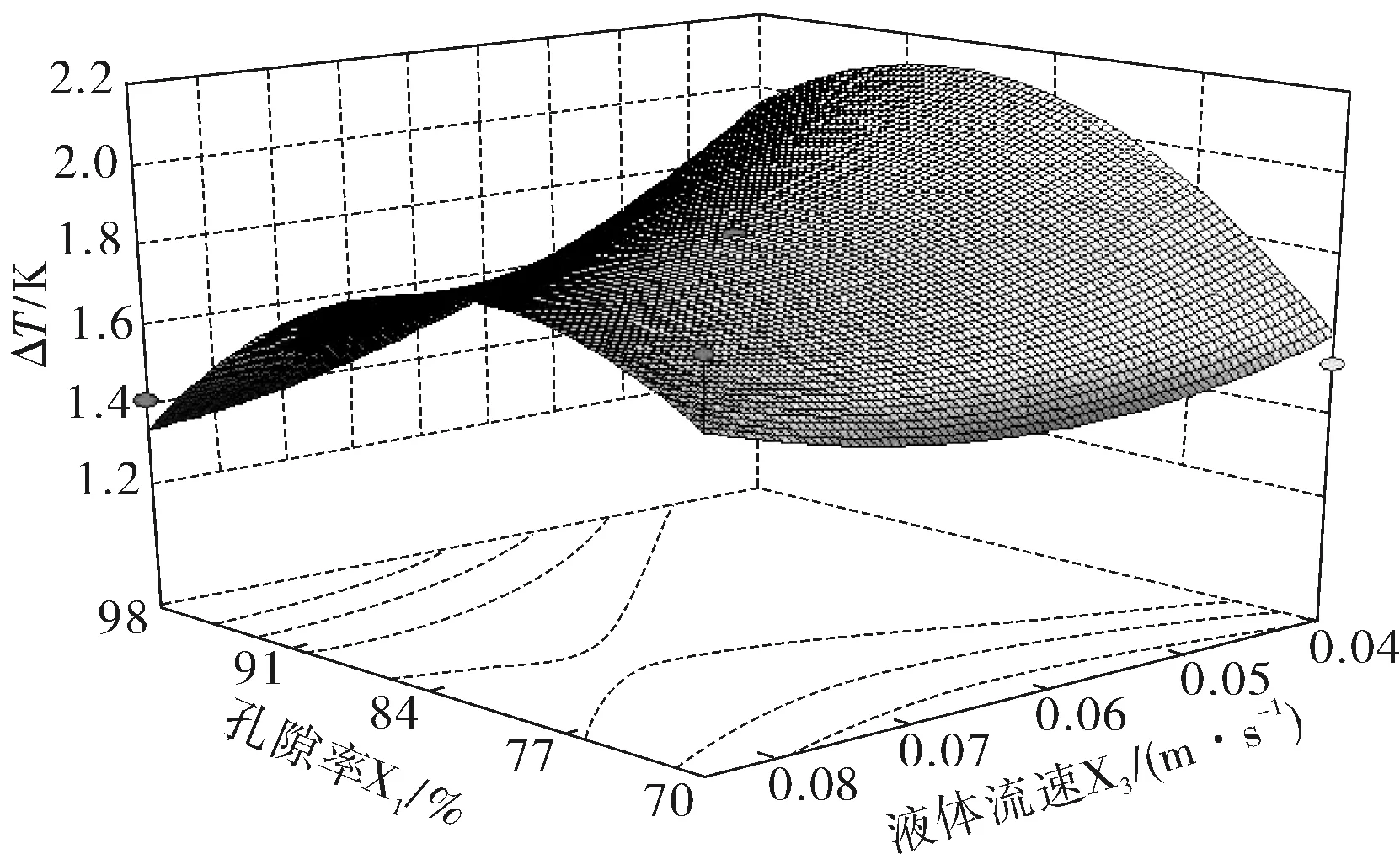
图6 PCM泡沫铝的孔隙率和液体流速对电池组温差的响应面Fig. 6 Response surface of the porosity of PCM aluminum foam and liquid velocity to the temperature difference of the battery module

3.4.3 主/被动及复合式散热方式的比较

由响应面法分析可知，当PCM泡沫铝孔隙率、流道距离及液体流速分别取98%、20 mm、0.08 m/s时，复合散热系统有最优散热性能，此时电池组的最高温度为318.5K，比纯被动和纯液冷散热方式的最高温度323.0、323.9 K分别降低了4.5、5.4 K，且电池组温差只有1.4 K。当液体流速仅为0.04 m/s，PCM泡沫铝孔隙率、流道距离分别为98%和20 mm时，电池组的最高温度和温差分别为319.0 K和1.8 K，已满足散热要求，且比纯被动和纯液冷散热方式的最高温度分别降低了4、4.9 K，故复合式散热结构体现了良好的散热性能。环境温度为313.15 K时，不同散热方式下的电池组温度云图如图7。

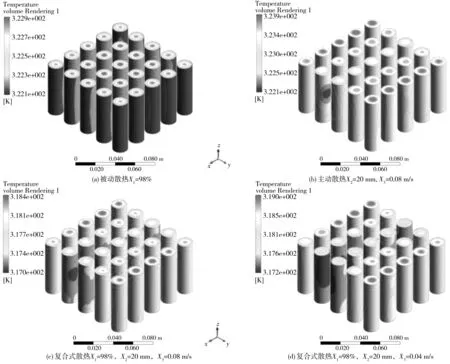
图7 不同散热方式下电池组温度云图Fig. 7 Temperature nephogram of battery module under different heat dissipation modes

4 结 论

研究了环境温度为313.15 K、不同放电倍率条件下，PCM泡沫铝散热和液冷散热时电池组最高温度分布情况，得到3C放电倍率下，只采用PCM泡沫铝散热或液冷散热均不能满足电池组散热要求的结论，因此将PCM泡沫铝和液冷相结合并通过响应面法分析了PCM泡沫铝孔隙率、流道间距、液体流速三因素对PCM泡沫铝/液冷复合式散热系统的影响，得出如下结论：

1)PCM泡沫铝孔隙率、液体流速对电池组最高温度影响显著。当孔隙率和液体流速增加时，电池组最高温度呈减小的趋势，但当孔隙率大于84%，液体流速大于0.06 m/s后，电池组最高温度趋于稳定。

2)液体流速对电池组温差影响显著，增加液体流速可有效减小电池组温差。当流速为0.08 m/s时电池组温差仅为1.4 K。

3)复合式散热系统表现出良好的散热性能。当液体流速低至为0.04 m/s，电池组的最高温度和温差分别为319.0 K和1.8 K，已满足散热要求。