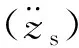双横臂悬架动力学建模及模糊滑模控制器设计
2021-01-18赵强,孙政
赵 强,孙 政
(1. 东北林业大学 交通学院,黑龙江 哈尔滨,150040; 2. 聊城大学 机械与汽车工程学院, 山东 聊城, 252059)
0 引 言
悬架系统对车辆的平顺性和操纵稳定性具有较大影响。为提高车辆的整体性能,一些中高端汽车上已配备了主动悬架。双横臂悬架常被作为前悬架安装使用,以提高汽车的行驶平顺性,其运动学特性的优劣直接影响汽车的平顺性。由于双横臂悬架结构相对复杂,组成结构对悬架系统影响较大,导致直接使用悬架系统物理参数建模的传统简化模型准确性进一步下降[1]。
研究表明[2-3]:麦弗逊悬架在1/4车的二自由度模型简化过程中,直接使用悬架系统物理参数值建模能基本反映悬架振动特性。但对结构复杂的双横臂悬架,直接使用悬架系统组件的物理参数值简化模型,与实际双横臂悬架的1/4汽车模型(三维多体动力学模型)求得的响应相差较大,这使得对双横臂悬架的动力学建模具有重要意义。
宋晓琳等[4]及朱柏霖[5]利用参数辨识的方法,识别出主动双横臂悬架简化模型的相关参数值,验证了采用参数辨识法得出的简化模型,能较好的反应双横臂悬架的实际运动,增强了控制算法的实用性。目前,主动悬架的控制算法主要有:模糊控制[6]、反步法[7]和滑模控制[8-9]等,以上对双横臂悬架进行建模仿真的研究中,并没有考虑到悬架的具体结构对悬架的影响,使得设计的控制算法的实用性有待检验。P.B.KRISHN[10]建立了基于双簧臂悬架的 1/4汽车二维模型,进行了运动和动力学响应分析,最后通过搭建的1/4 汽车悬架试验台验证了模型的准确性。
笔者在文献[10]的基础上,通过对双横臂悬架的机构动力学进行建模和分析,计算悬架阻尼系数和弹簧刚度的等效系数,并与传统的双横臂悬架简化模型做了对比。在此基础上建立主动双横臂悬架1/4模型,设计基于模糊切换增益调节的滑模控制器,通过simulink仿真分析并与PID、被动悬架的仿真结果进行对比,验证笔者中所设计的控制方法。
1 动力学建模及1/4等效模型
双横臂悬架系统的结构可以抽象为图1机构:包括上横臂(EF)、下横臂(AB)、阻尼器与弹簧(通过滑柱(GH)与上下横臂连接)、主销(BF)。图1中ks为弹簧刚度系数,cs为阻尼器阻尼,簧载质量为ms,非簧载质量为mu,kt、ct分别为轮胎的垂向刚度系数和阻尼系数,ktl为轮胎侧偏刚度。

图1 双横臂悬架的机构Fig. 1 Schematic diagram of the double wishbone suspension
假设主销(BF)与上、下横臂的连接点B、F,以及车轮轴中心O在笛卡尔坐标系中初始坐标分别为(By0,Bz0)(Fy0,Fz0)(Oy0,Oz0)。由欧拉角变换可得式(1):
(1)
式中:Oz=Oz0+zu;Oz0为O点初始z轴坐标;zu为车轮垂直位移;Fy、Fz,Oy、Oz、By、Bz分别为F、O、B点处瞬时x、y、z轴坐标。
为了将悬架系统运动学关系与动态响应相关联,可在运动学线性系统中做如下处理:当车轮外倾角α较小时,sinα=1,cosα=α,由一阶泰勒级数可近似求得式(2):
(2)
式中:zs为簧上质量位移。
由式(2)可求得Oy,Fy,Fz,By,Bz。
应用拉格朗日方程建立系统的运动微分方程,动能T和势能V表示如式(3):
(3)
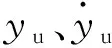
δl、δzt分别是悬架与轮胎的变形量如式(4)、(5):
δl=lGH-[(Gy-Hy0)2+(Gz-(Hz0+zs))2]1/2
(4)
δzt=zu-z0
(5)
式中:lGH为滑柱的初始长度;Hy0与Hz0为悬架的初始坐标点;Gy,Gz为G点处瞬时y,z轴坐标。
悬架中阻尼器产生的耗能D如式(6):
(6)

双横臂悬架的简化双质量线性二自由度模型如图2,对应的动力学方程如式(7):
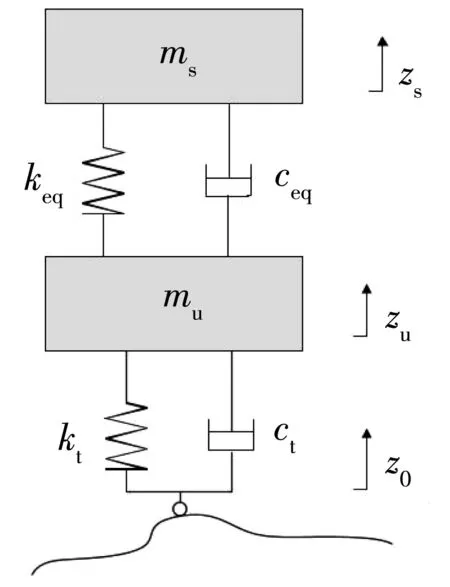
图2 双质量二自由度等效模型Fig. 2 Two-mass two-degree-of-freedom equivalent model
(7)
式中:keq、ceq分别为双横臂悬架的等效弹簧刚度和阻尼系数。利用keq和ceq分析悬架的运动效应比直接使用ks和cs更加准确。
根据式(3)给出keq、ceq具体推导过程。对于给定的车轮中心位移,悬架会相应地给出恢复力,如图3。通过滑柱沿轴向所产生的恢复力(ksδl)可知下横臂与轮轴关节B处的等效力FBF,如式(8):
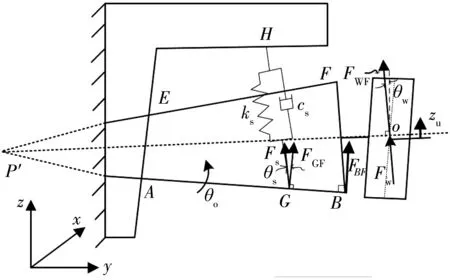
图3 车轮中心的等效力Fig. 3 Equivalent force at the wheel center
(8)
式中:θs为下横臂法线与滑柱夹角;lAG、lAB分别为A点到G、B点的距离。
作用于车轮轴中心的等效悬架力Fw,可通过悬架的瞬时旋转中心P′与FBF相关联。由于B、O都位于车轮主销上,故车轮中心O处的等效法向分量FWF与FBF关系如式(9):
(9)
式中:θo为下横臂旋转角;θw是力FWN和车轮固定轴之间的夹角。θo与θs的关系为lAGθo=δlcosθs。
车轮中心的等效垂直力如式(10):
(10)
当zu=0时,弹簧挠度δl是车轮垂直挠度zu的函数。θs和θw也是zu的函数,但是这些角度相对于zu的变化很小。假设这些角度变化不大,对车轮力求导可得到悬架等效刚度keq如式(11):
(11)
式中:φ为等效系数,联立式10-11,得:
(12)
滑柱变形对于zu的变化速率可以通过式(13)得出:
(13)
同样,车轮中心的等效阻尼力FWF如式(14):
(14)
故等效阻尼系数的表达式如式(15):
(15)
ceq=φcs
(16)
式(11)、(16)就是双横臂悬架的等效弹簧刚度和等效阻尼系数。至此,图2中双横臂简化模型的机构动力学建模完成。由图4可以看出:利用等效系数建立的双横臂悬架二自由度双质量简化模型的响应更加接近悬架的实际运动,使用此等效系数建立的等效简化模型,能更准确反应车辆在实际行驶过程中悬架的振动特性。
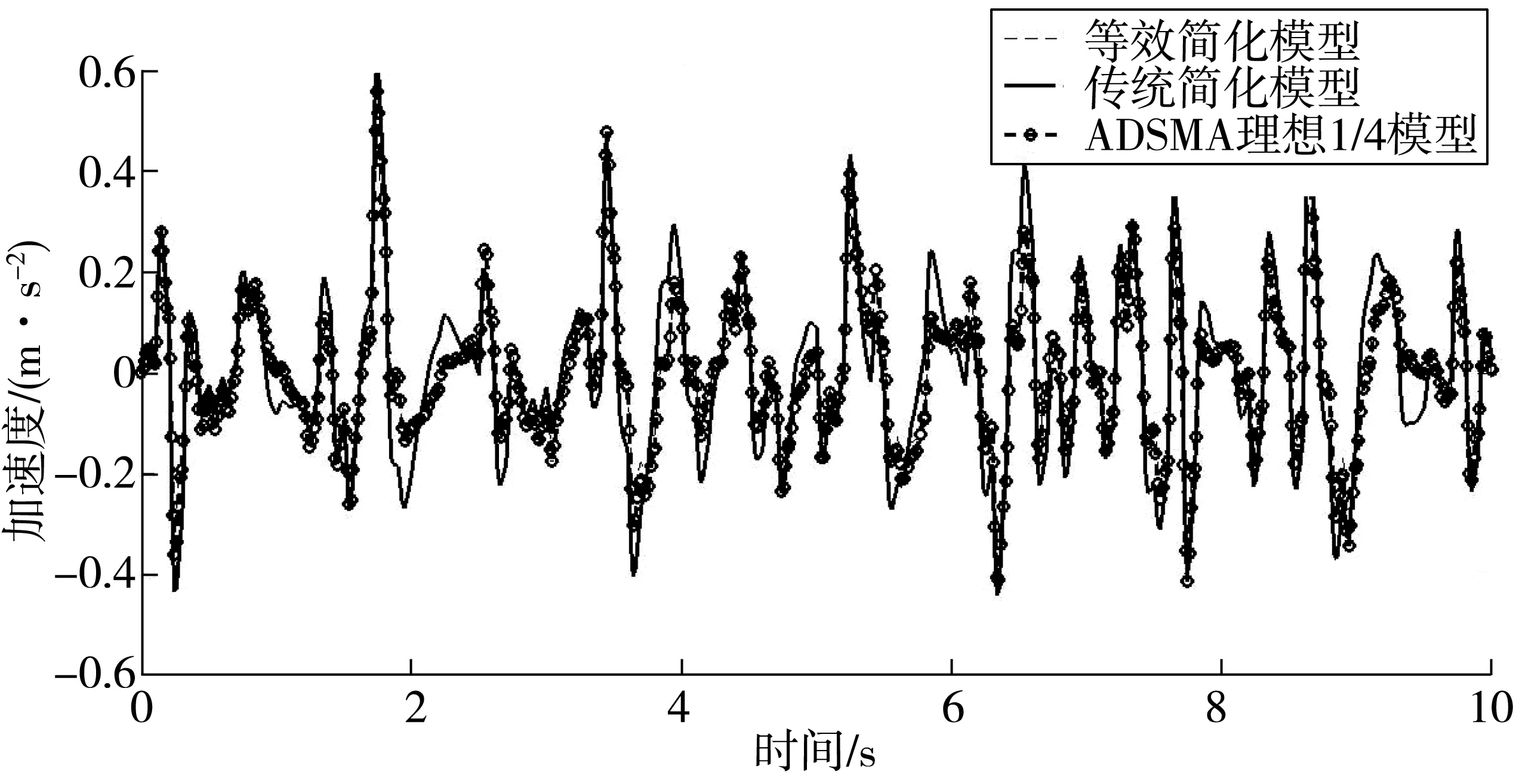
图4 模型加速度对比Fig. 4 Acceleration comparison of models
2 参考模型以及控制器设计
利用等效系数进一步建立主动双横臂悬架的二自由度简化模型,如图5。此模型以天棚阻尼控制为参考模型,主动作动器提供的主动力为Fd。
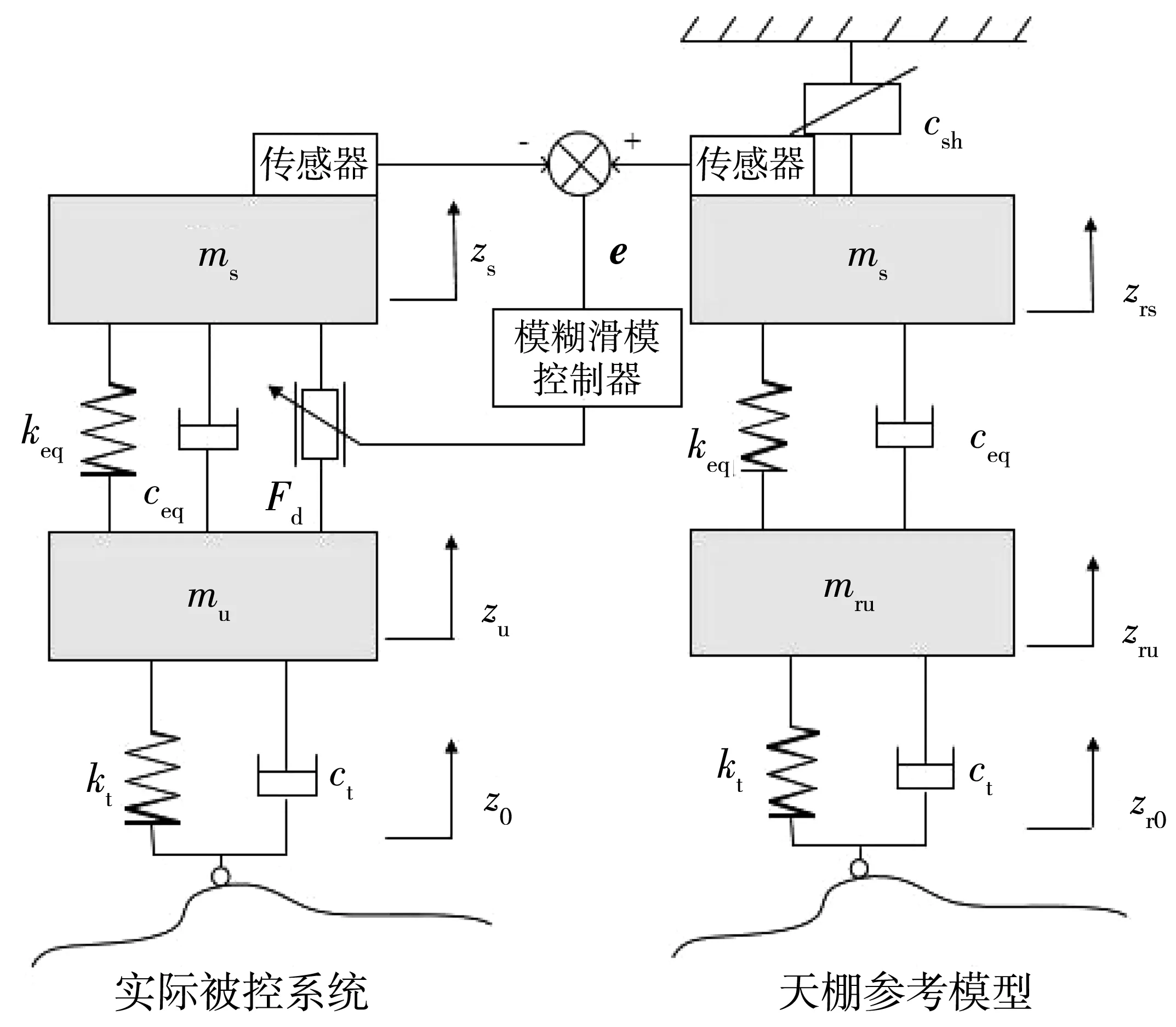
图5 实际被控系统与天棚参考模型Fig. 5 Actual controlled system and skyhook-based reference model
2.1 基于天棚阻尼控制的参考模型
天棚阻尼控制在悬架主动控制方面具有较好的效果[11],其思想是在悬架和假设的天棚间加入一个天棚阻尼器(图5),使实际被控系统的输出与天棚阻尼模型的输出作对比。
天棚阻尼参考模型的动力学方程如式(17):
(17)

(18)
式中:
Ar=
Dr=[0 0 0 0]T;ur=[z0]。
2.2 误差动力学系统的建立
模糊滑模控制原理是使实际被控系统跟踪参考模型的运动,使误差在控制器作用下尽可能接近参考模型,以达到控制目的。定义两个悬架系统的位移误差及积分以及速度误差为广义状态跟踪误差矢量e,即:
(19)
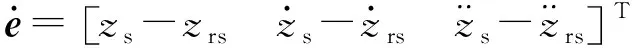
定义误差动力学方程:
(20)
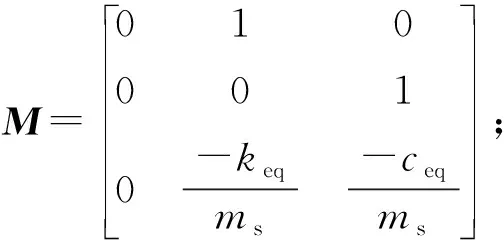
2.3 基于模糊切换增益调节的滑模控制器
对2.2中建立的误差动力学系统进行基于模糊切换增益调节的滑模控制,滑模切换函数如式(21):
s=ce=c1e1+c2e2+c3e3
(21)
式中:c为切换函数的导数向量,取c=[62.499 3 3.125 1]。
将误差动力学方程简化为式(21):
(22)
式(22)为滑动模态的运动方程,它决定了滑动模态的动态品质。
取控制系统进入滑模区域后的等效控制力ueq如式(23):
ueq=-[cB]-1c(A(t)e+g(t)X+H(t)Xr))
(23)
进一步整理得式(24):
(24)
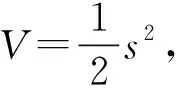
u=ueq+usw=ueq+K(t)mssgn(s)
(25)
综上所述,滑模控制器所解算出的主动控制力为式(26):
(26)
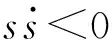
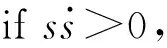
(27)
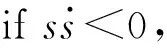
(28)
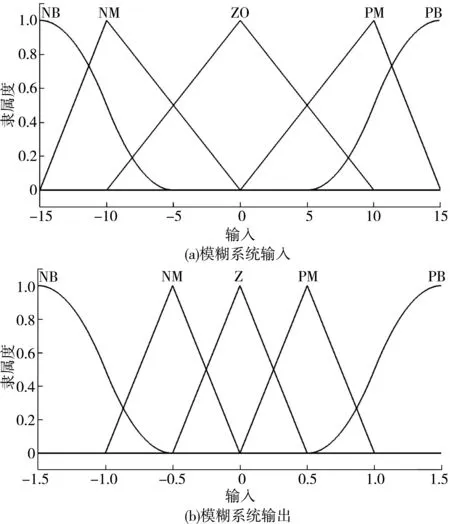
图6 模糊系统的输入、输出的隶属度函数Fig. 6 Membership function of input and output of fuzzy system

(29)
式中:g为比例系数。模糊滑模控制系统的结构如图7。
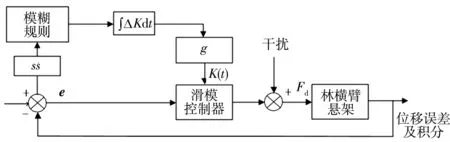
图7 模糊滑模控制系统结构Fig. 7 Fuzzy sliding mode control system structure
3 仿真试验及分析
为了验证模糊滑模控制的优化控制效果,运用MATLAB/simulink进行仿真验证,车轮受到的路面激励采用二级、三级路面加滤波白噪声方式得到如式(30):
(30)
式中:f0为路面输入的下截止频率;Gq(n0)为路面不平度系数;v为车辆速度;q(t)为输入高斯白噪声;n0为空间频率。系统仿真的具体参数设置如表1。
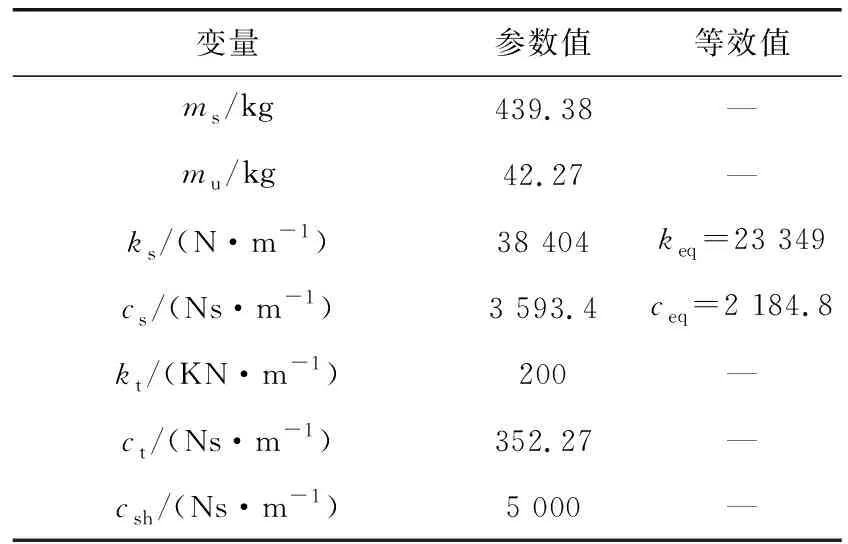
表1 系统仿体参数Table 1 System simulation parameters
对simulink中建立系统的动力学方程进行仿真,以验证设计控制器的控制效果。控制系统的simulink仿真框如图8。
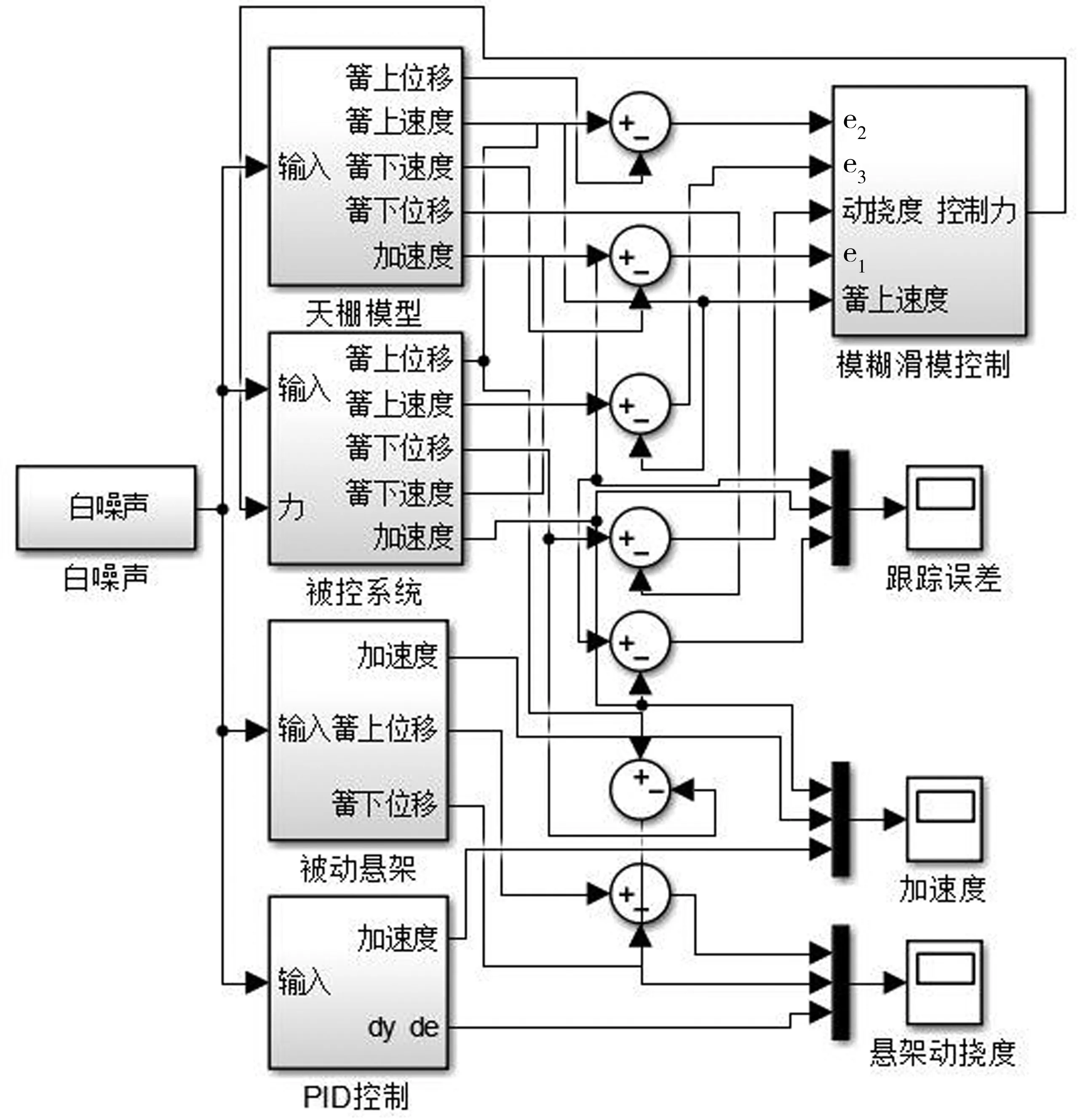
图8 控制系统simulink仿真模型Fig. 8 Control system Simulink simulation model
将模糊滑模控制和PID控制以及被动系统的各项特性进行比较。模糊滑模控制下的悬架与天棚参考模型的位移跟踪如图9。由图9可知,利用滑模控制器对天棚参考模型和实际被控系统的误差加以控制,被控系统可以有效地跟踪天棚参考模型,说明滑模控制具有较好的跟踪性能。
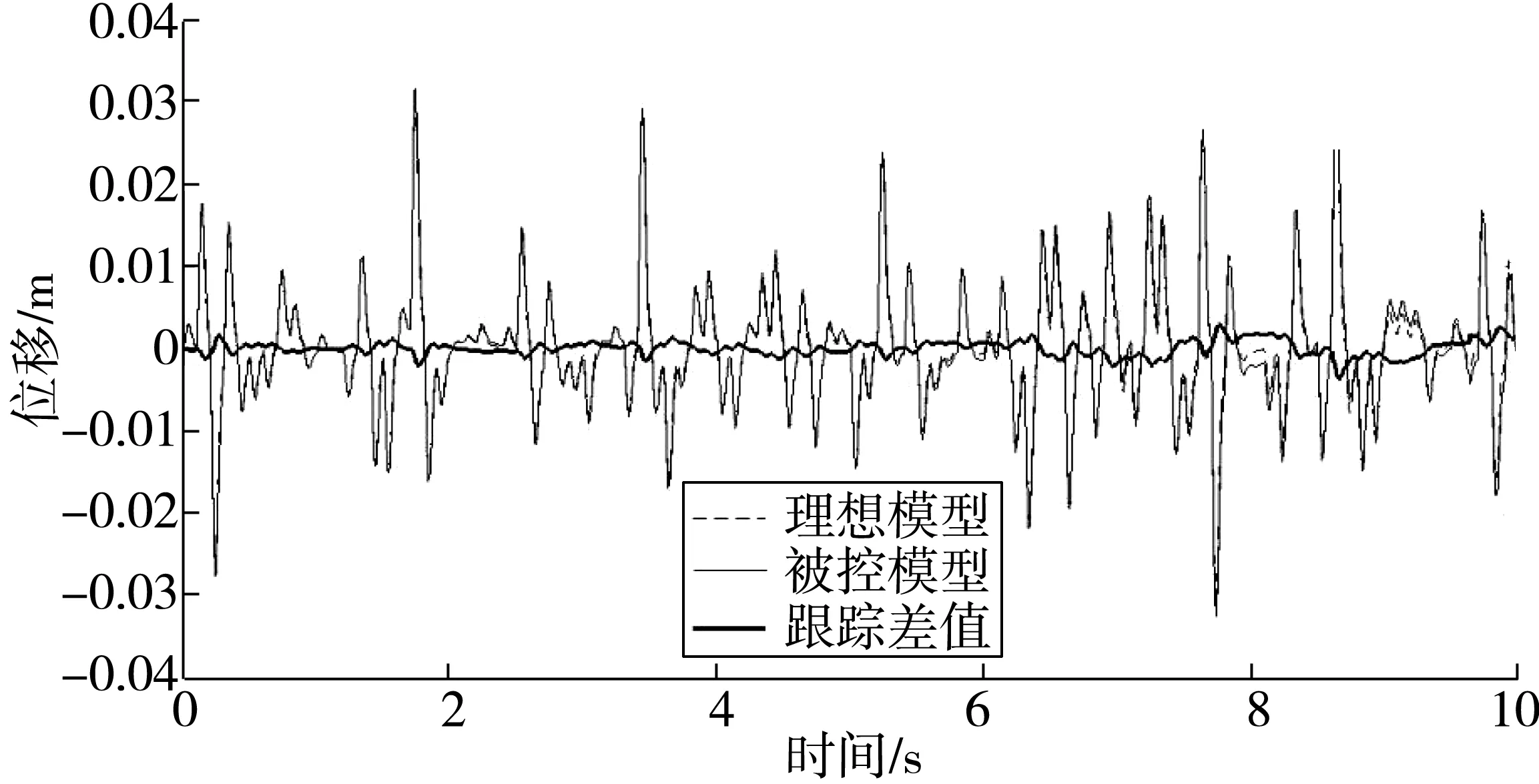
图9 实际被控系统与天棚参考模型的位移跟踪Fig. 9 The displacement tracking of the actual controlled system and the skyhook-based reference model
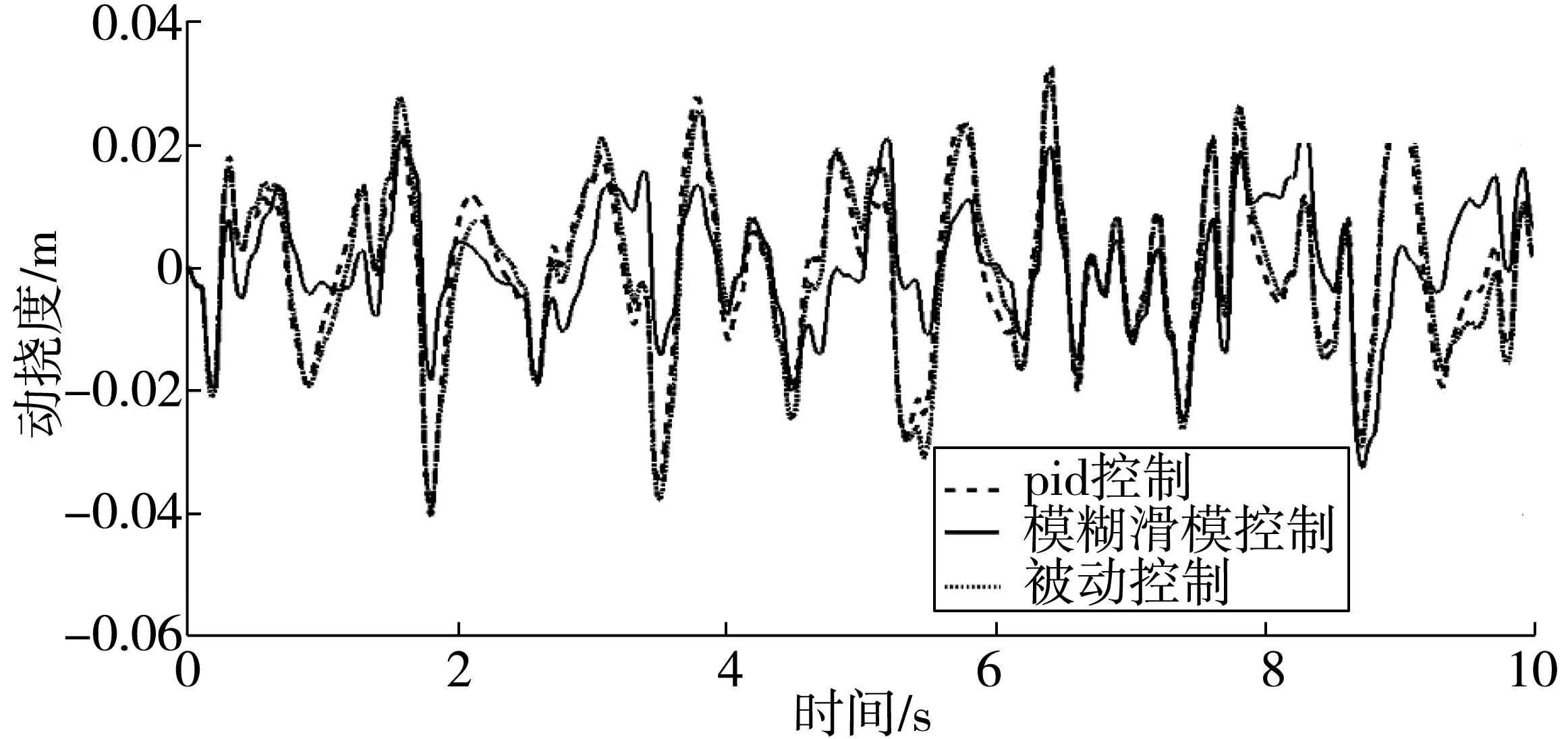
图10 悬架动挠度结果对比Fig. 10 Comparison of suspension dynamic deflection results
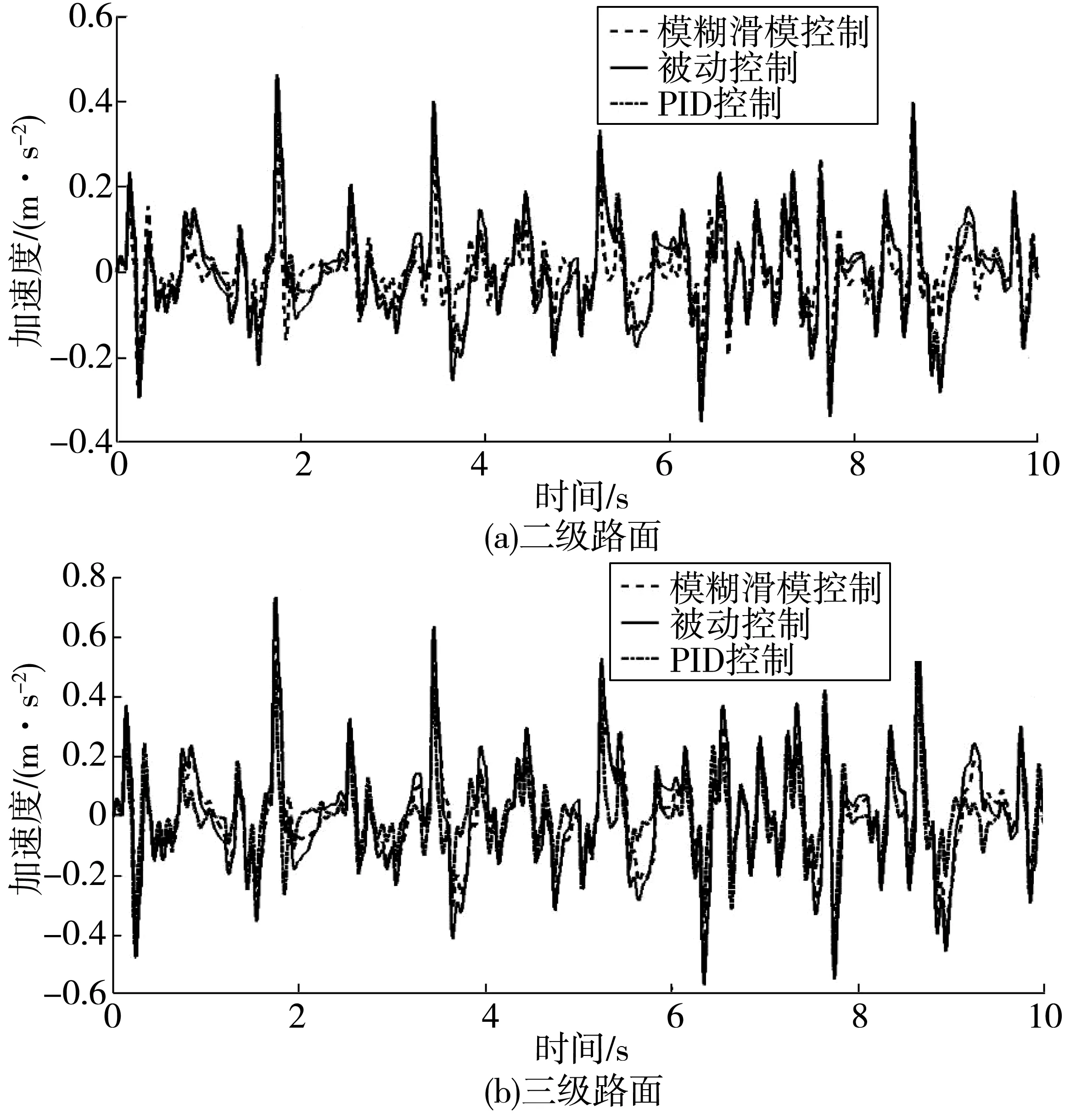
图11 二、三级路面下悬架加速度结果对比Fig. 11 Comparison of suspension acceleration results under second and third levels of road surface

图12 悬架加速度功率谱密度Fig. 12 Suspension acceleration power spectral density
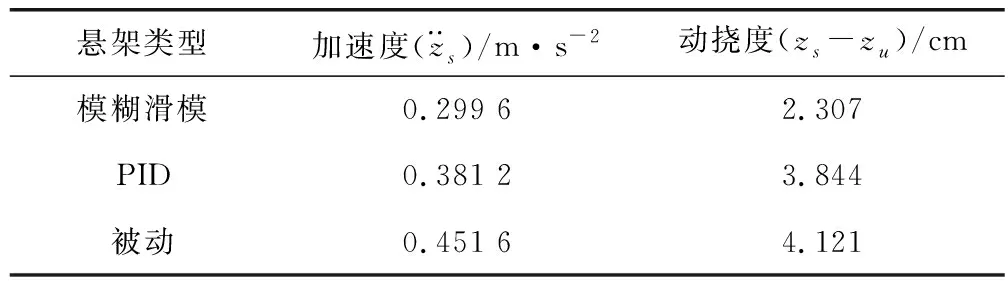
表2 二级路面不同控制方法下悬架系统性能最大值Table 2 Comparison of maximum performance of suspension system on secondary road surface under different control methods
4 结 语