采矿连续运输系统中矿仓容量的动态优化控制研究
2021-01-18白晓平
白晓平 赵 建
(西安建筑科技大学管理学院矿山系统工程研究所,陕西 西安 710055)
在采矿工程采运排的带式连续运输方式中,矿仓经常被设置。带式运输是以胶带、钢带、纤维带、塑料和化纤带等作为传送物料的运输方式通过设置矿仓,当仓前环节出现故障时,仓后环节可借助仓中的存料继续运转;而仓后环节出现故障时,仓前环节可借助仓中的空间继续向仓中存料。因此设置矿仓可以减少仓前和仓后环节的相互影响从而可以提高整个采矿工程中带式连续运输系统的可靠性。理论上设置矿仓有许多优点,如矿仓前和仓后环节的相互影响,缓冲不同运输流,调节和处理物料等。但在实践中因为设置矿仓后整个采矿工程中带式连续运输系统将变得非常复杂,所以这些优点可能并不能充分体现。在实际应用中,矿仓容量对整个采矿工程中带式连续运输系统的可靠性和生产效率有很大的影响,因此研究矿仓容量的可靠性和动态优化设计对其优点的充分发挥很有意义。
截至目前,已有许多文献研究矿仓(或叫贮仓、存储仓等)或矿山带式运输系统。在20世纪50年代,波兰的J.KERP教授将带有矿仓的运输系统命名为软连接系统,讨论了矿仓对整个运输系统的影响,但缺乏定量分析。文献[1]建立了一个仿真模型,用以对美国南Utah州一个地下煤矿的实际提升带式运输系统进行仿真,在仿真中利用记录仿真流的溢出和中断统计,带式运输和矿仓的作用得以评估。通过仿真发现,增加矿仓可以使运输系统的生产能力提高13.2%[1]。文献[2]利用计算机仿真方法来分析矿仓如何提高系统的有效度,并且给出了计算地下煤矿中软连接带式运输系统有效度的方法。文献[3]用随机过程和线性规划方法对矿仓系统的可靠性问题进行建模和分析。文献[4]利用排队论研究矿仓的合理容量。文献[5]针对矿仓在转载过程中不同于一般贮仓的特殊使用条件,提出了确定装料过程及振动放料过程贮料压力的经验公式,为矿仓的结构优化设计奠定基础。文献[6]通过分析得出,马钢港务原料总厂矿仓堵塞严重,影响生产作业,提出通过安全隐患整治及技术改造,解决了生产实际问题。类似的还有文献[7-16]等。这些文献在研究工业带式运输系统中矿仓的控制和动态优化时,要么以经济性为目标,要么以可靠性为目标。因为经济性与可靠性的量度量纲不同,不容易放在一起统一进行定量分析,所以很少有文献在研究采矿工程中带式连续运输系统中矿仓的控制和动态优化时,将可靠性与经济性动态优化集成在一起考虑。基于这一点,本研究提出了一种新的采矿工程中带式连续运输矿仓容量的可靠性与经济性动态优化集成控制方法。
1 矿仓对带式连续运输系统可靠性和生产效益影响分析
带有矿仓的采矿工程中带式连续运输系统的示意图如图1所示。

矿仓容量对整个采矿工程中带式连续运输系统可靠性和生产效率的影响可讨论如下:
(1)当仓前环节1出现故障时,仓后环节2可继续运出仓中的存料,运出存料的最大值为矿仓的设计容量,设为Q。经过一定时间,如仓前环节1仍处于故障中,矿仓会放空,整个采矿工程中带式连续运输系统将会停止工作。
(2)当仓后环节2出现故障时,仓前环节1可继续往仓中运进物料,运进物料的最大值也为矿仓的设计容量,即为Q。经过一定时间,如仓后环节2仍处于故障中,会出现满仓,整个采矿工程中带式连续运输系统将会停止工作。
2 矿仓与其前后环节动态故障规律分析
采矿工程中带式连续运输系统中矿仓容量通常与矿仓的输入物流量和输出物流量,仓前环节1、仓后环节2的故障时间等随机变量有关,研究这些随机变量的概率规律时,以往文献常常用指数分布和正态分布进行拟合检验。指数分布虽然可以近似地作为某些高可靠性的复杂部件、机器或系统的失效分布模型,但是指数分布具有缺乏“记忆”的特性。所谓缺乏“记忆”,是指某种产品或零件经过一段时间t0的工作后,仍然如同新的产品一样,不影响以后的工作寿命值,或者说,经过一段时间t0的工作之后,该产品的寿命分布与原来还未工作时的寿命分布相同。显然,指数分布的这种特性,与采矿工程中带式连续运输系统中大量含机械零件环节的疲劳、磨损、腐蚀、蠕变等损伤过程相矛盾。相对指数分布,威布尔分布有更强的适用性,在很多情况下,同样故障数据的拟合处理可以通过指数分布或正态分布的检验,可能也会通过威布尔分布检验。而威布尔分布在某些情况下更能够准确反映部件或系统的实际特征,因此更适宜用作采矿工程中带式连续运输系统故障数据的处理和动态可靠性分析。指数分布和正态分布可看作威布尔分布的阶段特例,如在新开发的三参数威布尔分布中,β=1左右时近似指数分布,在β=3左右时近似正态分布。
鉴于上述原因,本研究在对采矿工程中带式连续运输系统中矿仓容量进行可靠性与经济性动态优化集成控制研究时,选择适用性更强的3参数威布尔分布作为工具。假定矿仓的输入物流量和输出物流量均为负指数分布,仓前环节1、仓后环节2的故障时间也属于3参数威布尔分布。
3 3参数威布尔分布
3参数威布尔分布较指数分布复杂,其概率密度函数
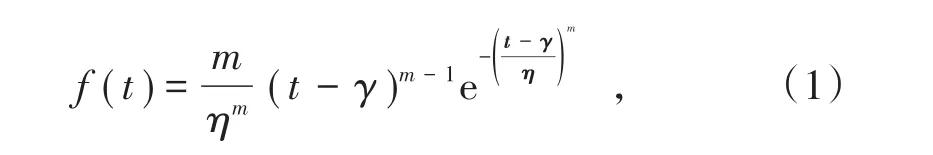
分布函数

可靠度函数
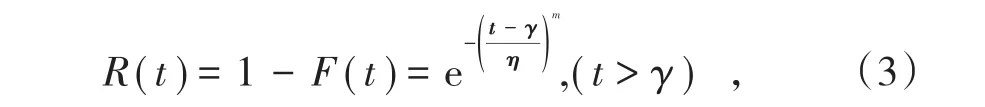
式中,m为形状参数,决定分布密度曲线的基本形状;γ为起始参数,决定分布密度曲线的起始位置,表示系统失效是从γ之后开始的,在时刻γ之前完全可靠;η为尺度参数,仅起到放大缩小标尺的作用,不影响分布的形状。
3参数威布尔分布的均值:

式中,Gamma函数
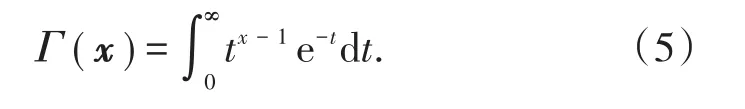
4 可靠性与经济性动态优化集成考虑方法
当仓前环节1出现故障时,仓后环节2可继续运出仓中的存料,运出存料的最大值为矿仓的设计容量Q。这儿仅考虑矿仓设计容量对整个采矿工程中带式连续运输系统有影响的情况,当仓前环节1处于故障的持续时间t1满足式(6)时,空仓会出现,然后整个采矿工程中带式连续运输系统将会停止工作。

式中,t1为仓前环节1处于故障的持续时间,min;Q为矿仓的设计容量,t;t01为仓前环节1处于故障持续时间的临界值,min;E2为矿仓输出物料运输速率的数学期望(代表一般情况),t/min;。
3参数威布尔分布的可靠度函数表达式为

故1 a中矿仓空仓出现的次数可按下式计算:

式中,n1为1 a中仓前环节1处于故障的次数;参数m1,η1,γ1可以通过采集仓前系统的故障时间,利用统计学的方法得出。
式(8)利用3参数威布尔分布的可靠度函数(7)推导得出,反映了矿仓系统的可靠性特征。
空仓出现1次所造成的损失可表示为:
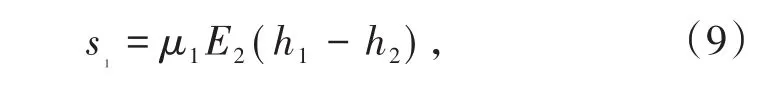
式中,h1为每吨物料的售价,元/t;h2为每吨物料的成本,元/t;μ1为仓前环节1各次故障时间的均值,min/次,其计算公式为

式(9)反映了矿仓系统的经济性特征。
1 a中空仓所造成的损失为

式(11)利用反映系统可靠性特性的式(8)和反映系统经济性特性的式(9)合成推导而来,因而体现了矿仓系统的可靠性与经济性动态优化的集成。
当仓后环节2出现故障时,仓前环节1可继续运物料进仓中,运进物料的最大值为矿仓的设计容量Q。同样仅考虑矿仓设计容量对整个采矿工程中带式连续运输系统有影响的情况,当仓后环节2处于故障的持续时间t2满足式(12)时,满仓会出现,整个采矿工程中带式连续运输系统将会停止工作。

式中,t2为仓后环节2处于故障的持续时间,min;Q为矿仓的设计容量,t;t02为仓后环节2处于故障持续时间的临界值,min;E1为矿仓输入物流速率的数学期望(代表一般情况),t/min。
利用式(7),1 a中矿仓满仓出现的次数可按下式计算:

式中,n2为1 a中仓后环节2处于故障的次数;参数m2,η2,γ2可以通过采集仓后系统的故障时间,利用统计学的方法得出。
式(13)利用3参数威布尔分布的可靠度函数(7)推导得出,反映了矿仓系统的可靠性特征。
满仓出现1次所造成的损失可表示为:
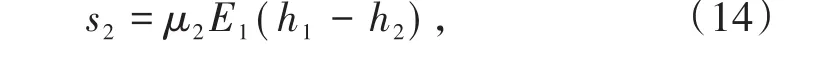
式中,μ2为仓后环节2各次故障时间的均值,min/次,其计算公式为
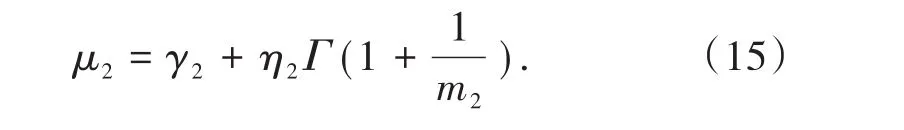
式(14)反映了矿仓系统的经济性特性。
1 a中满仓所造成的损失为

式(16)利用反映系统可靠性特性的式(13)和反映系统经济性特性的式(14)合成推导而来,因而体现了矿仓系统的可靠性与经济性动态优化的集成。
矿仓的建造需一定的费用,将这些费用分配到1 a中,则每年的花费为

式中,b1为矿仓每吨的建造费,元/t;T为矿仓的服务年限,a;b2为矿仓每吨的维护费,元/t。
5 建立可靠性与经济性动态优化集成控制模型
通过上述分析,为得到矿仓设计仓容的最优值,可以建立以下规划模型:

式(18)由反映矿仓系统可靠性与经济性动态优化集成的式(11)、式(16)和反映系统经济性特性式(17)推导得出,因而也反映矿仓系统可靠性与经济性动态优化的集成考虑。
按照极值理论,矿仓设计仓容达到最优值的条件为:

从式(20)可看出,在大系统范围内设计矿仓容量时,应考虑的因素包括:矿仓仓前环节1物料运输速率E1、仓后环节2物料运输速率E2、仓前环节1和仓后环节2的故障规律参数(如n1,n2,μ1,μ2,m1,γ1,η1,m2,γ2,η2)、矿仓每吨容量的建造费b1和维护费b2,每吨物料的售价h1和成本h2。
方程(20)只有1个未知数Q,其近似值求解步骤:
Step1任选一个初值Q1(Q1值作为迭代的开始,对最后近似值影响不大),令k=1。
Step2将Qk值代入式(20)中,求解f(Q1)和f(Q1)的一阶导数f'(Q1)。
Step3利用下面递推公式求解Qk+1

Step4是否满足下列2个条件之一:

其中,ε1、ε2为任意小正数,是则停止计算,计算出的Qk+1即为所求的最优矿仓容量;否则转Step2。
6 结 论
矿仓在采矿工程带式连续运输系统中经常出现,其容量大小的设计一般依照经验,本研究通过详细分析矿仓系统的动态变化,将可靠性与经济性动态优化集成,建立了综合考虑的规划模型,为复杂采矿工程中带式连续运输系统矿仓容量的设计提供了科学依据。本研究提出的方法充分考虑了矿仓容量对整个大运输系统可靠性和生产效率的影响,从而可实现大系统范围内矿仓容量的可靠性和经济性的整体优化。
