锥形外表面涂料喷雾流场特性研究
2021-01-18陈文卓陈诗明杨桂春
周 爽 陈 雁 陈文卓 陈诗明 杨桂春
(1.陆军勤务学院油料系;2.中国人民解放军62217部队)
石化工业中存在大量锥形外表面,如管道大小头、锥形罐及锥形管等。 锥形外表面直接影响喷雾流场, 喷雾流场又直接影响涂层的均匀性、光洁度及涂着效率等。 研究锥形外表面涂料喷雾流场特性对于揭示喷涂成膜规律、优化喷涂轨迹及提高喷涂质量等具有重要意义[1]。
计算流体力学是探究喷涂成膜机理的有效方法[2,3]。 其方法包括欧拉-拉格朗日法[4]和欧拉-欧拉法[5]。欧拉-拉格朗日法能够详细地对单个涂料液滴的运动进行跟踪和计算,得到液滴运动轨迹、液滴和空气两相的速度、压力等信息,但计算量大。 欧拉-欧拉法因气液两相采用同一套数值方法,计算量较小,并能够较好地描述大量液滴在气流中的湍流混合过程,是研究涂料喷雾流场的有效手段。
笔者采用欧拉-欧拉法建立由喷雾流场模型和撞击粘附模型构成的喷涂成膜模型,通过仿真分析揭示锥形外表面涂料喷雾流场特性,并用实验验证其正确性。
1 喷涂模型
1.1 喷雾流场模型
欧拉-欧拉法将涂料液滴相视为与空气相类似的连续流体,喷雾流场模型用统一的控制方程表示(当下标s为a、p时,分别表示空气相和涂料液滴相)。 模拟喷涂过程中环境温度保持不变,可忽略两相流动中的传热现象, 不建立能量守恒方程,故只建立质量守恒方程和动量守恒方程:

式中 Fd,s——曳力,N/m3;
g——重力加速度,m/s2;
p——相共同作用的压力,N/m2;
vs—— s相的速度,m/s;
ρs—— s相的密度,kg/m3;
τs—— s相的粘性应力,N/m2。
喷雾流场中的涂料液滴可视为理想球形,而空气与液滴的密度比远小于1, 所以曳力Fd,s采用Schiller-Naumann曳力模型进行计算,空气相对液滴相的曳力为:

其中,曳力系数CD取值0.44。
由于喷涂锥形面时近壁区域的湍流发展不够充分,采用标准壁面函数配合标准k-ε模型来封闭动量方程。 引入标准k-ε模型包含湍流动能k和湍流动能耗散率ε的输送方程为:
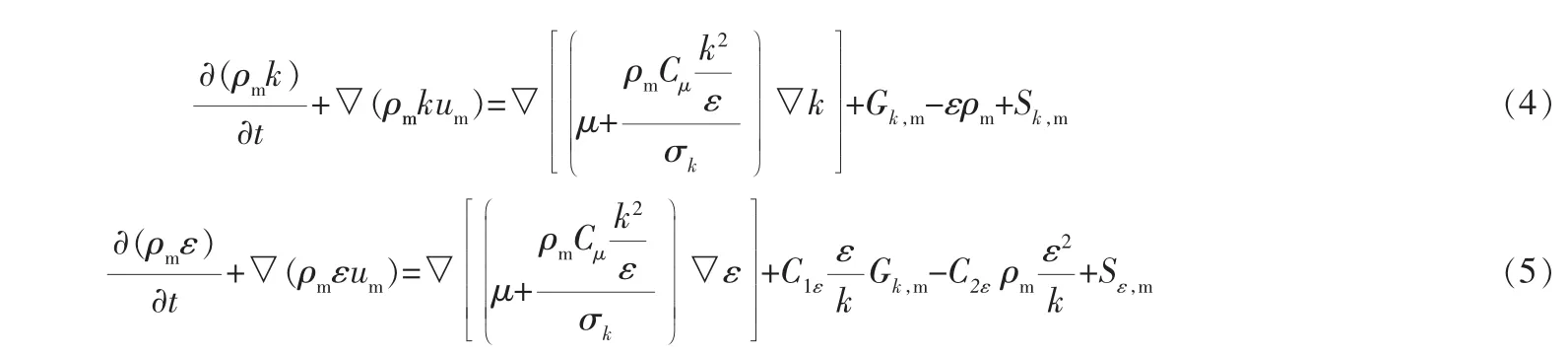
式中 k2——湍流速度尺度;
Gk,m——平均速度梯度产生的湍流动能项,kg/(m·s3);
um——混合相速度,m/s;
μ——混合相动力粘度,N·s/m2;
ρm——混合相密度,kg/m3。
Cμ、C1ε、C2ε、σk和σε为常数, 分别取值0.09、1.44、1.92、1.0和1.3;Sk,m和Sε,m为两相间的湍流作用附加项。
1.2 撞击粘附模型
喷涂的涂料液滴到达壁面附近,取某一控制体建立守恒方程,对比撞击前后情况,涂料液滴的质量和动量都发生变化,将涂料液滴相的质量和动量作为源项加入到壁面液膜守恒方程中,分别建立液膜的质量守恒方程和动量守恒方程,通过连续方程组的求解得出液膜的厚度。
质量源项为:

式中 A——壁面面积,m2;
Vpn——涂料液滴相沿壁面的法向速度,m/s;
αp——涂料液滴相体积分数;
ρp——涂料液滴相密度,kg/m3。
质量源项加入后的质量守恒方程:

式中 h——壁膜的高度,m;
Vl——平均液膜速度,m/s;
ρl——壁膜密度,kg/m3。
动量源项为:

式中 Vp——涂料液滴相的速度矢量,m/s。
动量源项加入后的动量守恒方程:

其中,方程左侧两项分别表示相瞬态变化和对流输送, 方程右侧依次表示空气流动压力、液膜表面张力和垂直于壁面的重力分量共同作用,重力在平行液膜方向上的作用,空气与液膜交界面的粘性剪切力作用, 液膜与壁面的粘滞力作用,形成液膜的动量源作用。
2 数值模拟计算
2.1 模型与喷涂方式
计算用外混式雾化喷枪空气帽简化模型如图1a所示,涂料入口孔孔径1.1mm,中心雾化孔外径和内径分别为2.0、1.6mm,4个辅助雾化孔孔径为0.5mm,扇面压力孔孔径为0.8mm。 坐标系如图1b、c所示, 原点位于涂料入口孔的中心,z轴沿空气帽中心轴线朝向喷涂方向,x轴为辅助雾化孔中心连线方向,y轴在与扇面压力孔中心所在平面垂直的方向上,同时与x轴保持垂直。
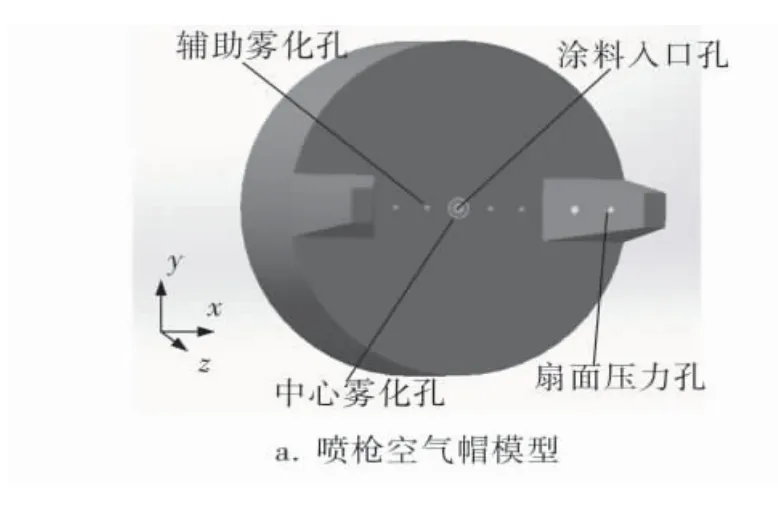
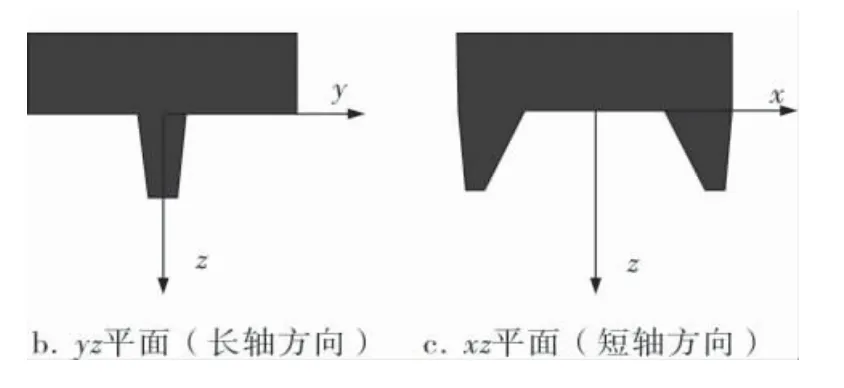
图1 三维空气帽模型及坐标系
采用60°圆锥角锥形外表面与半径180mm圆弧面进行静态喷涂对比研究。 喷涂锥形外表面的喷锥底心曲率半径为180mm。 在圆锥角为α的圆锥外表面上(图2),喷锥底心的曲率半径为R1,则喷锥底心所在圆锥截面圆半径R为:


图2 锥形外表面喷涂位置示意图
在锥形面和圆弧面上的喷涂方式有沿母线喷涂和周向喷涂两种,如图3所示。 沿母线喷涂是指喷涂时喷锥底心在母线上运动;周向喷涂是指喷涂时喷锥底心在圆锥或圆柱的截面圆上运动。喷涂时喷枪轴线方向与锥形面和圆弧面的法线方向相同。

图3 外表面喷涂方式
2.2 计算域与参数设置
参数设置分别为: 喷涂顶角60°、 半径290mm、与顶点距离580mm的锥形外表面,半径180mm、长300mm的圆弧外表面。 二者的计算域和网格划分分别如图4所示。 图4中,蓝色网格区域为压力出口边界, 灰色区域为待喷涂目标壁面,红色区域为喷枪,采用多面体网格划分流体计算域。

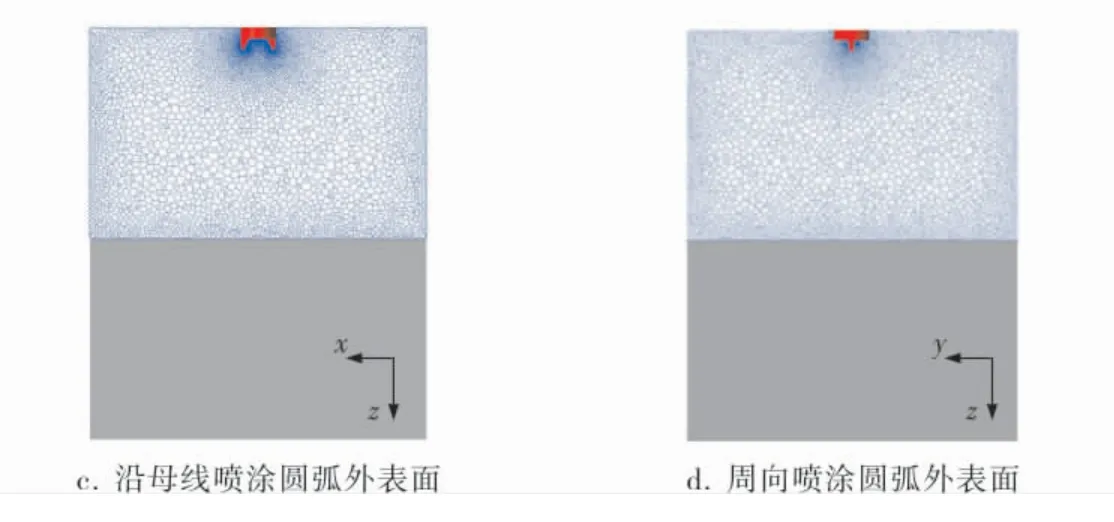
图4 流体计算域和网格划分
喷雾流场为两相混合流场,第1相为空气,第2相为涂料。 操作环境为1标准大气压,重力加速度为9.81m/s2。 中心雾化孔、辅助雾化孔与扇面压力孔设为压力进口, 空气压力分别为120、100、110kPa。 涂料入口孔设为质量流量进口,涂料的密度1 200kg/m3,粘度0.096 86kg/(m·s),表面张力系数0.028 719 4N/m,质量流量0.001 32kg/s。喷涂距离为180mm。
采用相耦合SIMPLE算法求解二阶迎风格式离散后的代数方程组,迭代时间步长设置为1×10-4s,迭代时间0.5s。 迭代500次后计算得到的残差值为1×10-4。
3 计算结果与分析
3.1 喷雾雾形与速度分布
通过仿真得到喷涂圆弧和圆锥外表面的喷雾流场,发现喷锥都呈椭圆锥形。 其原因是受到空气帽两侧扇面压力孔气流的冲击,喷雾锥在xz平面内被压缩,在yz平面内扩展(图5)。这两种形面对长轴和短轴方向的喷雾流场的影响是类似的,且喷雾流场在喷锥长轴(yz平面)比在短轴(xz平面)上的尺度大很多,喷锥长轴上的喷雾流场对最终涂膜厚度分布的影响比喷锥短轴大得多,所以仅针对喷锥长轴方向的喷雾流场进行分析。
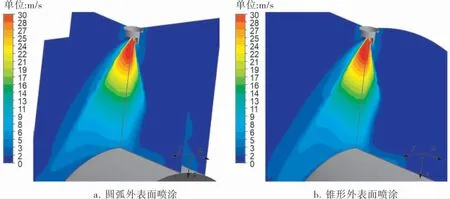
图5 沿母线方向上喷雾幅度对比
在圆弧与圆锥外表面的两种喷涂方式中,长轴(yz平面)方向的液滴速度云图如图6所示。 其中,yz平面的喷锥雾形剖面近似等腰三角形,z轴上,液滴速度随z的增大而降低;在z轴相同距离处,中心处液滴速度高于喷锥两侧的速度。
3.2 喷雾流场横向扩展
喷锥角度是指喷雾流场yz平面上的两条喷锥轮廓线的夹角。 它表示喷锥雾形的最大横向扩展程度, 确定喷涂形成涂膜的范围。 喷锥如图7所示。
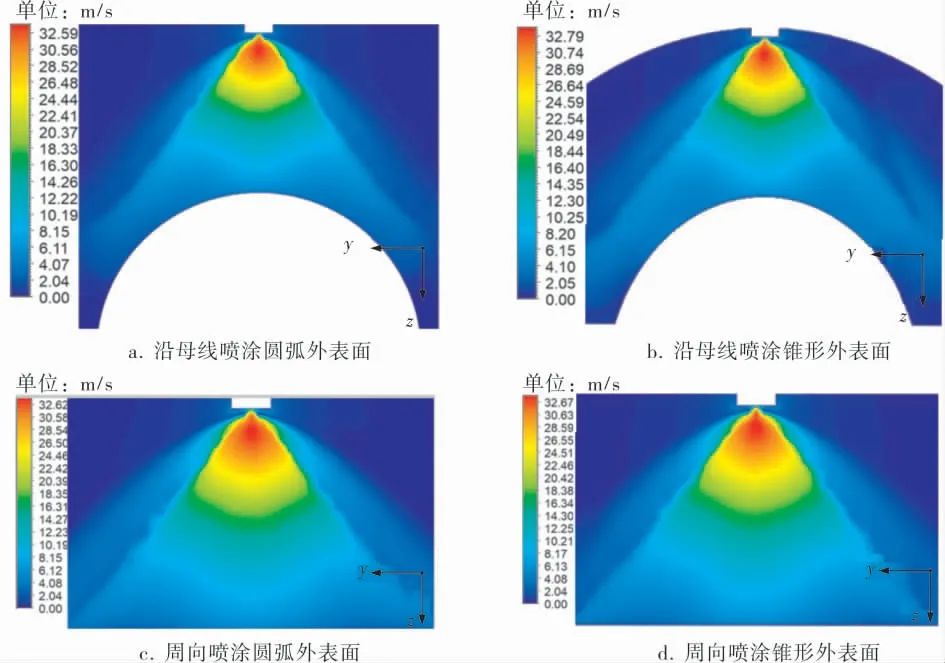
图6 外表面喷涂时长轴方向的液滴速度云图
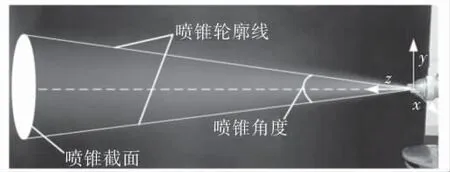
图7 喷锥示意图
根据射流理论,射流的速度半值宽y(U50%)可以表示射流的横向拓展程度。yz平面内,速度半值宽是速度为中心线(z轴)上速度值一半时的y坐标值。 两种喷涂方式下锥形面和圆弧面的yz平面液相在y方向的横向扩展程度与z坐标值关系如图8所示。

图8 不同喷涂方式的喷雾横向拓展程度
速度半值宽y(U50%)与z坐标可近似为线性关系。 拟合出不同喷涂方式下的喷锥角度,其中沿母线喷涂时, 圆弧外表面的喷锥角度为77.3°,锥形外表面的为77.5°;周向喷涂时,圆弧外表面的喷锥角度为77.4°,锥形外表面的为78.6°。
由于湍动能的作用,喷雾横向拓展程度存在微小的波动,导致喷锥角度的不同,但在轴向距离0.01~0.14m范围内(即远离壁面的范围内),是锥形外表面还是圆弧外表面对喷雾流场几乎没有影响。
3.3 近壁面喷雾流场
由式(6)~(9)可知,影响涂料液滴成膜的主要参数是壁面处液滴相的法向速度和切向速度,所以必须研究在两种形面上法向速度和切向速度的分布。
为描述喷雾液滴法向速度和切向速度沿壁面的分布, 定义沿母线喷涂形面的坐标如图9所示。 图9中,z1为远离壁面的法线方向,y1为平行于壁面的方向,O1为喷枪轴线与壁面的交点。 沿母线喷涂时, 喷枪yz平面与圆弧外表面相交形成一个圆线(图9a中的黑线),与60°圆锥角锥形外表面相交形成一个椭圆线(图9a中的绿线)。 周向喷涂时, 喷枪yz平面与圆弧外表面和锥形外表面的交线均是直线。
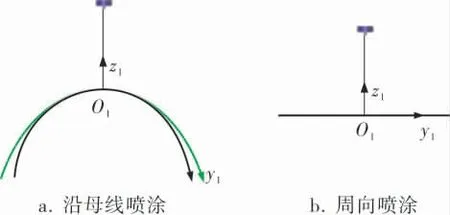
图9 喷涂壁面坐标定义
利用距离壁面10mm处的法线速度,研究近壁面法向速度分布;利用距离壁面10mm内的最大切向速度,研究近壁面的切向速度。由于喷雾流场的对称性, 仅针对近壁面处远离交点方向的喷雾流场进行研究。不同方式喷涂圆弧面和锥形面时,近壁面液滴的法向速度沿壁面的分布如图10所示,最大切向速度沿壁面的分布如图11所示。

图10 液滴法向速度沿壁面的分布
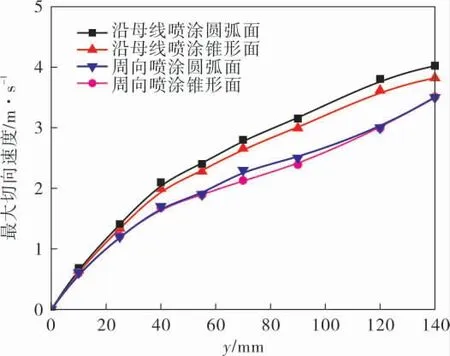
图11 液滴最大切向速度沿壁面的分布
由图10、11可知,周向喷涂时,两种形面的近壁面法向速度几乎相同,且高于沿母线喷涂的近壁面法向速度; 两种形面的近壁面最大切向速度几乎相同, 且分别低于沿母线喷涂的近壁面最大切向速度。沿母线喷涂时,锥形面的近壁面法向速度高于圆弧面,近壁面最大切向速度低于圆弧面。
不同喷涂方式下圆弧和锥形外表面近壁面处液滴速度矢量图(图12)对比可以解释上述现象。 沿母线喷涂圆弧面或圆锥面时,由于形面因素(图13),液滴速度矢量与壁面法线的角度高于周向喷涂,使得液滴撞击壁面的法向速度低于周向喷涂, 沿壁面的最大切向速度高于周向喷涂。沿母线喷涂圆弧面时,液滴速度矢量与壁面法线的角度大于沿母线喷涂锥形面,所以沿母线喷涂锥形面时的近壁面法向速度高于沿母线喷涂圆弧面,且沿母线喷涂锥形面时的近壁面最大切向速度低于沿母线喷涂圆弧面。
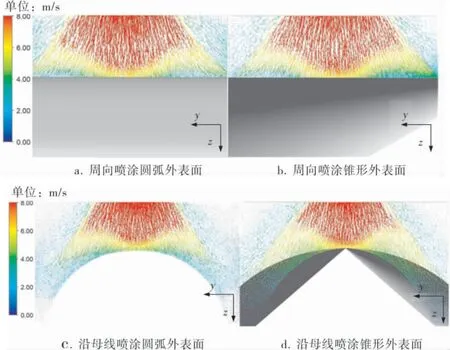
图12 近壁面液滴速度矢量图
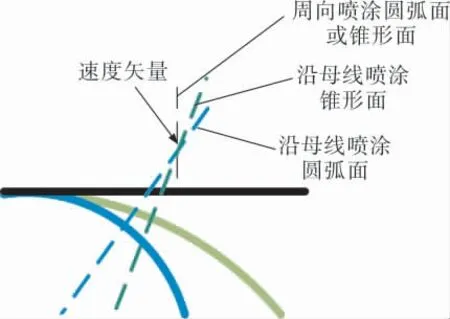
图13 同一矢量与不同形面法线的角度
4 实验验证
为验证仿真结果,按仿真内容设置并进行两组实验。 喷涂时使用秒表测量并记下喷涂时间。喷涂完成后到形成完全干漆膜过程中不压碰漆膜。 在干漆膜中心建立坐标轴,使用涂层测厚仪测量, 每隔10mm记录一个点的坐标值和漆膜厚度。 干膜厚度除以喷涂时间得到漆膜厚度增长速率。
仿真漆膜形状与实验漆膜形状如图14a、b所示,仿真漆膜形状与实验大体一致。 仿真与实验的漆膜厚度增长速率(干膜厚度与喷涂时间的比值)对比如图15所示。 仿真结果和实验结果整体比较吻合,误差主要在于实验漆膜中心处速率低于仿真,两侧略高于仿真。 这是因为实验中形成的湿膜在干燥固化过程中,有部分组分挥发,在重力和涂料表面张力的作用下漆膜会向四周微弱运动。
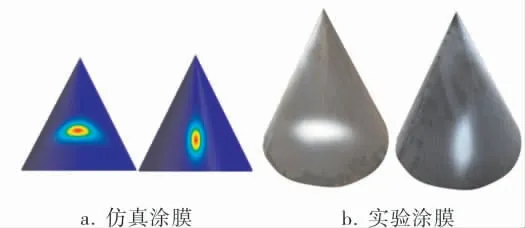
图14 仿真与实验漆膜形状

图15 漆膜厚度增长速率
仿真与实验的漆膜形状大体一致,漆膜厚度增长速率吻合良好,表明建立的喷涂成膜模型适用于锥形外表面涂料喷雾流场特性研究。
5 结论
5.1 不同喷涂方式下,锥形外表面与圆弧外表面上的喷雾形状相似,都呈椭圆锥状;在远离壁面区域,两形面对喷雾流场几乎没有影响。
5.2 在靠近锥形面壁面区域,周向喷涂时喷雾法向速度高于沿母线喷涂,且最大切向速度低于沿母线喷涂,法向速度和最大切向速度与圆弧外表面几乎相同;沿母线喷涂时,锥形外表面的喷雾法向速度高于圆弧外表面,且最大切向速度低于圆弧外表面。
5.3 仿真与实验的漆膜形状大体一致,漆膜厚度增长速率吻合良好,表明建立的喷涂成膜模型适用于锥形外表面涂料喷雾流场特性研究。
