弯头裂纹缺陷对超声导波回波幅值的影响研究

唐登超 邓建强 丁 菊 朱旭晨

（1.西安交通大学化学工程与技术学院；2.上海市特种设备监督检验技术研究院）

管道运输具有安全性高、连续性强、成本低及效益好等优点，在石油化工产业中发挥着重要作用。 弯头作为管道系统中的重要部件，处于流体的主要冲刷部位，在役期间易受复杂工况的影响，轻则受腐蚀产生裂纹，重则发生泄漏，危及整个管道系统的结构安全。 对比各种传统无损检测，如漏磁、超声、涡流、射线及磁粉检测等，超声导波沿传播路径衰减小， 可沿构件传播几十米，超声导波在管的内外表面和中部都有质点的振动，声场遍及整个壁厚，既可检测构件内部缺陷，也可检测内外表面缺陷，因此超声导波检测实质上是检测了发射和接收两面间或者发射兼接收面与固定约束端面间传播路径上的整体信息。 对于弯头众多且结构比较复杂的管道结构来说，超声导波无损检测技术是一种简洁、高效且易于操作的无损检测技术。

超声导波是在波导结构中传播的超声波，在传播过程中不仅会受到结构尺寸的影响，还会受到频率的影响，导波的相速度大小随频率变化而变化的现象称为频散。 频散是材料本身的固有特性， 使得超声导波在传播过程中发生能量的衰减。 频散曲线指出了所有传播路径中的相长干涉区域， 同时描绘了具有传播能力的各种模态形式，主要有轴对称纵向L（0，m）模态、轴对称扭转T（0，m）模态和非轴对称弯曲F（n，m）模态3 种，其中n 表示目标模态的环向阶数，m 表示目标模态在管道中径向的振动形式。 弯曲F（n，m）模态超声导波由于本身激励方式复杂且耗散太快，模态不稳定，一般不常用于无损检测，轴对称纵向L（0，m）模态和轴对称扭转T（0，m）模态的加载方式相对简单，其中纵向L（0，2）模态导波和扭转T（0，1）模态导波传播速度快、模态稳定、频散现象小，是管道缺陷无损检测的理想模态。

在超声导波模态转换、频散曲线等理论研究方面，Lowe M J S 等分析总结了不同程度缺陷对导波的模态转换规律和缺陷反射规律， 开发出Disperse 商用软件， 可对各种规则物体计算其频散曲线，提高识别缺陷的精度，并用纵向L（0，2）模态导波验证了不同缺陷管道；研究了纵向L（0，2）和 扭 转T（0，1）两 种 激 励 模 态 与 缺 陷反 射 系 数 之 间 的 关 联，并 总 结 了 相 关 规 律［1，2］。Alleyne D N 等激励纵向模态导波对拥有不同半径的管道中的缺陷进行了分析，总结了不同方向上周向缺陷的反射系数与管道半径之间的关系［3］。 他得安等通过分析不同厚度和内径的管道的频散曲线，得出管道的内径和厚度之比与频散状态存在一定的关系［4］。

在超声导波激发设备 （如传感器和压电晶片）方面，李一博等研究了传感器数量和间距对于导波检测的影响，并以纵向L（0，2）模态导波为例研究频率对管道中缺陷检测灵敏度的影响和一次导波有效检测长度的区别［5］。 王悦民等研究激励频率和激发模式之间的联系，通过选取激励频率可以抑制相关干扰波的产生［6］。 Nishino H 等将压电晶片周期均匀布置在管道圆周，激发出扭转T（0，m）模态用于管道检测［7］。 Liu Z H 等开发的MPSA-MPT 阵列线圈可以增强扭转T（0，1）模态 的 信 号 强 度［8］，Nurmalia 等 采 用 电 磁 传 感 器 激励出扭转T（0，1）模态导波，通过改变管道上缺陷的形状来研究其模态转换现象［9］，Kim H W 等将磁致伸缩贴片线圈均匀布置在管道圆周，成功激发出扭转T（0，1）模态，实验验证了该方法具有识别管道中多个轴向裂纹位置的潜力［10］。

管道几何结构对超声导波具有影响。Verma B等采用纵向L（0，2）模态导波对不同的弯曲管道进行实验，研究总结了不同弯曲角度管道的透射率和模态转换规律，还研究了不同壁厚的弯曲管道对模态转换的影响［11］。 Ni J 等研究了不同弯曲状态下弯管的传播特性、 缺陷检测灵敏度等问题，并通过实验进行验证［12］。 何存富等通过使用L（0，2）模态导波对弯头上不同位置的缺陷进行模拟和实验检测，验证L（0，2）模态导波可以检测弯头处的缺陷［13］。 王秀彦等实验研究了不同中心曲率半径的90°弯管的透射系数， 总结出弯管中心曲率半径与透射系数之间的关系［14］。 王悦民等使用超声导波对多弯头的管道进行实验研究，发现磁致伸缩激励的超声导波可以检测管道缺陷，但弯管中的能量衰减呈指数下降［15］。

采用有限元方法模拟超声导波在管道中的传播、频散现象和模态转换方面，是一种有效、成熟的研究手段。 何存富等模拟了纵向L（0，m）模态和弯曲F（1，m ）模态导波在管道中的传播过程，观测到各个模态的频散现象，其中纵向L（0，2）模态导波频散现象最小，传播速度最快［16］。郑明方等使用ABAQUS 有限元模拟了纵向L（0，2）模态导波在环形缺陷圆管中的传播过程，发现在经过环形缺陷时超声导波由纵向L（0，2）模态转换成纵向L（0，1）模态［17］。 Demma A 等模拟了超声导波在弯头处的频散现象，并总结了不同模态导波在弯头处反射率与透射率的关系［18］。Nishino H 等模拟了纵向L（0，1）模态导波在不同弯曲角度的弯管中的传播现象，观测到在低频范围内，纵向L（0，1）模态经过弯头时会转换成弯曲F（1，1）模态，且幅值强度随着弯管弯曲角度的增加而增加［19］。

目前，超声导波无损检测技术在管道检测中的应用已经越来越成熟， 超声导波在检测范围、检测灵敏度方面有着极大的优势。 针对管道中的切槽、裂纹、孔、腐蚀及密集型坑洞等典型缺陷，基于不同模态超声导波进行了大量的实验研究，而裂纹缺陷结构参数作用于超声导波回波幅值的量化影响研究还不够。 鉴于模拟研究对实验研究的可视化表征方面发挥了积极作用，笔者采用数值模拟方法，通过改变弯管弯头处裂纹缺陷的位置和侧壁处缺陷的周向长度、轴向宽度和径向深度，探究对超声导波回波最大幅值相对值的影响规律，这对于利用超声导波快速分析裂纹缺陷的类型位置，判断是否进一步对设备管道进行健康诊断与监测有着参考价值。

1 模型建立

1.1 三维模型结构参数

弯管材料选用不锈钢材料，将弯管分为直管段和弯管段建立三维模型，管道模型参数如下：

弯管外径 60.30mm

弯管壁厚 3.91mm

弹性模量 217GPa

泊松比 0.286

密度 7 932kg/m3

弯头中心线曲率半径 100.00mm

如图1 所示， 在弯头处设置一个裂纹缺陷，通过改变缺陷轴向宽度a 和周向长度b 两个参数，能模拟出不同尺寸的周向裂纹缺陷，改变径向深度h，能模拟裂纹缺陷的局部减薄。笔者主要研究周向缺陷结构参数对纵向L（0，2）导波的影响。 笔者采用ABAQUS 有限元软件进行模拟，综合考虑计算速度和精度，采用四面体单元C3D10对管道进行网格划分，在裂纹缺陷区域进行网格加密，提高计算精度。

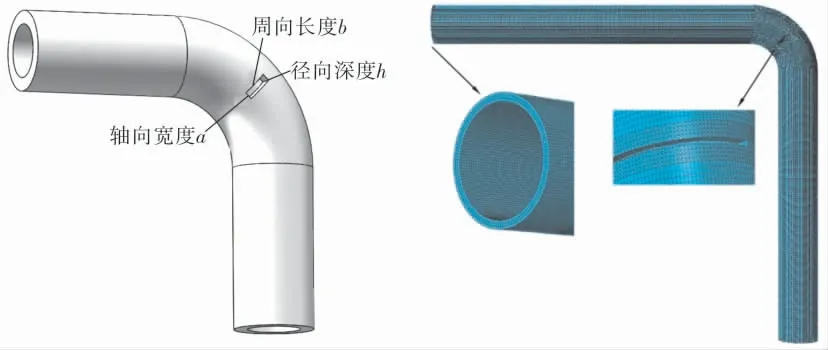
图1 裂纹缺陷的实体模型和网格模型

具体裂纹缺陷结构参数见表1。其中，在沿管道径向深度方向上设置的不同深度缺陷，分别代表由管道浅层表面直至贯穿整个壁厚的缺陷类型。 通过固定其中两个参数，改变第3 个参数的赋值，研究裂纹缺陷结构参数的改变对缺陷回波最大幅值相对值的影响，确定出超声导波经过弯头处不同参数缺陷的传播特性。

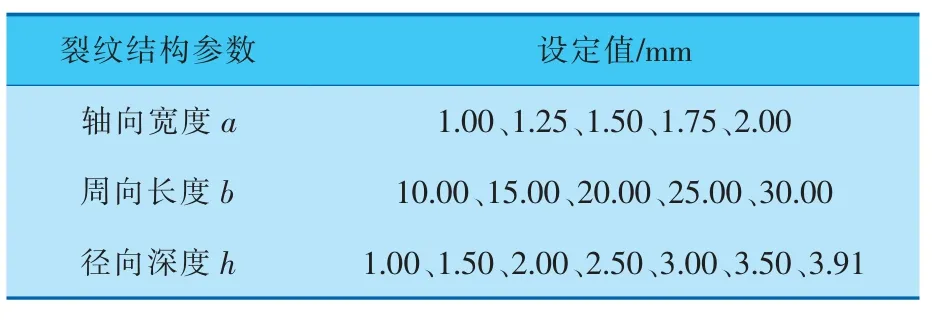
表1 管道裂纹缺陷结构参数

1.2 激励信号加载

如图2 所示， 将管道其中一个端面设为约束面，固定6 个自由度，另一端面设置为激励面，将激励面分为内、中、外3 个区域，其中的中间区域作为激励信号的加载区域，在激励信号的加载区域施加中心频率为70kHz、 周期数为5 的汉宁窗调制正弦超声导波信号，内部区域和外部区域作为激励信号的接收区域，用来接收裂纹缺陷回波和约束端面回波。

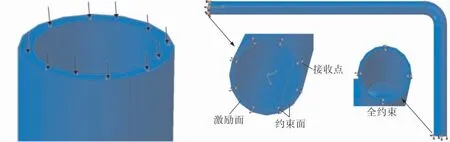
图2 纵向模态超声导波加载方式示意图

如在外径60.30mm、 壁厚3.91mm 弯管弯头侧壁处设置一个a=1.00mm、b=20.00mm 的周向裂纹缺陷，在端面激励一个超声导波信号，提取时域波形如图3 所示。 可以看出，时域波形中存在初始信号和明显的缺陷与端面回波，证明在弯头上的缺陷能够被检测出来。

2 模拟结果和分析

2.1 裂纹缺陷位置对超声导波回波最大幅值相对值的影响

图3 弯管周向裂纹缺陷检测的时域波形

超声导波在弯管中传播时，在弯头处会发生不同程度的衰减。 为了研究不同位置处的周向裂纹缺陷对导波检测的影响，以经过管道最外侧母线的中心面作为基准面， 分别每隔45°设置一个a=1.00mm、b=20.00mm 的周向裂纹缺陷， 分别表示为A、B、C、D、E（图4）。

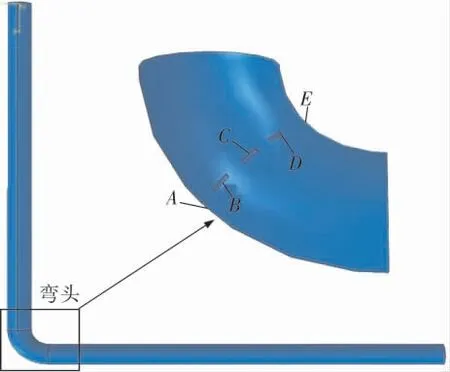
图4 裂纹缺陷位置分布示意图

为了提高计算精度，增加数据模型，分别设置3 种不同深度h （1.00、2.50、3.91mm） 进行分析，提取激励面接收区域接收的裂纹缺陷回波的最大幅值，与初始信号最大幅值相比，即进行归一化处理，其缺陷回波最大幅值相对值随缺陷位置角度与深度的变化关系如图5 所示。

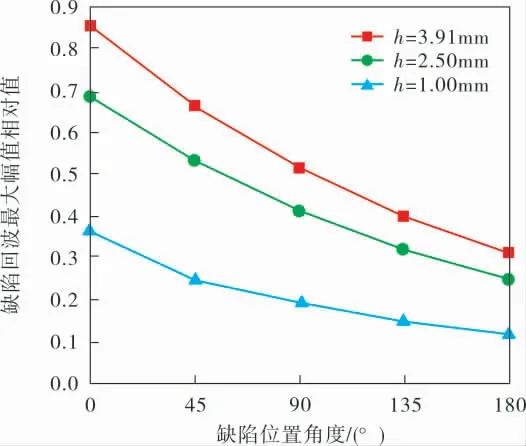
图5 缺陷回波最大幅值相对值随裂纹缺陷位置的变化

从图5 看出，裂纹缺陷在弯头外侧时缺陷回波最大幅值相对值明显高于内侧， 且逐步递减。表明裂纹缺陷在弯头内侧时，会出现比较大的能量耗散，不容易被检测，当裂纹缺陷出现在弯头外侧时，会有明显的缺陷回波，比较容易被检测。在弯头处由于管道几何结构的改变，导致超声导波反射、折射的路径发生了改变，纵向L（0，2）模态导波在弯头处发生了频散现象，在弯头内侧的缺陷不易被检测，外侧的缺陷比较容易被检测。

2.2 轴向宽度对L（0，2）导波缺陷回波最大幅值相对值的影响

考虑到缺陷位置对缺陷回波最大幅值相对值的影响， 在弯头90°侧壁C 处的缺陷回波最大幅值相对值适中，具有一定的代表性。 笔者研究侧壁C 处裂纹缺陷结构参数对回波最大幅值相对值的影响，提取不同裂纹的缺陷轴向宽度和径向深度， 获得各自的缺陷回波最大幅值相对值，如图6 所示。

图6 回波最大幅值相对值随轴向宽度的变化

从图6 可以看出，当缺陷的周向长度b 和径向深度h 固定时，不同的轴向宽度a 反射幅值起伏很小，说明对于纵向L（0，2）导波来说，轴向宽度a 的变化不是引起缺陷幅值变化的主要因素，纵向L（0，2）导波对于轴向宽度a 不敏感。表明对于沿管道轴向的缺陷（轴向宽度a 较小、周向长度b 较大）来说，纵向L（0，2）导波不易检测。

2.3 周向长度对L（0，2）导波缺陷回波最大幅值相对值的影响

由于纵向L（0，2）导波对于轴向宽度a 不敏感， 在弯头侧壁C 处， 固定缺陷轴向宽度a 为1.00mm 不会带来明显影响， 研究径向深度h 为1.00、2.50、3.91mm， 周向长度b 为10.00、15.00、20.00、25.00、30.00mm，提取不同缺陷周向长度和径向深度， 获得各自的缺陷回波最大幅值相对值，如图7 所示。

图7 回波最大幅值相对值随周向长度的变化

从图7 可以看出，对于管道浅层缺陷，即径向深度h 为1.00mm 时，纵向L（0，2）导波缺陷回波最大幅值相对值范围为0.15～0.29；对于管道中部缺陷，即径向深度h 为2.50mm 时，纵向L （0，2） 导波缺陷回波最大幅值相对值范围为0.24～0.52；对于贯穿整个管道壁厚的缺陷，即径向深度h 为3.91mm 时，纵向L（0，2）导波缺陷回波最大幅值相对值范围为0.31～0.64。 可以看出，缺陷回波最大幅值相对值对周向长度b 值的变化较为敏感，纵向L（0，2）导波可以检测沿管道周向的缺陷。 当缺陷轴向宽度a 和径向深度h 不变，b 值不断增大时， 缺陷回波幅值逐渐增大，但增长速率在逐渐减缓。

2.4 径向深度对L（0，2）导波回波最大幅值相对值的影响

在弯头侧壁C 处， 固定缺陷宽度为1.00mm，周向长度b 为10.00、20.00、30.00mm， 径向深度h分别为1.00、1.50、2.00、2.50、3.00、3.50、3.91mm，提取不同缺陷周向长度和径向深度， 获得各自的缺陷回波最大幅值相对值，如图8 所示。

从图8 可以看出，对比不同径向深度h 下的缺陷回波最大幅值相对值，纵向L（0，2）导波回波最大幅值相对值对缺陷深度h 的检测较为敏感，在周向长度b 为10.00mm 下，纵向L（0，2）导波缺陷回波最大幅值相对值范围为0.15～0.31；在周向长度b 为20.00mm 下，纵向L（0，2）导波缺陷回波最大幅值相对值范围为0.21～0.46；周向长度b 为30.00mm 下，纵向L（0，2）导波缺陷回波最大幅值相对值范围为0.28～0.62。 当缺陷轴向宽度a、周向长度b 固定不变时，缺陷深度h 增大，缺陷回波最大幅值相对值也明显增大，对比周向长度b，径向深度h 的影响更为明显。

图8 回波最大幅值相对值随径向深度的变化

3 结束语

笔者采用ABAQUS 软件模拟了超声导波在设置不同位置、不同结构参数的裂纹缺陷的弯头中的传播。 研究发现，超声导波在弯头处会出现频散现象，在弯头外侧缺陷回波最大幅值相对值比内侧的要高，而且逐步降低，表明在弯头内侧的裂纹缺陷比较难以检测，在弯头外侧的裂纹缺陷比较容易检测。对周向裂纹缺陷纵向L（0，2）导波来说，轴向宽度a 的改变对于纵向L（0，2）导波缺陷回波最大幅值相对值无显著影响，而周向长度b 和径向深度h 增大时，缺陷回波最大幅值相对值有明显增大，但对于周向长度b 的增长其变化速率有所减缓，相比较而言径向深度h 的影响更明显。 总的来说，缺陷在纵向L（0，2）导波振动方向上的特征长度越长，缺陷回波最大幅值相对值越大，缺陷越容易被检测。 研究结论对应用超声导波技术分析管道弯头纵向裂纹缺陷位置、参数敏感性以及是否采取进一步应对措施有着一定的参考价值。