基于等几何分析的参数多孔结构拓扑优化*

胡传丰, 任靖雯, 胡 慧, 蔺宏伟,2

(1. 浙江大学 数学科学学院, 杭州 310027;2. 浙江大学 计算机辅助设计与图形学国家重点实验室, 杭州 310058)

多孔结构是一种由大量孔洞组成的实体结构, 在自然界和人工制品中广泛存在, 如木材、骨骼、 珊瑚、 海绵等, 可长期承受较大的静态载荷和周期载荷. 与传统结构相比, 多孔结构具有质量轻、 比表面积大、 高渗透性、 高比强度等优点, 以及抗冲击性[1]、 阻尼增强[2]、 缺陷容忍性[3]等特性. 这些优良特性使其应用范围远超出单一功能材料, 因而广泛应用于组织工程、 轻量化设计及能量吸收等领域. 在组织工程领域, 高渗透性和高比表面积的多孔结构, 有助于建立一个适宜细胞附着、 迁移繁殖、 营养运输和新陈代谢等的生物微环境, 常被作为组织支架移植到人体组织缺损部位, 辅助组织修复再生[4-6]. 在轻量化设计领域, 由于多孔结构质量轻、 相对密度低, 因此利用多孔结构进行飞机机翼内部结构设计可有效降低机翼重量, 同时提高机翼抗弯刚度[7]. 在能量吸收领域, 由于多孔结构具有较大的压缩应变, 因此在受到外力冲击时, 可借助自身结构特性将动能转变为压缩能, 从而提高能量吸收能力[8]. 多孔结构的力学性能不仅与材料相关, 还与自身分布相关, 所以需对多孔结构进行结构分析和优化设计, 以提高其力学相关性能.

多孔结构的设计方法主要包括CAD(management software computer aided design)造型设计方法和隐式曲面造型设计方法, 其中CAD造型设计方法适用于设计简单规则的多孔结构. Cheah等[9]通过对多面体形状的研究, 设计了基于多面体的多孔单元库; Lal等[10]提出利用微球填充方法设计多孔支架. 隐式曲面造型以三向周期极小曲面(triply periodic minimal surface, TPMS)为研究热点. Yoo首先利用TPMS设计了多孔单元库, 同时提出了利用六面体单元映射的方法构建多孔结构[11]; 之后, Yoo通过对TPMS与实体进行求交并构建多孔结构, 求交运算中引入了距离场算法替代Boole操作, 极大减少了时间的消耗[4]，并利用径向基函数进行空间插值控制孔径大小分布, 构建了非均质多孔结构[5]. 为在多孔结构设计中充分利用多孔单元库, Yang等[12]利用Sigmoid函数和Gauss径向基函数以任意形状的过度边界融合两种不同类型的多孔单元, 生成了形状更复杂的多孔结构； Shi等[13]结合TPMS和Sigmoid函数从CT数据中重建多孔支架结构； Feng等[6]利用T样条函数表示几何模型, 通过分析TPMS的相关参数与多孔结构的孔隙率、 比表面积之间的关系, 设计了孔隙率、 比表面积可控的多孔结构； Savio等[14]基于TPMS提出了CAD环境下变厚度多孔结构几何建模的方法.

拓扑结构优化设计以力学原理和数学规划算法为基础, 通过优化方法改变工程结构的尺寸、 形状和拓扑, 在给定的设计域和约束条件下, 实现结构的最佳性能设计. 目前的拓扑优化方法主要分为4类: 变密度法[15-16]、 水平集法[17-18]、 拓扑导数法[19]和相场法[20]. 相比于传统有限元分析方法, 等几何分析方法紧密结合几何模型信息, 避免网格划分过程, 具有高阶连续性, 在保证几何精确性的同时, 可有效降低求解问题的自由度, 提高计算模拟精度和效率[21-22]. 由于拓扑优化中的变密度法具有直观的数学模型, 且实现简单、 计算高效, 因此, 可将等几何分析与变密度法融合发展形成基于变密度的等几何拓扑优化方法. Hassani等[23]提出了结合优化准则法的等几何拓扑优化方法, 并通过二维平面优化问题算例表明该方法可有效抑制棋盘格现象； Qian[24]提出了一种基于B样条函数的变密度框架下拓扑优化方法, 将密度分布引入B样条函数空间, 并将控制点对应的相对密度值作为优化变量进行拓扑优化； Liu等[25]利用变密度框架下的等几何拓扑优化方法分析了全局应力约束下的拓扑优化问题.

目前, 针对多孔单元的拓扑优化研究已取得许多成果[26-29], 对多孔结构的拓扑优化, 主要包含以下两类方法： 第一类方法[30-32]先优化设计域的材料密度分布, 然后根据密度分布将分析单元替换为对应材料密度下的多孔单元； 第二类方法[33-34]预先设计晶格和单元结构, 然后在一个单元内优化结构尺寸或壁厚. 这两类方法各有其优缺点, 例如： 第一类方法在结构层次上, 而不是在每个多孔单元中优化拓扑结构; 第二类方法在结构层和单元层上都得到了优化, 但仅适用于具有一定壁厚的规则多孔单元; 上述方法均为基于有限元分析的优化方法, 从而导致在处理相互连通的多孔单元时, 无法保证多孔单元密度分布或壁厚分布的连续性, 进而相邻多孔单元不能光滑连接. 特别地, Li等[26]基于TPMS提出了功能梯度周期曲面, 构建多孔单元结构与密度建立映射关系, 利用有限元分析方法求解柔顺度和热传导问题, 寻找最优的单元密度分布, 最后对单元密度进行空间插值获得节点对应密度值, 并生成功能梯度多孔结构. 本文提出的变密度框架下多孔结构等几何拓扑优化方法可有效结合上述两类方法的优势, 通过TPMS多孔单元特征参数改变单元壁厚, 同时建立与材料相对密度间的映射关系, 以多孔单元特征参数作为优化变量进行拓扑优化, 保证优化构建的多孔结构中多孔单元光滑连接.

本文利用TPMS设计参数多孔单元, 并分析多孔单元特征参数与材料分布间的关系, 再利用变密度框架下的等几何拓扑优化模型对多孔单元特征参数分布进行结构分析与优化, 以实现最佳的多孔单元特征参数分布, 提高多孔结构的力学性能. 相比基于传统有限元分析的结构优化, 等几何分析的物理模型和多孔单元特征参数采用B样条表示, 提高了仿真计算的精度, 同时多孔结构中多孔单元个数可调控, 无需与分析单元数保持一致, 且多孔结构中多孔单元间连接的连续性得到了保证. 本文方法主要有以下创新点： 1) 提出了基于等几何分析的参数多孔结构拓扑优化方法; 2) 多孔结构中多孔单元个数可调控; 3) 多孔结构中多孔单元间光滑连接.

1 预备知识

1.1 B样条

p次B样条曲线定义[35]为

(1)

其中{Pi}是控制点，Ni,p(u)是定义在节点向量U=(u0,u1,…,um+p+1)上的p次B样条基函数, 且满足u0≤u1≤…≤um+p+1. B样条基函数为

(2)

由此延伸定义出B样条曲面和B样条体, 分别为

(3)

(4)

特别地, 由于本文研究薄板多孔结构优化问题, 实际薄板以B样条曲面形式表示, 但针对平面应力问题, 薄板以二维B样条曲面表示.

1.2 三向周期极小曲面

TPMS是在欧氏空间中沿3个独立方向周期性无限延伸的隐式曲面, 具有平均曲率为零的特点, 并将空间平滑而连续地一分为二, 产生连通性优异的孔结构, 是多孔结构设计领域中一种较好的设计工具. 由于TPMS参数表达形式相对复杂, 因此通常采用Fourier级数定义的周期曲面对其逼近[36]:

(5)

其中Ak为振幅,hk为倒空间的格矢量,r为空间位置矢量,λk为波长,Pk为相位,C为等值面阈值常数. 表1列出了P,D,G,IWP 4种类型TPMS的表达式, 其中阈值C的有效范围确保TPMS连通.αu,αv,αw表示曲面在空间3个方向上的周期. 特别地, 相比于其他类型的TPMS, 这4种曲面具有更大的表面积, 在多孔结构设计中应用广泛[37]. 此外, 本文利用移动四面体方法[38]提取TPMS, 并构建多孔结构, 如图1所示, 均为一个完整周期内的曲面.

表1 TPMS三角函数表达式Table 1 Trigonometric function expression of TPMS

图1 4类TPMSFig.1 Four types of TPMS

1.3 多孔单元

本文基于一个完整周期内4种类型TPMS(图1)设计了如图2所示的4种类型多孔单元.

图2 4类TPMS多孔单元Fig.2 Four types of TPMS porous elements

在多孔结构拓扑优化设计中, 定义C值为多孔单元的特征参数, 用于调控多孔单元孔径的大小以及多孔单元内材料的相对密度. 通过数据统计与分析, 发现4种多孔单元的特征参数C与相对密度ρ间存在如图3所示的关系. 数据拟合结果表明, 在一定误差范围内, 特征参数C与材料相对密度ρ存在如下关系：

图3 多孔单元特征参数C与材料相对密度ρ的关系Fig.3 Relationship between characteristic parameter C of porous element and relative density ρ of material

ρ=k1C+k2.

(6)

表2列出了不同多孔单元对应的系数k1和k2.

表2 多孔单元特征参数C与材料相对密度ρ的函数系数Table 2 Function coefficients of characteristic parameter C of porous element and relative density ρ of material

2 基于等几何分析的设计参数化

等几何分析是一种新型的数值计算方法, 其将工程结构的几何表示、 分析及拓扑优化过程紧密结合. 相比于传统有限元分析方法, 等几何分析方法具有几何精确性和单元间高阶连续性的优点, 提高了结构分析的精确性和可信性. 结合等几何分析的拓扑优化方法, 可有效提高结构分析和拓扑优化的效率.

2.1 等几何结构分析

等几何分析以等参思想为基础, 利用几何模型的样条基函数和控制点替代有限元分析中的单元形函数和节点. 图4为双线性(p=q=1)和双二次(p=q=2)等几何单元组成的等几何分析网格.

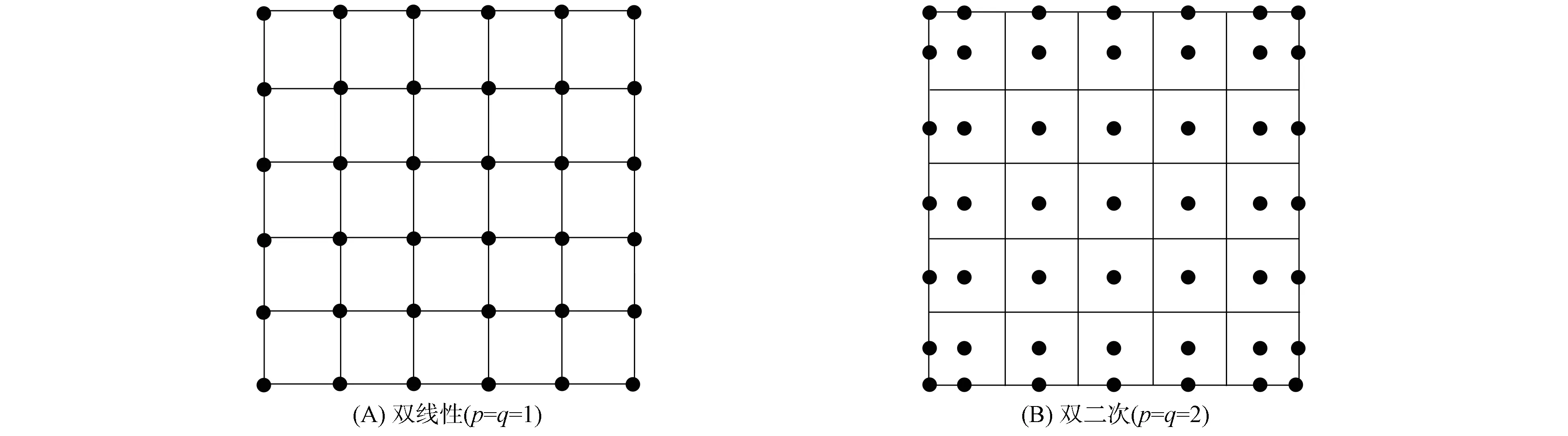
图4 等几何分析网格Fig.4 Iso-geometric analysis grid

进行结构分析时, 位移场表示为

(7)

其中,Ni,p(u),Nj,q(v)为式(2)中的B样条基函数，Uij为控制点处的位移系数. 本文利用等几何方法求解平面应力问题, 每个控制点处对应两个方向上的位移量Ux,Uy.

线弹性连续体的静力平衡方程可表示为

KU=F,

(8)

其中K为整体刚度矩阵，U为控制点处位移向量，F为外部载荷向量. 整体刚度矩阵K可由单元刚度矩阵装配得到, 表示为

(9)

其中Ωd为设计域Ω的离散域. 单元刚度矩阵为

(10)

式中的下标i1,i2表示影响该单元Ωe的控制点索引,λ,μ为Lamé常数, 与材料属性相关, 计算公式为

E为材料弹性模量,ν为材料Poisson比.

2.2 离散多孔结构特征参数分布

本文采用B样条函数建立多孔单元特征参数分布, 在二维设计域内任意一点的多孔单元特征参数值可由下式计算:

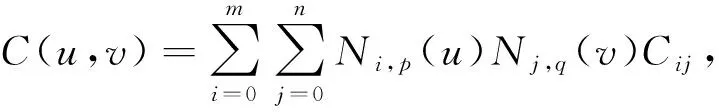
(11)

其中Cij表示控制点处的多孔单元特征参数变量. 为简化计算过程, 本文以单元内恒定的特征参数进行结构分析. 以等几何单元中心点的特征参数值作为该单元的特征参数值, 表示为

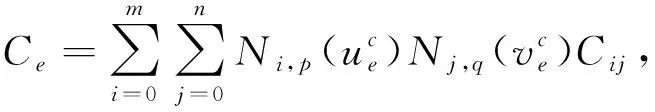
(12)

(13)

基于B样条的多孔单元特征参数分布是光滑连续分布函数, 这种表示方法相当于对特征参数分布施加了光滑效果, 可有效避免在有限元分析中以单元进行拓扑优化出现的棋盘格或孤岛现象, 这是基于B样条参数化设计的一个显著优势.

3 多孔结构的拓扑优化

3.1 最小柔度优化理论

结构拓扑优化最早是设计轻量化结构[39], 其中固体各向同性材料惩罚模型(solid isotropic material with penalization, SIMP)[40]应用最广泛, 其通过在每个材料单元引入相对密度, 再优化材料密度的分布, 所以也称为变密度法. 这种优化算法对目前多孔结构的优化非常有用, 通过建立多孔单元特征参数分布与材料相对密度间的映射关系, 然后在变密度法框架下基于等几何分析求解优化问题, 实现最佳性能的多孔单元特征参数分布, 提高多孔结构的性能.

3.2 优化函数

下面介绍多孔结构优化设计中的拓扑优化算法, 结构的总势能[39]表示为

(14)

本文基于最小柔顺度优化问题, 确定多孔单元特征参数在设计结构中的分布, 使得柔顺度最小化, 即最小化总势能, 以使柔顺度达到最小. 优化问题的数学表达式为

(15)

其中:k1,k2为多孔单元特征参数与材料相对密度函数系数(见表2);Cij为多孔单元特征参数分布控制点, 即函数优化变量；Ce为等几何单元中心特征参数(式(12))；t为密度惩罚因子, 本文取值为3； 第一个约束条件KU=F为弹性平衡方程, 表示位移向量U在外部载荷向量F下满足平衡方程条件； 第二个约束条件为材料体积约束,V(·)表示多孔结构相对体积函数,Ve表示等几何单元体积,V0表示设计域总体积,τ为给定体积分数, 表示优化后的多孔结构材料体积必须满足给定材料体积量； 第三个约束条件为特征参数的约束, 表示特征参数约束在有效范围内, 确保可构建完整的多孔单元.

3.3 灵敏度分析

下面推导在变密度框架下等几何拓扑优化的灵敏度计算公式, 优化变量为样条控制点处对应的多孔单元特征参数变量. 首先, 柔顺度关于优化变量的偏导数计算公式为

(16)

结合式(13)可得

(17)

其次, 材料体积关于优化变量的偏导数计算公式为

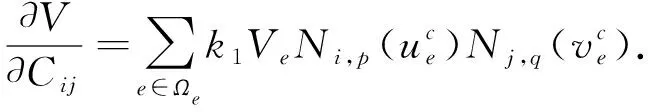
(18)

本文采用优化准则法求解优化问题(15), 参考文献[39], 利用启发式迭代更新优化变量:

(19)

其中:m是移动步长, 本文取值0.2;η(0<η<1)是阻尼系数, 本文取值0.5;Bij表达式为

式中γ是Lagrange乘子, 可利用二分法求解.

3.4 多孔结构生成

通过上述结构优化后, 实现了在设计域中的最佳多孔单元特征参数分布, 该多孔单元特征参数分布同样可定义在参数域中. 由于本文研究平面应力问题, 因此在求解结构优化时设计域及其对应的参数域均为二维, 而实际薄板及多孔结构均为三维. 由于平面应力分析不受第三个维度的影响, 因此可直接将多孔单元特征参数分布和几何模型控制点映射到第三个维度上, 采用三变量B样条函数进行表示：

(20)

此时多孔单元特征参数分布映射三元函数C(u,v,w)定义在几何体参数域内, 则隐式曲面的函数表达式修改为

ψ(u,v,w;αu,αv,αw)=C(u,v,w),

(21)

其中(αu,αv,αw)表示周期参数, 即多孔单元在对应方向的个数. 本文固定αw=1, 使得薄板厚度对应一个多孔单元; 再利用移动四面体方法提取等值面, 构建参数域多孔结构; 最后利用薄板B样条体函数(式(4))将参数域空间中的多孔结构映射到物理域中, 即得到经过等几何拓扑优化后的薄板多孔结构. 特别地, 在参数域中生成多孔结构再投影回物理空间中, 可保证所有的多孔单元都是完整的, 这是由于参数域是规则的, 而实际几何模型并非规则模型.

在悬臂梁多孔结构的拓扑优化设计中, 多孔单元为G型单元. 首先设计优化问题, 并通过拓扑结构优化求解获得最佳多孔单元特征参数分布, 再将该多孔单元特征参数分布投影回二维参数域中; 然后将特征参数分布拓展至三维获得三维的多孔单元特征参数分布, 再基于式(21)利用移动四面体方法提取等值面, 构建参数域多孔结构； 最后经过三元B样条函数的映射将参数域多孔结构映射到物理域中, 实现一定体积分数下最佳性能薄板多孔结构的构建. 多孔结构优化设计算法流程如图5所示.

图5 多孔结构优化设计算法流程Fig.5 Workflow of porous structure optimization design algorithm

4 实验结果与分析

下面给出一些实验案例, 并进行分析. 为简化计算过程, 实验部分数据均采用无量纲量, 包括单位集中载荷为1, 弹性模量E=1, Poisson比ν=0.3. 实验相关数据列于表3.

4.1 悬臂梁

图5已给出了基于悬臂梁优化算法的流程, 其中悬臂梁左侧固定, 在右下角施加单位集中载荷, 在体积分数为0.4的条件约束下, 基于G型多孔单元进行结构优化. 下面通过与传统有限元分析方法进行对比, 分析基于等几何分析进行多孔结构拓扑结构优化的优势. 特别地, 进行有限元分析的单元个数与等几何分析方法保持一致. 分别统计基于有限元方法和等几何方法求解拓扑优化问题的耗时, 结果表明, 利用等几何分析方法可有加速优化问题求解.

4.1.1 棋盘格现象

本文利用有限元方法对参数多孔结构进行拓扑优化, 其中每个分析单元对应一个特征参数变量, 作为优化变量进行拓扑优化, 最后得到一个在离散设计域的多孔单元特征参数分布, 如图6(A)所示. 对比如图6(B)所示的用等几何分析方法的悬臂梁多孔结构特征参数分布, 利用有限元分析方法进行参数多孔结构的拓扑优化会产生严重的棋盘现象, 而等几何分析方法可有效抑制发生棋盘现象.

图6 多孔单元特征参数分布对比Fig.6 Comparison of porous element characteristic parameter distribution

4.1.2 多孔单元个数

传统有限元分析利用离散网格近似几何模型, 对离散网格单独进行优化, 多孔单元个数需与分析单元个数保持一致, 如图7(A)所示. 而基于等几何分析方法, 通过对等几何单元对控制点进行优化, 最后得到以B样条函数表示的多孔单元特征参数分布, 在构建多孔结构时多孔单元个数无需与等几何单元个数保持一致, 可通过修改式(21)中周期参数αu,αv调控多孔单元个数. 图7(B)和图7(C)分别为基于等几何分析方法进行拓扑优化后构建的两种不同多孔单元个数的悬臂梁多孔结构.

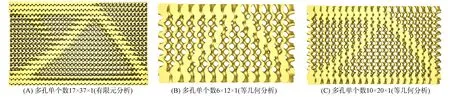
图7 多孔单元个数对比Fig.7 Comparison of number of porous elements

4.1.3 多孔单元连接

有限元方法以单元为分析目标, 在优化得到多孔单元特征参数分布后, 分别以分析单元的特征参数值构建多孔单元, 最后通过单元映射的方法将多孔单元映射到分析单元中生成多孔结构, 由于多孔单元特征参数分布存在严重的棋盘现象, 因此两两相邻多孔单元间无法保证光滑连续. 如图8(A)所示, 多孔结构中相邻的多孔单元间不能光滑连接, 通常需要对多孔结构进行光滑处理, 这会改变拓扑优化的结果.

而基于等几何分析的方法, 以多孔单元特征参数变量控制点为优化目标, 最终获得一个光滑分布函数, 再将该函数代入式(21), 可构建一个光滑连续的等值面, 基于该光滑连续等值面构建的多孔结构, 可保证多孔单元间光滑连续, 如图8(B)所示.

图8 多孔单元间连接性对比Fig.8 Comparison of connectivity between porous elements

4.2 MBB

图9为平面应力状态下MBB(miniature bending beam)的几何模型, 其中图9(A)的MBB左下角受滚动铰链约束, 右下角固定支撑, 梁上部中点处受单位集中载荷, 在体积分数为0.45的约束条件下, 基于P型多孔单元进行拓扑结构优化, 优化后多孔单元特征参数分布在设计域中, 如图9(B)所示, 最后生成的多孔结构如图9(C)所示.

图9 MBB多孔结构拓扑优化(P型多孔单元)Fig.9 Topology optimization for porous structure of MBB (P type porous element)

4.3 1/4圆环

图10为平面应力状态下1/4圆环结构的几何模型, 其中图10(A)的1/4圆环模型底边固定, 在左上角处受单位集中载荷, 在体积分数为0.45的约束条件下, 基于D型多孔单元进行拓扑结构优化, 优化后多孔单元特征参数分布在设计域中, 如图10(B)所示, 最后生成的多孔结构如图10(C)所示.

图10 1/4圆环多孔结构拓扑优化(D型多孔单元)Fig.10 Topology optimization for porous structure of quarter annulus (D type porous element)

4.4 多载荷悬臂梁

对多载荷的情形本文也进行了实验分析, 图11为多载荷下悬臂梁的几何模型, 其中图11(A)的悬臂梁左侧固定, 在右侧上下两端点处分别受反向的单位集中载荷, 在体积分数为0.4的约束条件下, 基于IWP型多孔单元进行拓扑结构优化, 优化后多孔单元特征参数分布在设计域中, 如图11(B)所示, 最后生成的多孔结构如图11(C)所示.

图11 多载荷悬臂梁多孔结构拓扑优化(IWP型多孔单元)Fig.11 Topology optimization for porous structure of cantilever beam under multiple loads (IWP type porous element)

综上所述, 本文提出了一种基于变密度框架下的参数多孔结构等几何拓扑优化方法. 首先, 基于TPMS设计多孔单元, 并分析多孔单元特征参数与材料相对密度分布间的关系; 其次, 考虑薄板多孔结构平面应力的静态平衡问题, 以多孔单元特征参数为优化对象, 利用变密度框架下的等几何分析方法在材料均匀分布的设计空间实现最佳的特征参数分布; 最后, 利用优化后的多孔单元特征参数分布构建多孔结构, 实现了同等材料体积下力学性能最佳的多孔结构设计. 由于等几何单元间具有高阶连续性, 因此保证了应力函数的连续性, 提高了计算精度与效率. 此外, 多孔单元特征参数分布用样条形式表示, 方便调控多孔结构中的多孔单元数, 且保证了多孔单元间的光滑连接.