基于可变遗忘因子的递推最小二乘法锁相环研究
2021-01-15辛瑞芝卢佳南曹文华刘鼎立刘树通
辛瑞芝,戴 宁,卢佳南,曹文华,刘鼎立,刘树通
(山东电工电气集团新能科技有限公司,济南 250101)
0 引 言
在可再生能源并网逆变器、脉冲宽度调制(PWM)整流器和有源电力滤波器等并网系统中,能否得到准确的电角度是整个系统稳定运行的关键。在理想情况下,ABC三相电压幅值相等,且每相相位相差120°。然而在实际工况下,由于存在三相电压不平衡、谐波干扰等问题会导致出现相位偏移。因此,在实际工况下必须提高相角估计的快速性和鲁棒性,从而获得更加准确的角度[1]。
目前在电力系统中的相位同步技术使用最广泛的是锁相环。采用过零比较方式获取相位差的信号是传统的锁相环技术主要所采用的方法,电网电压的过零点的检测由硬件电路实现[2-3]。由于系统中存在电压畸变,导致电压信号零点和基波零点不一致的情况,甚至在基波零点附近可能会出现多个过零点信号[4-5],因此基波正序电压的过零点并不能被准确地确定,锁相的精度会受到较大的影响,而且传统锁相环技术还存在动态性能较差的缺陷[6]。
针对传统锁相环技术的不足,本文提出一种基于可变遗忘因子的递推最小二乘算法的锁相方法。该锁相方法在现有递推最小二乘法基础上引入了可变遗传因子,提高了系统的抗干扰能力,最终达到提高检测精度的目的。
1 基于同步旋转坐标系的锁相环原理
锁相环可以实现对交流信号的相位的跟踪和锁定,在逆变电源的启动瞬间即可对电网相位进行跟踪,以减少由电源切换原因对负载产生的突变电流[7]。给出传统锁相环的基本工作原理:当电网电压平衡时,电网电压中只包含正序电压分量,此时,给出在两相静止坐标系αβ和两相同步旋转坐标系dq中的实际电压矢量以及锁相环输出电压矢量位置,如图 1所示。当电网电压的幅值即合成矢量e的大小不变时,e的q轴分量eq可以反映出d轴和电网电网e的相位关系[8]。当eq>0时,电网电压e超前d轴,此时增大同步信号的频率;当eq<0时,电网电网e滞后d轴,此时减小同步信号的频率;当eq=0时,电网电压e和d轴同向。通过分析可知,通过控制eq=0实现两者同相位。
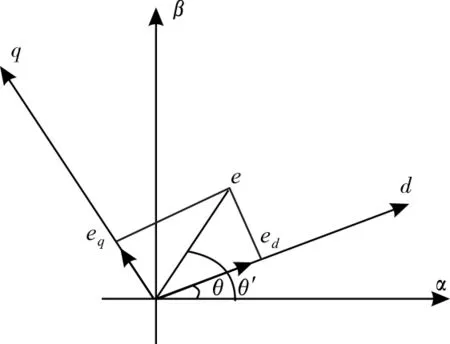
图1 设计方案电路原理图
2 基于可变遗忘因子的递推最小二乘法锁相环
在理想电网条件下,三相电压为
(1)
通过Clark变换,将三相静止abc坐标系下的三相对称电压ua、ub、uc转化成两相静止αβ坐标系下的两相正交电压uα、uβ,给出转换为
(2)
在实际工况下,由于三相电压不平衡,导致谐波、相位偏移、频率突变等现象经常出现,这些现象会对锁相的精确度产生影响。
根据Heydermann教授的方法,理想和实际情况下的电压输出量可以表示为
(3)
根据式(3),补偿电压uα1和uβ1可以表示为
(4)
根据uα2和uβ2满足平方和为1的关系,可得:
(5)
式(5)可改写成式(6):
(6)
其中,ki,i=1,2,…,5可以采用遗传因子的递推最小二乘算法进行估算。
α,G,fa,fb,Aa可以采用ki进行表示:
(7)
根据递推最小二乘法,式(6)可以表示为
y(n)=k(n)x(n)
(8)
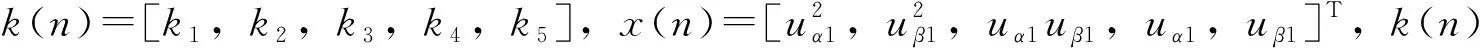
(9)
(10)
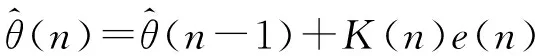
(11)
(12)
在经典带遗忘因子递推最小二乘法算法中,λ被设定为一个固定值,也就是按固定速率削弱过去观测数据的作用。当λ接近1时,该算法精度提高但对参数的跟踪能力降低[9]。降低λ的值可以提高对参数的跟踪能力,但同时也会降低算法的稳态精度。
为了满足算法的精度和对参数跟踪能力这两种矛盾的需求,本文提出如图2所示的基于可变遗忘因子的递推最小二乘法锁相环算法。
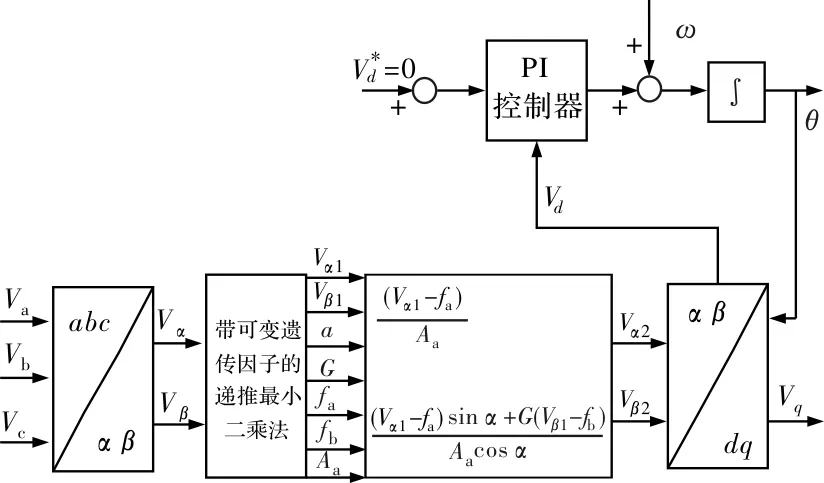
图2 基于可变遗忘因子的
递推最小二乘法锁相环算法图
式(9)中的e(n)根据第n-1周期的参数估计值计算得到,是先验误差[10]。后验误差可以定义为
(13)
从式(9)、式(11)和式(13)得:
ε(n)=e(n)[1-φT(n)K(n)]
(14)
通过在误差信号中恢复系统噪声来设计遗忘因子的取值,即遗忘因子λ(n)可以根据式(14)进行调整:
E{ε2(n)}=E{v2(n)}
(15)
式中,E{ε2(n)}=σ2(n)为系统噪声功率。
将式(10)和式(14)代入式(15)得:
(16)

(17)
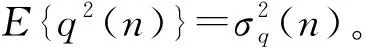
(18)
式中,α为加权因子。
考虑到λ的取值必须在[0,1]范围内,本文提出算法的遗忘因子可以按下式给出:
(19)
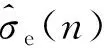
3 仿真结果
通过对基于可变遗忘因子的递推最小二乘法锁相环的工作原理和基本结构的分析,在Matlab中对其进行仿真,仿真结果如图3所示。从图中可以看出基于可变遗忘因子的递推最小二乘法锁相环可以正确锁相,验证了其功能的准确性。
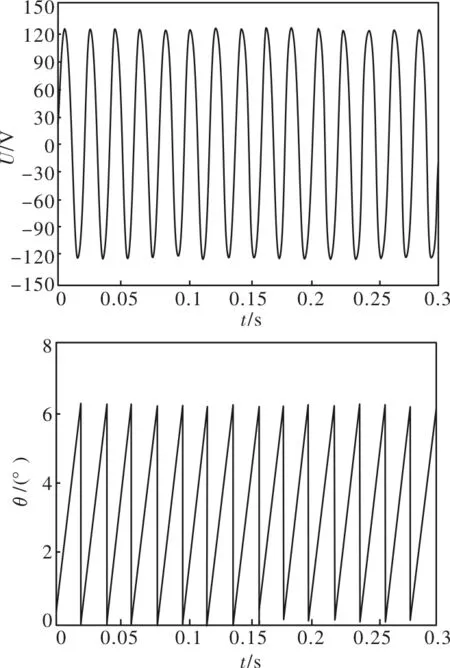
图3 本文算法仿真波形图
当系统A相电压发生突变时,例如在0.04秒时幅值增加一倍,给出A相电压突变的仿真波形图如图4所示。通过仿真图可以看出当系统电压发生波动时,基于可变遗忘因子的递推最小二乘法锁相环仍可以快速精确地锁住电压频率,且波动及误差较小。给出最小二乘法锁相环在系统电压波动时的仿真图如图5所示,当电压发生波动时,锁相环也会发生变化,不能准确地锁住电压相位。
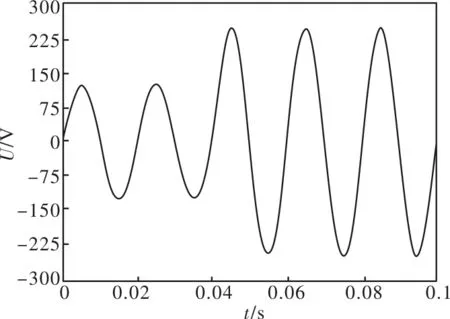
图4 A相电压突变时本文算法仿真图
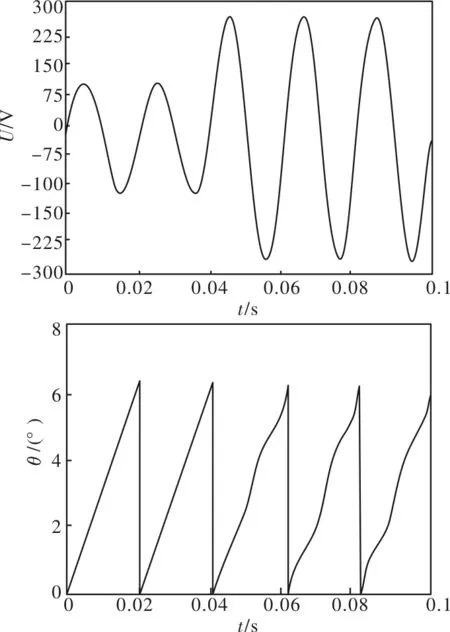
图5 A相电压突变时最小二乘法锁相环仿真图
当系统频率发生突变时,即在0.1 s之后频率突增至100 Hz,在0.2 s之后频率又恢复原频率50 Hz,给出频率发生突变时的仿真波形如图6所示,突变时的局部放大图如图7(a)和图7(b)所示。
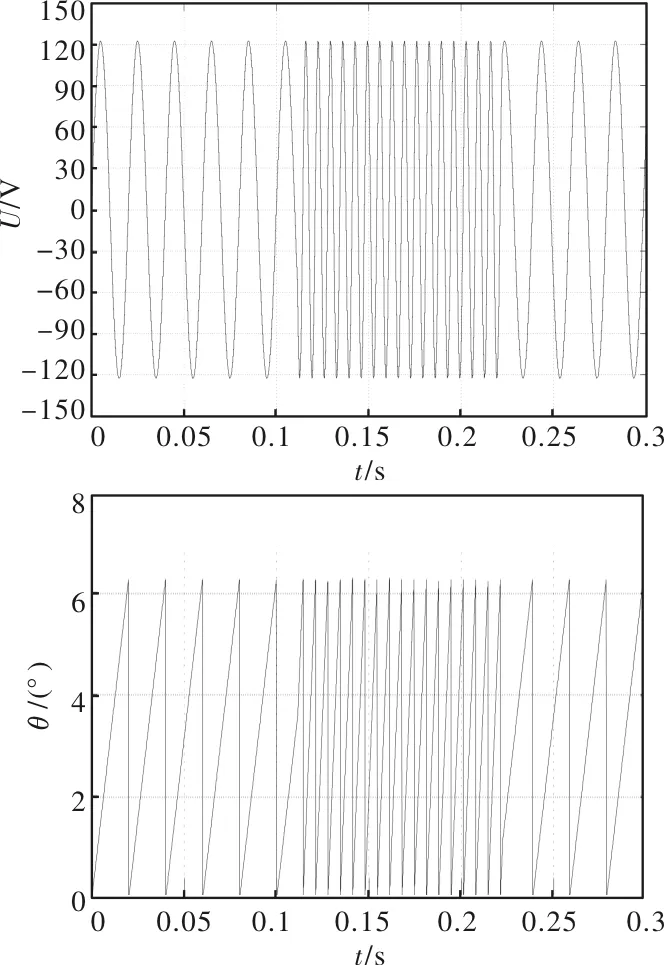
图6 频率突变时本文算法仿真图

图7 频率突变情况下局部放大图
从图中可以看出当频率发生突变时,带有变遗传因子的最小二乘法锁相环可以快速反应,在频率突变后的第一个周期内即可稳定锁住电网频率,完成对频率的重新锁相且锁相准确。
4 实验结果
将本文锁相环算法应用于试验样机中 ,所得到的波形如下所示。图8给出当电压发生突变时试验波形。可以看出,当电压发生突变时,本文锁相环算法可以稳定锁住电压频率,准确地实现锁相。图9给出当电压频率改变的试验波形,可以看出当频率变化时,本文锁相环算法也可以实现稳定锁相。

图8 电压突变时试验波形

图9 频率改变的试验波形
5 结 语
通过Matlab仿真及样机试验可以得出,当系统出现相电压突变时,基于可变遗忘因子的递推最小二乘法锁相环可以快速准确地锁住电压,完成锁相。结果表明该算法可以有效提高锁相环的精度和可靠性,提高系统的抗干扰能力。
