一种在铣削实时仿真中基于二叉树网格划分方法
2021-01-15成建群
成 建 群
(苏州健雄职业技术学院中德工程学院 江苏 太仓 215411)
0 引 言
铣削仿真就是利用计算机模拟铣刀沿着铣削轨迹与被加工工件(毛坯)之间的相对运动,实现对加工中铣刀移动、铣削等过程的监控和验证[1]。当前铣削仿真中几何模型主要有线框模型、图像空间模型、实体模型和离散矢量模型[2]。实体模型方法用数学模型描述几何体,保留了全部的数据,计算结果精确可控,可以进行旋转、缩放等几何变换和数据分析测量。但是实体模型在铣削仿真中求交计算量大,仿真速度慢。留量几何模型基于实体模型方法,以网格来模拟工件表面,通过网格Z方向(或矢量方向)的值来表示工件上留存的材料。仿真时,通过修改网格节点的Z值来模拟工件表面的变化,简称为Z-Map方法。该方法在车削[3]、磨削[4]和铣削[5-6]等仿真中得到了广泛的应用。
在留量几何模型中网络数量的多少直接关系到计算量的大小,占用内存的多少,响应速度的快慢。而实时仿真要求计算速度快、响应及时,同时占有内存空间小。在铣削仿真时,传统研究中绝大多数首先对工件整体进行网格划分,然后进行仿真计算。本文提出一种二叉树的网格表示方法,仅仅对需要铣削仿真的区域进行网格细分,快速响应仿真过程。
1 二叉树网格表示方法
三角形网格具有模型简单、仿真精度可控、实时性好、视角连续可变等优点,在加工仿真、虚拟加工领域应用广泛[7-9]。这里讨论的网格均是三角形网格。为了节省内存空间,3D模型用顶点和三角形表示(n个顶点,m个三角形),即:
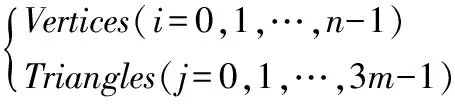
(1)
三角形的顶点顺序表示三角面的朝外法向。三角形中仅保存顶点的序号,第k+1个三角形顶点为Triangles[3k]、Triangles[3k+1]、Triangles[3k+2]。三角形的边按顶点顺序分别标记为0、1、2。同时边分为父边(P)、左边(L)、右边(R),与顶点顺序一致,如图1所示。每一个三角形有且仅有一个父边、左边、右边。
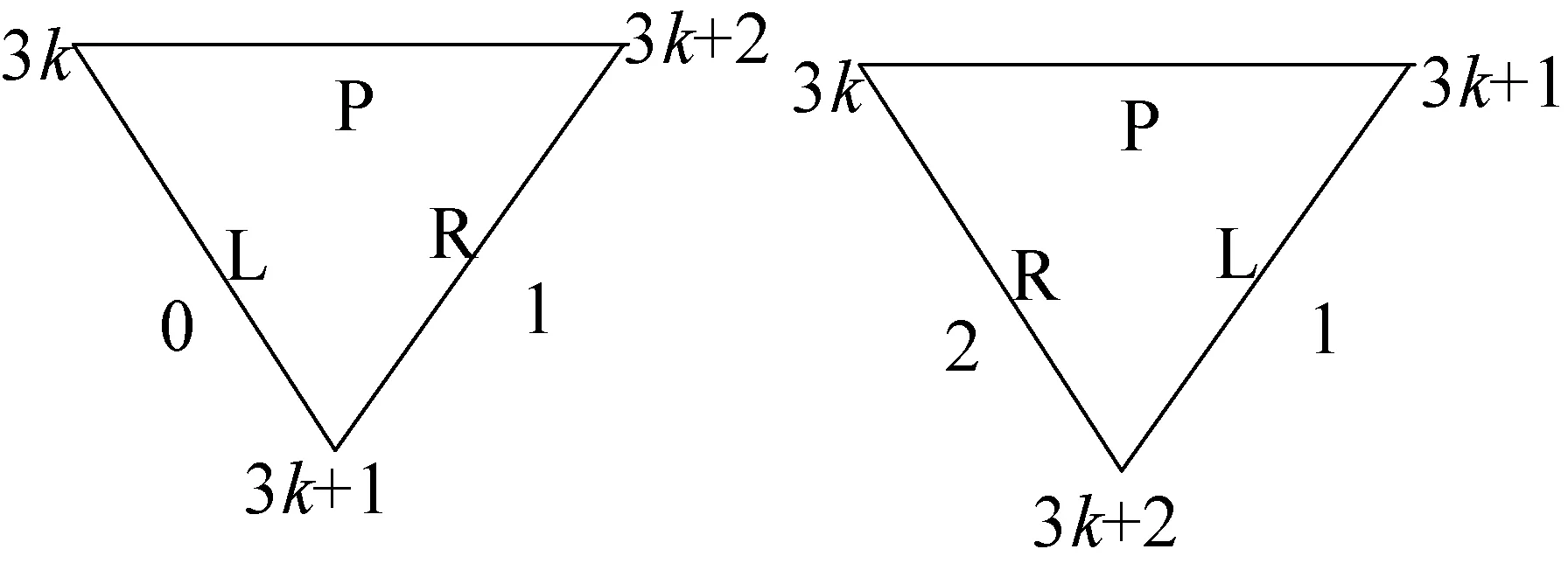
图1 顶点与边关系
三角形作为二叉树的节点,左边与二叉树左节点的父边共边,右边与二叉树右节点的父边共边。如图2所示,三角形1左节点为三角形2,右节点为三角形3。进一步可以看出,三角形1的顶点序号为Triangles[0]、Triangles[1]、Triangles[2],三角形2的顶点序号为Triangles[3]、Triangles[4]、Triangles[5],三角形3的顶点序号为Triangles[6]、Triangles[7]、Triangles[8]。
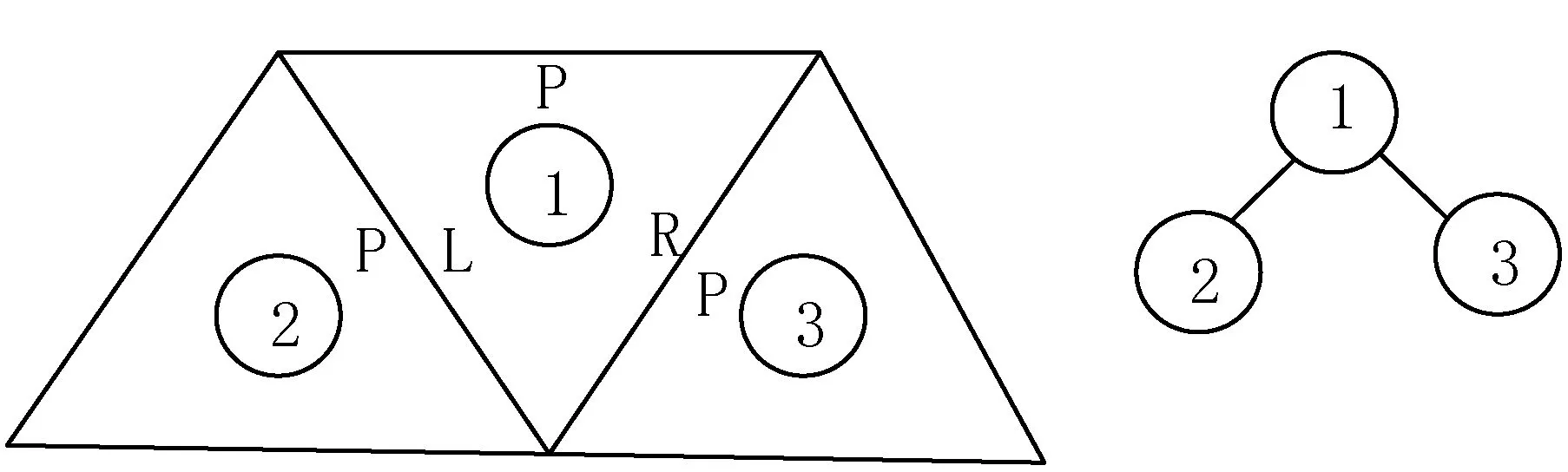
图2 二叉树构成
经以上分析,m个三角形构成的3D模型可以表示为一个由m个节点构成的二叉树,每个节点代表一个三角形,二叉树的节点关系表示了三角形的共边关系,即:
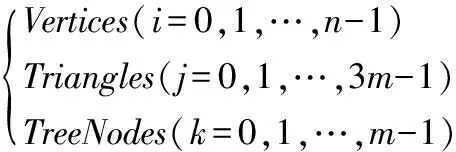
(2)
2 二叉树网格的创建
创建二叉树网格时,原来所有的三角形构成了一个三角形库(Triangles)。在三角形库中任选择一个三角形作为起始三角形,以该三角形任一条边为父边,并确定左边和右边,得到树节点库(TreeNodes)的第一个树节点。寻找与左边、右边共边的另外三角形,该共边为父边。再从以此为父边的新三角形继续遍历查找,直到所有的三角形均查找完成,最终可得到完整的树节点库,即完成二叉树网格的创建。处理流程如图3所示。立方体三角形网格按流程图可以得到如图4所示结果,左侧为立方体的网格及三角形标识,右侧为该立方体网格的二叉树。

图3 二叉树创建流程
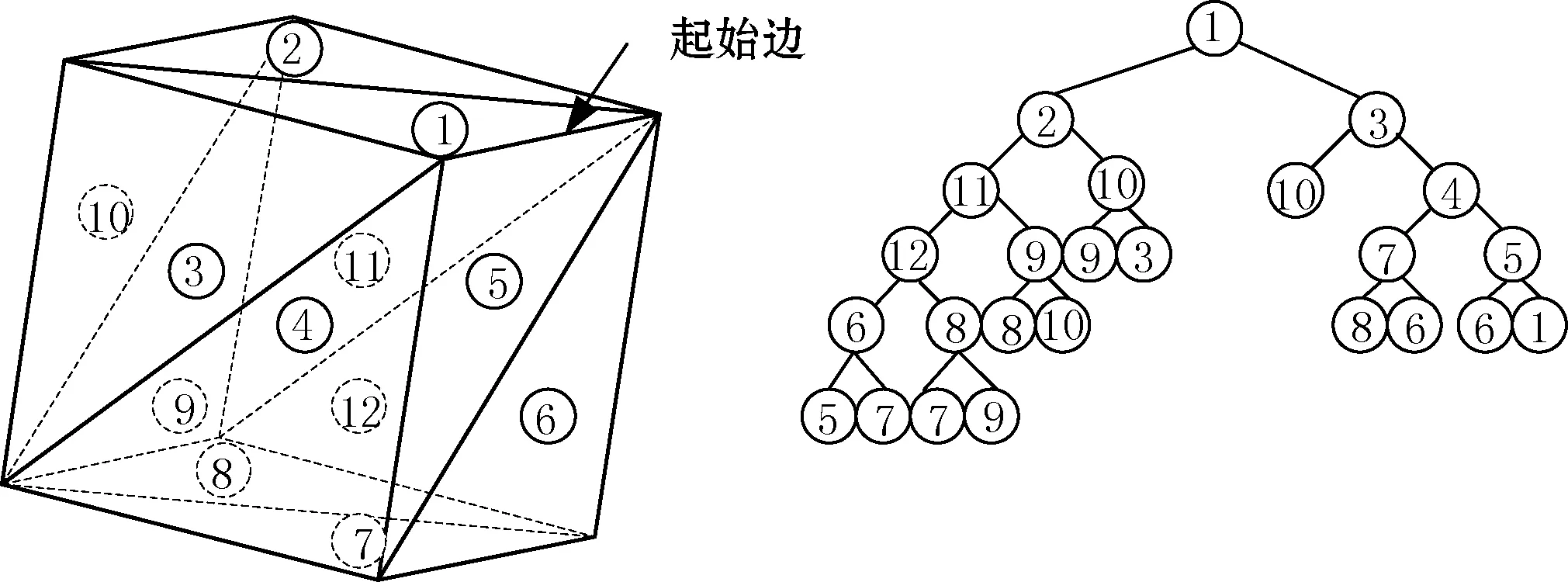
图4 立方体网格的二叉树
3 二叉树网格的划分
3.1 共边两网格单元的划分
在铣削仿真中网格随铣削区域进行细分,首先就是要对网格单元划分。相邻的网格单元划分,取公共边中点,原来的两个三角形划分为四个三角形,产生一个新的顶点。在网格二叉树中,相邻网格有两种关系:父子共边网格和无父子共边网格。
(1) 父子共边网格。如图4所示,网格三角形1和2相邻,用虚线划分,生成网格三角形1、2、3、4。网格三角形1的左边或右边与网格三角形2的父边一致。因共边的端点次序可能不一致,构成四种情况。可以依照图5中结构关系,修改网格二叉树数据。处理流程如图6所示。
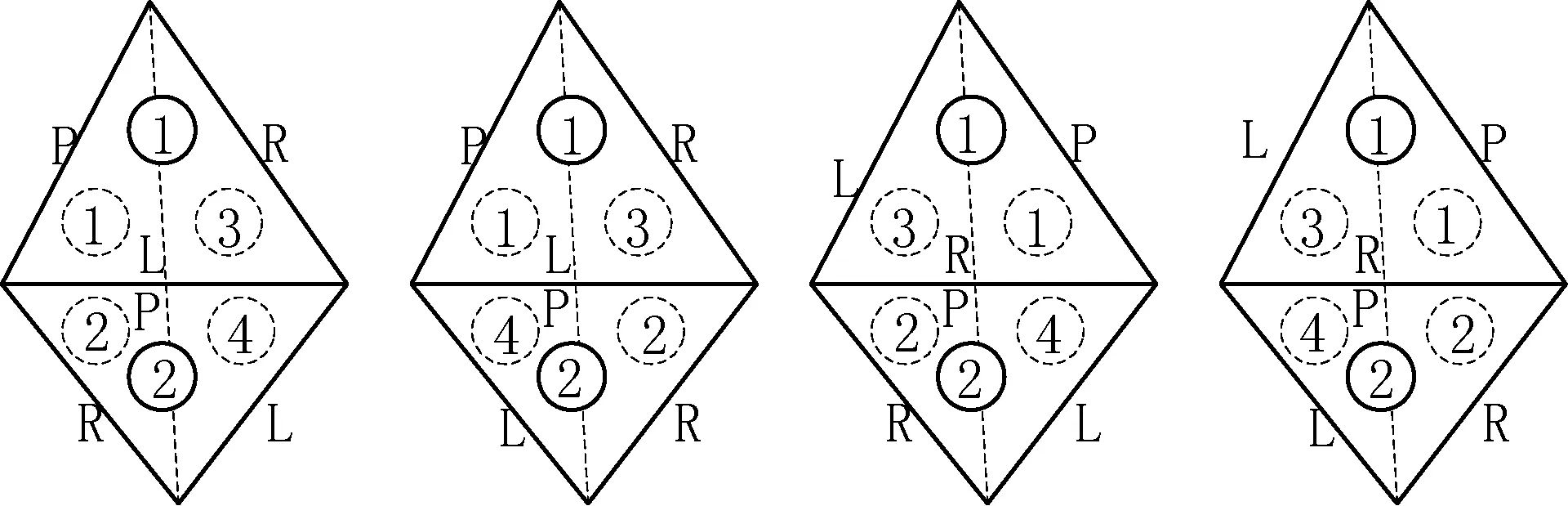
图5 父子共边网格划分
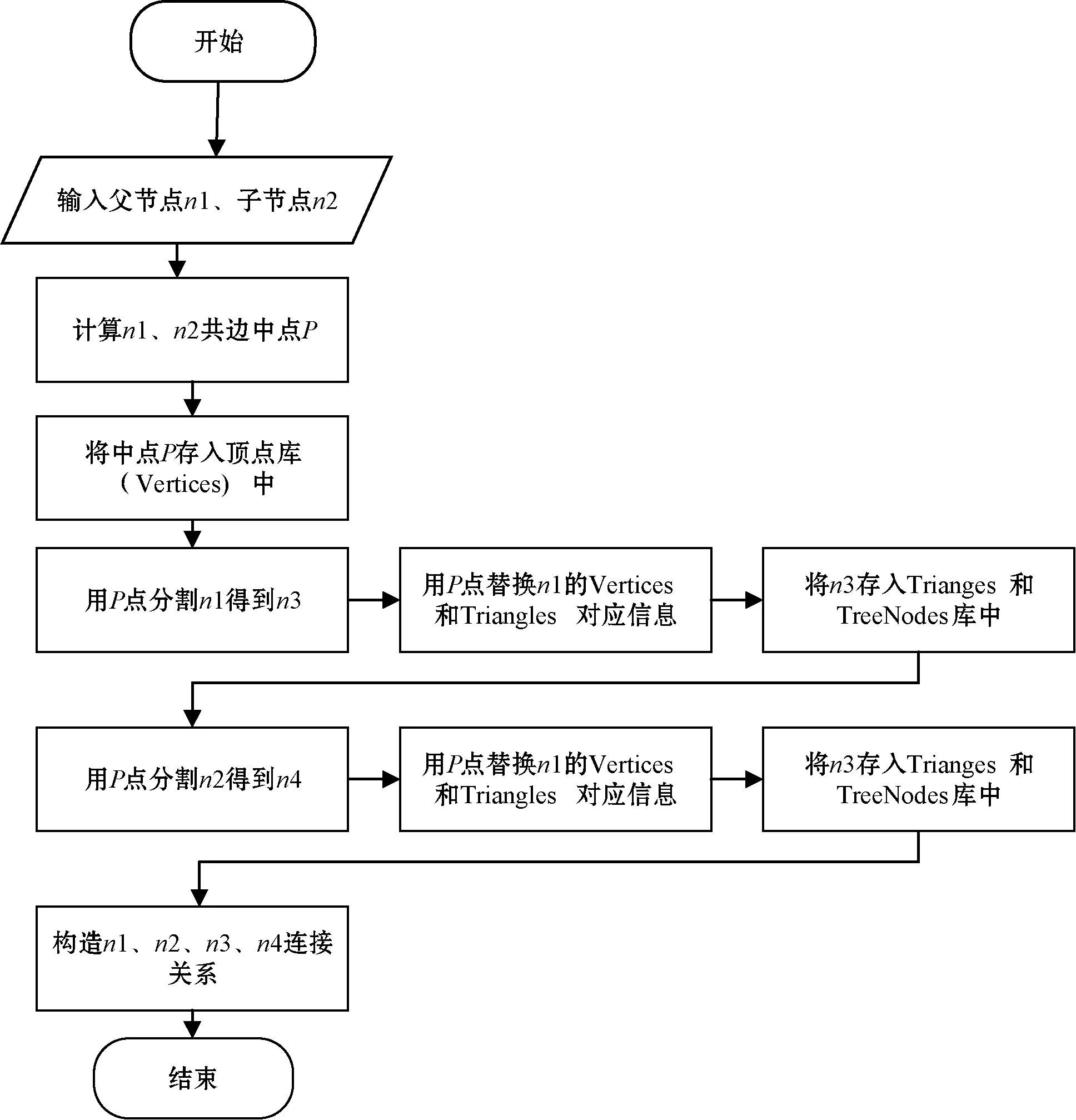
图6 父子共边网格处理流程
(2) 无父子共边网格。无父子共边网格处理流程与父子共边网格处理流程一致,但无父子关系共边的三角形因两个三角形共左边与共右边、顶点次序相同与相反共有八种情况(如图7所示)。划分网格后,三角形划分后的二叉树的结构仅仅与公共边为左边还是右边有关,不妨称为左连接、右连接。三角形1划分后变为1、3,三角形2划分后变为2、4,并且1、3为父子关系,2、4为父子关系,可以得到如表1所示的关系。
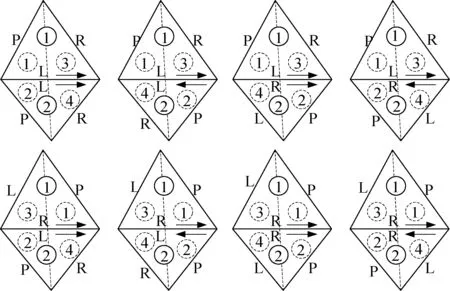
图7 无父子共边网格划分
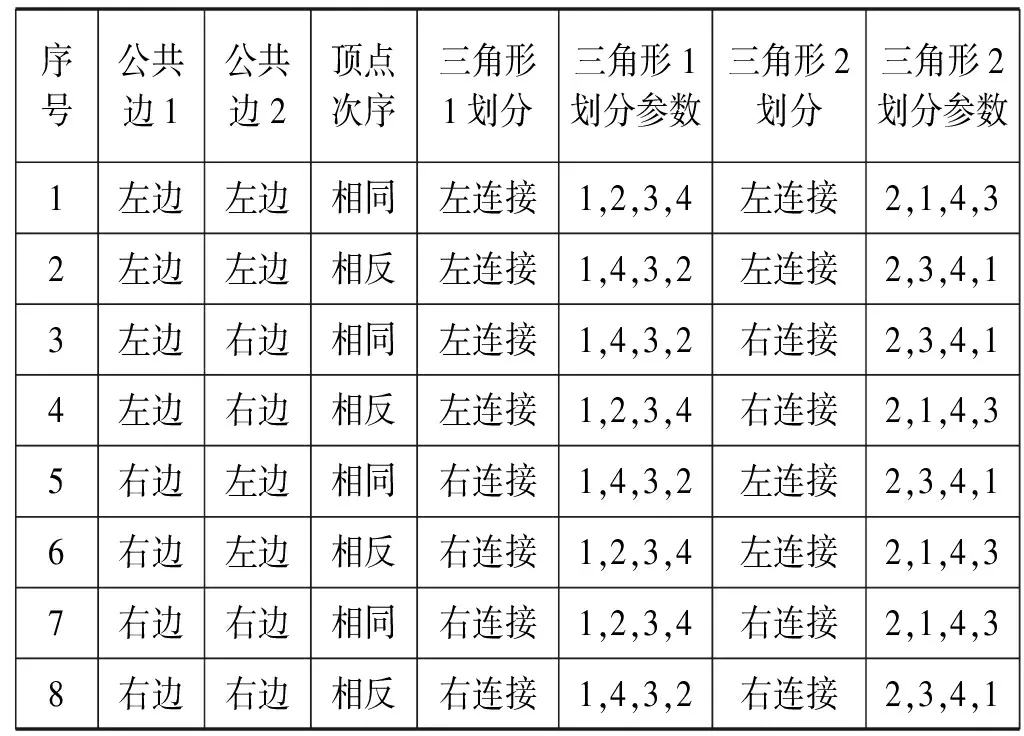
表1 无父子共边网格划分
3.2 左右连接关系分析
如图8所示,网格中n1、n2的公共边划分后产生n1、n2、n3、n4,为了表述方便,不妨记原n1为N1。二叉树节点N1进行划分生成n3,n1与n2共边,n3与n4共边,从图8不难看出对于左连接(仅仅需要考虑n1、n3的关系),左边为公共边,n3的父节点为n1,n3的左节点为n4,n3的右节点为原n1的右节点。即得到以下关系:

(3)
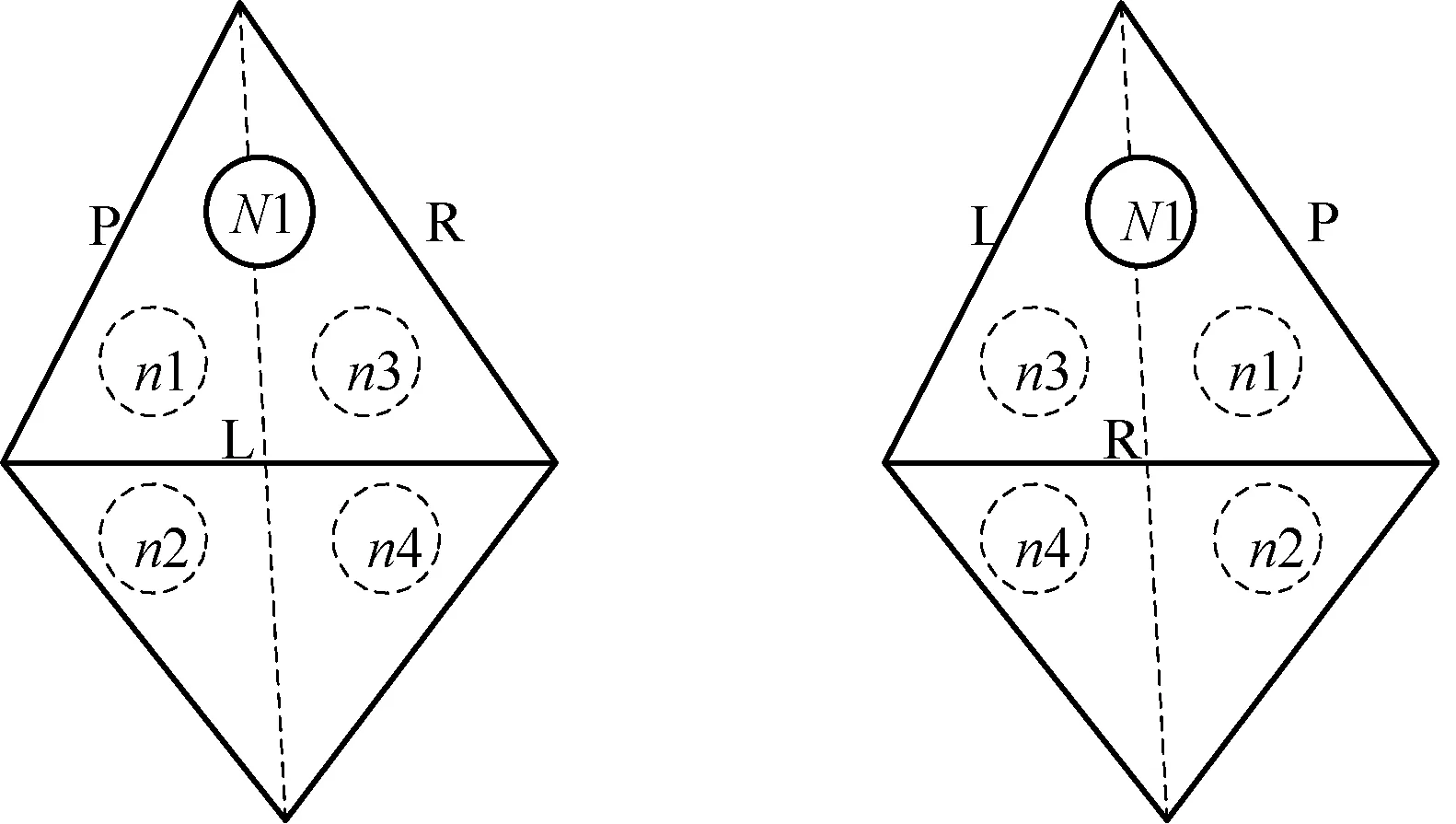
(a) 左连接 (b) 右连接图8 左右连接关系
原n1(N1)的右节点与N1的关系需要修改为与n3的关系。若原n1的右节点的父节点为原n1,则原n1的右节点的父节点为n3。否则,若原n1的右节点的左节点为原n1,则原n1的右节点的左节点为n3。否则,若原n1的右节点的右节点为原n1,则原n1的右节点的右节点为n3。即得到以下关系:
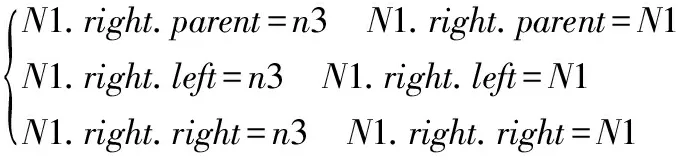
(4)
另外,n1的父节点保持不变,n1的右节点为n3,n1的左节点为n2。即得到以下关系:
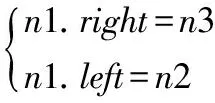
(5)
从图8不难看出,对于右连接(仅仅需要考虑n1、n3的关系),右边为公共边,n3的父节点为n1,n1右节点为n4,n3的左节点为原n1的左节点。即得到以下关系:
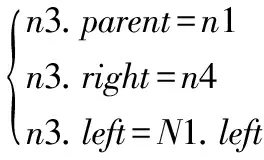
(6)
原n1(N1)的左节点与N1的关系需要修改为与n3的关系。若原n1(N1)的左节点的父节点为n1,则原n1的左节点的父节点为n3。否则,若原n1的左节点的左节点为原n1,则原n1的左节点的左节点为n3。否则,若原n1的左节点的右节点为原n1,则原n1的左节点的右节点为n3。即得到以下关系:
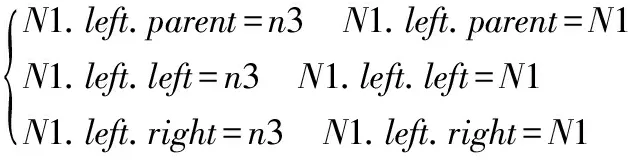
(7)
另外,n1的父节点保持不变,n1的左节点为n3,n1的右节点为n2。即得到以下关系:
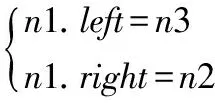
(8)
根据以上分析,可以完成左右连接的处理函数,分别记为:

左右连接形式参数序列均为n1、n2、n3、n4,表示两个相邻节点划分后产生四个节点,并且节点n1划分后产生n3,且n1与n2相邻,n3与n4相邻。
在应用表1关系时,以表1序号3为例,节点n1、n2进行划分产生n3、n4,n1的左边与n2的右边共边,顶点次序相同。构造二叉树关系时,n1、n3关系为左连接,参数为n1、n4、n3、n2,即相当于n1划分后产生n3,且n1与n4相邻,n3与n2相邻。调用过程如下:
LeftLink(n1,n4,n3,n2)
n2、n4关系为右连接,参数为n2、n3、n4、n1,即相当于n2划分后产生n4,且n2与n3相邻,n4与n1相邻。调用过程如下:
RightLink(n2,n3,n4,n1)
这样处理大大简化了程序判断,提高了处理效率,节省了响应时间。
3.3 铣削区域网格的划分
在铣削仿真时,工件表面需要变化的网格区域是刀具运动在网格表面的投影区域。为了分析方便,不妨设投影区域为二维点t1、t2围成的矩形区域。当网格与本区域相交或在本区域内就需要进行细分,直到满足细分最大面积的要求。
因切削区域是在工件表面的投影是连续的,所以从一个与切削区域相交或在切削区域内的三角形出发,通过事先构造的二叉树,就可以找到所有的相关三角形,并进行细分。为了不使细长三角形影响仿真效果,在切削区域内划分的两个三角形的共边必须为三角形的最长边。在切削区域边界处,若三角形在切削区域外或者三角形在切削区域上的投影面积为0,则该三角形的划分情况不影响切削仿真,没有细长三角形的要求,可以在非最长边上进行划分。区域网格划分流程如图9所示。
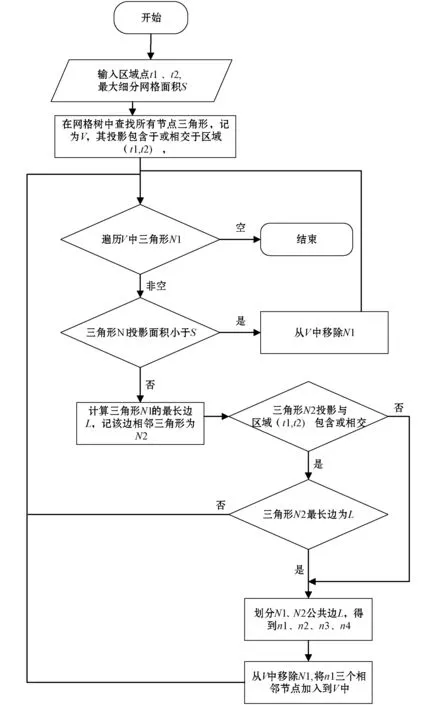
图9 区域网格划分流程
设铣削刀具半径为r,刀具中心由p1沿X轴或Y轴移动到p2(与Z轴运动无关),则铣削细分网格区域t1、t2满足以下关系:
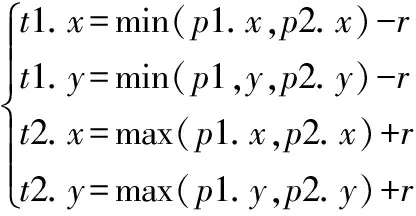
(9)
但是,考虑到切削区域边缘网格精度必须要将细分网格区域扩展一个细分网格单元。一般情况下,细分网格单元边长l与最大细分网格最大面积S满足式(10)。l过大造成细分网格浪费,过小会导致切削区域边缘网格拉扯明显,仿真效果差。
(10)
铣削细分网格区域顶点t1、t2修正如下:
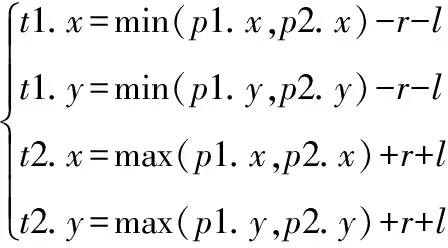
(11)
本文在Windows 10环境下,利用Unity3D实现了3D模型基于二叉树的网格表示方法。图10是对单位正方体上t1(0,0)、t2(0.2,0.5)矩形区域内网格进行划分的效果。可以看出,矩形区域内网格划分均匀,区域外网格数量少,达到了预期的效果。
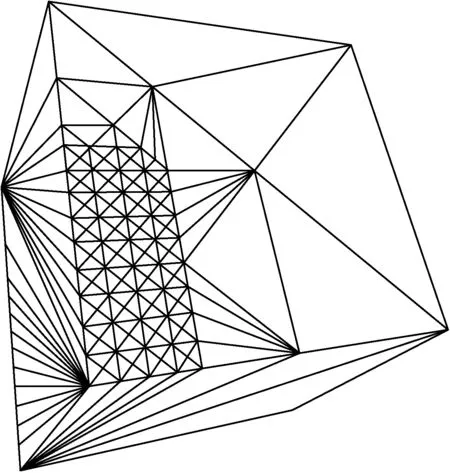
图10 区域网格的划分
4 仿真算例
进一步,基于Z-Map方法仿真和本文的网格表示方法可以仿真球头刀切削立方体毛坯,验证本文方法的性能。不妨假设工件为边长100的立方体,顶点坐标为(0,0,0)、(0,100,0)、(100,0,0)、(100,100,0)、(0,0,100)、(0,100,100)、(100,0,100)、(100,100,100),刀具垂直于工件表面(xoy平面)铣削工件,刀具球头半径为2,刀具球心由点(10,3,95)切削到点(10,40,90)。利用本文方法进行区域网格划分和全域网格划分,测试数据如表2所示。图11是单元网格最大面积是1时的区域网格与全部网格的仿真对比图。
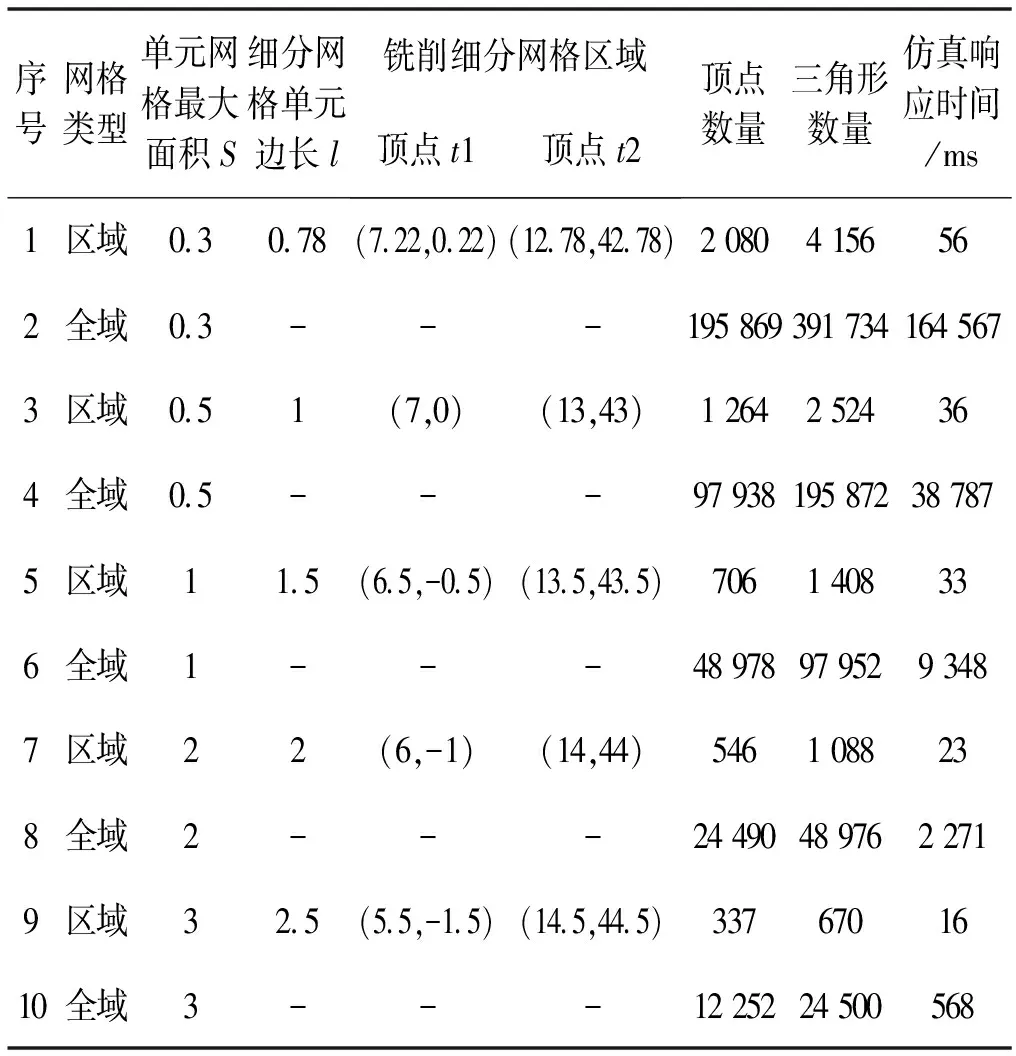
表2 区域网格仿真性能比较数据

(a) (b)图11 区域网格与全域网格仿真
顶点数量和三角形数量直接与占用内存成正比,顶点数量和三角形数量越大占用内存越多。用Z-Map方法铣削仿真时,模型上每一个顶点均需要进行判断或调整Z值,所以顶点数量直接关系到系统响应时间。单元网格最大面积越小,仿真精度越高,显示越精细。从表2的数据可以看出,全域网格仿真响应时间对单元网格面积大小非常敏感,采用区域网格仿真有明显优势。图12-图14为模具仿真加工实例。

图14 圆底槽仿真加工
5 结 语
本文提出一种3D模型的网格表示方法,用二叉树结构表示三角形网格边的组成关系,快速实现铣削区域网格划分,并基于Unity3D平台实现了Z-Map方法铣削仿真。结果表明,用二叉树结构表示区域网格划分相较于全域网格能够节省内存资源,加快仿真响应,提高仿真精度,能够应用于铣削加工仿真过程,满足实时性要求,有较高的应用价值。
