铁基超导体的输运性质*

李妙聪 陶前 许祝安2)†

1) (浙江大学物理学系,浙江省量子技术与器件重点实验室,杭州 310027)

2) (浙江大学,硅材料国家重点实验室,杭州 310027)

在铁基超导体中存在着多种有序态,例如电子向列相和自旋密度波等,从而呈现出丰富的物理现象.输运性质的测量能为认识铁基超导体的低能激发提供极为有用的信息.铁砷超导体由于其电子结构的多能带特性,其电阻率和霍尔系数与温度的关系出现多样性的变化,但在正常态并没有看到有类似铜氧化物超导体的赝能隙打开等奇异行为.在空穴型掺杂的铁基超导体中观测到霍尔系数在低温下变号,对应温区的电阻率上出现一个很宽的鼓包等,可能是从非相干到相干态的转变.热电势行为也表现出与铜氧化物超导体的明显差异,比如铁基超导体的正常态热电势的绝对值反而在最佳掺杂区是最大的,这也许跟强的带间散射有关.能斯特效应表明铁基超导体在 Tc 以上的超导位相涨落并不明显,与铜氧化物超导体存在明显差别.在铁基超导体上所显示出来的这些反常热电性质,并没有在类似结构的镍基超导体(如LaNiAsO)上观测到,镍基超导体表现得更像一个通常的金属.这些均说明铁基超导体的奇异输运性质与其高温超导电性存在内在的关联,这些因素是建立其超导机理时需要考虑进去的.

1 引 言

自2008年在电子型掺杂的LaFeAsO体系中发现超导临界温度高达26 K的超导电性以来[1],铁基超导体成为除铜氧化物高温超导体之外另一个新型高温超导材料家族,吸引了大量的研究.随后众多不同结构类型的铁基超导体相继被发现,按照其晶体结构划分,主要有四种类型,分别为“1111”型、“122”型、“111”型、“11”型.其中“11”型的FeSe 超导体,不仅结构简单,并且其电子结构中没有空穴型费米面,打破了原先对FeAs基超导体电子结构的认识[2,3].以FeSe作为基元,还衍生出一系列特殊的多层结构,例如在FeSe层间插入碱金属得到的 A Fe2-δSe2超导体（A代表碱金属元素）,或插入含氢氧根基团得到的“11111”型超导体(Li,Fe)(OH)FeSe[4,5]以及插入有机分子得到的超导体(CTA)xFeSe[6]和 (TBA)xFeSe[7].另外,还有近期发现的“1144”型[8]以及两个“122”型和一个“1111”型组合得到的“12442”型等超导体[9].这些铁基超导材料在结构上的共同点在于都存在FeAs(Se)层.此外,类似于铜基超导体,在铁基超导体中大多存在反铁磁序等与超导共存的序参量,因此,铁基超导体的正常态性质同样非常丰富,存在着自旋密度波 (spin density wave,即 SDW),轨道序和向列相等有序态,以及量子临界行为等.各种反常金属行为在输运性质上常表现出一些特征,例如在从高温一直到很低温下的线性电阻率是铜氧化物作为关联电子体系的一个标志性特征.输运性质往往是认识非常规超导体反常的正常态性质以及这些现象与超导电性之间的关系的一个重要线索,同时可以帮助我们更好地理解超导机理.

本文简要综述了铁基超导体的输运性质和热电性质,包括电阻率、霍尔系数以及热电势和能斯特效应,试图揭示铁基超导存在的低能激发的信息,并与铜氧化物超导体进行对比,期望推动对铁基超导电性的进一步理解.

2 电阻率

2.1 不同体系中电阻率随着掺杂浓度的变化

大多数铁基超导体的母体都表现出具有反铁磁序的金属行为.通过空穴、电子、或者化学等价掺杂、施加高压等手段可以逐步压制母体的反铁磁序从而诱导出超导电性.但在不同的体系中,电阻率的变化与掺杂浓度之间的关系不尽相同,同时与掺杂的类型也存在着很大的关系,这与铜氧化物超导体有所不同.

“1111”型体系是最先发现的铁基超导体,也是目前为止发现的铁基超导中块体超导温度最高的铁基超导体系.以“1111”体系中的LaFeAsO为例,母体在TN～138 K 形成反铁磁序,Ts～156 K 处发生结构相变,这一结果也被穆斯保尔实验所证实[10].该结构相变和反铁磁有序,在电阻率与温度关系上可以清楚地看到对应变化.从“1111”体系母体的输运行为上可以看到,其金属性并不好,但区别于铜基超导体母体的绝缘体行为.而对其进行不同的掺杂,得到的电阻率行为不尽相同.在空穴型掺杂时,随着掺杂浓度的变化,电阻率上的异常逐渐被抑制,但仍会一直存在,甚至在最佳掺杂的相区也存在.继续增大掺杂浓度至超导电性消失时,电阻率在高温的异常鼓起仍然可以观测到[11][12].同时空穴型掺杂的浓度范围很小.总之,“1111”型体系中空穴型掺杂的情况仍有诸多不清楚的地方,存在着一些争议.在化学等价掺杂的体系中(例如P部分替代As),研究发现随着掺杂浓度的上升,正常态电阻率上的异常迅速被抑制[13].此外,研究还发现P掺杂的相图中存在两个超导区域[14],初始为反铁磁态,随着掺杂浓度上升,反铁磁被压制； 但随着进一步掺杂,在超导态消失后会出现另一个反铁磁态,而进一步的掺杂又会压制该反铁磁诱导出另一个新超导态.在上述两个不同区域的超导态中,可能存在不同的费米面结构.而在电子型掺杂的“1111”型体系中,随着掺杂浓度的上升,电阻率在高温的异常(对应反铁磁有序和结构相变)逐渐被压制直至消失,超导电性才会出现.在较高温度下,电子型掺杂体系的电阻率与温度之间的依赖关系几乎是线性的,而到了低温下则变成费米液体行为,似乎存在一个从非费米液体行为到费米液体行为的转变[15,16].有理论解释该转变为一种“非相干”到“相干”(incoherence-coherence)的转变,主要来源于洪德耦合定则的贡献[17].此外铁基超导体与铜基超导体相比的一个不同之处在于“1111”体系可通过对FeAs面中Fe位掺杂Co或Ni等原子引入电子而得到超导[18].而在铜基超导体中,一旦在CuO面内引入杂质就会破坏其超导电性.

在“122”型体系中,也存在类似的掺杂相图,但其电阻率的变化与“1111”不太相同.如图1(c)所示,在空穴型掺杂时,电阻率与温度之间的关系以及电阻率的量级随着掺杂浓度的改变基本保持不变[19,20],此外在较高温处均存在一个鼓包的行为,其代表了从“非相干”到“相干”电子的转变.而最近在过掺杂的 AFe2As2(A = K,Cs,Rb)的核磁共振(Nuclear Magnetic Resonance,即NMR) 实验则表明其为一种演生的近藤晶格(emergent Kondo lattice) 的行为[21].此外,有研究还发现电阻率在低温的行为发生了改变,并可对80 K以下的电阻率用公式ρ=ρ0+A×Tn(式中ρ和ρ0分别代表电阻率和剩余电阻率,A和n代表拟合参数)进行拟合更加清晰地看出： 在最佳掺杂浓度附近时,指数n趋向于1,电阻率与温度之间存在几乎线性关系[22],表明在最佳掺杂附近可能存在量子临界行为.但是如图1(a)、(b)所示,在电子型以及等化学价掺杂的情况下,电阻率与温度关系会随着掺杂浓度增加发生明显的变化[19,20]： 首先其室温电阻率随着电子掺杂浓度的上升而不断下降； 其次,电阻率的行为会逐渐从初始的温度线性关系变成温度平方关系,即从非费米液体行为过渡到费米液体行为[23].

“11”型体系的FeSe是目前为止发现的结构最为简单的铁基超导体[24].与其它铁基超导体不同之处在于其正常态没有反铁磁序,但存在结构相变.通过掺杂Te或者S可以压制结构相变[25,26],而中子散射实验表明在Te过量掺杂的样品中存在短程的SDW涨落[27],显示在该体系中磁性与超导电性之间也应该存在密切的关系.

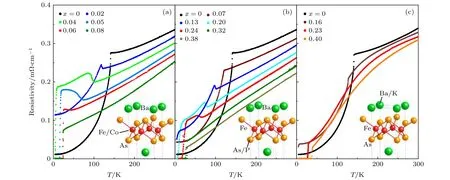
图1 各掺杂浓度下的面内电阻率随温度变化的曲线,分别为以下样品： (a) Ba(Fe1—xCox)2As2,(b) BaFe2(As1—xPx)2,(c) Ba1—xKx Fe2As2[19]Fig.1.Doping evolution of the temperature dependence of the in-plane resistivity for (a) Ba(Fe1—xCox)2As2,(b) BaFe2(As1—xPx)2,and(c) Ba1—xKxFe2As2[19].

从上述这些典型的材料可以看出,在铁基超导体中,磁性和超导电性之间既是竞争关系,同时也存在密切的关联.通过多种掺杂方式可以压制体系中的反铁磁序,从而诱导出超导.此外也可以看到,在掺杂过程中,体系正常态的性质也会发生改变,会伴随出现非费米液体的行为.而在不同体系之间也存在着明显的区别： 在“1111”体系中,表现为从高温的非费米液体行为过渡到低温的费米液体； 但在“122”体系中,只在最佳掺杂附近出现低温下的非费米液体行为.上述两种区别有待进一步的理论解释.作为对比,在空穴型的铜氧化物超导体中,电阻率与温度关系随着掺杂浓度的变化有一个普适性的规律,即在欠掺杂区域,电阻率上存在一个被认为是赝能隙引起的特征温度T∗,在T∗以下电阻率会被压制而偏离线性温度关系； 在最佳掺杂区,则电阻率的线性温度关系会一直延伸到非常低的温度,明显偏离费米液体理论； 到了过掺杂区域,电阻率温度关系逐渐演变为温度平方的费米液体行为.

2.2 各向异性

由于铁基超导体中存在向列相,电阻率在ab面内存在着各向异性.受到可获得的高质量单晶所限制,目前输运性质的各向异性研究主要集中在“122”以及“11”体系.在“122”体系中,不同的掺杂对各向异性有很大的影响.在电子掺杂的“122”体系中,在结构相变温度以上可明显地看到ab面内a方向和b方向的电阻存在着巨大的差异[28,29],该种向列相并非来源于结构相变的结构畸变,而是由电子结构的变化引起.在等位掺杂的EuFe2(As1—xPx)2中进行的扭矩实验也证实在结构相变之上存在向列相[30].而对于空穴掺杂,当掺杂浓度较小时,并未看到明显的各向异性； 随着浓度增大各向异性的符号发生了反转,并且一直保持到低温[31,32].理论计算当位于向列相时由于自旋涨落的存在,导致各向异性的散射,从而引发符号的变化,即表明在向列相的顺磁态中,磁散射占据了主要地位.从上述实验可以看出自旋涨落对铁基超导体正常态性质的重要作用,同时也说明了非常规超导与磁性之间的密切联系.

此外,在“122”体系的 Ba(Fe1—xCox)2As2材料中进行的应力效应实验发现,处于最佳掺杂时,即使施加很小的应力,Tc仍会减小 5倍以上； 随着应力逐渐增大,最后表现为完全的金属态[33],表明向列相的涨落对电子配对的可能作用.但同时发现,Tc与应力之间的关系会随着掺杂而发生改变.在最佳掺杂附近,Tc与拉伸、压缩之间的应力基本呈对称关系.而随着掺杂浓度的增加两者会逐渐变成线性关系,表明可能存在反铁磁序或者涨落的影响,并有待更进一步的研究.至于在“1111”体系中,研究表明在母体中,同样在结构相变之上就发现了各向异性的存在[34],说明向列相也不是由于结构畸变导致的.而在“11”体系的 FeSe 中,各向异性Δρ(T)=ρa-ρb(式中ρa和ρb分别代表沿着互相正交的a方向和b方向的电阻率)与温度之间存在非单调的关系,在结构相变温度Ts以下约20 K达到最大值,并在超导转变温度Tc～ 8.5 K 处变成零[35].理论计算认为,这是由于各向异性的磁涨落的非弹性散射导致的.这些结果都表明磁散射在铁基超导体中的重要性.

3 霍尔系数

铁基超导体母体为补偿型金属(即体系中电子和空穴浓度大小相近,相互补偿),但由于电子的迁移率较大,导致其霍尔系数为负值.在SDW相变温度点附近,霍尔系数(绝对值)会发生急剧增大.而不同类型的掺杂会引入不同的载流子,从而霍尔系数与温度之间的关系也有所不同.在电子型掺杂的情况下,其霍尔系数几乎与温度无关[36,37]； 但在空穴掺杂的情况下,霍尔系数与温度之间存在着强烈的依赖关系.此外,当掺杂浓度达到一定程度后,霍尔系数与温度的依赖关系也会随之发生改变： 霍尔系数从初始的与温度负相关的单调行为,变为在高温处与温度负相关而在低温处与温度正相关的非单调行为,并在“1111”体系中观察到该类行为[12].而在“122”体系的 Ba1—xKxFe2As2中,如图2 所示,当掺杂浓度逐渐接近最佳掺杂x～0.4时,低温的霍尔系数几乎与温度无关[38].

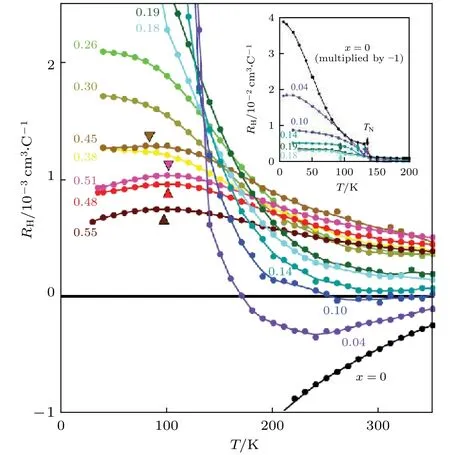
图2 空穴掺杂的“122”体系的霍尔系数随温度的变化[38]Fig.2.The temperature dependence of Hall coefficients for hole-doping “122”-type iron-based superconductors[38].

随着进一步的空穴掺杂,霍尔系数会在高温约100 K附近发生转变,此类行为可能与之前角分辨光电子能谱 (angle resolved photoemission spectroscopy,即ARPES)中观察到的电子结构有关：高温约 90 K 时,在能量分布曲线 (energy distribution curve,即 EDC)上观察到一个鼓包,并在Tc温度以下转变为一个尖峰(即pseudo-peak)[39].该电子结构上的反常行为的出现温度与霍尔系数发生转变的温度接近,同时两者都与mh/me的变化紧密相关.而伴随掺杂浓度的进一步上升,霍尔角的行为从凹形的温度依赖关系变成凸形[40],发生转变时的掺杂浓度大致对应ARPES上观察到的电子型费米面消失的浓度[41],表明霍尔角的变化可能来自于费米面的Lifshitz相变.在等位掺杂的样品中同样也存在一定的异常行为.首先其霍尔系数与温度之间存在强烈的依赖关系,但并未看到空穴掺杂情况中的高温转变现象[23].同时根据能带计算结果,铁基超导体母体为补偿型材料,等位掺杂并不会引入额外的载流子,所以在高场下霍尔系数为RH(H→∞)=1/e(ne-nh),即会有一个巨大的增强.但在高场下的霍尔效应测量表明,其霍尔系数随着磁场是下降的[42],并且在低场时下降更加明显,具体参见文献[42]中的图2.而此类低场的下降现象,会随着掺杂浓度的上升逐渐被抑制.经过数据拟合可以得知其中除了正常霍尔项的贡献之外,还存在奇异金属(strange metal)项的贡献,表明反常金属态在铁基超导体的输运性质中可能存在相当大的影响.综上,霍尔效应强烈的温度依赖关系可能是来自铁基超导体的多带特性,同时也可能存在奇异金属态的贡献.

4 热电势

热电势能够灵敏地探测电子结构的变化,从而反映样品的性质.在铜氧化物超导体中,其热电势在欠掺杂时较大,随着掺杂浓度增加而减小,并在最佳掺杂时几乎为零,其室温热电势值与掺杂浓度之间存在一个经验公式[43,44].相比之下铁基超导材料中却存在巨大的热电势.如图3(a)所示,在电子型掺杂的“1111”体系SmFe1—xCoxAsO中通过对不同掺杂浓度进行热电势的测量可以发现,热电势均为负值,与主要的载流子类型为电子相符.热电势绝对值的大小会随着掺杂浓度的增加先上升再下降,其变化趋势与超导转变温度之间存在一定的类似[45],最大热电势值出现在超导温度最高处.此外如图3(b)可以看出铁基超导体的热电势随着掺杂浓度的变化有两项贡献：S(300 K) =S0(300 K) +S′(300 K).其中第一项代表正常项的贡献,随着掺杂浓度的上升而逐渐上升.而第二项额外的贡献只出现在超导区域,并且表现为与Tc类似的圆屋顶(dome)形状.其与超导转变温度的类似变化表明异常项S′(300 K)与超导之间可能存在紧密的联系,并在Tb1—xThxFeAsO中也看到类似的现象[46].随着掺杂浓度上升,超导温度不断上升,其热电势的大小也不断上升.在x～0.2 时,其热电势达到了108 µV/K,远大于其它铁基超导材料.除了“1111”体系以外,在 Ni掺杂的“122” 体系 BaFe2—xNixAs2中也观测到类似的现象[47].

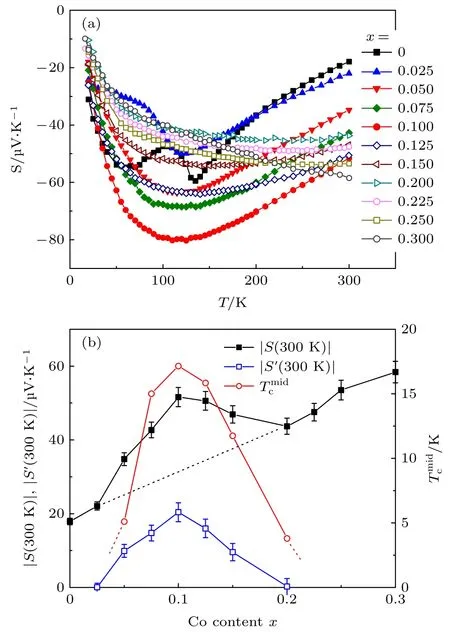
图3 (a) 样品 SmFe1—xCoxAsO 随温度变化的热电势,(b) 热电势绝对值及超导转变温度随掺杂浓度的变化[45]Fig.3.(a) The temperature dependence of Seebeck coefficients for SmFe1—xCoxAsO,(b) Doping dependence of thermopower,|S(300 K)|,|S'(300 K)| and superconducting transition temperature T cmid for SmFe1—xCoxAsO samples[45].

而在“11”体系 FeSe掺杂 Te的样品中,尽管没有看到像“1111”体系这么大的热电势,其热电势绝对值最大值的大小与超导温度之间仍存在类似的关系[48].我们将众多电子型掺杂铁基超导体(包括 LaFeAsO0.9F0.1[49],Ba(Fe1—xNix)2As2[47],SmFe1—xCoxAsO[45],Pr0.8Sr0.2FeAsO[50],FeSe1—x[51],SmFe1—xNixAsO[52],Tb1—xThxFeAsO[46]等材料)的超导温度与热电势绝对值的最大值画在一张图中,如图4所示.尽管个别样品存在较大偏离,但仍能得到两者之间确实存在一定的关联度.这一结果表明在超导温度与热电势之间可能存在一定的联系.

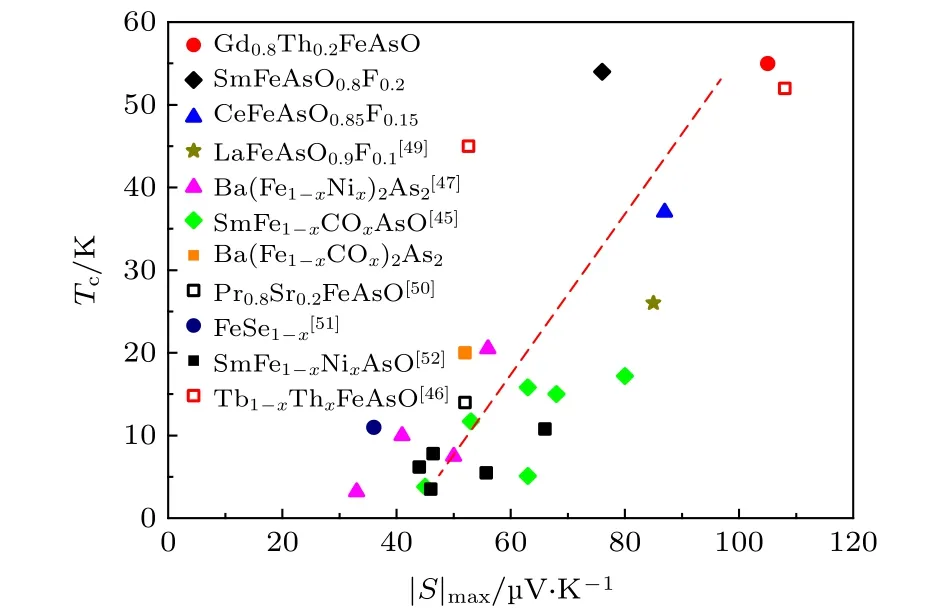
图4 多个体系铁基超导体的热电势最大值与 Tc 之间的关系.图中未加引文的部分为本文作者尚未发表的数据Fig.4.The relation between the maximum of thermopower and the Tc for various iron-based superconductors.The unreferenced portion of the figure is the unpublished data.

但在空穴掺杂的“122”体系中,没有看到类似的现象.在 Sr1—xKxFe2As2和 Ba1—xKxFe2As2中测得的热电势值均为正值,与主要载流子为空穴相符.前者热电势最大值随着掺杂浓度的上升先上升,然后随之下降； 而后者随着掺杂浓度的上升持续下降[53,54].两者在热电势上均未在最佳掺杂附近达到最大值.将Sr1—xKxFe2As2的热电势最大值与掺杂浓度画在一张图中可以得知,在掺杂浓度为0.3(欠掺杂区域)附近会有一个峰出现.同时在掺杂浓度较低时,热电势在SDW转变附近存在一个显著的上升[55],上述的峰可能与SDW序导致了费米面或者态密度发生了巨大的改变有关.这一结果表明在“122”空穴掺杂中热电势的最大值并未出现在Tc最高处的现象可能与SDW序有关,也可能是由于不同的有序态与超导态竞争,而这些有序态对热电势的贡献不同,综合导致了热电势的最大值出现在偏离最佳掺杂处.

此外,为了研究热电势与铁基超导体的FeAs层之间的关系,对LaFeAsO类似的LaNiAsO也进行了热电势的测量[56].LaNiAsO与LaFeAsO结构相似,但不存在结构相变和反铁磁相变,其本身就是超导体,超导温度Tc～2.7 K.通过对其 O 位掺F可以略微提高Tc至3.8 K,仍远低于LaFeAs O1—xFx的Tc.实验得到LaNiAsO的热电势比LaFe AsO小一个量级以上,其更像是载流子浓度较高的良好金属,并显示出常规的费米液体行为.对比两个体系之间在热电势上表现出的巨大区别表明高温超导与FeAs层之间存在着紧密的联系.考虑到铁基超导体为多带体系,以及其热电势大小与Tc之间的联系,表明带间散射可能在高温超导中起到了重要的作用.

铁基超导体中此类巨大的热电势信号可能有以下几种原因： 首先铁基超导体是多带体系,而铜基超导体为单带,由于多带的贡献,导致了铁基超导体的热电势有一个巨大的增强.此外还可能存在其它奇异的低能激发.像NaxCoO2中也存在巨大的热电势,是来自巨大的自旋熵的贡献.而对铁基超导体通过加场下的热电势测量可以得知,SDW相变温度以下的热电势会被磁场压制,但对于SDW转变温度以上磁场对热电势几乎没有影响,并且在SmAsFeO0.8F0.2中反而看到磁场会略微增强正常态的热电势[57],这种行为表明其中并不存在自旋熵的贡献.其中是否存在其它奇异的低能激发的贡献仍有待进一步的实验研究.

5 能斯特效应

与霍尔效应相比,能斯特效应可以更灵敏地探测准粒子的运动信息,并且对超导体中的磁通涡旋运动特别敏感,能反映出非常规超导电性的一些异常行为,比如在铜氧化物超导体中,能斯特效应测量给出了Tc以上较大温度范围内的超导位相型涨落[58].

在正常态下能斯特信号由下述公式决定：ey=ραxy-Stanθ,其中αxy代表非对角佩尔捷系数(off-diagonal Peltier coefficient),S代表热电势,ρ和 t anθ分别代表电阻率及霍尔角.而在Tc附近及以下,能斯特信号由三项组成：ey=+-Stanθ.其中代表磁通运动的贡献,代表正常态元激发的贡献.在超导态,会迅速降为零,而会有一个巨大的峰,其主要体现了超导态的性质,即来自磁通运动的贡献.

对“1111”型铁基超导体 LaO1—xFxFeAs体系的能斯特测量可以看到,在超导临界温度Tc～26 K 以上,能斯特信号为负,与磁场之间为线性关系,符合一般金属的特征,未见超导涨落引起的能斯特效应增大[49].但在超导临界温度之下,能斯特信号增加很快,与磁场之间的关系变成非线性,显示出典型的磁通运动的能斯特信号[49].当T= 10 K 时,磁通线被全部钉扎,能斯特信号几乎为 0.当T=13 K 以及 15 K 时,磁通格子在某一特定磁场下融化,然后磁通开始运动,产生能斯特信号,出现该能斯特信号的磁场对应于磁通格子融化场,即不可逆场.在T＞ 17 K 时,并未观察到磁通格子融化的现象,是由于热涨落已经导致磁通格子不再形成,开始进入磁通液体态.当然,也可能由于多晶样品导致磁通运动的移动不均匀,使得磁通格子融化过程变得模糊.在超导临界温度以下存在一个较大的温度区间,磁通运动的能斯特信号很明显,这点与铜基超导体类似,表明“1111”体系中存在较大的磁通液体区域,磁通线难以被钉扎.造成这一现象的原因,有可能是磁通钉扎太弱,也有可能是二维特性造成磁通格子难以形成,这些需要进一步的探究.此外,从图5(a)能斯特系数与温度之间的关系可以看到,正常态的能斯特信号很小,同时随温度的变化也很小.但是在降温到约50 K时能斯特系数开始增加,并在Tc以上发生符号的改变,随后在Tc处发生了急剧的上升.这种能斯特信号的急剧上升与铜基超导体中观察到的连续缓慢平滑变化存在着明显的区别.在铜基超导体中,这种Tc以上增强的能斯特信号被认为是由于强的超导位相涨落所导致,考虑到铁基超导体与铜基超导体在Tc附近行为显著的差异,说明铁基超导体中超导涨落并不显著.由上所述,正常态的能斯特信号由两部分组成,通过计算可以得知在正常态ey约为Stanθ的 1/5,说明“Sondheimer抵消”[59]并不完全成立.此外αxy在50 K以上随着温度的下降逐渐的上升,在约50 K处达到饱和,表明在约50 K附近电子结构可能发生了改变.由于母体化合物在约134 K附近发生SDW转变,而F掺杂会逐渐抑制SDW转变,所以在超导温度与50 K之间佩尔捷系数的非对角项被异常地抑制可能来自于SDW涨落的影响.在另一个接近的“1111” 体系 NdO1—xFxFeAs中也观察到了类似的现象,能斯特信号持续到超导温度以上约60 K.

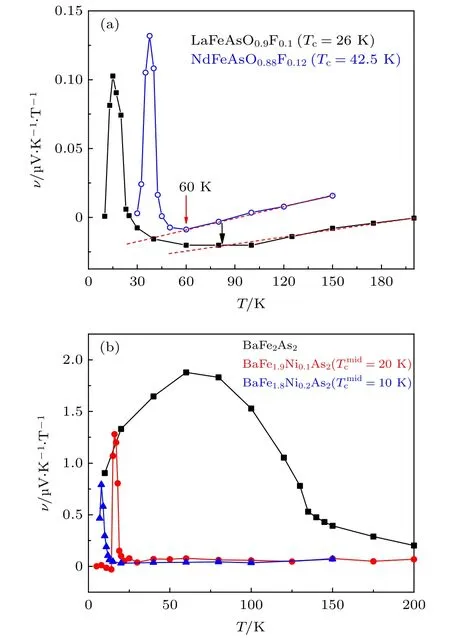
图5 能斯特系数与温度之间的曲线,分别为： (a) “1111”体系[49]； (b) “122”体系中.图中BaFe2As2 的结果与文献 [60]一致Fig.5.The temperature dependence of Nernst coefficients for (a) “1111”-type[49]； (b) “122”-type.The result of BaFe2As2 is consistent with the report in the Ref.[60].

而在“122”体系的 BaFe2—xNixAs2的能斯特实验中,如图5(b)表现出与“1111”体系的显著区别.在Tc以下,当磁场大于某一临界磁场时,磁通开始运动,形成典型的与磁场存在非线性关系的磁通能斯特信号,即对应不可逆场.其与“1111”体系不同之处在于： 磁通运动导致的能斯特信号在超导温度以下仅存在一个很小的温区,并且在超导温度附近的转变更为剧烈； 而在超导温度以上,能斯特信号与磁场之间的关系由原来的非线性行为转变为线性行为,但与温度之间并不存在明显的依赖关系.同样通过对构成正常态的能斯特信号的两个分量进行计算表明,在该温区所谓的“Sondheimer抵消”相对成立,该行为也与“1111”体系中的正常态的反常能斯特信号有所区别.此外,其正常态能斯特信号不为零则来源于背景信号的贡献.上述两个体系在能斯特信号上的显著区别可能来自于其结构上的差异,即“1111”体系表现为二维特性,而“122”体系特性则更趋向三维.

而对铁基超导体母体的能斯特效应测量中,发现其存在巨大的能斯特信号,并且在SDW相变温度时,能斯特信号会发生急剧的改变,但此类改变会随着掺杂浓度的提高很快被抑制.在Eu(Fe1—xCox)2As2中,当x～0.15 时,尽管仍然存在 SDW,但在相变点附近已经没有明显的能斯特信号变化[61].这里能斯特信号的变化与热电势的变化呈现相反的趋势.这类母体特有的巨大能斯特信号可能来自于狄拉克费米子的受限散射,并在母体BaFe2As2的ARPES实验中观察到了狄拉克锥(Dirac cone)的电子色散关系[62],同时在量子振荡实验中也确认存在无质量的狄拉克色散[63].

此外，与“1111”体系结构相类似,对将 FeAs层换为NiAs层的LaNiAsO的能斯特效应的测量发现,其正常态的能斯特信号很小,几乎接近测量背景的噪音量级,并且在6 T左右磁场下其信号大小约比“1111”体系的LaFeAsO小两个量级[56].类似地使用正常态的能斯特公式进行拟合,得到Stanθ与ey变化一致,表明“Sondheimer抵消”部分成立.从上述能斯特效应的研究来看,LaNiAsO更像传统金属,结合之前其在热电势上的对比结果,表明FeAs层及多带效应在铁基高温超导中的重要性.

最近在“11”体系的 Fe1+yTe1—xSex单晶中发现在超导转变温度点附近存在自发的能斯特效应(spontaneous Nernst effect)[64],进一步对扫场的数据进行分析,显示除了通常的关于磁场反对称的能斯特信号之外,还存在与磁场对称关系的能斯特信号.此类对称的能斯特信号可能来自于间隙的Fe原子的局域磁矩导致的强自旋轨道耦合,表明在Fe1+yTe1—xSex单晶中可能存在局域的时间反演对称破缺.上述最新的能斯特效应研究对于理解铁基超导体提供了一个新的角度.

综上,在铁基超导体中存在很大的能斯特信号.母体中的巨大能斯特信号可能来自于狄拉克电子的受限散射.而随着掺杂浓度增加,狄拉克电子态会逐渐消失,导致其掺杂样品的能斯特信号相对母体变小,但此时能斯特信号仍然大于通常金属,这可能来源于铁基超导体的多带特性.此外在结构接近二维的“1111”体系掺杂的正常态中能斯特信号直到60 K高温仍存在异常,但在结构更加三维的“122”掺杂体系并没有在Tc以上看到异常的能斯特信号.这个异常可能是体系的维度降低造成的.这一现象的具体来源有待进一步的研究.而最新的关于“11” 体系的能斯特效应测量表明其中存在关于磁场对称的能斯特信号,反映其可能存在的局域的时间反演对称破缺.

6 可能的量子临界行为

如上所述,铁基超导体在最佳掺杂浓度附近其输运性质上是否存在量子临界行为是一个值得深入研究的问题.电子型“122”体系在最佳掺杂附近的电阻率在低温下表现为线性的温度依赖关系,同时在热电势上S/T与 l nT之间也存在线性关系,其表现形式与量子临界点的特征一致[65].更进一步的NMR实验测得在电子掺杂的BaFe2—xNixAs2中,可能存在两个临界掺杂点,xc1～0.10 以及xc2～0.14,其中前者对应磁性量子临界点,而后者的量子临界点则与结构相变紧密关联[66].在等化学价的掺杂体系 BaFe2As2—xPx中,对x≥0.31 的样品进行测量得到,在欠掺杂区域出现非费米液体行为而在过掺杂区域过渡至费米液体行为,并在最佳掺杂附近其有效质量呈现发散趋势[67],这一点也被高场下的量子振荡实验[68,69]以及穿透深度实验[70]所证实.此外对样品进行磁场下的测量发现,电阻率与磁场之间也是线性的关系,而进一步的对比发现电阻率与磁场及温度之间存在一个标度关系[71],如下述公式所 示 ：式中ρ(H,T) 和ρ(0,0) 分别代表在磁场H和温度T下的电阻率以及零温零场下的电阻率,kB,µB和µ0代表玻尔兹曼常量,玻尔磁子以及真空磁导率,α和γ代表拟合参数.经过拟合可以得到系数γ/α=1.01 ± 0.07,即磁场与温度两者对电阻率的影响接近.进一步的c轴方向电阻率测量实验可得,尽管c方向和ab面之间的电阻率存在着各向异性,但是两者在电阻率的标度行为却几乎一致,可知该行为与电流的方向无关.同时转角测量实验发现,这种标度行为与磁场的方向存在密切关系,只有当磁场垂直FeAs面时才能观察到上述的临界行为[72],此时上述式子中的磁场代表与FeAs面垂直的磁场分量.此类二维性的特征表明FeAs层在铁基超导体中的重要性,并可能与奇异金属行为之间存在一定的联系.而铜基超导体中的奇异金属性也与其强的二维性存在联系,这种关联可能导致它们都出现了与温度线性依赖的电阻率关系.

而在空穴型“122”体系中,最佳掺杂附近电阻率与温度之间存在线性关系[22].并且在热电势上也看到S/T与 l nT之间存在线性关系.在接近最佳掺杂时,100 K 温度以下的S/T与 l nT之间也会随着掺杂浓度接近最佳掺杂而逐渐趋向线性关系,该现象在 Sr1—xKxFe2As2,Ba1—xKxFe2As2[53,54]以及 Eu1—xKxFe2As2[73]中均被观察到.但除了上述的输运性质之外,并未有更进一步的证据表明“122”体系空穴最佳掺杂附近存在量子临界点.此外最近在弹性模量的实验中,并没有在空穴型体系中看到在类似电子型体系中量子临界点导致的一些现象[74].虽然其仍存在电阻与温度的线性行为,但该电阻率通过拟合得到的剩余电阻率为不合理的负值,提示在更低温度下的输运行为还需要更进一步的实验探索,例如在强磁场下的实验,通过抑制超导态来揭示低温下的真实电阻率行为.综上可知空穴型体系中量子临界行为的来源有待更进一步的研究.

7 总结与展望

尽管铁基超导体的发现已经历十余年,对其物理性质的认识也日益深入,但其超导配对机理仍是一个未解的谜团.在铁基超导体中存在的多种有序态,比如电子向列相、电荷密度波、自旋密度波,多种多样的磁有序结构等等,它们与超导电性之间的关系,是否存在量子临界点和临界涨落行为,仍吸引着学者们的极大研究兴趣.输运性质的测量虽是一种相对简单的测量技术,却为认识铁基超导体的低能激发等提供了极为有用的信息.在铜氧化物超导体中,电阻率与温度的关系随着掺杂浓度会出现非常有规律的变化,并在最佳掺杂浓度处呈现非常好的线性电阻率温度关系.而铁基超导体由于其电子结构的多能带特性,使得其电阻率和霍尔系数与温度关系出现多样性的变化,但在正常态并没有看到有赝能隙打开导致的电阻率等输运性质的奇异行为.在空穴型掺杂的铁基超导体中观测到霍尔系数在低温下的变号,电阻率与温度关系上在对应的温区会出现一个很宽的鼓包,甚至在ARPES的EDC谱上相应温度也出现一个反常鼓包,其原因仍不十分清楚.

铁基超导体的热电势行为也表现出与铜氧化物超导体的明显差异.空穴型掺杂的铜氧化物超导体正常态热电势在欠掺杂区很大,到最佳掺杂区变得很小,接近于零,并往往在过掺杂区从正变成负值,寓示着电子结构的变化.在铁基超导体中,正常态热电势的绝对值反而在最佳掺杂区是最大的,并且没有明显的磁场依赖关系.在Tc最高的掺杂浓度区,根据ARPES测量得知的电子结构,此时电子型和空穴型费米面之间存在非常好的叠套(nesting).如此大的热电势值也许跟其电子结构带来的费米面失稳有关.能斯特效应表明铁基超导体的正常态的信号很大,其能斯特系数比一般的金属要大1～2个数量级,如此大的能斯特系数应该来源于多带的电子结构.从超导态到正常态,能斯特信号在Tc处的陡变,表明超导涨落在Tc以上并不明显,这点与铜氧化物超导体存在明显差别.在铁基超导体上所显示的这些反常热电性质,并没有在类似结构的镍基超导体(如LaNiAsO)上观测到,相比之下镍基超导体表现得更像一个通常的金属.上述行为暗示着铁基超导体的这些奇异输运性质与其高温超导电性存在内在的关联,这些因素是建立其超导机理时需要考虑进去的.