图像非广延高斯熵分割的阈值选取方法
2021-01-14聂方彦李建奇张平凤屠添翼
聂方彦,李建奇,张平凤,屠添翼
(1.湖南文理学院洞庭湖生态经济区建设与发展湖南省协同创新中心,湖南 常德 415000;2.湖南文理学院计算机与电气工程学院,湖南 常德 415000)
1 引 言
人类对世界的感知绝大部分是通过眼睛实现的,因此应用机器智能技术实现对客观世界的理解在很大程度上依赖于对输入的图像视频信息的高效处理。图像成像原理及条件复杂多样,要实现对图像的理解并不是件简易的工作。应用图像分割实现对图像目标的分离[1]进而支持图像处理最终功能的实现一直是图像处理领域的底层关键技术。在实践应用中,因图像种类纷繁复杂,因此涌现出来的图像分割技术也层出不穷。考虑到工程实践上的实时性,在很多场所,简洁易实现的阈值化技术得到广泛应用。
图像阈值化的基本原理就是根据图像直方图信息或一些附加信息实现对图像的分割。在生产实践上,目前应用非常广泛的阈值化方法主要有基于统计方差思想的方法(如Otsu提出的非常著名的最大类间方差法[2]及一些改良方法[3-6])、基于信息熵的方法等。统计方差类方法数学机理清晰,算法原理基础扎实,因此在实际应用中得到大范围研究和应用。统计方差类方法有一个出生即存在的不足,即对于不同的统计类,如果类别之间统计量差异很大时,这些方法很容易造成错分,在图像分割上即会存在阈值偏离等现象[4]。信息熵类方法物理意义明确,背靠原理深厚,因此也得到了大量研究和应用,如Kapur提出的最大熵法[7]、Reny熵法[8]、Tsallis熵法[9]及它们的一些变种[10]等。应用信息熵对图像实施阈值分割,方法实现算法简单,性能和效果优异,但是如果图像背景与目标像素分布差异大时,该类方法也极易造成错分。故对于图像分割领域的阈值分割研究来说,这是一个古老的议题,但又历久弥新,现实需求随时挑战着研究人员在该领域的努力和付出。
在实际应用中,很多任务需求图像中的目标与背景像素分布差异大,如工业无损检测中的图像、红外图像[11]等。在该类图像视域中,图像目标像素占整幅图像比例小,目标与背景交融致使边界模糊,在图像直方图上的体现是灰度级分布呈现不规则分布,因此要实现目标的有效分割也不是件容易的工作。在分析传统热力学熵基础上,Frank与Daffertshofer提出一种非广延高斯熵(nonextensive Gaussian entropy,NeG熵)用于处理序贯相关的Ornstein-Uhlenbeck随机过程(OU过程)的非线性Fokker-Planck方程问题[12-14]。在时间序列的推移方向上序贯相关的OU过程将向它的长程均值(long-term mean)方向漂移,该特性与具有长程相关特性的图像具有相似性,因此在这里将NeG熵用于工业无损检测图像及红外图像的分割,并在与其他一些典型方法的比较中考察提出方法的性能。
2 问题描述与算法实现
图像阈值分割是将图像直方图信息作为处理对象,对于两级阈值化来说,就是通过某种特定的工具或方法从图像直方图中找到最合适的一个灰度值作为图像分割的阈值,大于等于该灰度值的图像像素归为一类,小于该灰度值的图像像素归为另一类。假设原始图像坐标(x,y)处的像素值函数为f(x,y),分割后图像该坐标像素值函数为s(x,y),图像像素值域为{0,1,2,…,L-1},设g1、g2分别为两不相等的灰度级值,找到的最佳阈值为t,则图像两级阈值化问题可描述为图像像素的二分类问题,即
(1)
2.1 NeG熵阈值化原理
对于一个完备的概率分布P={p1,…,pi,…,pn},i=1,…,n,p1+…+pi+…+pn=1,Frank与Daffertshofer定义[12]的NeG熵数学表达式为:
(2)
从式(2)可以看出,NeG熵是一个完全与传统信息熵形式不一样的熵表达形式,在该式中,s表示NeG熵指数,s>0且s≠1。为便于观察与计算,采用指数与对数的等价变换,可以将式(2)连乘形式的熵表达式变换为:
(3)
当s→1时,NeG熵收敛于传统Boltzmann-Gibbs熵,即Shannon熵。对于统计独立的概率分布系统P={pi} 和Q={qi},i=1,…,n,NeG熵满足以下形式的非广延可加性原则[14]:
E(P∩Q)=E(P)+E(Q)+(1-s)E(P)E(Q)
(4)
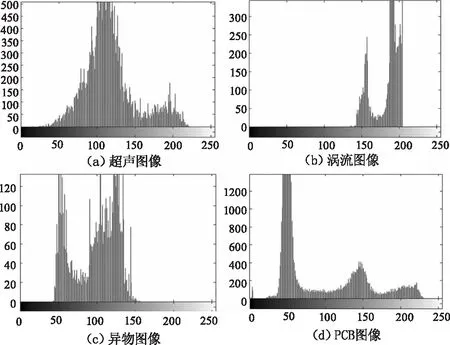
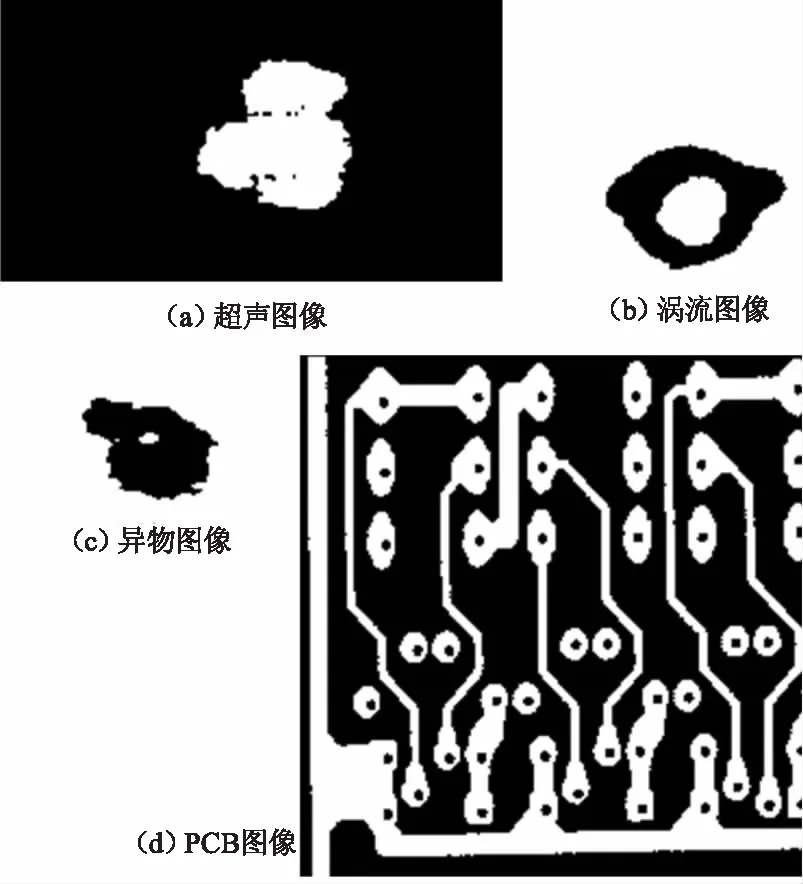
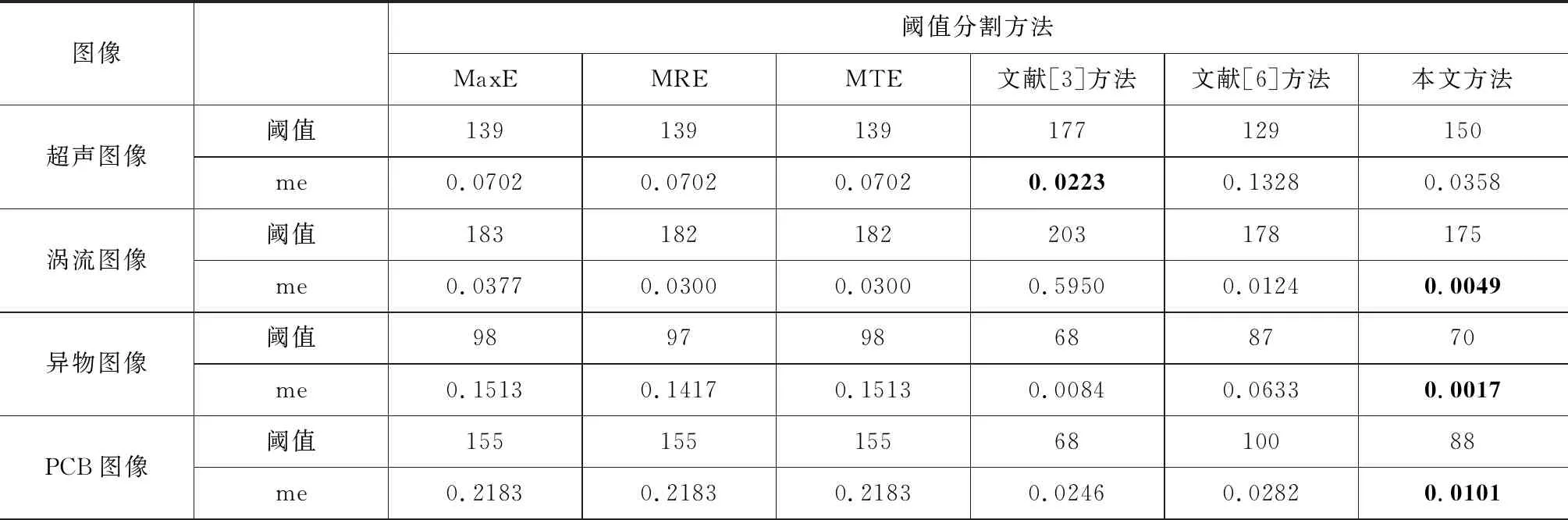
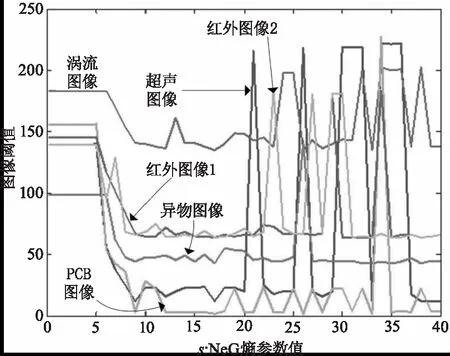
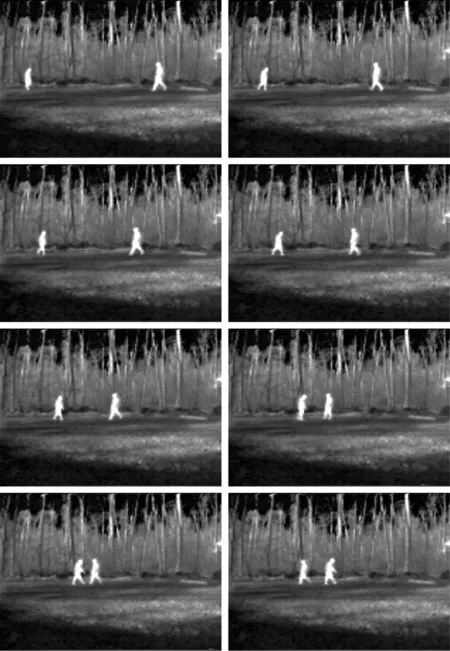
应用NeG熵对图像进行阈值化分割,首先做如下假定。假定待分割图像为I,其大小为m×n,图像灰度级范围为{0,1,2,…,L-1},灰度级的概率分布用图像像素灰度级在图像中出现的频度进行估计,这里图像灰度级的频度hi(i=0,1,2,…,L-1)定义为hi=ni/(m×n),ni表示灰度级i在图像I中出现的像素数量。对待分割图像I进行分割时,假定最佳阈值为t,分割后的两部分分别为图像背景(B)和目标(O),它们对应的灰度级分布概率估计分别为B={bi|0≤i E(I|t)=E(B)+E(O)+(1-s)E(B)E(O) (5) 基于最大熵原则,可据式(5)在图像灰度级G={0,1,2,…,L-1}范围内求取最佳阈值t*,即: (6) 依式(6)计算得出最佳阈值t*后,即可应用式(1)对图像实施分割。 根据以上描述,输入待分割图像后,首先计算图像灰度级直方图信息,然后应用提出的方法对图像实施分割可以得到分割结果,具体来说,该过程可用如图1所示流程图描述。 图1 算法实现流程图Fig.1 The flow chart of algorithm realization 为检验提出方法在对图像实施阈值分割时的有效性,将提出方法在无损检测图像及一些红外图像上进行了实验测试。作为对比,在本节中也将提出方法与基于统计方差思想一些方法及一些熵方法进行了比较。据基于方差思想的文献[3]、[6]描述,这两种方法在对无损检测图像进行分割时能获得较好的效果,因此在这里将这两种方法与本文提出方法进行了比较,为简洁起见,这两种方法在下文中称为文献[3]方法、文献[6]方法。另外,作为广泛应用的Shannon熵方法[7]、Renyi熵方法[8]、Tsallis熵方法[9]是最为经典的熵方法,且它们对图像实施分割的效果也得到了有效检验,因此它们也在这里用来与本文提出方法进行对比,在这里把三种方法简称为MaxE方法、MRE方法、MTE方法。在测试中,相比较的方法都用Matlab(2010a)编码实现,测试机器配置为Intel(R) Core(TM) i7-8550U CPU,16GB内存,64位Windows10操作系统。 为了评判相比较方法的性能,在这里应用客观评价标准像素误分率作为评价准则。图像分割的误分率准则函数在这里定义为: (7) 在测试过程中,首先选用来自文献[15]并在其他文献中得到广泛应用的无损检测图像用于本文相比较各方法的性能评估。图2列出了用于测试的原始无损检测图像,它们分别是一幅超声成像图像(ultrasonic image,超声图像)、涡流成像图像(eddy current image,涡流图像)、材料异物图像(material image,异物图像)以及一幅有缺陷的印刷电路板图像(printed circuit board image,PCB图像),它们的大小分别是232×131、107×92、100×70和232×243。 图2 原始测试图像Fig.2 The original testing images 图3列出的是原始测试图像的灰度级直方图,图4列出的是测试图像文献[15]给出的专家分割结果图像。从图2可以看出,这几幅测试图像背景与目标像素交融,且也可从图3看出,它们的灰度级直方图呈不规则复杂分布,因此要将目标分割出来不是件容易的工作。 图3 原始测试图像灰度级直方图Fig.3 The histogram of testing images 图4 测试图像的专家分割结果Fig.4 The segmented result by experts of testing images 图5~8列出了相比较各方法对原始测试无损检测图像分别进行分割时获得的结果。 图5 超声成像图像的分割结果Fig.5 The segmented results of ultrasonic image 图5列出的是各方法对超声成像无损检测图像的分割结果。从图5可以看出,最大熵法MaxE、MRE、MTE熵法分割后留下的噪声像素点还较多,文献[3]方法有过分割现象发生,文献[6]方法也是留下的噪声像素点过多。本文提出方法获得的结果也有残余噪声点,但如果应用形态学算子进一步处理的话,将会使残余噪声点大幅减少。 图6 涡流图像分割结果Fig.6 The segmented results of eddy current image 从图6~8列出的各方法对涡流图像、材料异物图像以及缺陷印刷电路板图像的分割结果来看,本文方法获得了相比较方法的最好结果。 图7 材料异物图像分割结果Fig.7 The segmented results of material image 图8 缺陷印刷电路板图像分割结果Fig.8 The segmented results of PCB image 以上叙述仅从视觉角度出发对各相比较方法在测试图像上获取的主观分割观察结果。为了更客观的描述各方法的分割性能,以式(7)定义的客观标准为基准,用表1统计了各相比较方法在对各测试无损检测图像进行分割时,获得的最佳分割阈值及分割结果图像与专家分割图像相比存在的像素错分率。从表1可以看出,除了在第一幅测试图像,即超声成像无损检测图像上获得的分割结果像素误分率高于文献[3]方法外,在其他图像的分割上,本文提出方法都获得了相比较方法中最好的分割结果(相比较方法中最低的像素误分率用黑色数字进行了标示)。再比较表1获得的最佳阈值,与图3相比,本文方法获得的最佳阈值也与图像灰度直方图分布的谷点贴合的更紧密。 表1 相比较各方法对测试无损检测图像分割时获得的最佳阈值及像素误分率Tab.1 The thresholds and me values obtained by using different methods for the tested images 为了考察本文方法在其他图像上分割效果,在这里将本方法用于自拍的两幅红外图像的分割。图9列出了这两幅图像及其灰度级直方图,这两幅图像的大小为240×320。从图9可以看出红外图像中人体目标与背景像素灰度级区分不是特别大,除了人体头部等没有被衣服遮盖部分像素值与背景有较大区别外,人体其他部位的成像像素值与背景区分度不大。另外,从这两幅图像的灰度级直方图也可看出,图像像素灰度分布呈现多峰的不规则分布,要找到合适的分隔点将目标提取出来不容易。 图9 红外图像及其直方图Fig.9 Infrared images and their histograms 图10~11列出了相比较的6种方法对这两幅图像的分割结果。从图10~11可以看出,在对这两幅图像的分割中,最大Shannon熵法MaxE、最大Renyi熵法MRE以及最大Tsallis熵法MTE获得的结果图像中目标不完整,人体各部位出现破碎,分割结果对于图像处理后续阶段任务价值不大。而对于基于统计方差思想的文献[3]方法与文献[6]方法来说,在对第一幅红外图像的分割中,两文献提出方法都失败了;对于第二幅红外图像,文献[3]方法完全失败,文献[6]方法获得的结果如果做进一步处理(如形态学算子处理)可以为作为后续阶段任务的基础。本文方法在对这两幅图像的分割中获得的结果优于相比较的各方法获得的结果。 图10 红外图像1分割结果Fig.10 The segmented results of infrared image1 图11 红外图像2分割结果Fig.11 The segmented results of infrared image2 在本文提出方法中,存在着一个可变的NeG熵参数s,该值的改变影响着最佳阈值的获取。图12列出了本文提出方法对各图像进行分割实验时,对参数s取不同的值时获取得到的最佳分割阈值变化曲线图。从图12可以看出,参数s取不同的值对图像阈值分割的最佳阈值获取影响非常大。对于本文测试的6幅图像来说,当0 图12 不同参数s值条件下最佳阈值变化曲线图Fig.12 Threshold change curves on different s values 图12给我们的启示是:通过调校参数s值可使方法具有更好的任务适应性,增强方法的普适程度。对于前文进行的实验涉及的6幅图像,在测试过程中熵参数s取值分别为5.39、7.1、6.3、6.14、6.4及5.9。对于具体的图像分割任务来说,任务场景与成像条件在一定时间和空间范围内是可控的,因此在对图像进行处理时,我们可以先通过一些训练图像找到适合该任务处理的参数s值,然后保持该值对图像实施分割;如果条件发生变化,可以再通过训练来调整参数s的取值。为了证实这一想法的可行性,我们从Terravic Motion IR Database红外图像数据库[16]中的某一序列图像中选取了帧序号为000270,000290,000310,000330,000350,000380,000390,000430的8帧图像开展本实验。这8帧图像的原始图像如图13所示,它们的大小为240×320,图13中图像与帧序号的对应关系是自上到下,自左到右。 图13 序列红外图像样例Fig.13 The samples of a series of infrared images 图14列出了本文方法对图13连续序列帧图像分割的结果。对于这8幅图像,NeG熵参数s统一设置为4。从图14可以看出,对于连续帧序列中的间隔的8幅图像来说,设置统一的参数s值在对图像实施分割时,获得的结果可以将要关注的图像目标分割出来,达到任务处理要求,该实验也验证了前面所描述的想法。可调NeG熵参数s增强了提出方法对任务的普适性,但也增加了参数选择的困难。在本文实验中,所有参数都是通过手工调校达到要求,对于怎样自适应地找到合适参数值,也是后续工作需要考虑和研究的问题。 对于相比较的6种方法,各方法的算法时间复杂度都为O(L),其中L为图像灰度级数,对于8位数字图像来说,L=256。所以这些方法在对图像实施分割时都能获得较好实时性能。 相对于本文实验环境,以图13中240×320大小的红外图像为例,本文提出算法处理时间约为0.03 s,也即30 ms左右,对于实践图像处理任务来说,是可以保证实时性处理需求的。 图14 图13图像分割结果Fig.14 The segmented results of images inFig.13 对于当前各种智能或智慧业务来说,图像处理一直是其中的底层关键支撑技术。在图像处理中应用分割算法实现图像目标的提取是更为底层的关键操作。本文讨论并提出了应用非广延高斯熵实现图像阈值分割的方法。该方法充分利用NeG熵处理图像灰度级概率分布长程相关、不均衡、非规则等特性的能力,实现对图像的有效分割。在方法构建及论证过程中,以各类不同成像机理的无损检测图像以及红外图像为例,验证了提出方法的有效性及在工业实践中应用推广的可能性。2.2 算法实现流程图
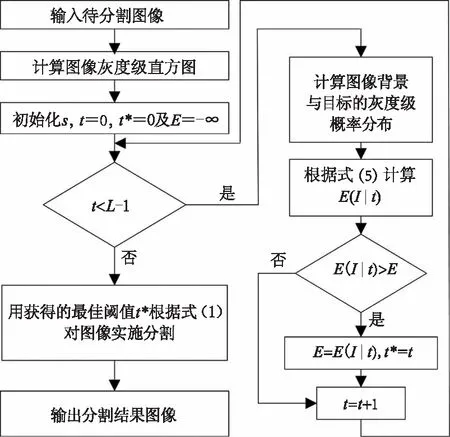
3 实验与结果分析
3.1 性能评估





3.2 红外图像分割实验



3.3 参数s对最佳阈值获取的影响
3.4 时间性能

4 结 论
