基于自适应多子直方图均衡的图像增强算法

苑豪杰， 刘昌禄， 许建平， 胡敬营

(江苏自动化研究所， 江苏 连云港 222061)

基于自适应多子直方图均衡的图像增强算法

苑豪杰， 刘昌禄， 许建平， 胡敬营

(江苏自动化研究所， 江苏 连云港 222061)

传统的直方图均衡算法存在一些缺陷,如局部过增强现象和增大图像噪声。针对这些缺陷,提出了自适应多子直方图均衡算法,该算法首先对原始图像的直方图进行分割,接着对子直方图的灰度级进行重新映射,然后重新分割映射后的直方图,调整直方图中灰度级的频率,最后分别对各个子直方图进行均衡处理。实验表明,该算法能够在对图像进行增强的基础上,有效地降低了过增强的影响,同时在保持图像细节方面有比较好的表现。

图像增强; 直方图均衡; 子直方图; 灰度级

刘昌禄(1963-)，男，研究员。

许建平(1960-)，男，高级工程师。

胡敬营(1979-)，男，高级工程师。

图像增强就是采用某种技术手段来改善图像的视觉效果,或将图像转换成更适合人眼观察和机器分析识别的形式,以便从图像中获取有用的信息。目前,已经有许多针对图像增强的算法,其中，直方图均衡算法(Histogram Equalization,HE)由于在软件中计算简单并且易于在商用硬件上实现,已经成为图像增强处理的一种流行工具[1]。它通过原始图像的累积分布函数来拉伸图像灰度级的动态范围,进而改变图像的对比度,达到图像增强的目的。然而,直方图均衡具有一些缺陷,比如它会显著改变原始图像的亮度,使图像高频灰度级区域出现过增强的现象;对低频灰度级增强不明显,甚至出现灰度级合并的现象。

为了克服传统直方图均衡的缺陷,许多学者提出了改进的直方图均衡算法。一般来说这些算法主要可以分为三类:第一类算法是分割直方图均衡,主要包括保持图像亮度均值的双直方图均衡算法(BBHE)[2]、双子图像直方图均衡算法(DSIHE)[3]、最小均值亮度误差双直方图均衡算法(MMBEBHE)[4]、迭代均值分割直方图均衡算法(RMSHE)[5]、迭代子图像直方图均衡(RSIHE)[6]、基于灰度均值保持的峰值剪切直方图均衡算法(BHEPL)[7]以及基于亮度保持的加权平均多峰直方图均衡算法(WAMSHE)[8]等,在低对比度的图像中,这类算法能较好地保持图像的亮度,但却不能突出图像的细节;第二类算法是动态分割直方图均衡,主要包括动态直方图均衡(DHE)[9]、基于亮度保持的动态直方图均衡(BPDHE)[10]以及象限动态直方图均衡化(QDHE)[11],这类算法能够较好地突出图像的细节,但是不能控制图像增强的程度;第三类算法是基于人类视觉的直方图均衡算法,主要包括基于视觉对比度增强的直方图均衡算法(VCEAHE)[12]以及基于灰度间隙调整的对比度增强直方图均衡算法(CEGAHE)[13],这类算法能达到较好的图像增强效果,但是实现起来比较复杂,不利于算法的硬件实现。

以上改进的直方图均衡算法都可以在一定程度上克服传统直方图均衡的缺陷,但是又会引进其他的问题,比如增强程度不易控制、图像细节表现不稳定。本文在以上算法的基础上提出了自适应多子直方图均衡算法(Adaptive Multi Sub-Histogram Equalization,AMSHE),该算法的自适应性主要体现在两个方面：一是可以自适应地调整子直方图的灰度级动态范围,二是可以自适应地调整各灰度级的频率。实验结果表明,本文提出的算法达到了预期的效果。

1 直方图均衡算法

直方图均衡可以将具有任意分布规律直方图的原始图像变换为具有均匀分布直方图的图像。因此,直方图均衡可以增加像素灰度值的动态范围,使每一灰度级所占的像素个数尽量均等,从而改善图像的整体对比度[8]。

对于数字图像,其直方图均衡化处理的计算过程如下:

1)计算原始图像灰度级的概率密度函数

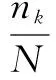
(1)

其中,l是原始图像灰度级,nk是原始图像中第k级灰度级对应的像素数量,N是像素总数,L为图像的灰度级总数。

2) 利用概率密度函数计算原始图像的累积分布函数。

(2)

3) 确定直方图均衡的映射函数,建立原始图像与输出图像灰度级的对应关系。

f(k)=(L-1)c(k)

(3)

2 自适应多子直方图均衡算法

针对图像增强程度不易控制,图像细节表现不稳定等问题,本文提出了自适应多子直方图均衡算法,该算法分为五部分:1)对原始图像的直方图进行分割;2)调整子直方图灰度级的动态范围;3)调整各灰度级的频率;4)归一化累积分布函数;5)对子直方图分别进行直方图均衡。各部分详述如下:

1) 直方图分割

首先利用直方图的灰度中值对原始图像的直方图进行分割,再利用各子直方图的灰度中值对子直方图再一次分割,即迭代地分割两次(r=2),把原始图像直方图分割成4 (2r,r=2)个子直方图。之所以选择分割数目为4,是因为分割数目越多,不仅造成图像处理过程更复杂,还会使分割对图像处理的作用变小,比较极端的例子是分割数目和图像灰度级总数一样时,就相当于对每个灰度级单独处理,即和没有分割的情况一样;当分割数目为2时,也就是BBHE算法和DSIHE算法的情况,分割的效果并不是太好。为了取得较好的图像处理效果,本文的分割数目选为4。分割之后,每个子直方图中相对应的像素数量大致相等,这样调整灰度级动态范围时可以取得较好的效果。分割过程示意图如图1所示,图中m0和m4分别为原始图像灰度值的最小值和最大值。

图1 原始直方图

2) 动态范围调整

在步骤1)中,利用原始图像灰度级中值把原始图像的直方图分割成4个子直方图,其灰度级区间分别是[m0，m1]、[m1，m2]、[m2，m3]和[m3，m4],由图1可知,某些子直方图中像素总数Mi与灰度级范围的比值比较大,如果直接对子直方图进行均衡,容易造成灰度级合并,导致图像中某些细节信息的丢失,造成图像的增强效果相对较差[8]。因此,在对子直方图进行均衡之前,对子直方图的动态范围进行调整。调整过程如下:

spani=mi-mi-1+1

(4)

(5)

aspani=spani+α*(r-spani)

(6)

式中,spank为子直方图灰度级动态范围,k为子直方图数目,α为子直方图动态范围的调整因子,aspank为调整后的子直方图灰度级动态范围。

子直方图灰度级动态范围调整之后,重新映射到整个灰度级上,从而拉伸了图像的灰度级范围,减小了灰度级合并的发生。调整的结果如图2所示。

图2 灰度级重新映射示意图

3) 灰度级频率调整

直方图均衡无法控制图像增强的程度,因此常常出现过增强的现象。本文通过在AMSHE算法中引入图像增强程度的控制因子β,从而能够自适应地控制图像增强的程度。为了简化运算,本文把灰度级范围重新调整的直方图按灰度均值分割成两个直方图进行处理。

Yang.S曾在BUBO算法[14]中提出了通过设定一个上界和一个下界把原始图像的概率密度函数限制在某一个范围内的方法,但是这样会造成与被限制概率密度函数相对应的累积分布函数呈线性增长,降低相关区域的图像增强效果。为了克服BUBO算法的这个缺点,本文按如下的方式调整灰度级的概率密度函数。

(7)

式中,pmin,pmax和pmid分别为原始图像灰度级概率的最小值、最大值以及二者的平均值。控制因子β的确定方式如下:

(8)

式中,Xm,Xml和Xmu分别为原始图像的灰度级均值、两个子直方图的灰度级均值,计算方式如下。

(9)

(10)

(11)

调整前和调整后的原始图像灰度级概率密度函数示意图如图3和图4所示。从图中可以看出,修改后的概率密度函数曲线更加平滑,这意味着灰度级频率调整之后,各灰度级的频率分布更加均衡,从而可以避免直方图均衡处理之后的图像出现过增强现象。

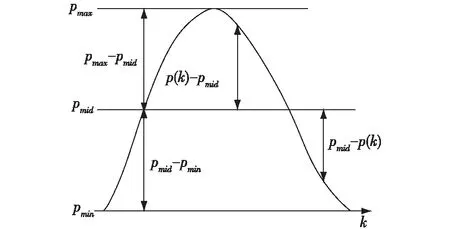
图3 修改前概率密度函数示意图

图4 修改后概率密度函数示意图

4)累积分布函数归一化

概率密度函数经过人为调整之后,

(12)

所以,需要对累积分布函数进行归一化处理,处理方式如下:

(13)

(14)

5)直方图均衡

确定了新的累积分布函数就可以分别对各个子直方图进行均衡化处理了,具体过程与传统的直方图均衡类似,在此不赘述。

3 实验结果及分析

本文的实验在Matlab R2012a上完成。下面通过三组实验结果来对比几种比较经典的算法与本文算法的输出图像在主观上和客观上的优劣。

根据这三组实验结果可以看出,原始图像经过传统的直方图均衡算法处理后,输出图像会出现非常明显的过增强现象;以DSIHE算法和BHEPL算法为代表的分割直方图均衡算法能较好地保持图像的亮度,当处理对比度较低且较暗的图像,无法很好地处理图像的细节;以DHE算法、BPDHE算法以及QDHE算法为代表的动态分割直方图算法能比较好地显示图像的细节,但是有时会出现过增强现象;而本文算法不仅能有效抑制输出图像的过增强现象,而且没有在图像中引入噪声,主观上整体视觉效果较好。

图5 第一组实验结果

图6 第二组实验结果

图7 第三组实验结果

前文从主观视觉效果上比较了各算法的优劣,下面引入图像的信息熵(entropy)从客观上将本文提出的AMSHE算法与几种经典的算法进行比较。信息熵的定义如下:

(15)

图像的信息熵反映了图像中平均信息量的多少,信息熵越大说明图像包含的信息越丰富,因此它可以被用来作为评价图像的量化标准。三组实验中各图像的信息熵如表1所示。由表1可知,本文AMSHE算法的输出图像的信息熵最大,这说明AMSHE算法在保持图像细节方面有比较好的表现。

综合以上可以看出,本文提出的AMSHE算法无论是在主观上还是在客观上都取得了比较好的图像增强效果。

表1 各输出图像的信息熵

4 结束语

本文针对传统直方图均衡算法的缺点,比如容易出现过增强现象、图像细节表现不稳定等,提出了一种自适应多子直方图均衡算法。与几种比较经典的直方图均衡算法相比,本文提出的算法能够在对图像进行增强的基础上,有效地降低了过增强的影响,同时在保持图像细节方面有比较好的表现。实验表明,无论是主观上的视觉效果,还是客观上的信息熵,本文提出的算法均优于经典的直方图均衡算法。

[1] Rafael C.Gonzalez,Richard E.Woods.数字图像处理[M].阮秋琦,等译.第3版.北京:电子工业出版社,2012：72-88.

[2] Yeong-Taeg Kin.Contrast enhancement using brightness preserving bi-histogram equalization[J].IEEE Tans on Consumer Electronics,1997,43(1):1-8.

[3] Yu Wang,Qian Chen,Baomin Zhang.Image enhancement based on equal area dualistic sub-image histogram equalization method[J].IEEE Trans on Consumer Electron,1999,45(1):68-75.

[4] Soong-Der Chen,Abd Rahman Ramli.Minimum mean brightness error bi-histogram equalization in contrast enhancement[J].IEEE Trans on Consumer Electronics.2003,49(4): 1310-1319.

[5] K.S.Sim,C.P.Tso,Y.Y.Tan.Recursive sub-image histogram equalization applied to grayscale images[J].Pattern RecognitionLetters,2007,28(10):1209-1221.

[6] Soong-Der Chen,Abd Rahman Ramli.Contrast Enhancement using Recursive Mean-Separate Histogram Equalization for Scalable Brightness Preservation[J].IEEE Transactions on Consumer Electronics,2008,49(10): 1301-1309.

[7] Chen Hee Ooi,Nicholas Sia Pik Kong,Haidi Ibrahim.Bi-histogram with a plateau limit for digital image enhancement[J].IEEE Trans on Consumer Electronics,2012,55(4): 2072-2080.

[8] Mohd.Farhan Khan,Ekram Khan,Z.A.Abbasi.Weighted average multi segment histogram equalization for brightness preserving contrast enhancement[C].Proceedings of IEEE International Conference on Signal Processing,Computing and Control.2013:1-6.

[9] M.Abdullah-Al-Wadud,Md.Hasanul Kabir,M.Ali Akber Dewan,Oksam Chae.A dynamic histogram equalization for image contrast enhancement.IEEE Trans on Consumer Electronics[J].2007,53(2): 593-600.

[10] Haidi Ibrahim,Nicholas Sia Pik Kong.Brightness preserving dynamic histogram equalization for image contrast enhancement[J].IEEE Trans on Consumer Electronics.2012,53(4): 1752-1758.

[11] Chen Hee Ooi,Nor Ashidi Mat Isa.Quadrants Dynamic Histogram Equalization for Contrast Enhancement[M].IEEE Press,2010.

[12] Chih Chung Ting,Bing Fei Wu.Visual Contrast Enhancement Algorithm Based on Histogram Equalization[J].Sensors.2015,15(7)：16981-16999.

[13] Chung Cheng Chiu,Chih Chung Ting.Contrast Enhancement Algorithm Based on Gap Adjustment for Histogram Equalization[J].Sensors.2016,16(6)：936-954.

[14] Yang S,Park Y.Contrast Enhancement Using Histogram Equalization with Bin Underflow and Bin Overflow[J].International Conference on Image Processing,2003：881-884.

Image Enhancement Algorithm Based on AdaptiveMulti Sub-histogram Equalization

YUAN Hao-jie,LIU Chang-lu,XU Jian-ping,HU Jing-ying

(Jiangsu Automation Research Institute,Lianyungang 222061,China)

Conventional histogram equalization has some shortcomings,such as increasing image noise and local excessive enhancement.To overcome such shortcomings,this paper proposes an image enhancement algorithm based on adaptive multi sub-histogram equalization.Firstly,divide the histogram of original image into four sub-histogram; then,remap the gray level of each sub-histogram; next,divide the histogram once again and adjust the frequency of the gray level in the sub-histograms; finally,the histogram equalization is implemented to each sub-histogram.Simulation results indicate that the improved algorithm not only can reduce the effect of local excessive enhancement,but also preserve the details of the original image.

image enhancement; histogram equalization; sub-histogram; gray level

TP391.41；E917

A

10.3969/j.issn.1673-3819.2017.05.010

1673-3819(2017)05-0045-05

2017-06-29

2017-08-13

苑豪杰(1990-),男,河南周口人,硕士研究生,研究方向图像增强。