麻山药种植田沙壤土流动性离散元模型颗粒放尺效应
2021-01-14郝建军龙思放李建昌马志凯赵晓顺赵建国
郝建军,龙思放,李建昌,马志凯,赵晓顺,赵建国,李 浩
麻山药种植田沙壤土流动性离散元模型颗粒放尺效应
郝建军,龙思放,李建昌,马志凯,赵晓顺,赵建国,李 浩
(河北农业大学机电工程学院,保定 071000)
为简化麻山药-沙壤土复合体离散元模型,提高离散单元法在农业领域中的计算效率,以沙壤土为研究对象,在EDEM离散元软件中构建非球形颗粒,进行双目标参数标定试验,采用放大颗粒粒径方法,利用转鼓、坍塌与FT4流变仿真试验,从颗粒群动态堆积角、流动质量、流动速率以及能量等方面探究了颗粒放尺效应对颗粒群物理特性的影响。试验结果表明:干燥处理后的2 mm粒径沙壤土基质静态堆积角和动态堆积角平均值分别为32.16°和35.02°;与独立标定试验相比,双目标标定试验获得的仿真参数更具准确性与唯一性;在动态堆积角试验中,真实沙壤土颗粒在转鼓中所形成的动态堆积角随粒径和旋转速度的增大而减小,而在仿真试验中,转鼓转速相同情况下,非球形颗粒群在增大粒径的情况下所产生的动态休止角差异较小;坍塌试验中,不同粒径颗粒群在流动过程中的流动质量与平均流速变化趋势基本一致,但误差随粒径增大而增大;颗粒质量相同时,将粒径分别放大2倍及4倍,颗粒数量同比减少87.24%、98.92%,仿真时间明显缩短,计算效率显著提高;FT4流变试验表明,当放尺因子为2时,阻力F及其力矩随时间变化的拟合曲线值约为原尺时的2倍,而当放尺因子为4时,与原尺相比,拟合曲线斜率差异显著,相关性明显降低。研究结果可为构建沙壤土离散元放尺模型提供理论依据,同时也可为农业工程离散元放尺仿真计算提供一定参考。
土壤;模型;颗粒放尺;沙壤土流动特性;标定试验
0 引 言
离散单元法(Discrete Element Method, DEM)通常用于农业物料研究领域[1-5]。但在较大规模的农业、工业应用中,由于高量级的颗粒数目与计算性能的限制[6-9],无法在物理尺寸上对粒子进行1:1的建模[10],制约了其在农业领域的广泛使用。通常,麻山药种植在黏度较小、流动性较强的沙壤土中,扎根一般在地表以下0.6~1.2 m,甚至深达1.5 m,机收时动土量大,且极易划伤或折断。为实现麻山药高效低损机械化收获,很有必要对机收过程进行数值模拟研究,为麻山药收获机械设计提供参考。但建立麻山药-沙壤土离散元复合模型颗粒数量在百万至千万量级,仿真效率低。因此,开展颗粒放尺流动性效应研究对麻山药收获机械的设计具有重要意义。
Thomas等[11]在保持几何体尺寸不变的同时,通过人为的忽略颗粒尺寸小于某个值的粒子[12-13],从而减少模型中的颗粒总数,此方法中的颗粒并不是真实粒子的表示,被称为具有代表性的离散体积元素[14-16]。Grima等[17]将煤料离散元颗粒模型的直径按比例放大4倍,对排料时间变化进行了研究,结果表明,可以准确预测排料时间,误差在10%以内。Xie等[18]将颗粒粒径放大2倍后模拟输料过程中管道内壁的磨损情况,结果表明放尺之后仍然可以准确预测实际磨损状况,但进一步放尺会增大结果误差;Grima等[19]对颗粒材料离散元模型在输送过程中对冲击板所产生的力进行了数值分析,结果表明,当离散元颗粒模型尺寸扩大23%时,与原尺寸相比,受力值无显著变化;但若将颗粒离散元模型半径放大2~3倍,结果与原尺寸相比偏差较大。李毓等[20]对粗粒原型土进行缩尺,并根据级配试验结果推测原型土的力学参数,结果表明:颗粒缩尺后土体的级配变化与土体抗剪强度之间具有较好的曲线关系,证明了将颗粒离散元模型进行缩尺研究的可行性。由此可见,针对不同工况,在一定范围内对颗粒进行放尺或缩尺操作是可行的。因此,本文基于EDEM软件,探究颗粒放尺对沙壤土颗粒流动特性的影响,旨在为减小仿真计算量、提高仿真效率以及构建麻山药离散元收获放尺模型提供理论依据。
1 试验设计
1.1 试验思路
仿真参数校准方法一般包括直接测量法与参数批量校准。直接测量法是通过设计与所测参数直接关联的重复试验,得到较为准确的参数值,例如通过碰撞测定试验来获取碰撞恢复系数值,通过滑板试验来确定静摩擦因数等。直接测量法得到的参数具有准确的物理意义,但并不能保证精确测量得到的微观性能值能够准确预测出颗粒群的整体特性,一些情况下测得的值甚至与软件本身运行代码无关;与此同时如果颗粒尺寸相对较小或形状不规则,则会增加测量试验的难度,从而影响到测量精度。参数批量校准是以颗粒群的一种或多种物理特性作为响应目标,通过在离散元软件中重复该试验并不断调整多个较为显著的仿真参数,从而达到与实际试验中颗粒群特性相一致的效果,标定程序即结束。相比于直接测量法,该方法所得参数的物理意义会有不同程度上的失真,颗粒群的整体响应可能受更多参数的影响,并且只有进行两个或多个独立标定试验才可能获得唯一解,由此可见,该方法存在一定局限性[21]。但当颗粒粒径被放大后,整个颗粒群系统中的总自由度减少,同时颗粒群的整体响应取决于粒子间交互关系的总和,能否使用原尺的参数值还是一个未知数。在这种情况下,使用直接测量法不太恰当,相反将参数批量校准与粒径缩放一起使用效果会更好。在EDEM软件中,瑞丽时间步长T计算公式如试(1)
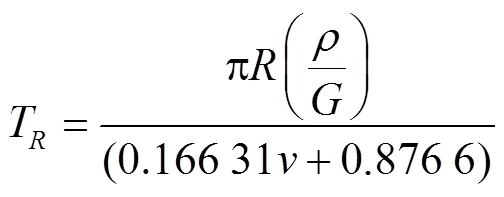
式中表示最小颗粒半径,m;表示颗粒密度,kg/m3;表示颗粒弹性模量,MPa;表示颗粒泊松比。
由式(1)可知,在相同计算域内,增大颗粒半径不仅可以减少颗粒数量,而且还可增长仿真计算时间步长,有利于提高仿真效率。
1.2 沙壤土基质模型构建
以河北省安平县种植麻山药的沙壤土为研究对象。本文重点研究颗粒放尺效应,由于有关含水率颗粒间接触模型理论基础尚不完善,且参数标定是以颗粒群整体特性作为响应目标,对去除石块后的沙壤土进行烘干处理(8 h,108 ℃)可以避免因接触模型带来的理论误差。随后结合本课题组基于2 mm土壤粒径的研究结果[1],按照2倍递增的关系对颗粒模型放大进行研究,又因转鼓尺寸限制将最大粒径定位8 mm(如若进一步使用粒径更大的颗粒,颗粒群层流效果不明显,同时颗粒离散程度较大,会导致试验与结果测量误差较大),故分别使用孔径为2、4、8 mm的专用土壤筛进行筛分,形成3组不同粒径的颗粒群(如图1)。
球形度越低,颗粒内部间的互锁效应越强、颗粒群的流动性越弱。若在EDEM软件中使用单球面颗粒,无疑要通过增加静摩擦因数与滚动摩擦系数来补偿颗粒间的互锁效应,因此颗粒形状对于动态堆积角试验影响尤为重要。由于种植麻山药前,沙壤土是经过深旋(约1.5 m)作业,土壤破碎程度高、结块情况较少、土质较为均一,且在仿真试验中无法对实际土壤颗粒群中的每一个单独颗粒基质进行外观建模,因此该试验中的颗粒处理方法参照Thomas等[11],对常见核状、角状、块状及条状4种典型土壤基质外形进行3~4球面填充建模[2],忽略小于筛孔孔径的颗粒尺寸,并将所有颗粒粒径统一认定为孔径尺寸,仿真颗粒粒径分别设定为:2、4、8 mm,采用EDEM软件中的Hertz-Mindlin(no slip)模型作为土基质间的接触模型,颗粒形状如图2所示。
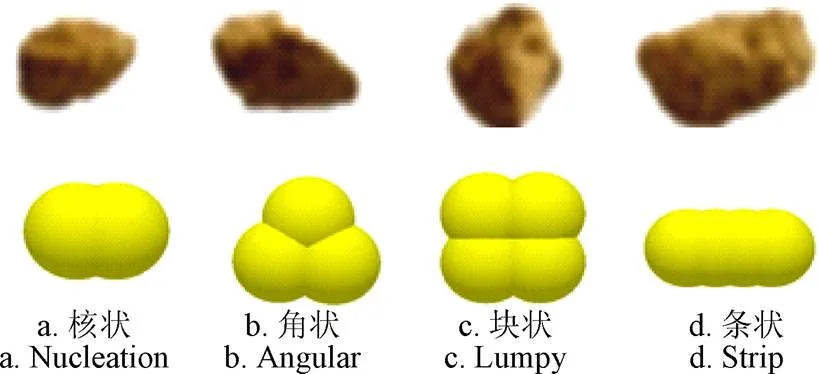
图2 颗粒填充模型
1.3 试验方法
首先采用静态堆积角试验[1]获得了粒径小于2 mm沙壤土基质群的静态堆积角度平均值为32.16°,在EDEM软件中的GEMM材料数据库中,输入静态堆积角度,共得到10组组合参数(如表1所示),其中3组表面能为0,符合试验条件;其次,利用转鼓动态堆积角筛选试验(粒径2 mm,转速4 r/min),获得动态堆积角依次为31.11°、27.31°、33.09°。而实际试验获得2mm沙壤土基质群的平均动态堆积角为35.02°,第3组参数最为接近,但误差较大(5.51%)。为减小试验误差,进一步采用静态堆积与动态堆积2个独立试验进行标定。颗粒间静摩擦因数与滚动摩擦因数对颗粒群所形成的静态堆积角度及动态堆积角度影响最大[22-25]。因此,利用响应曲面法对上述两因数进行双目标标定试验,其他参数值沿用GEMM材料数据库中参数值;随后,使用标定得到的仿真参数进行动态堆积角颗粒放尺仿真试验,并将实际试验与仿真结果进行比对,从颗粒群堆积特征定性分析放尺效应。进行坍塌与FT4流变仿真试验,分别将颗粒群流量以及流变仪叶轮叶片所受到的阻力、转矩作为观察值,定量分析放尺操作对颗粒群流动效应的影响。
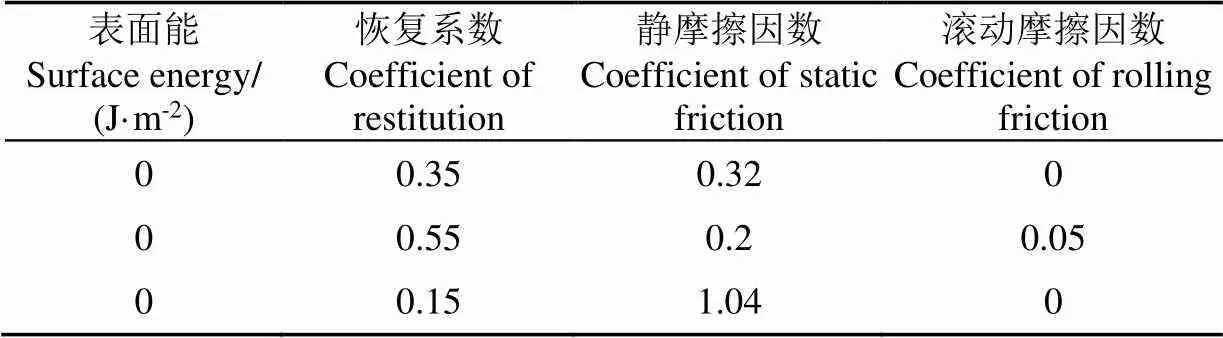
表1 静态堆积角试验筛选结果
1.3.1 转鼓试验
整个转鼓试验装置包括转鼓、电机(LCMT-04L02-60M013-30DC)、24V/200W直流伺服电机驱动器和计算机,驱动器通过LCDA806H调试软件利用上位机进行驱动器参数设置,进入内部速度模式调节转鼓转速,试验装置如图3a所示。转鼓厚=25 mm,半径=75 mm,转速分别设定为4、40、80 r/min[22],转鼓尺寸及动态堆积角测量方法如图3b所示。在预试验中,为便于试验动态堆积角度的观察,在转鼓中盛放土壤占整个转鼓空间的50%左右(土壤质量约为40 g)。

图3 转鼓试验
根据式(2)可预测转鼓中颗粒群的运动特征:
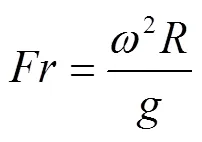
式中表示摩擦系数;表示转鼓半径,m;表示转鼓转动角速度,rad/s;表示重力加速度,m/s2。本装置得到当转速为4 r/min时,=1.48×10-3且满足填充率大于10%,根据梅尔曼准则[26],10-4<<10-2,颗粒群的运动特征可以确定为滚动;当转速为40、80 r/min时,=1.48×10-2、=2.96×10-2,10-3<<10-1,颗粒群的运动出现层流及倾泻现象。
1.3.2 坍塌试验
坍塌仿真试验原理如图4所示。参考Coetzee[21]相关研究方法,该装置宽度=140 mm,厚度=40 mm,落料口径=40 mm,落料高度=80 mm,导流板倾斜角度=45°。在EDEM软件中落料口出设置一平板,待颗粒填充完毕,将该平板设置为虚拟,实现落料过程。另在落料出口正下方添加一个40 mm×40 mm×20 mm的方形流量传感器,以获取颗粒流量信息,分析不同尺寸颗粒群在流动过程中的差异。
1.3.3 FT4流变试验
FT4流变仿真试验原理如图5所示。在该装置中,叶片以40 mm/s的前进速度、60 r/min的旋转速度进入圆柱形颗粒床,此螺旋运动方式会使颗粒产生复杂的应力和流动状态,近似于动态系统(例如旋耕机和振动筛分机械)中引发的颗粒运动条件[27]。
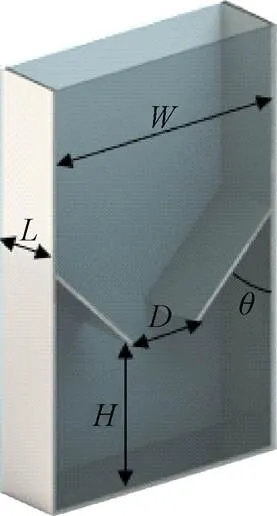
注:W表示装置宽度,mm;L表示装置厚度,mm;D落料口径,mm;θ为导流板倾斜角度,(°)。
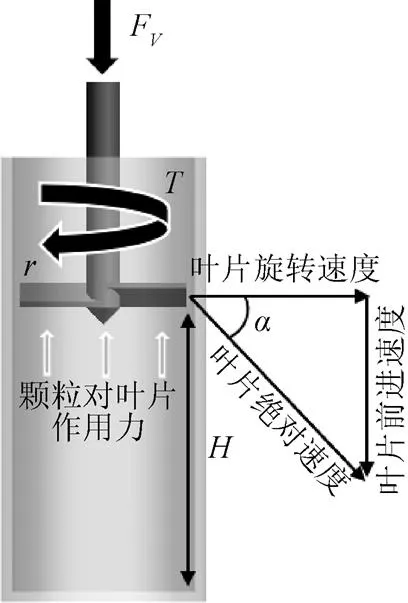
注:H表示旋入颗粒床深度,mm;FV表示叶片前进方向所受到反作用力,N;T表示转矩,N·m;r表示叶片半径,m;α表示叶片尖端运动速度与水平方向所成夹角角度,m·s-1。
通过测量颗粒材料对叶轮叶片产生的阻力F和转矩,计算叶轮叶片所需功耗,作为颗粒材料流动性指标,计算公式如下:
2 试验过程与结果分析
2.1 试验过程
以筛分好的不同粒径土壤颗粒为对象,在不同转速下进行动态堆积角试验,试验结果如表2所示。通过双目标标定试验,探究静摩擦因数()与滚动摩擦因数()对静态(1)、动态堆积角(2)的影响,为动态堆积角对照仿真试验提供仿真参数。因素编码值与仿真试验结果如表3所示,使用State-East公司的Design-Expert V8.0.6.1软件对试验数据进行响应面分析,结果如表4、表5所示,响应曲面如图6所示。
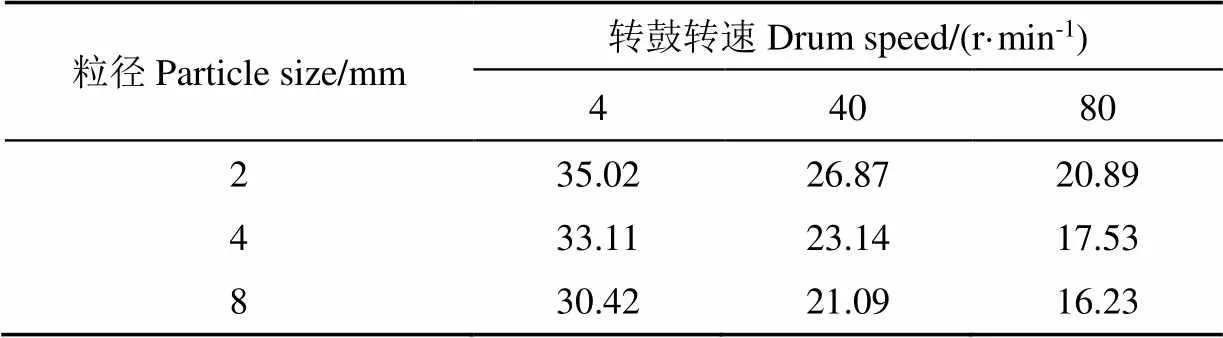
表2 动态堆积角试验结果
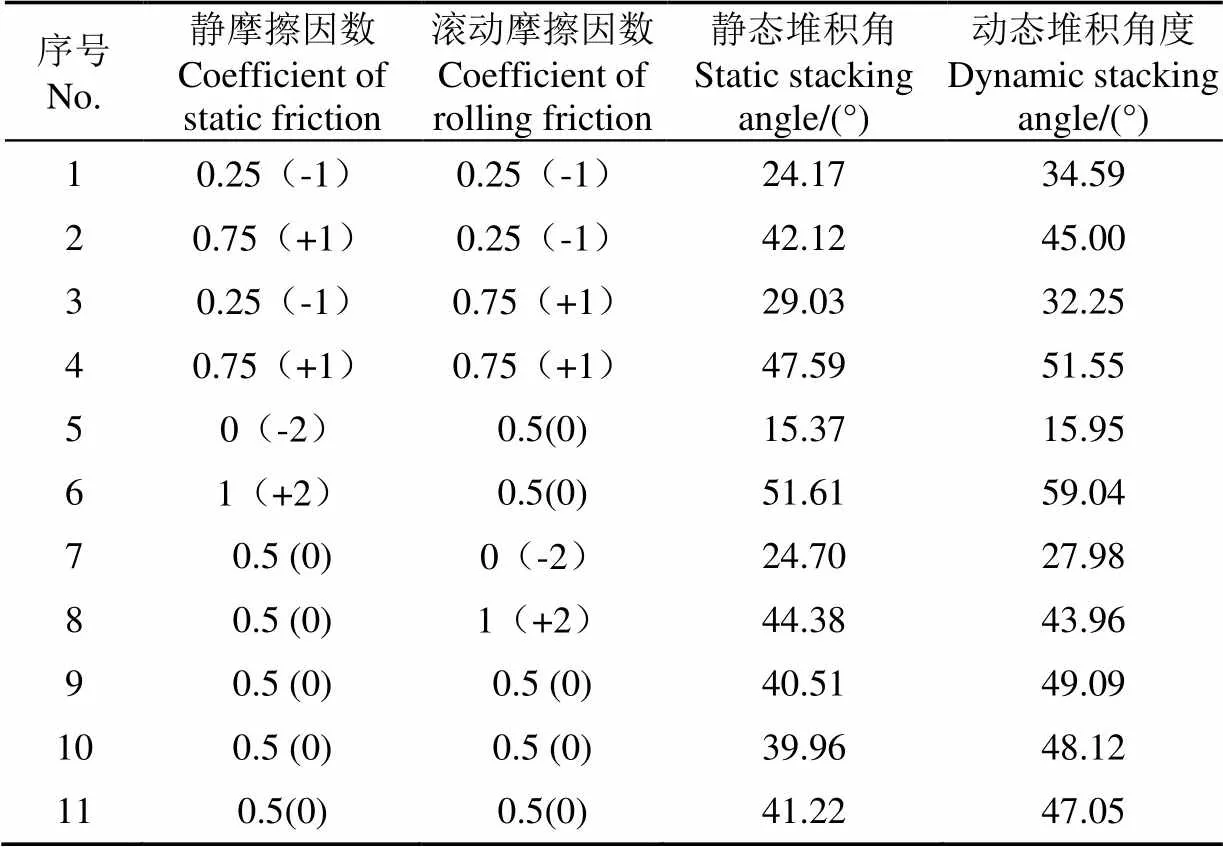
表3 仿真试验方案与结果
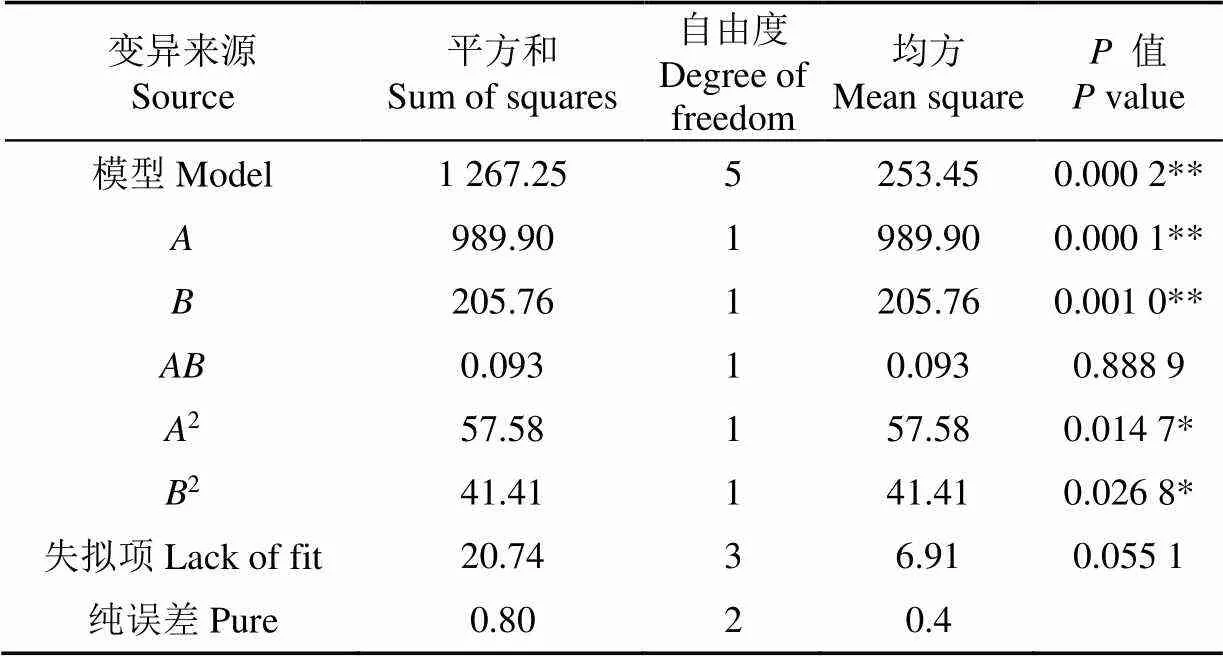
表4 静态堆积角R1模型方差分析
注:**极显著(<0.01),*显著(<0.05),下同。
Note: ** is highly significant (<0.01), * is significant (<0.05), the same below.
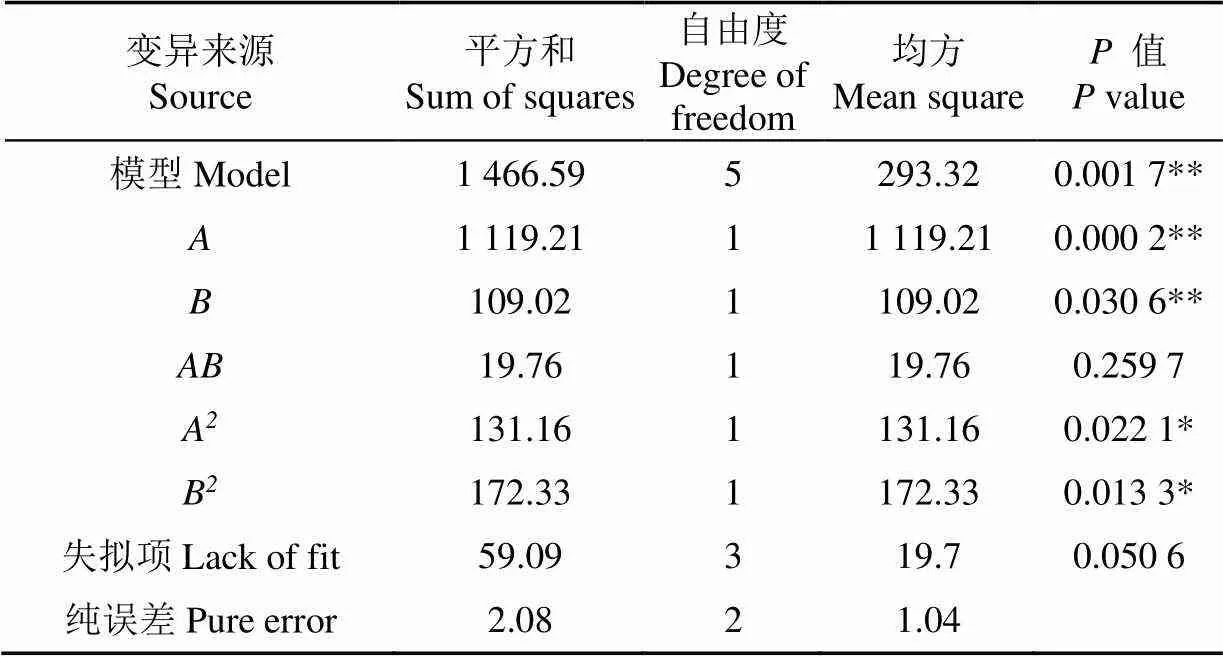
表5 动态堆积角R2模型方差分析
1模型显著性检验=0.000 2,决定系数2=0.98,失拟项=0.055 1,回归模型极显著,失拟项不显著,拟合程度较高。由表4可知,对土壤静态堆积角的影响,、极显著,2、2显著,影响显著从大到小顺序为、22试验因素与动态堆积角之间存在二次非线性关系,交互作用不显著,响应曲面如图6a所示,回归模型为:
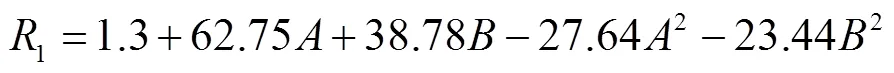
2模型显著性检验=0.001 7,决定系数2=0.96,失拟项=0.050 6,回归模型极显著,失拟项不显著,拟合程度较高。由表5可知,对土壤动态堆积角的影响,、极显著,2、2显著、影响显著顺序为>22试验因素与动态堆积角之间存在二次非线性关系,交互作用不显著,响应曲面如图6b所示,回归模型为:
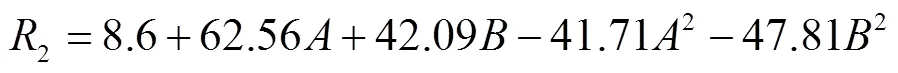

图6 双目标标定试验响应曲面
在Design-Expert V8.0.6.1软件中分别将静态堆积角与动态堆积角目标值设为32.16°、35.02°,进行双目标参数筛选,得到唯一解(=0.27,=0.70),双目标标定响应优化曲面如图7所示,唯一解在图中指出。依据所标定参数值,进行静态与动态堆积角仿真验证试验,其结果分别为32.43°、35.14°,误差分别为0.83%、0.34%,双目标标定结果较为可靠。仿真参数如表6所示[28-30]。
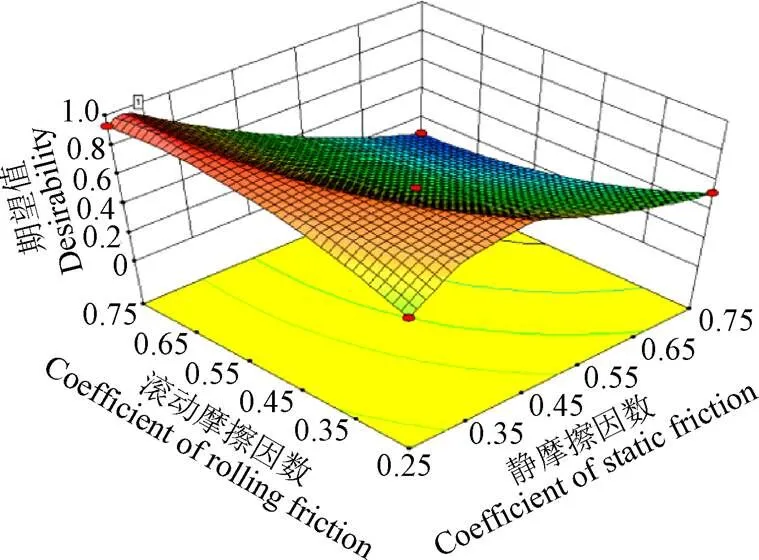
图7 双目标标定响应优化曲面
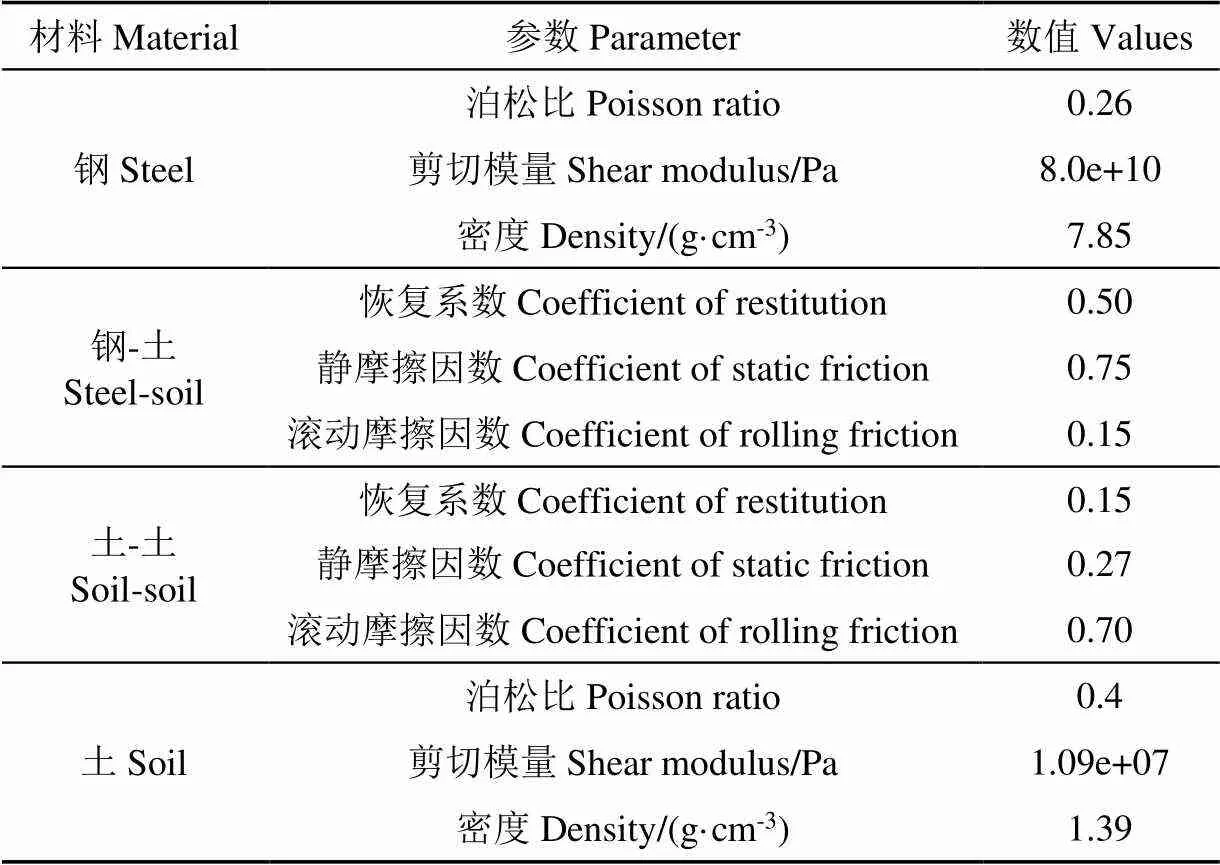
表6 仿真参数
在设定的3个转速下,对3组不同粒径沙壤土分别进行转鼓仿真对照试验[22],仿真试验过程如图8所示,得到动态堆积角结果如表7所示,两试验动态堆积角散点分布如图9所示。随后进行3种不同粒径下的坍塌与FT4流变仿真试验,并对不同颗粒群的流速、叶轮叶片所消耗能量进行数据分析。
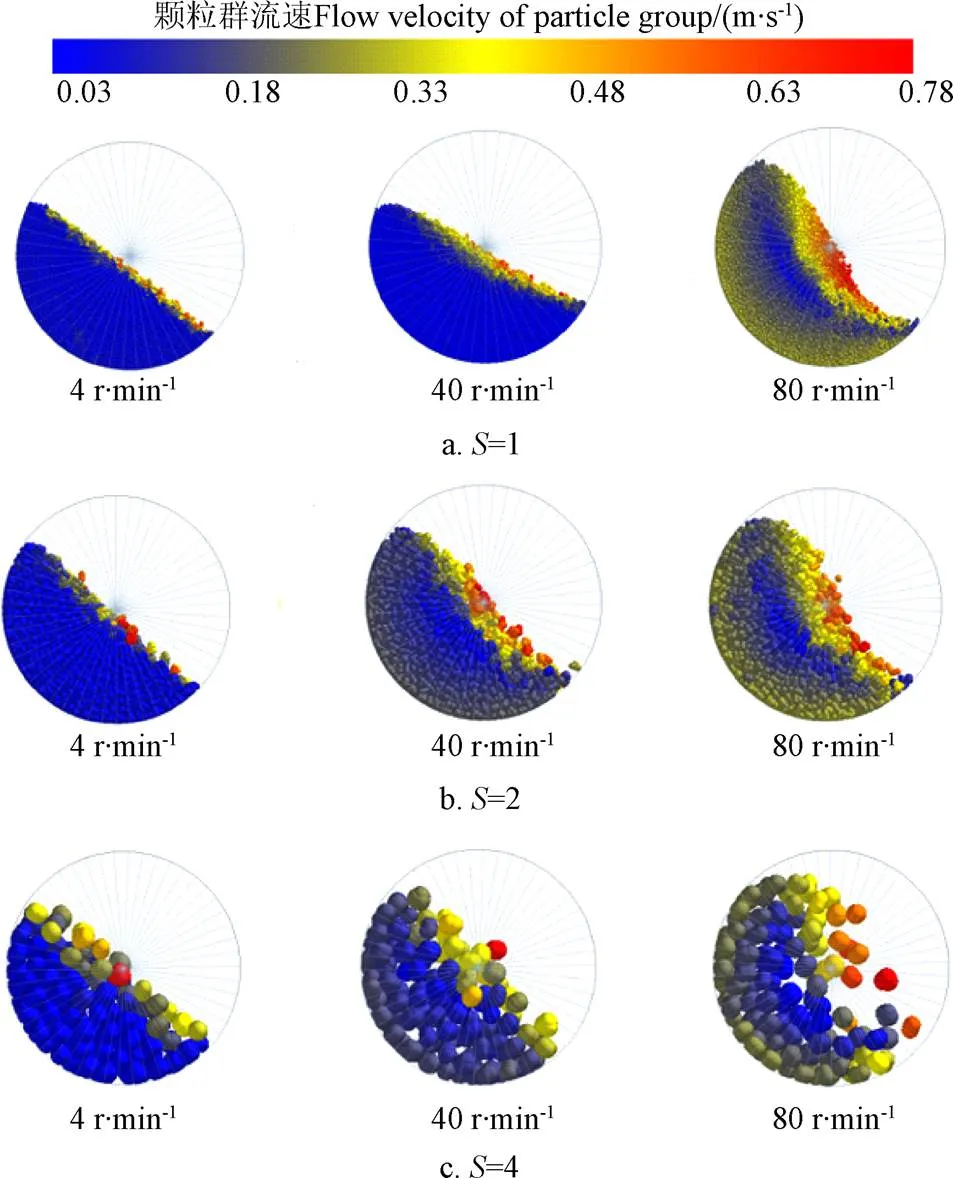
注:S为放尺因子,下同。

表7 动态堆积角仿真对照结果
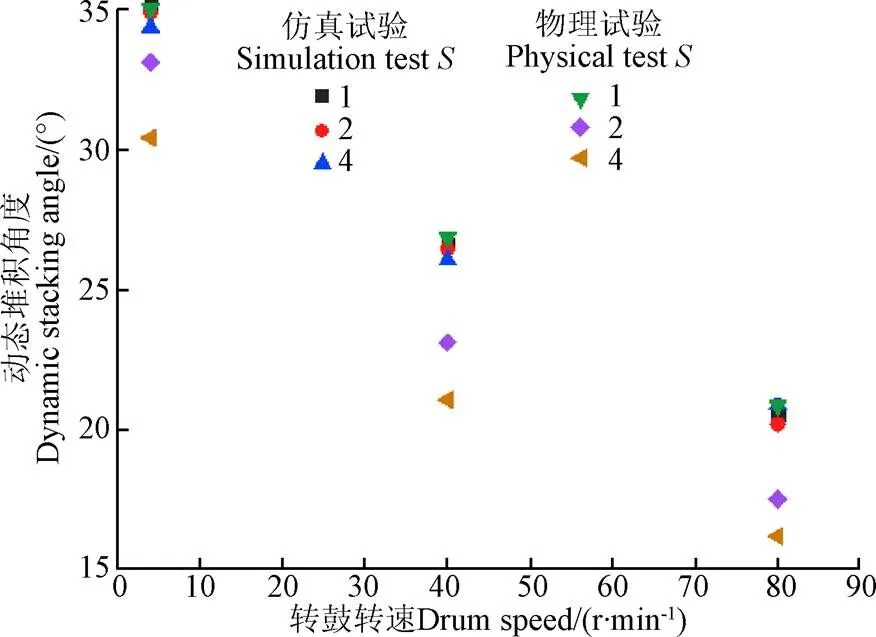
图9 动态堆积角度散点分布
2.2 试验结果分析
进行静态堆积角独立标定试验,得到沙壤土平均静态堆积角度为32.16°。从GEEM材料库中筛选出3组参数进行动态堆积角仿真试验,结果与实际试验存在较大差异,最小误差为5.51%。为提高仿真参数准确性,在转鼓为4 r/min的前提下,进行双目标标定试验,得到唯一解,依据所标定参数值,进行静态与动态堆积角仿真验证试验,结果分别为32.43°、35.14°,误差分别为0.83%、0.34%,表明2个独立标定试验较单个独立标定试验更容易获得唯一解且获得的参数更具代表性。随后,当转速提高至40、80 r/min后,该参数组合下得到的动态堆积角与实际试验结果依然较为接近,误差仅分别为0.78%和1.63%。表明进行两次独立标定试验较单一的标定试验标定结果更为可靠。但随着转鼓转速的增大,仿真与试验之间的误差逐渐增加。
实际转鼓试验现象:随着转鼓转速、粒径的增大,颗粒群在旋转过程中所表现出的离散程度不断增大,最终行成的堆积角度不断减小;仿真对照试验现象:随着转鼓旋转速度、粒径的增大,颗粒群形成的动态堆积角较为接近,且在流动过程中出现了明显的层流与抛洒现象,该现象与公式(2)的计算分析结果相吻合,表明了转鼓试验的科学性与可靠性。试验结果表明,放尺后动态堆积角与原尺基本保持一致(≤4时)。
坍塌仿真试验如图10所示。在软件中提取流量传感器中的质量与速度随时间变化数据进行对比分析。试验现象:不同粒径的颗粒群在流动过程中所体现出的流动质量与平均流速变化趋势基本一致,小粒径颗粒流速稍大于大粒径颗粒。从质量流量变化可以看出,颗粒群流量先是不断增大至一个极值点,随后流量趋于稳定,在小范围内出现上下波动,之后由于形成堆积角,质量开始上升,到达最高点处开始下降,直至固定在一个值,如图11a所示;从颗粒群平均流速可以看出,三者都经历了先增大,再降低直至速度为0,如图11b所示;从最终的堆积结果可以看出三者所形成的堆积角基本一致,但随着粒径的增大,误差有所增加。试验结果表明,随着粒径的不断增大,流量、速度差值也在随之增大。相比于流量,流速之间的差值较小,变化趋势相似程度较高。
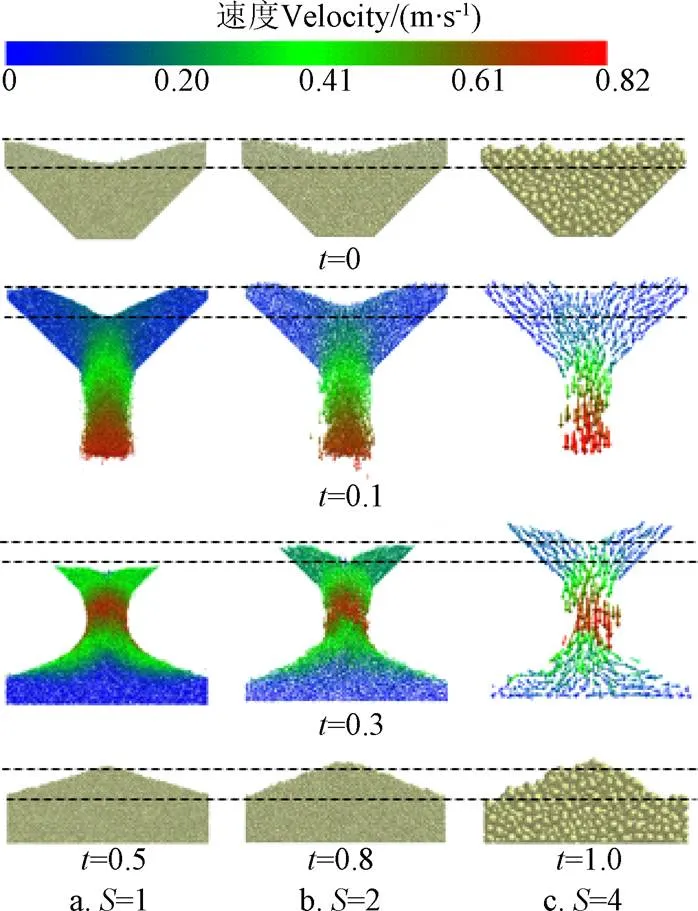
图10 坍塌仿真试验过程
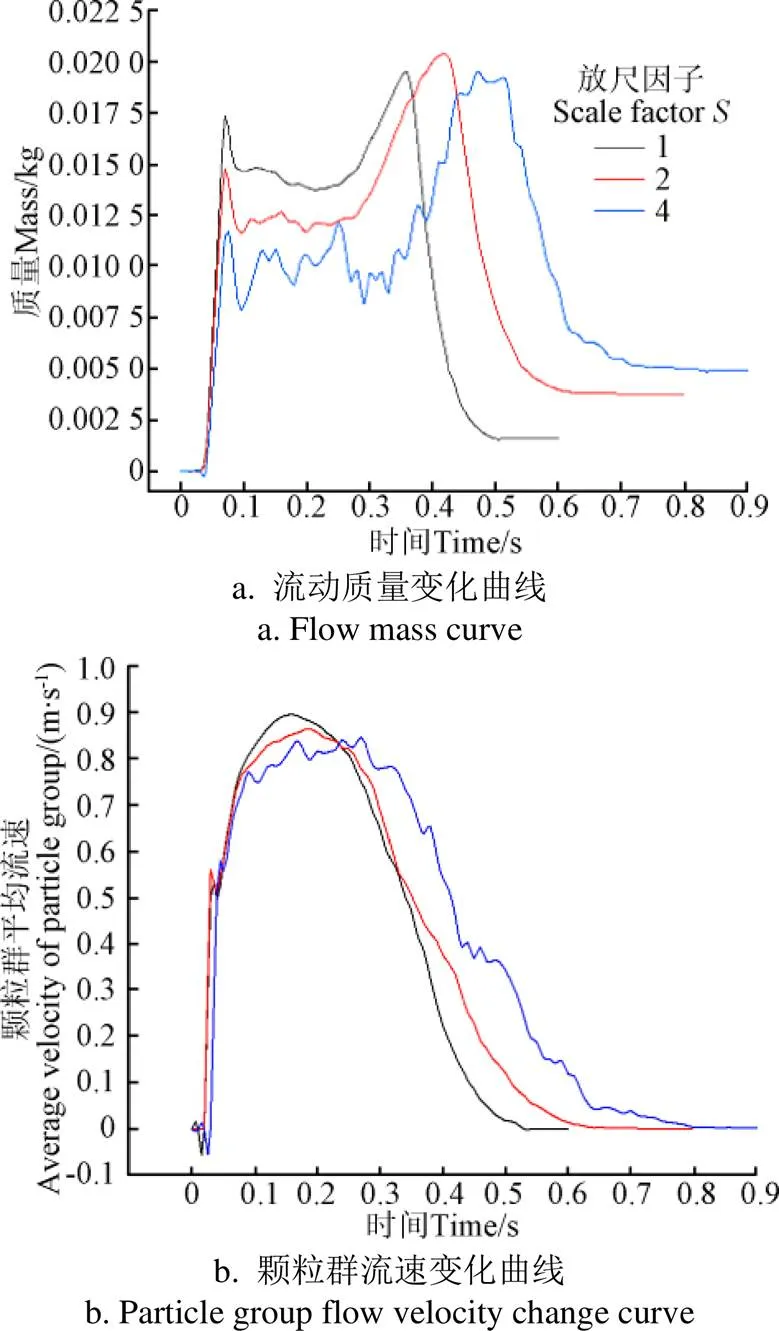
图11 坍塌试验质量与流速变化曲线
针对整个坍塌试验过程,本文使用同性能计算机将3组对比试验的瑞丽时间步长统一设定为20%、保存间隔为0.01 s、网格尺寸设定为3、保证相同的填充质量且未开启显卡加速模式(CPU为AMD 4800h),对仿真中总的颗粒数量及实际仿真所用时间平均值进行了数据分析,如图12所示。结果表明,随着颗粒尺寸的放大,总颗粒量与仿真时间大幅度下降。当=2时,颗粒量由原尺时的94 562减少至12 070,同比减少87.24%;当=4时,颗粒数量为1 018,同比减少了98.92%。所用仿真时间也大幅度下降,从=1到=4分别用时为7 665、905、181 s,分别减少了88.19%、97.64%,充分证明了进行颗粒放尺的优越性。
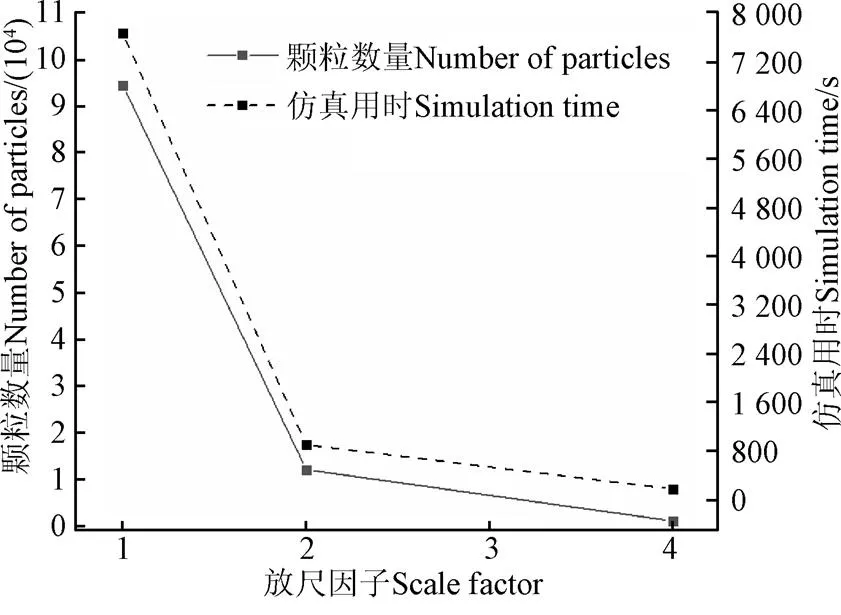
图12 仿真效率变化趋势
FT4流变仿真试验如图13所示。仿真试验过程中,叶轮叶片所受到的阻力及转矩如图14所示。
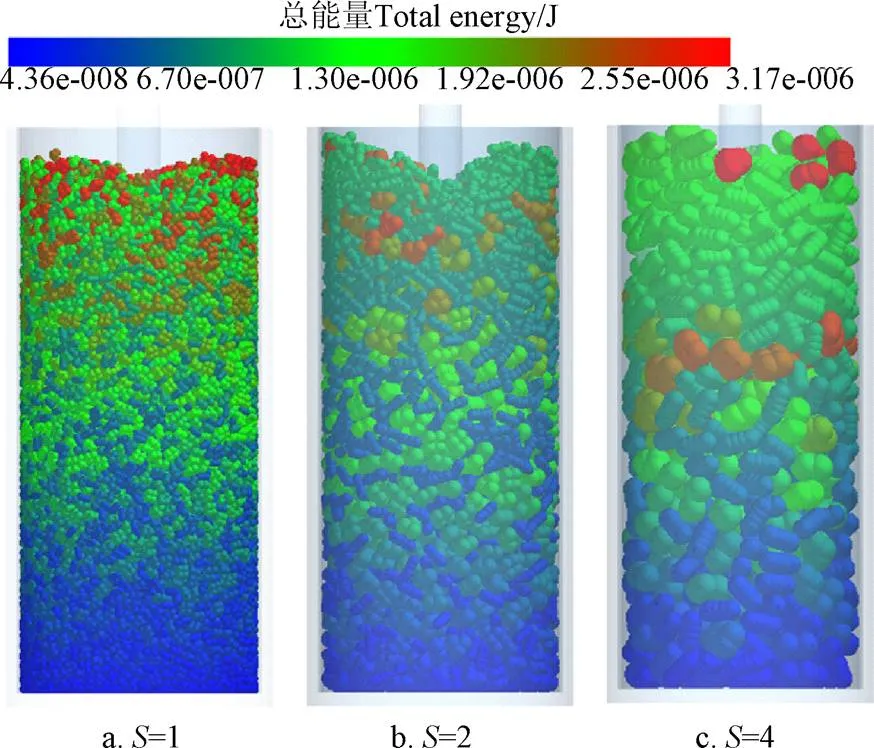
图13 FT4流变仿真试验
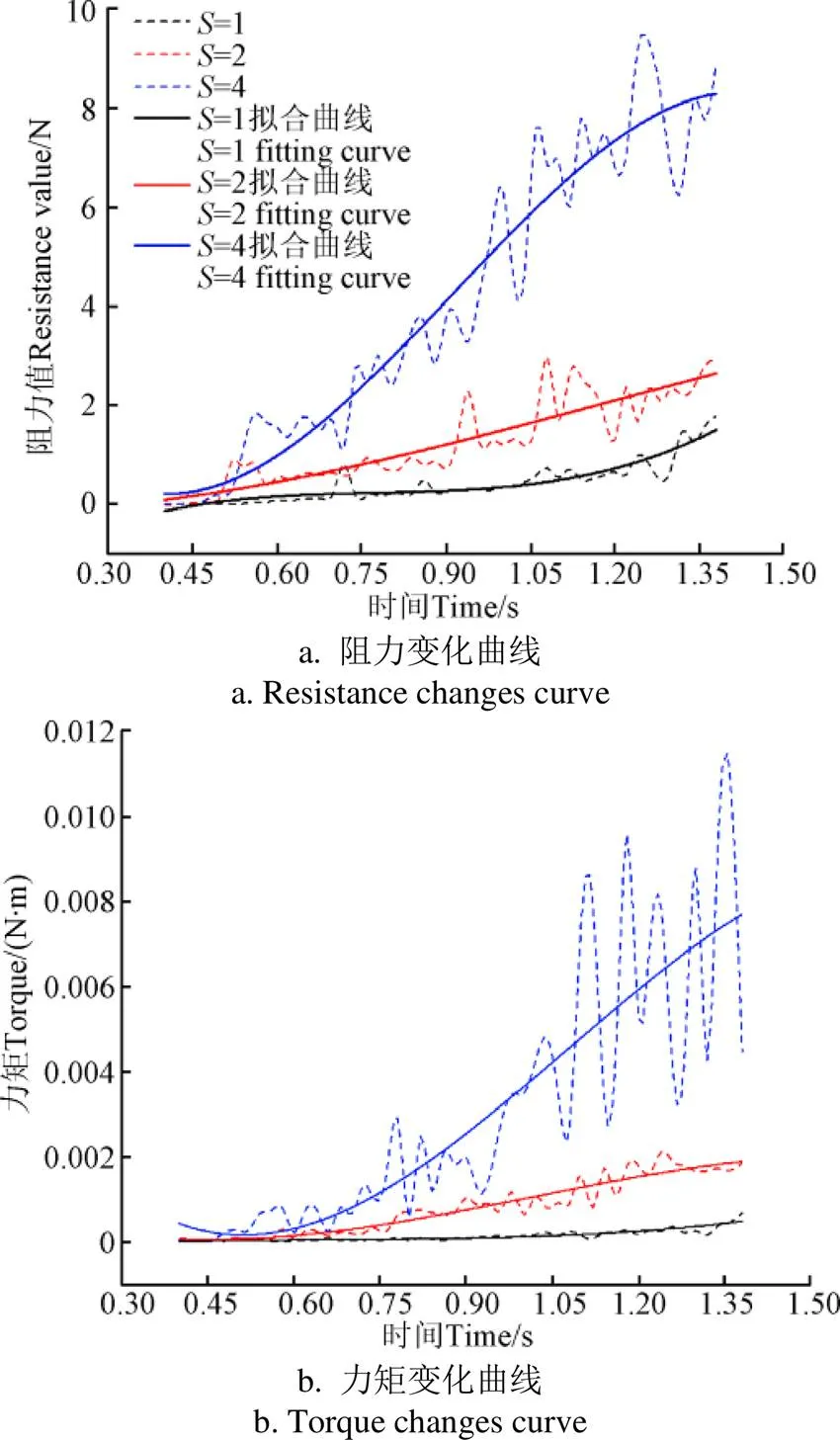
图14 力与力矩变化趋势
由图14可见,随着粒径的增大,阻力与转矩值增大,曲线波动范围越来越大,即误差增大。但图13a、b中当放尺因子为1和2时得到的2条3次方拟合曲线从1 s后曲率趋于平缓,斜率较为接近,同一时刻,两曲线上点的差值约为2倍,具有良好的线性关系,可近似认为放尺2倍后,叶片受到的阻力及转矩约为未放尺时的2倍,由公式(3)可知,叶片所消耗功耗也约为未放尺时的2倍;而放尺因子分别为1和4时得到的2条拟合曲线斜率差异显著。
3 结 论
本文以沙壤土作为研究对象,在离散元软件中构建非球形颗粒,进行双目标参数标定试验并采用放大单个颗粒尺度的方法,通过转鼓、坍塌与FT4流变仿真试验,从动态堆积角度、颗粒群流量、流速、阻力、转矩以及能量等方面探究了颗粒放尺效应对颗粒群物理特性的影响,得到如下结论:
1)进行2个独立标定试验得到的仿真参数相较于单个独立标定实验值更具唯一性及代表性。
2)在动态堆积角试验中,真实沙壤土颗粒在转鼓中所形成的动态堆积角随粒径和旋转速度的增大而不断减小;在仿真试验中,非球形颗粒群在放尺后所形成的动态休止角与原尺基本保持一致,但误差随放尺因子的增大而增大。
3)在坍塌试验中,不同粒径颗粒群在流动过程中所体现出的流动质量与平均流速变化趋势基本一致,随着粒径的不断增大,流量、流速误差随之增大。相同计算域中的颗粒量同比分别减少了87.24%(放尺因子为2时)、98.92%(放尺因子为4时),所用仿真时间明显降低,分别减少了88.19%、97.64%,尤其当放尺因子为2时,计算效率相较于原尺颗粒显著提高。
4)在FT4流变试验中,得到了颗粒放尺后叶轮叶片所受到的阻力与力矩相较于原尺两者之间的关系:可近似认为放尺2倍后,叶片受到的阻力、转矩以及叶片所消耗的功耗约为未放尺时的2倍。
5)通过仿真参数标定,适当放大颗粒尺寸进而减小计算量的方法是可行的,计算效率也会得到很大提高,但是随着放尺因子的不断增大,误差也在不断加大,因此放尺因子取决于仿真工况,针对不同的仿真工况而言,要充分考虑到放尺因子、仿真误差以及仿真效率三者之间的关系,将误差控制在可允许范围内。本研究中当=2时,仿真过程中沙壤土的流动效应与原尺基本一致,针对本文麻山药-沙壤土复合体离散元收获仿真工况,放尺因子拟定为2,后续拟将收获仿真中机具所受阻力值缩小两倍并与田间试验结果进行比对,进一步验证颗粒放尺的准确性。
[1] 郝建军,龙思放,李浩,等. 机收麻山药离散元模型构建及其仿真参数标定[J]. 农业工程学报,2019,35(20):34-42.
Hao Jianjun, Long Sifang, Li Hao, et al. Development of discrete element model and calibration of simulation parameters for mechanically-harvested yam[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(20): 34-42. (in Chinese with English abstract)
[2] 马跃进,王安,赵建国,等. 基于离散元法的凸圆刃式深松铲减阻效果仿真分析与试验[J]. 农业工程学报,2019,35(3):16-23.
Ma Yuejin, Wang An, Zhao Jianguo, et al. Simulation analysis and experiment of drag reduction effect of convex blade subsoiler based on discrete element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(3): 16-23. (in Chinese with English abstract)
[3] 张锋伟,宋学锋,张雪坤,等. 玉米秸秆揉丝破碎过程力学特性仿真与试验[J]. 农业工程学报,2019,35(9):58-65.
Zhang Fengwei, Song Xuefeng, Zhang Xuekun, et al. Simulation and experiment on mechanical characteristics of kneading and crushing process of corn straw[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(9): 58-65. (in Chinese with English abstract)
[4] 刘文政,何进,李洪文,等. 基于离散元的微型马铃薯仿真参数标定[J]. 农业机械学报,2018,49(5):132-142,149.
Liu Wenzheng, He Jin, Li Hongwen, et al. Calibration of simulation parameters for potato minituber based on EDEM[J].Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(5): 132-142, 149. (in Chinese with English abstract)
[5] 王安,马跃进,赵建国,等. 凸圆滑切式减阻深松铲尖设计与试验[J]. 河北农业大学学报,2019,42(3):109-114.
Wang An, Ma Yuejin, Zhao Jianguo, et al. Design and experiment of convex and sliding anti-drag deep-shovel tip[J]. Journal of Hebei Agricultural University, 2019, 42(3): 109-114. (in Chinese with English abstract)
[6] Stef Lommen, Mohammadjavad Mohajeri, Gabriel Lodewijks, et al. DEM particle upscaling for large-scale bulk handling equipment and material interaction[J]. Powder Technology, 2019, 352: 273-282
[7] 邓益兵,杨彦骋,史旦达,等. 三维离散元大尺度模拟中变粒径方法的优化及其应用[J]. 岩土工程学报,2017,39(1):62-70.
Deng Yibing, Yang Yancheng, Shi Danda, et al. Refinement and application of variable particle-size methods in 3D discrete element modelling for large-scale problems[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(1): 62-70. (in Chinese with English abstract)
[8] Schott D L, Lommen S W, Van Gils R, et al. Scaling of particles and equipment by experiments of an excavation motion[J]. Powder Technology, 2015, 278: 26-34.
[9] Subhash C, Thakur, Jin Y, et al. Scaling of discrete element model parameters for cohesionless and cohesive solid[J]. Powder Technology, 2016, 293:130-137
[10] Windows-Yule C R K, Tunuguntla D R, Parker D J. Numerical modelling of granular flows: A reality check[J]. Computational Particle Mechanics, 2015, 3(3): 311-332.
[11] Thomas Roessler, André Katterfeld. Scaling of the angle of repose test and its influence on the calibration of DEM parameters using upscaled particles[J]. Powder Technology, 2018, 330: 58-66.
[12] Munjiza A, Feng Y T, Loughran J. On upscaling of discrete element models: Similarity principles[J]. Engineering Computations, 2009, 26(6): 599-609.
[13] William Smith, Daniel Melanz, Carmine Senatore, et al. Comparison of discrete element method and traditional modeling methods for steady-state wheel-terrain interaction of small vehicles[J]. Journal of Terramechanics, 2014, 56: 61-75.
[14] Matteo Oryem Ciantia, Marcos Arroyo, Joanna Butlanska, et al. DEM modelling of cone penetration tests in a double-porosity crushable granular material[J]. Computers and Geotechnics, 2016, 73: 109-127.
[15] Matthew D, Sinnott, Paul W, et al. The effect of particle shape on mixing in a high shear mixer[J]. Computational Particle Mechanics, 2016, 3(4): 477-504.
[16] Wang Z, Jacobs F, Ziegler M. Experimental and DEM investigation of geogrid-soil interaction under pullout loads[J]. Geotextiles and Geomembranes, 2016, 44(3): 230-246.
[17] Grima A P, Wypych P W. On improving the calibration and validation of computer simulations for bulk materials handling systems[A]. Australian Bulk Handling Review, 2009: 84-91.
[18] Xie Liyu, Zhong Wenqi, Zhang Hao, et al. Wear process during granular flowtransportation in conveyor transfer[J]. Powder Technology, 2016, 288: 65-75.
[19] Grima A P, Wypych P W. Investigation into calibration of discrete element model parameters for scale-up and validation of particle-structure interactions under impact conditions[J]. Powder Technology, 2011, 212(1): 198-209.
[20] 李毓,李林安,陈坤生,等. 基于离散单元法的粗粒料缩尺效应探究[J]. 铁道科学与工程学报,2018(7):1722-1729.
Li Yu, Li Lin’an, Cheng Kunsheng, et al. Study on the relationship between particle size distribution and stress-strain of soil[J]. Journal of Railway Science and Engineering, 2018(7): 1722-1729. (in Chinese with English abstract)
[21] Coetzee C J. Particle upscaling: Calibration and validation of the discrete element method[J]. Powder Technology, 2019, 344: 487-503.
[22] Tiscar J M, Escrig A, Mallol G, et al. DEM-based modelling framework for spray-dried powders in ceramic tiles industry. Part I: Calibration procedure[J]. Powder Technology, 2019, 356: 818-831.
[23] Rößler T, Richter C, Katterfeld A, et al. Development of a standardcalibration procedure for the DEM parameters of cohesionless bulk materials.Part I - Solving the problem of ambiguous parameter combinations[J]. Powder Technology, 2019, 343: 803-812.
[24] 夏鹏,李郁,杨公波. 散粒物料堆积角离散元仿真研究[J].起重运输机械,2015(2):107-110.
Xia Peng, Li Yu, Yang Gongbo. Study on the discrete element simulation of scattered materials[J]. Hoisting and Conveying Machinery, 2015(2): 107-110. (in Chinese with English abstract)
[25] 韩燕龙,贾富国,唐玉荣,等. 颗粒滚动摩擦系数对堆积特性的影响[J]. 物理学报,2014,63(17):4501-4507.
Han Yanlong, Jia Fuguo, Tang Yurong, et al. Influence of granular coefficient of rolling friction on accumulation characteristics[J]. Acta Physica Sinica, 2014, 63(17): 4501-4507. (in Chinese with English abstract)
[26] Mellmann J. The transverse motion of solids in rotating cylinders-forms of motionand transition behavior[J]. Powder Technol, 2001, 18(3): 251-270.
[27] Freeman R. Measuring the flow properties of consolidated, conditioned and aerated powders: A comparative study using a powder rheometer and a rotational shear cell[J]. Powder Technology, 2007, 174(1/2): 25-33.
[28] 张锐,韩佃雷,吉巧丽,等. 离散元模拟中沙土参数标定方法研究[J]. 农业机械学报,2017,48(3):49-56.
Zhang Rui, Han Dianlei, Ji Qiaoli, et al. Calibration methodsof sandy soil parameters in simulation of discrete element method[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(3): 49-56. (in Chinese with English abstract)
[29] 毕秋实,王国强,陈立军,等. 基于离散元-多体动力学联合仿真的机械式挖掘机挖掘阻力仿真与试验[J]. 吉林大学学报:工学版,2019,49(1):106-116.
Bi Qiushi, Wang Guoqiang, Chen Lijun, et al. Numerical simulation and experiment on excavation resistance of mechanical excavator based on DEM-MBD co-simulation[J]. Journal of Jilin University: Engineering and Technology Edition, 2019, 49(1): 106-116. (in Chinese with English abstract)
[30] 程一启,张兆国,张丹,等. 三七收获机组合式挖掘铲减阻效果研究:基于EDEM[J]. 农机化研究,2019,41(2):55-60.
Cheng Yiqi, Zhang Zhaoguo, Zhang Dan, et al. Research of resistance reduction effect of panax notoginseng harvest combined digging shovel: Based on EDEM[J]. Journal of Agricultural Mechanization Research, 2019, 41(2): 55-60. (in Chinese with English abstract)
Effect of granular ruler in discrete element model of sandy loam fluidity in Ma yam planting field
Hao Jianjun, Long Sifang, Li Jianchang, Ma Zhikai, Zhao Xiaoshun, Zhao Jianguo, Li Hao
(,,071000,)
This study aims to significantly improve the computational efficiency of discrete element method (DEM) in the agricultural field, particularly in the simplified model for harvesting the yam-sandy loam soil complex. Taking the sandy loam soil as the research object, the dual-target parameter calibration experiments were used to construct non-spherical particles in the discrete element software, together with enlarging the size of a single particle. The dynamic accumulation angle, flow quality, and flow rate were determined in the drum and collapse tests, and thereby to explore the influence of particle ruler effect on the flow characteristics in the particle group. The maximum scale factor of particles in the model was set as=4, and the rotating speed of drum was set as4rpm, 40rpm, and 80rpm, respectively. The dynamic angles of repose in the particle group were measured in the actual and simulation test. Subsequently, a collapse test was carried out to monitor the discharge outlet flow during the collapse of particle groups’ indifferent sizes. The test results show that the average static accumulation angle of 2mm sandy loam matrix after drying treatment was 32.16°, and the average dynamic accumulation angle was 35.02°. The simulation parameters obtained from the dual-target calibration test were more accurate than that from the independent calibration test. The dynamic accumulation angle that formed by the real sandy loam particles in the drum decreased with the increase of particle size and rotation speed, while, the non-spherical particle group only changed the particle size in the simulation test. There was a relatively small difference in the dynamic angle of repose that produced in the case of diameter. In the collapse test, the changing trend of flow quality representing by the particle groups of different diameters in the flow process was basically the same as that of average flow velocity. The error was also increasing with the continuous increase of diameter. The amount of particles in the same calculation domain decreased by 87.24% (=2) and 98.92% (=4), respectively, indicating that the simulation time significantly reduced. Especially, when=2, the calculation efficiency was significantly improved, compared with that of the non-stretched particles. The FT4 rheological test showed that when the scaling factorwas 2, the fitting curve of resistanceFand its torquewith the time changes was about twice that of the unfolding factor. When the scaling factorwas 4, the slopes of two fitted curves were totally different, indicating that the correlation was significantly reduced, compared with the original ruler. The findings can provide a sound theoretical basis on the construction of discrete element scaling model for the sandy loam soil, and the simulation calculation in agricultural engineering.
soils; models; particle scale; sandy loam flow characteristics; calibration test
郝建军,龙思放,李建昌,等. 麻山药种植田沙壤土流动性离散元模型颗粒放尺效应[J]. 农业工程学报,2020,36(21):56-64.doi:10.11975/j.issn.1002-6819.2020.21.007 http://www.tcsae.org
Hao Jianjun, Long Sifang, Li Jianchang, et al. Effect of granular ruler in discrete element model of sandy loam fluidity in Ma yam planting field[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(21): 56-64. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2020.21.007 http://www.tcsae.org
2020-08-07
2020-09-25
河北省农机新机具新技术研发项目(2020)
郝建军,教授,博士生导师,主要从事农业生产自动化技术及装备研究。Email:hjjpaper@163.com
10.11975/j.issn.1002-6819.2020.21.007
S539:S313
A
1002-6819(2020)-21-0056-09
