别让数学学习策略无用武之地

陈算荣 张波

摘要：测评分析发现，数学高考成绩显著好的学校的学生，在数学学习策略各个维度的掌握和使用水平上，基本都没有高于——甚至在很多维度上低于数学高考成绩显著差的学校的学生。究其原因，教师的大量灌输和题海战术，使学生没有时间和空间在学习活动中充分体会和运用学习策略。对此，需要反思和警醒：采取有效的教学策略，并把学习的时间和空间适当还给学生，帮助学生充分掌握、合理使用学习策略，才是“发展学生核心素养”的“轻负高效”教学的应有之义。

关键词：数学学习策略;测评分析;核心素养;“轻负高效”

一、问题提出

“学会学习”是中国学生需要发展的六大核心素养之一。学习策略是“学会学习”的一种具体表现。因此，可以通过测评学生的学习策略，对学生的“学会学习”素养洞察一二。

学习策略是一个包含很广、很难概括、目前还没有统一界定的概念。一切有助于学习的外显或内隐的程序、方法及规则都属于学习策略。一些实证研究表明，某些学习策略的有效运用和学生的某些学习成绩有较高的正相关性。例如，有研究结果表明，学生在精加工策略使用上的得分和他们阅读测验的分数有高度相关性。在数学教育方面，国内外的许多实证研究同样表明，合理有效的、运用良好的数学学习策略能帮助学生提高数学成绩。但是，也有实证研究发现，随着年级的增高、课业负担的增重，学习策略对学业成绩的影响效力变得很小。

当前，在课程改革不断深化的背景下，我们注意到，一些学校逆“发展学生核心素养”的“轻负高效”（少而精）教学之道而行，变本加厉地“刷题”应试，导致学生的课业负担不断加重。在这种教育生态下，学生数学学习策略的掌握和使用情况如何，数学学习策略对数学学业成绩的影响如何，是值得研究的问题。

二、研究方法

我们选取某一线城市某区一所“最好”的市级重点高级中学（A校）和该区一所“最差”的普通公立高级中学（B校）的高三学生作为研究对象。两所学校当年数学高考的均分相差30多分。

运用王光明教授等人在《高中生数学学习策略调查问卷的编制》一文中给出的高中生数学学习策略調查问卷，测评研究对象学习策略的掌握和使用情况。这一问卷将数学学习策略分为3个主维度（认知策略、元认知策略、资源管理策略），并进一步分为11个子维度（复述策略、精加工策略、组织策略、反馈策略，计划策略、监视策略、反思调节策略，时间管理策略、环境管理策略、心境管理策略、外界求助策略），对每个子维度分别设计若干测试题，共设计51题（2题用于信度检测，另外49题用于实际测评）。计分方式采用的是李克特五点评分法：从“非常符合”“符合”“基本符合”“不符合”到“非常不符合”依次计分为5、4、3、2、1。

发放问卷260份。剔除无效问卷（含有未答选项或测谎题的相关性低）后，收回有效问卷243份，其中A校130份，B校113份。用G.Power软件进行样本容量检测，在给定效应值为0.5，错误概率（error probability）值为0.05，统计功效（power）值为0.95的条件下，分析得到样本容量在176以上为合适。所以，243这样的样本容量符合本研究的要求。此外，本次测评的信度（Cronbach）值为0.79（大于0.7），信度良好。

三、结果分析

我们主要运用SPSS 21.0软件对测评结果进行独立样本均值和方差比较分析，从主维度和子维度两个层面分析两所学校学生学习策略掌握和使用情况的差异。

（一）3个主维度的比较分析

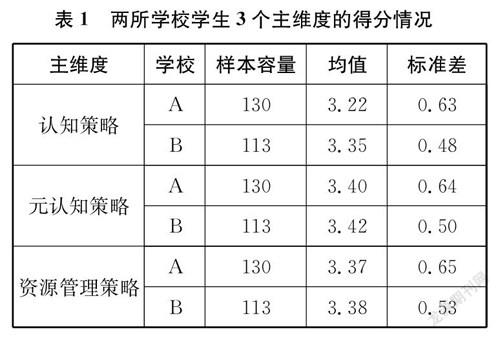
数据分析结果（见表1）显示：两所学校学生3个主维度的得分均值都在3—3.5之间。这说明两所学校学生的认知策略、元认知策略、资源管理策略掌握和使用水平都不是很高，处于中等水平。另外，3个主维度的得分均值都是“差”学校的学生略高于“好”学校的学生。这说明学生的学习策略掌握和使用水平与学习成绩并不是正相关的，甚至呈现一种倒挂现象。

独立样本检验结果表明：在假设方差不相等的情况下（F=4.32，p=0.04<0.05），两所学校学生的认知策略掌握和使用水平没有统计学上的显著差异（t=-1.81，df= 237，p=0.07>0.05）;在假设方差相等的情况下（F=2.753，p=0.10>005），两所学校学生的元认知策略掌握和使用水平没有统计学上的显著差异（t=-0.17，df=241，p=0.86>0.05）;在假设方差相等的情况下（F=2.61，p=0.11>0.05），两所学校学生的资源管理策略掌握和使用水平也没有统计学上的显著差异（t=-1.43，df=241，p= 0.89>0.05）。

（二）11个子维度的比较分析

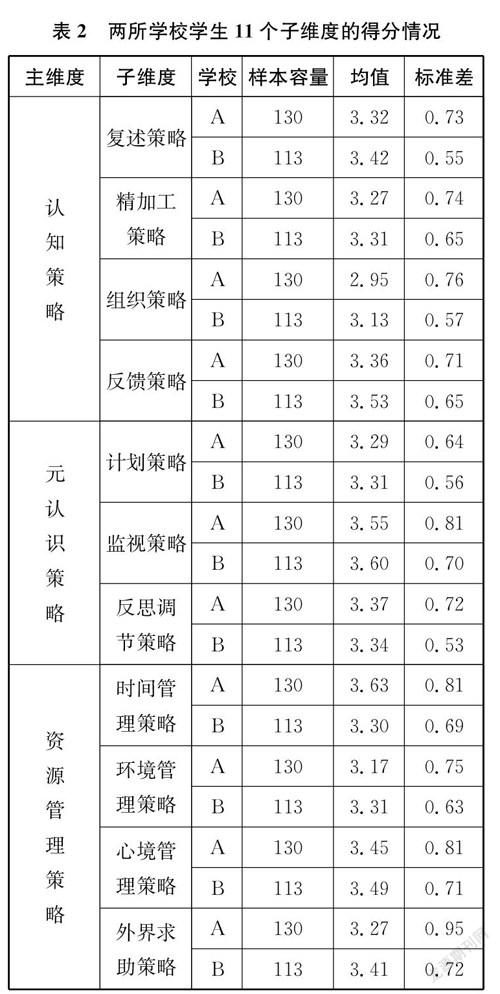
数据分析结果（见下页表2）显示：除了反思调节策略和时间管理策略的掌握和使用水平是“好”学校的学生略高于“差”学校的学生之外，其余9个学习策略的掌握和使用水平都是“差”学校的学生略高于“好”学校的学生。

独立样本检验结果表明：在假设方差不相等的情况下（F=6.88，p=0.01<0.05），两所学校学生的组织策略掌握和使用水平存在统计学上的显著差异（t=-2.12，df= 237，p=0.04<0.05）;在假设方差相等的情况下（F=0.29，p=0.59>005），两所学校学生的反馈策略掌握和使用水平存在统计学上的显著差异（t=-1.94，df=241，p=0.05）;在假设方差不相等的情况下（F=3.90，p=0.05），两所学校学生的时间管理策略掌握和使用水平存在统计学上的显著差异（t=3.46，df=241，p<0.01）;而两所学校学生的其他8个学习策略掌握和使用水平都不存在统计学上的显著差异。

可见，“好”学校的学生更懂得运用时间管理策略，而“差”学校的学生更善于运用组织策略和反馈策略。

四、结论探讨

上述结果分析表明，数学高考成绩显著好的学校的学生，在数学学习策略各个维度的掌握和使用水平上，基本都没有高于——甚至在很多维度上低于数学高考成绩显著差的学校的学生。这一结论与已有的很多实证研究结论不吻合。其背后的原因是什么？反映了怎样的教育现实问题？

在上述数据分析的基础上，我们采用非结构化访谈方法，随机采访了“好”学校和“差”学校学生的学习情况。访谈发现，“好”学校的学生从高一开始，就要做很多超出高一知识范畴的综合性难题，很多题目来自高三的模拟考试卷。可以想象，从高一到高三，“好”学校的学生要多花出多少时间和精力用在“遨游题海”及解答难题上。此外，他们课余多奔走于各种补习班之间，继续疯狂“刷题”，因而几乎没有自主使用学习策略的时间和空间。相反，“差”学校的学生在做题的数量和难度上都远远不及“好”学校的学生，因此反而拥有较多的时间和空间自主使用学习策略。但是，他们入学时的学习起点低，平时训练的强度也低，这使得他们的高考成绩与“好”学校的学生差距依然很大。当然，不排除这样一种可能：高考成绩的差距与当年高中入学时中考成绩的差距相当或者已缩小。对此，需要展开一项新的研究进行追踪分析。

当然，还可能有其他因素造成两所学校学生数学成绩的差距，如学习资源、家庭支持等。但是，学习策略和学习成绩成正相关这个关系的弱化或倒挂反映了当前学生的学习情况：基本处于教师的大量灌输和题海战术中，没有时间和空间在学习活动中充分体会和运用学习策略，只能机械地、被动地、疲惫地完成教师布置的超负荷任务。

另一个深层次原因则是课堂教学问题。在某省一个为期5天的高中骨干教师培训课程中，参与者以“发展学生逻辑推理素养”为专题开展了一次观课和研课活动，课题为“求函数的解析式”。我们就日常教学中大家如何上这节课做了调研，得到几乎一致的回应是：习题课的教学主要是训练学生解题归类;这节课的教学主要是告诉学生哪种题型可用待定系数法，哪种题型可用换元法，哪种题型可用定值代入法等。而对通过解决问题帮助学生理解函数的本质，激发学生深层次的思考和推理分析的教学策略则较少提及。可见，粗暴式的“讲题、练题、套题”教学已经根植于很多教师的教学行为中。

五、研究启示

实际上，适当“刷题”和解题归类固然是需要的，但是，在问题解决的过程中回归数学知识本质分析和领会数学思想方法运用才是關键。这样的教学才能让学生真正做到举一反三，有效迁移旧知识到新情境中解决新问题。习题课的教学如是，概念课、定理课、公式课等的教学亦如是。教师应该采取有效的教学策略，并把学习的时间和空间适当还给学生，帮助学生充分掌握、合理使用学习策略。这是“发展学生核心素养”的“轻负高效”教学的应有之义。

上述数学学习策略掌握和使用情况的测评分析结论在“意料之外”，但是，洞悉当前的教学现状后，发现其又在“情理之中”。当然，这一结论只是基于对两所非典型学校的个案式研究得到的。学习策略无用武之地究竟是个别现象还是普遍现象，还需要在更大的样本空间中探查。但是，反思和警醒是必要的。

参考文献：

[1] 史耀芳.二十世纪国内外学习策略研究概述[J].心理科学，2001（5）.

[2] 张晖，单肖天.初中数学学习策略的构建及教学[J].课程·教材·教法，1997（10）.

[3] 叶艳丽，喻平.学习策略的心理学研究及其对小学数学教学的启示[J].教育研究与评论（小学教育教学），2021（2）.

[4] 刘旭晨，喻平.学习策略的心理学研究及其对中学数学教学的启示[J].教育研究与评论（中学教育教学），2021（4）.

[5] 张庆林.当代认知心理学在教学中的应用[M].重庆：西南师范大学出版社，1995.

[6] 莫秀锋，刘电芝.初中生数学学习策略的可控心理影响机制[J].心理与行为研究，2005（4）.

[7] 李毅侠.高中生数学学习策略调查研究[J].教学与管理，2001（15）.

[8] 谷生华，辛涛，李荟.初中生学习归因、学习策略与学习成绩关系的研究[J].心理发展与教育，1998（2）.

[9] 刘志华，郭占基.初中生的学业成就动机、学习策略与学业成绩关系研究[J].心理科学，1993（4）.

[10] 徐速，朱燕.初中数学学习中教师归因与学生自我归因的比较研究[J].心理科学，2001（1）.

[11] M.Hegarty，R.E.Mayer，C.A.Monk. Comprehension of arithmetic word problem： A comparison of successful and unsuccessful problem solvers[J].Journal of Educational Psychology，1995（1）.

[12] R.S.Bander， R.K.Russell，K.P.Zamostny，et al. A comparison of cuecontrolled relaxation and study skills counseling in the treatment of mathematics anxiety[J].Journal of Educational Psychology，1982（1）.

[13] Kenichi Machida，Jerry Carlson.Effects of a verbal mediation strategy on cognitive processes in mathematics learning [J]. Journal of Educational Psychology，1984（6）.

[14] P.Pokay，P.C.Blumenfeld.Predicting achievement early and late in the semester： The role of motivation and use of learning strategies[J]. Journal of Educational Psychology，1990（1）.

[15] 刘电芝，朱江容，丁小强，等.策略意识对初中生数学学习策略的影响：策略情感的中介效应[J].苏州大学学报（教育科学版），2015（1）.

[16] 王光明，廖晶，黄倩，等. 高中生数学学习策略调查问卷的编制[J].数学教育学报，2015（5）.