文科类院校“数值计算”课程开展实践

邓小毛 廖子菊

摘要“数值计算”是一门研究用计算机程序解决数学物理问题的方法及其理论的课程，是计算数学方向重要的基础入门课。本文针对文科类院校专业课程的设置特点，从教材教学内容的选择出发，融入课程相关研究领域的介绍、并找到合适的思政教育结合点，使学生更好地掌握相关算法的基本原理的同时，了解该课程在国内业界的应用前景。此外通过与数学建模知识相结合，合理设置上机实验，使学生具备一定的算法验证及设计能力，以此切实提高学生运用数学方法解决实际问题的能力。

关键词 数值计算 教学方法 教学实践

中图分类号：G424文献标识码：ADOI：10.16400/j.cnki.kjdk.2021.29.049

Practice of "Numerical computation" Course in Liberal Arts Colleges

DENG Xiaomao[1]， LIAO Ziju[2]

（[1]SchoolofMathematicsandStatistics，GuangdongUniversityofForeignStudies，Guangzhou，Guangdong510006；（[2]Department of Mathematics， Jinan University， Guangzhou， Guangdong 510632）

Abstract"Numerical computation" is a course that studies the methods and theories of solving mathematical and physics problemswithcomputerprograms.Itisanimportantandbasicintroductorycourseincomputationalmathematics.According tothecharacteristicsofmajorcoursesinliberalartscolleges，thiscoursestartsfromappropriateselectionofteachingmaterials and contents， then integrates introduction of relevant research fields， and finds some combination points of Ideological and Political Education， so that the students can better master the basic principles of relevant algorithms and understand the application prospect of the course in the domestic industry. In addition， by combining the knowledge of mathematical modeling and reasonably setting up computing experiments， students can obtain some algorithm verification and design ability and thus it can effectively improve their ability to solve practical problems by using mathematical methods.

KeywordsNumerical computation； teaching methods； teaching practice

文科类院校“数值计算”课程是应用数学系学生的专业选修课，该课程包含了计算数学方向的专业课“数值线性代数”“数值逼近”“微分方程数值解”等课程的众多经典算法。由于算法繁多而杂，公式冗长难记，学生容易将此门课程作为一门数学工具类的课程对待，满足于死记公式，而忽略掌握算法构造的原理，更不用说设计新的数值算法。由于课时数有限，课程内容难以讲解透彻，上机实验内容也难以丰富，这对授课教师在课程的设计和安排上提出了更高的要求。就如中国科学院院士、计算数学专家袁亚湘所提出，大学数学除了介绍数学的重要成果、漂亮的方法和巧妙的技巧，更重要的是介绍数学的思想。[1]如何更好地传授每个方法背后的数学思想，激发学生的学习兴趣并引导学生主动思考是每位数学教师应该着力的方向。为此，一方面教师需要对课堂教学内容精筛细选，保证算法讲解部分自成体系，[2]另一方面需要合理設置上机实验，使学生获得一定的算法实践能力。[3]笔者就以上两个方面谈自己的看法。

1教材内容的选择与取舍

在课堂教学内容的选择方面，首先对教学内容应该进行模块化分解。笔者选择的是李庆扬《数值分析》第五版的教材，但是授课时不是采用教材的原有顺序，而是将线性方程组的直接解法和迭代解法，非线性方程的求解等作为教学的第一部分，然后将插值法、函数逼近、数值积分与微分等内容作为第二部分，最后将常微分方程数值解作为第三部分进行讲解。通过教学内容的合理安排，使得知识点之间的联系更加紧密，有利于学生掌握和复习。

其次，每个重要的算法不乏相关的公式推导和定理证明，理解这些定理通常需要“线性代数”“高等数学”等课程的基础，全部讲解费时费力，故应适当选择重要的定理进行证明。比如矩阵LU分解的原理需要反复运用初等矩阵的性质，杜利特尔分解和平方根法均是基于该分解得到；拉格朗日插值的截断误差中反复使用罗尔中值定理的技巧，在牛顿插值、埃尔米特插值截断误差的证明中仍然需要用到；插值型数值积分公式对奇数个积分节点的代数精度会至少提高一阶的结论需要用到对称区间上奇函数的定积分性质；牛顿法的局部平方阶收敛性质的证明，从而说明牛顿迭代法对初值有要求，只能选取在真解附近；定常迭代法收敛定理为雅克比迭代法、高斯-赛德尔迭代法和超松弛迭代法提供了通用的收敛判断准则等，以上这些定理可详细讲解。对于一些储备知识，如矩阵算子范数的推导、对称正定矩阵的性质等，都可以在抛砖引玉的前提下分解成小的证明题，留作为课后练习，避免课堂上过多的理论推导使学生感到枯燥，还能使学生通过动笔练习获得更深的理解。高年级的学生完成作业的质量和积极性比较高，但是课本习题通常比较少，可进行一定量习题的补充，且在逐年教学的过程中可形成一定的习题库积累。

2教学实践环节的设计与探索

数值计算课程关注的是将数学模型离散成计算机可求解的模型并且快速高效求解这个过程，通常省略了实际问题的分析到数学模型的建立这个过程。通过多搜集实际应用中数学建模的例子作为算法讲解的引子，在每个算法讲解模块开始和结束时都设置一定比例的贴近学生生活及其所学专业的数学建模实例，[4]让学生明白数值计算如何应用，从而激发学生的学习兴趣。例如市场调查中用户满意度与产品质量、外观、价格等参数的关系分析中通常需要进行数据拟合，数据拟合常用的工具是最小二乘法，最小二乘法的实现通常需要求解法方程组，通过本课程正交多项式的构造可以省去对该方程组的求解；根据不同深度的海水温度数据，通过多项式插值可估计出其他深度处的水温；在金融领域隐含波动率反映了投资者对标的资产未来波动率的预期，把期权实际价格及相关参数代入期权理论价格模型如布莱克-斯科尔斯公式，通过求解一个非线性方程可反演得到隐含波动率。此处非线性方程的求解需要用到二分法、不动点迭代、牛顿法等数值方法。

此外，教师应结合自身的研究方向，给学生传达与本课程相关的最新科研进展和业界资讯。大三是学生思考未来就业及学业深造方向的重要学年，学生对所学知识的背景和应用也尤为感兴趣。本课程作为计算数学方向的介绍性课程，应让学生了解所学领域的发展趋势和应用前景，同时通过介绍国内该领域的发展，可自然地在课程中引入思政教育的内容。[5]例如近十几年来我国高速铁路的蓬勃发展，极大方便了乘客出行，促进了地区间的经济文化交流，为中华民族伟大复兴的中国梦贡献了巨大的力量。经过众多的技术创新和系统优化，中国现已成为世界高铁技术领域的佼佼者。在高铁动车组研发过程中，为减小列车高速前进时的空气阻力，同时减弱会车、进出隧道时给乘客带来的不适感，高铁列车头被设计成子弹头的流线型，此设计是通过对列车高速前进以及会车、进出隧道时进行详细的空气动力学分析得到。而众所周知气动分析通常需要借助数值仿真技术来完成，从计算数学的角度就是需要数值求解三维的Navier-Stokes流体动力学方程，与本课程微分方程的数值求解算法联系密切。此外，自2009年我国国防科技大学发布“天河一号”超级计算机，我国成为国际上第二个可以独立研制千万亿次超级计算机的国家。随后研发的“天河二号”“神威·太湖之光”“天河三号”等超级计算机均为大数据时代的应用提供了重要的硬件基础。气象学高精度数值天气预报、制造业工业设计仿真、医学图像处理及诊断等领域中数值求解大规模线性及非线性方程组的需求均可由超级计算机来完成。而线性方程组的数值求解算法是本课程的重点学习内容。通过以上两个例子，可使学生深切体会到我国在科技领域日新月异的發展，增强民族自豪感和责任感，增强“四个自信”，有助于学生树立正确的世界观、人生观和价值观。

3上机实验题的合理设计及灵活的评分机制

在实验设计方面，考虑到课时的限制，在每个模块讲解结束可设置上机实验，让学生完成实验报告并提交程序。在每次上机实验完成后，教师应仔细讲解算法的程序，针对学生编写算法过程中容易出现的程序语句过于烦琐或者程序逻辑不通等问题，适当讲授程序设计的基本原理，并从算法的存储空间和计算速度等方面对算法进行评价，使学生对数值算法的计算效率有更加深刻的认识。如在编写解线性方程组的平方根法、雅克比迭代法、高斯-赛德尔迭代法等算法时，由于MATLAB的矩阵向量运算非常方便，学生会随意地生成矩阵和向量，造成了大量存储空间的浪费。在设计数值实验时，可添加如何使得计算量最小、计算空间最省等要求，使学生深入思考算法设计和实现的过程。

此外，实验设计部分需要区分算法验证题和算法设计题。第一种实验是加深学生对于课堂所学经典算法的理解；[6]如比较不同插值方法对同一组数据的插值效果；自己编程发现高次多项式插值的龙格现象的存在；比较不同迭代法的收敛速度和不同初值所获得的解的精确度等。这类算法验证的问题可训练学生学会整理以及展示数值结果，更重要的是通过分析发现数值结果背后的规律，使之发现可能存在的问题，并思考可能的改进方法，由此过渡到新算法的设计，也即第二类题目算法设计题的要求。算法设计题还可与数学建模相结合，进一步加强学生实践和创新能力。例如：结合新冠疫情传播的现象介绍常见的传染病数学模型如SI、SIR、SEIR模型等，设置相应的算法设计及应用题目。例如，在上学期的“数值计算”课程上，我们设置了关于SEIR模型的题目，其相应的常微分方程组如下：

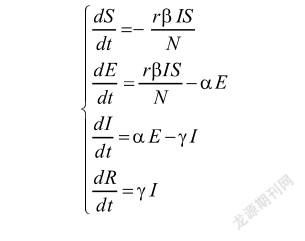
其中S，E，I，R分别表示如下各类人群的数量：

（1） S类，易感者（Susceptible），指未得病者，但缺乏免疫能力，与感染者接触后容易受到感染；

（2） E类，潜伏者（Exposed），指接触过感染者，但暂无能力传染给其他人的人，对潜伏期长的传染病适用；

（3） I类，感病者（Infectious），指染上传染病的人，可以传播给S类成员，将其变为E类或I类成员；

（2）请搜集某地区人口、新冠疫情感染人数等数据，测算传染率，康复率等参数，并将数据代入上述模型，测算出与该数据最吻合的计算模型，对模型给出合理的解释，并预测疫情的变化趋势。

第一类算法实验可让学生独立完成，鼓励使用多种语言如MATLAB、C、C++、Python等进行程序的编写，对于优秀的实验报告可以分享给学生共同学习；第二类算法实验可以分组形式完成，[7]给予学生充分的时间准备，并在课程设计中预留出课堂时间用于各组实验的PPT汇报，培养学生的协调合作能力和表达能力，教师对实验中遇到的问题和汇报内容的优缺点应及时进行合理的点评。

最后，由于上机实验是本课程必不可少的一环，为了让学生提高利用计算机进行数值计算的能力，本课程的考核方式也应符合课程的实际情况，更加灵活。[8]比如适当提高实验报告的成绩比例到总成绩的30%-40%，期末考试试卷中适当添加一些开放性的问题等。通过合理的教学内容设计和上机实验实践，使学生从本课程中了解数值算法的设计原理和实现步骤，进而有助于了解现有数值计算软件所集成的算法，并可从编程实践中获得解决实际问题的能力。

参考文献

[1]袁亚湘.大学数学重在介绍思想[J].高等数学研究，2002（5）：4-5.

[2]赵丽萍，柳炳详.《数值计算方法》课程教学改革的建议[J].办公自动化，2018（379）：41-42，60.

[3]阎少宏，刘春凤，张焕成，等.基于MATLAB的数值计算方法课程教学研究[J].科技创新导报，2014（31）：131.

[4]张建华.应用型人才培养中数值计算方法课程教学改革与实践[J].大学教育，2013（4）：51-52.

[5]李晓京，孙国辉，张超，等.以“习近平青年教育观”引领高校思政工作进入新局面[J].教育教学论坛，2021（27）：1-4.

[6]郭跟成，徐美玉，杨春蕾.阿尔伯塔大学数值计算方法课程的启示[J].现代计算机，2013（7）：30-33.

[7]金元峰，尹哲.“数值计算方法”课程教学改革探讨[J].高教研究与实践，2011（30）：57-59.

[8]朱立华.提高“自我效能”的“数值计算方法”课程形成性评价机制设计与实践[J].科教导刊，2021（11）：124-126，130.