关于抛体运动阻力渐变过程的理论推导及讨论
2021-01-13石丽芬
杨 帅,廖 周*,石丽芬
(1.乐山师范学院 数理学院,四川 乐山 614000;2.四川文化产业职业学院 大数据与互联网学院,四川 成都610000)
0 引言
抛体运动是牛顿力学中的一个重要内容,也是日常生活中的一种常见运动形式。对抛体运动的研究一般在没有大气阻力的理想情况或者有空气阻力条件下进行,但对抛体运动从稠密空气阻力到忽略大气阻力影响真空状态的运动过程的研究研究较为重要。目前对此问题的研究,大多是用泰勒公式、拉格朗日乘子法[1-3]等方法,分析一般阻力方程导出忽略空气阻力的运动方程及其性质的,却很少用根据空气变化的实际物理过程情况进行分析(如发射深空火箭过程,其受到的空气阻力就是从有渐变到无限小的过程)。本文根据牛顿力学得出抛体运动有空气阻力的一般方程,而无空气阻力的理想情况可由有空气阻力的方程简化而成,也就是无空气阻力的抛体运动规律便可由有空气阻力抛体运动的一般方程直接导出。但将空气阻力为零直接代入一般方程时,会出现方程式无意义的情况。本文为解决这一情况,从数理极限思想的角度出发让空气阻力逐步渐变为零,推导出空气阻力变化过程的抛体运动解析公式,并得到忽略大气影响理想状况的抛体运动方程可以由有空气阻力的抛体运动方程简化而来。论文最后并用Matlab做了数值仿真实验。
1 抛体运动理论推导

图1 斜抛射运动示意图
如图1所示,一抛射体在以初始速度v0抛射出,v0与平面夹角为θ。在没有空气阻力情况下,根据牛顿力学分析,并进行矢量分解,可以得到抛射体在水平(x)和竖直(y)的速度和运动方程为:
(1)
g为重力加速度。在x和y方向的位移方程为:
(2)
消除参数后得到斜抛射运动轨迹方程为:
(3)

图2 有空气阻力时的抛射运动
如图2中,如斜抛射运动有空气阻力,且阻力大小跟运动速度有关,Fr=-kv(k为比例系数,v为抛射体瞬时速度)。根据牛顿第二定律F=ma,抛射体受到的力为:
(4)
其中Frx=-kvx,Fry=-kvy为空气阻力在x和y两个方向的分解量,公式(4)为:
(5)
初始速度v0x=v0cosθ,v0y=v0sinθ,得到抛射体在有空气阻力情况下,在水平(x)和竖直(y)的速度和运动方程为:
(6)
将dx=vxdt,dy=vydt代入公式(6)得到相应位移方程为:
(7)
消去参数t后可得抛体的轨迹方程为:

(8)
公式(6)-(8)为抛体运动在有空气阻力情况下的运动方程,如果空气阻力趋于0(即k=0)时,公式(8)应简化为公式(3)。将k=0代入公式(8)中,得到的结果与公式(3)差异很大,原因是将k=0代入公式 时,公式中会出现了0/0或者无穷大情况。为了处理此问题大多是利用数学方法进行处理[1-3],但此类方法只考虑数学方法实现[4-5],缺乏合理的物理逻辑解释。本文我们从物理过程出发进行分析,在空气阻力减弱并逐渐趋于零的过程,实际就是微积分中的极限过程。因此可基于极限思维解决此问题,以下是具体推导过程。
2 物理渐变过程推导
对速度、位移和轨迹即公式(6)-(8)利用洛必达法则求极限,可以得到无空气阻力情况下的相应公式 (9)-(12)。下面对具体情况进行推导:
对速度公式中的vx可以直接将k=0代入,对于vy需要先利用洛必达法则,对分子分母求导后再求极限:

(9)

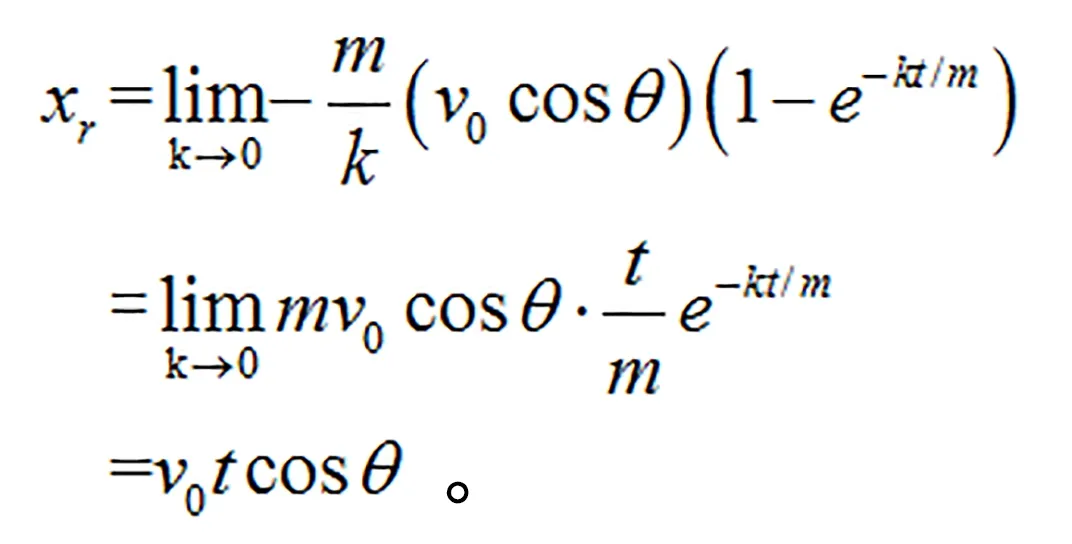
(10)
连续用两次洛必达法则,可以得到y方向的位移公式:

(11)
从推导公式(10)(11)可以看出,当k→0时,位移公式(7) 就演化为公式(2),证明了公式(1)-(3)为公式(6)-(8)的特殊情况,跟实际物理过程也吻合。

同理可以推导出忽略空气阻力的抛体运动的轨迹方程公式:
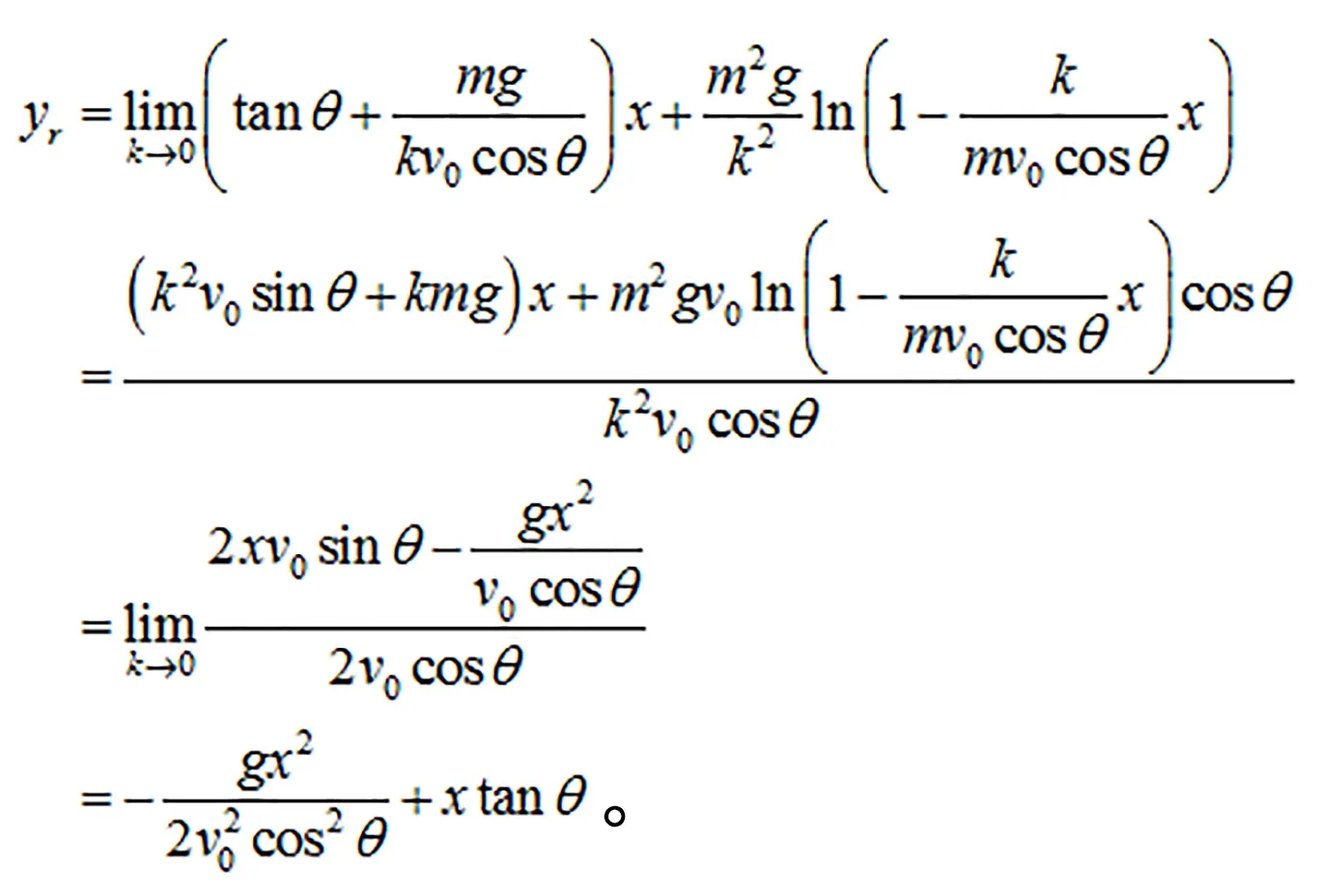
(12)

3 数值仿真
对不同的空气阻力以及不同抛射角度进行数值仿真[7],仿真输入为:设物体为球体,质量m=1kg,初始速度为v0=20m/s,重力加速度g=10m/s2,初始角度为θ=45°,空气阻力系数分别为k={0.3, 0.1 ,0.05 ,0.01, 0.001, 0}。
图3是仿真结果,其趋势跟数理推导吻合很好,在空气阻力k=0.001时曲线已经很接近真空状态了,两条曲线很接近,可以看出仿真结果论证了前面理论推导。

图3 在不同空气阻力条件下的斜抛射运动
在相同条件[6-10],去空气阻力为k=0.01,角度为θ={20°, 30°, 40° ,45°, 50° ,55°},进行数值仿真。其结果如图4所示,可看出在抛射角度θ=45°时,距离最远,验证前面推导结果。

图4 空气阻力下斜抛射运动不同角度影响
4 结 论
本文针对物体抛射运动的物理问题,基于实际物理运动的逻辑过程,利用微积分极限思想,详细推导分析了物体抛射运动从有空气阻力到真空状态的运动状况。
考虑抛射点与落地点在同一平面的情况,运用微分学知识导出存在空气阻力的一般性质再运用极限思想当阻力系数k趋近于零(k→0)时导出无空气阻力情况下的抛体运动公式与抛体性质,还将加速度与夹角α一般化得到了运动学中的一般公式。
在物理教学中,将高等数学知识与物理问题联系起来,用数学知识得到一般物理公式再将条件特殊化得到中学物理课本上的特殊公式,有利于学生理解公式意义,将会取得事半功倍的教学效果。
