基于RTDS的VSC控制参数分环拟合方法

徐鹏，米建宾，蒙小飞，谢欢

基于RTDS的VSC控制参数分环拟合方法

徐鹏1，米建宾2，蒙小飞3，谢欢2

（1．国家电网公司华北分部，北京市 西城区 100045；2．国网冀北电力有限公司电力科学研究院，北京市 西城区 100045；3．华润电力(温州)有限公司，浙江省 温州市 325000）

电压源换流器(voltage source controller，VSC)作为风电、光伏及换流站等设备的主要电力电子元器件，其控制方式和参数整定对系统运行有着重要的影响。基于实时数字仿真仪(real time digital simulator，RTDS)半实物仿真和纯数字仿真，提出一种用于拟合实际VSC控制模型参数的方法。以典型VSC并网系统模型为例，首先，借鉴锁相环原理提出一种具有自适应性观测坐标系建立方法，用于对比拟合2种仿真模型的阶跃响应；其次，分别给出了VSC锁相环、电流内环和电压外环的拟合方法，其中在电流内环控制参数拟合过程中，利用观测坐标系在控制器锁相环输出角度未知时实现电流阶跃；最后，通过不同控制环节模型参数拟合时的仿真对比分析，证明了所提方法的有效性。

电压源换流器(VSC)；参数拟合；自适应观测坐标系；锁相环(PLL)

0 引言

随着新能源发电并网、柔性直流输电工程的不断投产和扩建，电力系统中电力电子元器件的数量也在不断增加，给现代电网的稳定运行带来了新的挑战。电压源换流器(voltage source controller，VSC)[1-4]作为风电、光伏及换流站等设备的主要电力电子元器件，其控制方式和参数整定对系统运行有着重要的影响。

然而，截至目前，VSC的内部控制逻辑、参数设置等方面仍未有相关的企业标准或行业标准。受行业发展和制造工艺等因素的影响，不同厂家的VSC在参数整定和运行特性上均有较大差异，且出于企业核心机密的考虑，VSC内部逻辑参数均未公开。研究人员只能根据其外特性来粗略估计VSC的控制逻辑和参数[5-8]，据此得出的分析结果也不尽如人意。

考虑VSC的典型模型结构具有一定的通用性，因此，本文基于实时数字仿真仪(real time digital simulator，RTDS)闭环仿真系统，提出一种VSC控制参数分环拟合方法。该方法主要以锁相环(phase-locked loop，PLL)、电流内环和电压外环为对象，首先建立一种独立的观测坐标系，然后调整理论模型结构和运行工况，并在观测坐标系下通过阶跃响应实现参数拟合，从而获得实际物理控制器的整定参数，为调试研究人员提供帮助。最后，通过仿真对比验证本方法的有效性。

1 基于RTDS的VSC理论控制模型

1.1 模型简介

自加拿大McGill大学的Boon-Teck Ooi等人首次提出VSC-HVDC技术以来，VSC的拓扑结构研究一直是学术界研究的热点，基于可控关断器件和脉冲宽度调制(pulse width modulation，PWM)技术的VSC，近几年已广泛用于将可再生能源接入电网。典型的VSC并网系统一次电路结构如图1所示。

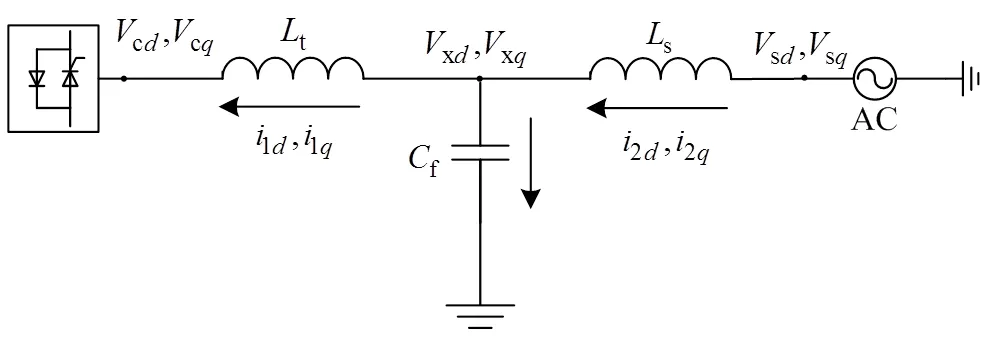
图1 VSC并网系统一次接线图

用于参数拟合的仿真模型包括半实物仿真模型和纯数字理论模型。其中，半实物仿真模型是指用实际直驱风机控制器与RTDS形成硬件闭环的仿真系统；纯数字理论模型是指在RTDS中采用经典控制模型结构搭建的纯数字仿真模型。2种模型一次结构和参数完全一致，不同之处在于：半实物仿真模型中VSC触发脉冲是由实际的物理控制器通过数据采集而生成，模型中没有二次控制环节；纯数字理论模型中包括有锁相环、电流内环和电压外环等二次模型，VSC触发脉冲是根据电流内环输出三相调制电压生成。

考虑到直驱风机并网稳定性主要受网侧VSC参数及控制方式的影响，因此，上述2种模型中对于直驱风机机侧模型进行了等效，具体等效方法与所拟合的控制环有关。本文所提出的参数拟合方法中，当对锁相环、电流环进行参数拟合时，直流侧采用“电压源等效”；当对电压环进行参数拟合时，直流侧采用“电流源等效”。用于参数拟合的仿真模型一次主电路如图2所示。

在进行锁相环、电流环、外环的参数拟合中，图2中方框内元件参数和结构保持不变。对于图2中直流侧、系统侧模型的结构和参数，则根据不同的控制环拟合而进行相应修改。

一般情况下，用于可再生能源接入电网的VSC换流器，其外环控制包括直流电压外环和无功功率外环，分别用于有功、无功功率控制；内环控制由、轴电流环构成，用于实现VSC交流侧有功、无功的解耦控制[9]；锁相环采用轴电压定向方式，实现VSC与电网电压的同步。

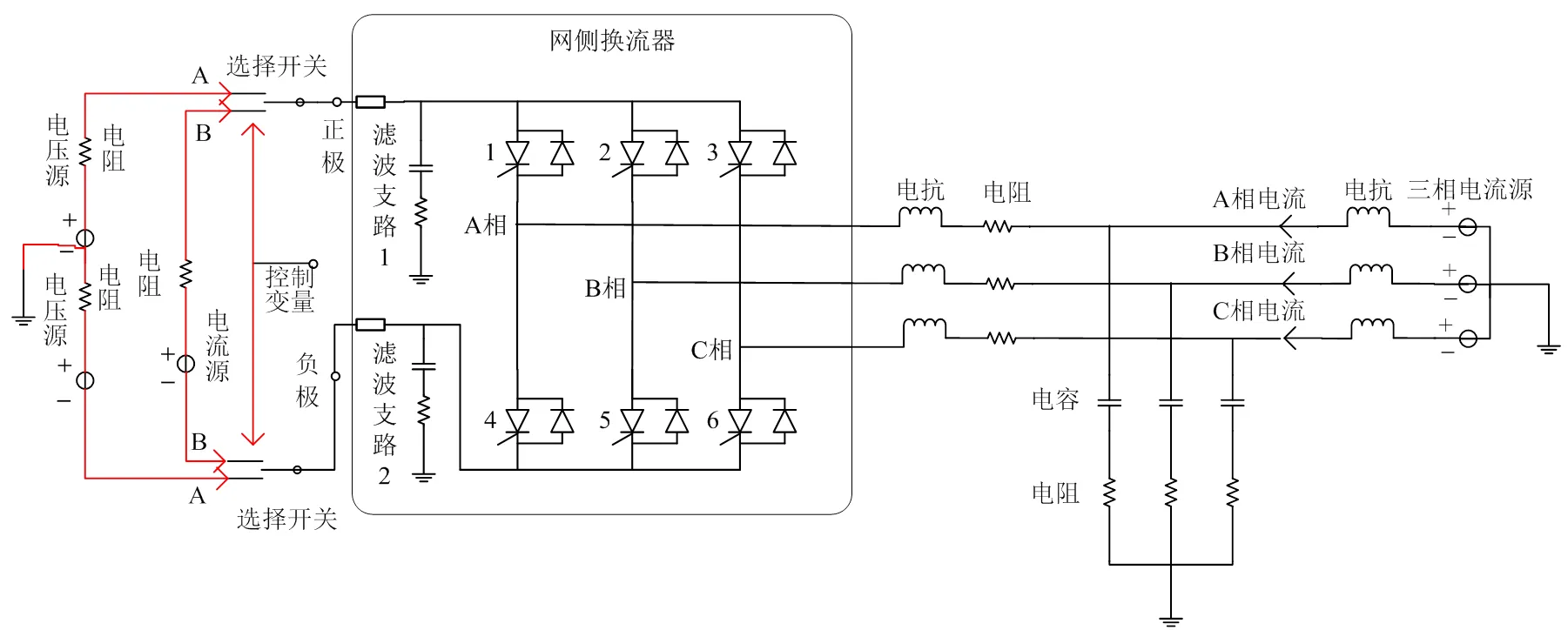
图2 VSC参数拟合仿真模型一次结构图

1.2 锁相环

作为一种常规的闭环同步方法，锁相环为控制环节提供必要的坐标变换相位角度。近几年来，二阶广义积分型锁相环(second-order generalized integrator PLL，SOGI-PLL)，改进型锁相环[10-12]等方法也引起了广泛关注。为不失一般性，本文采用三相系统中常用的同步旋转参考坐标系锁相环(synchronous reference frame PLL，SRF-PLL)，其模型结构如图3所示。

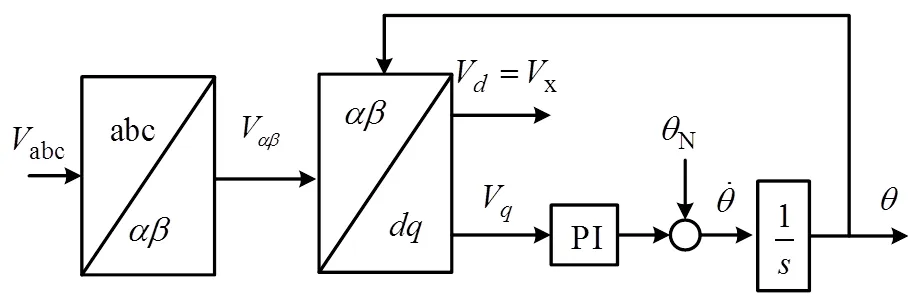
图3 三相同步旋转参考坐标系锁相环

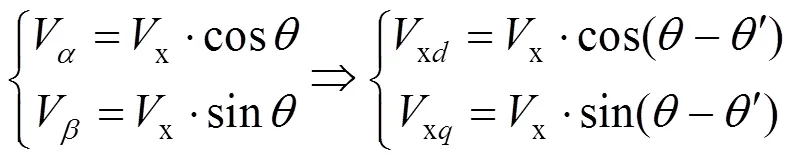
式中：表示锁相环对应dq坐标系中d轴与静止坐标a轴的夹角。各空间矢量、角度的关系如图4所示。

综上可知，锁相环输出角度与定向点电压相位和角速度有关。对于不同的仿真系统，角速度一般都取工频值(S=2pN)，而电压相位则不尽相同。且对于混合仿真模型，实际VSC控制器内的锁相环输出角度未知，难以实现其与理论模型仿真结果的对比分析。为此，本文提出了一种观测坐标系建立方法。

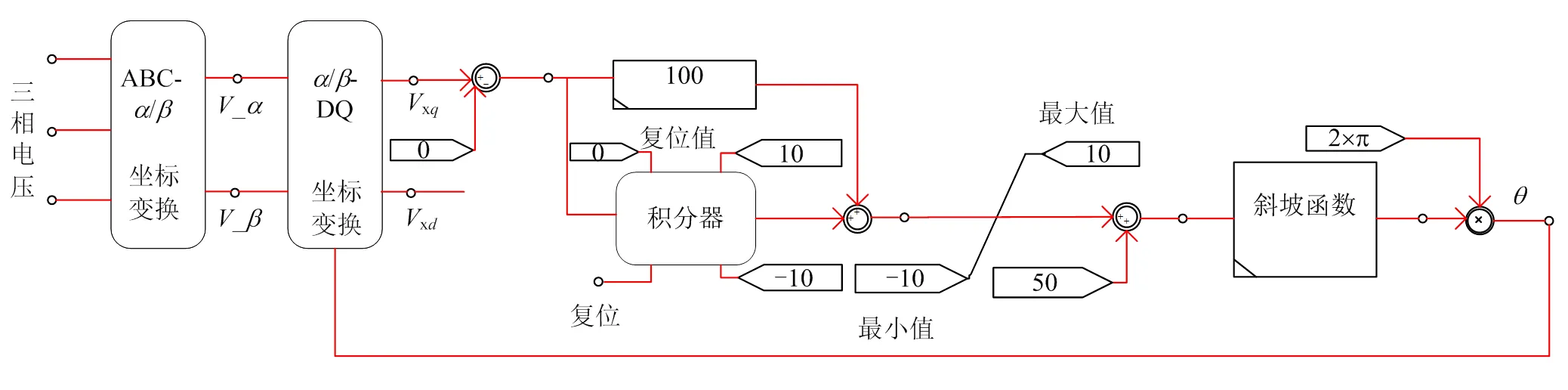
图5 PLL模型图

1.3 自适应观测坐标系模型

除了仿真系统不同以外，一般设备生产厂家的控制器没有内部锁相环输出角度的外部接口，因此，通过建立自适应观测坐标系，可以实现理论模型与实际控制器的参数拟合。本文所提出的自适应观测坐标系属于坐标系的一种，其具有以下特点：

1）系统稳定时，VSC交流侧空间电压矢量与观测坐标系的横轴重合；

3）观测坐标系利用负反馈获取坐标变换角度，不受仿真初始相位影响，具有自适应性。

观测坐标系的实现方法：1）稳态时获得一个在观测轴坐标系中能使Tq(并网点处交流电压轴分量)为零的相位偏移角；2）将该偏移角叠加到工频锯齿波中，用于计算当前仿真系统锁相环输出相位；3）锁定，并基于此建立一个以工频角速度旋转的观测坐标系。观测坐标系的模型结构如图6所示。

图6 观测轴模型结构图

由图6可以看出，观测坐标系类似于一个独立的锁相环，而与传统锁相环不同的是，只是用于使观测坐标系与锁相环对应的坐标系在稳态时重合，而当并网点电压发生变化时，观测坐标系的旋转速度和相位不变。当在理论模型和混合仿真模型中均设立同样一个观测坐标系时，就可以在不影响各控制环节的前提下，实现理论模型与混合仿真模型相应控制环节的参数拟合，完成各系统电气量的对比分析。

1.4 电流环

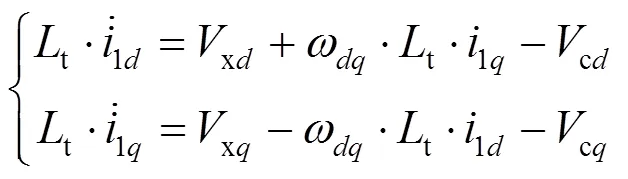
从式(2)不难看出，VSC交流侧的轴电流存在交叉耦合项，为实现VSC交流侧的有功与无功解耦控制[13]，令VSC电流环输出的、轴电压如下所示：

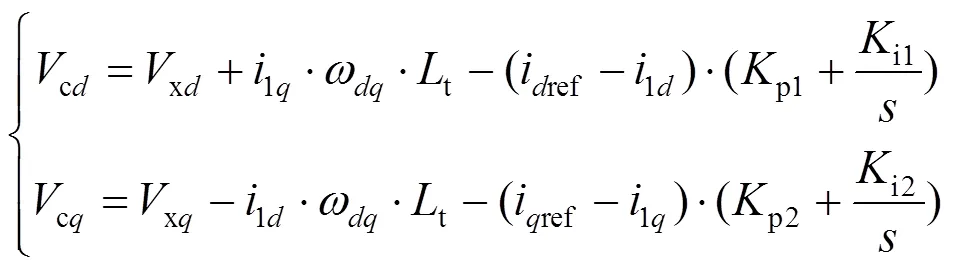
根据式(3)，在RTDS中搭建电流环控制模型如图7所示。

在混合仿真模型中，由于电流环与功率外环结合在一起，不能像理论模型那样可以直接通过改变电流给定值实现电流环阶跃响应。因此，若要完成混合仿真模型和理论模型的电流环控制参数拟合，需要采取以下2方面的措施：

1）2个仿真系统中引入一个相同的电流阶跃信号。

2）对2个仿真系统中的直流侧模型进行统一修改，以达到在实现电流环阶跃响应时去掉电压外环影响的目的。

对于第1个措施，可借助提出并建立的观测坐标系，在模型中继续搭建用于生成电流阶跃量的模型，如图8所示。

图8中，调整Ioffset、Ioffset可以改变电流阶跃量在观测坐标系中、轴上的分量。在混合仿真模型和理论仿真模型中，观测坐标系对应的并不一定相等，但只要2个模型中设置同样的Ioffset、Ioffset，则由图8生成的电流阶跃扰动量在观测坐标系上对应的、轴分量是相等的。

通过如图9所示的介入方式将电流阶跃扰动量与交流侧电流测量值叠加，然后利用锁相环输出角度进行Park变换，最后得到添加扰动后的电流环、轴输入值2d、2q。

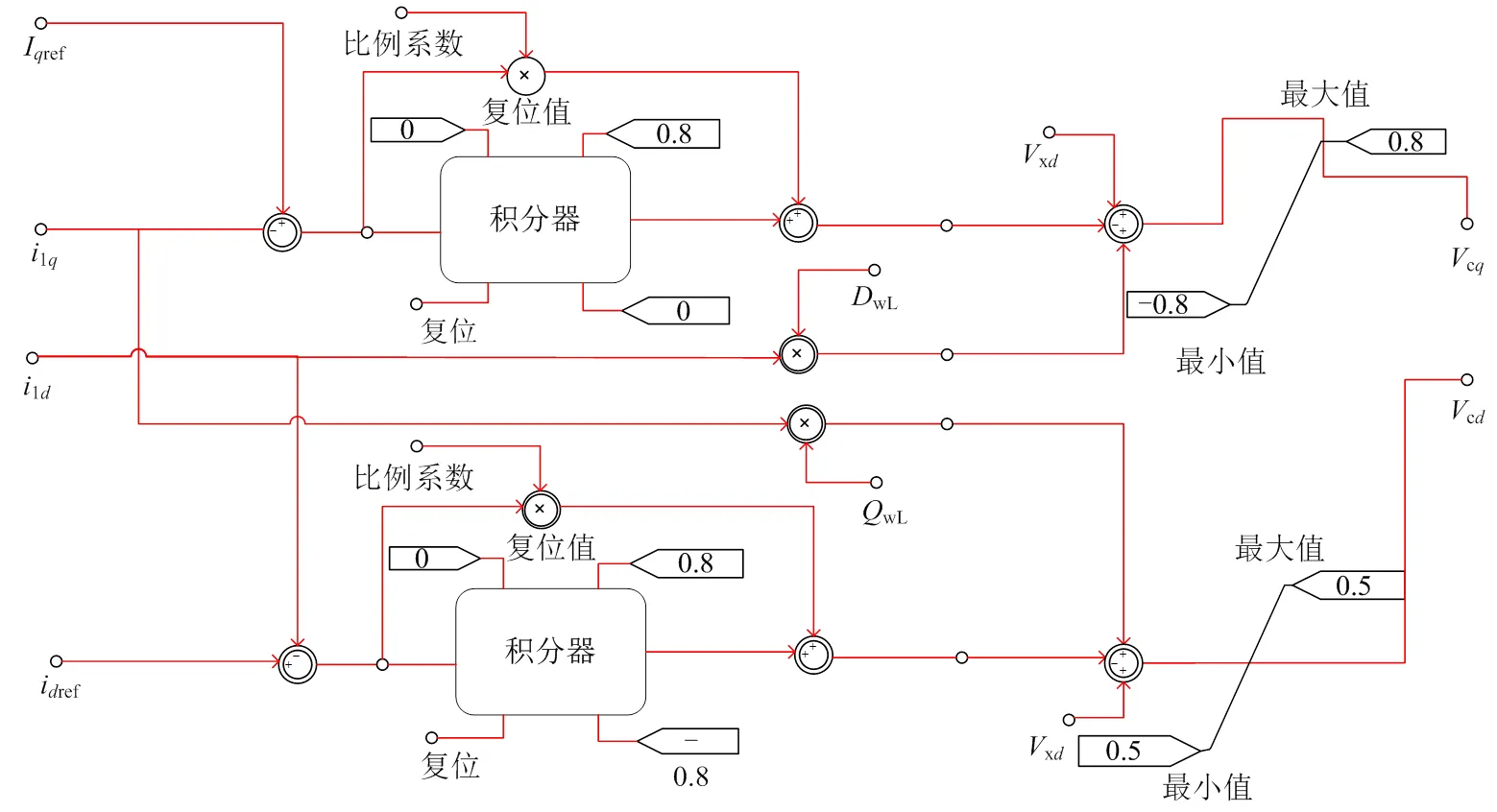
图7 电流内环解耦控制模型

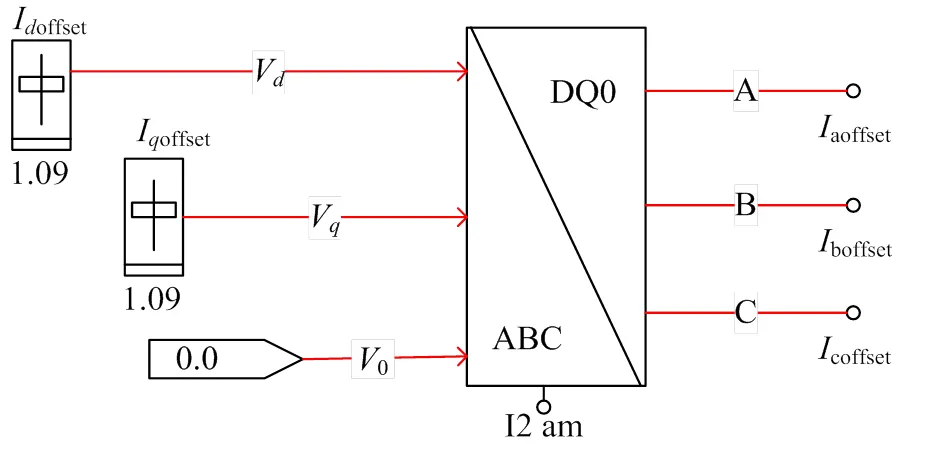
图8 生成电流阶跃扰动信号模型图

图9所示电流扰动信号的介入方式，实际上是通过改变交流侧电流的测量值而实现电流阶跃的。需要注意的是，在系统稳定点处，当叠加的阶跃量大于零时，表示实测值大于给定值，故在电流环产生的是一个“下阶跃”的响应，如图10所示。

1.5 电压外环

前已述及，本文所提出的参数拟合方法主要针对网侧逆变器，因此在电压外环参数拟合的仿真建模中，用等效电流源(电压源串联大电阻的形式)替代直流侧模型，即设置图1所示一次模型中的控制变量“modeSel”为1。电压外环控制模型如图11所示。

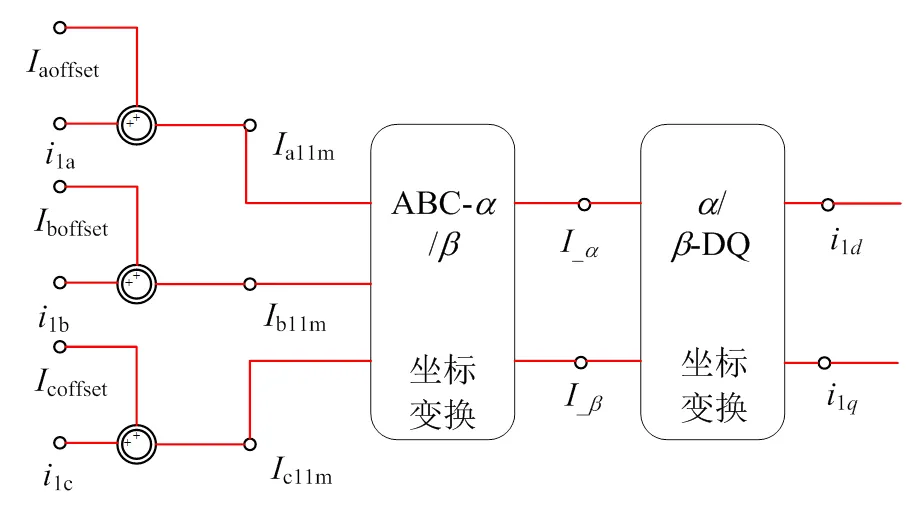
图9 电流扰动信号的介入方式

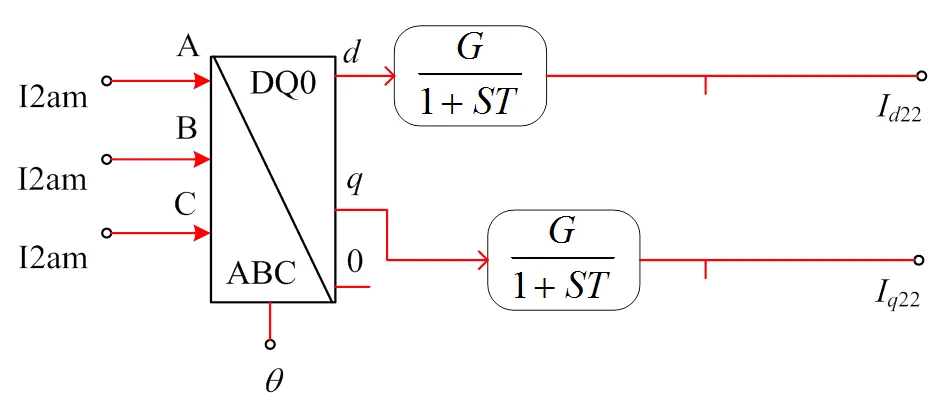
图10 电流扰动阶跃响应的观测量

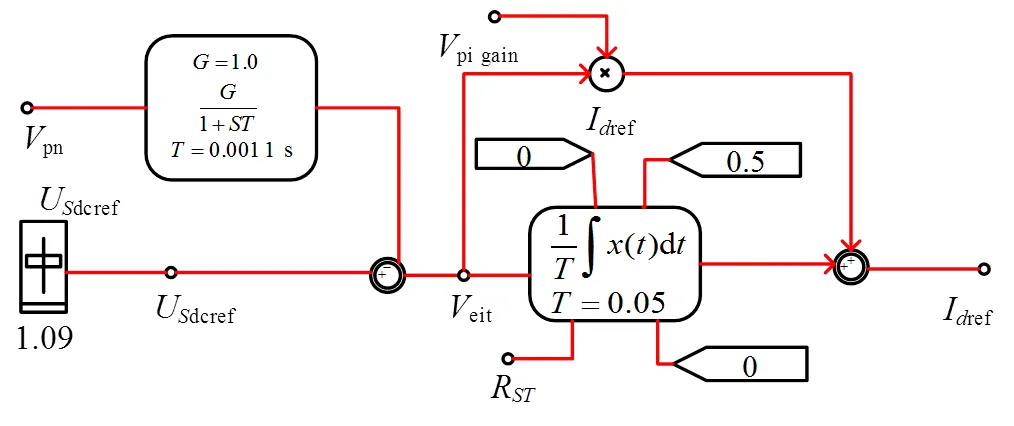
图11 直流电压外环控制模型图

1.6 无功外环

为利于VSC并网的稳定性，实际网侧逆变器的无功外环PI控制中比例、积分增益一般取值较小，甚至有的直驱风机厂家的控制器中无功外环只有一个较大时间常数(=5min)的积分环节，即无功外环相比其他控制环节的参数取值范围较大。且考虑到无功外环的参数拟合模型及方法与直流电压外环的拟合过程类似，故在此不再赘述。

2 参数拟合仿真分析

根据前述针对VSC不同控制环节的模型参数拟合方法，结合建立的观测轴坐标系，并通过不同的实验方案分别对锁相环、电流内环和电压外环进行参数拟合，实现理论仿真模型和实际物理控制器的各控制环模型参数的仿真对比。

本节中给出的所有仿真对比结果中，黑色、红色曲线分别代表理论仿真模型和实际物理控制器。

2.1 锁相环参数拟合仿真分析

在对锁相环进行参数拟合时的试验方案如表1所示。

对应一次模型结构如图1所示，控制变量“modeSel”设置为“0”，可以忽略电压外环的影响；交流侧电感按短路容量比CR=15进行取值。在进行阶跃试验时，通过调整锁相环PI参数，得到理论模型与混合仿真模型的对比结果如图12所示。其中，I11、I11表示并网逆变器交流侧电流在观测坐标系上的、轴分量；Td、Tq表示并网点电压在观测坐标系上的、轴分量。

表1 锁相环参数拟合试验方案

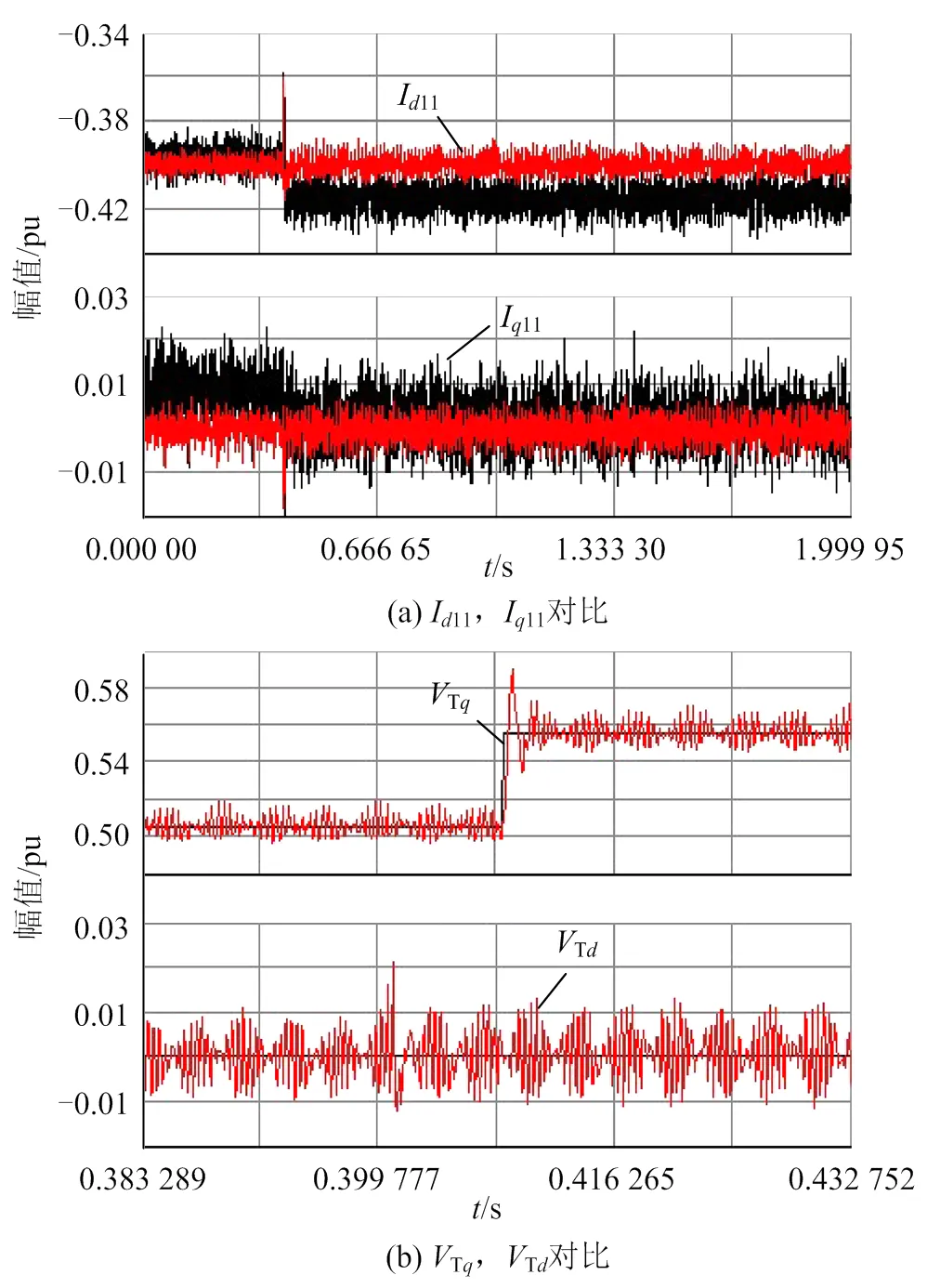
图12 等值交流电压源幅值10%上阶跃仿真结果对比

2.2 电流环参数拟合仿真分析

在对电流内环进行参数拟合时的试验方案如表2所示。

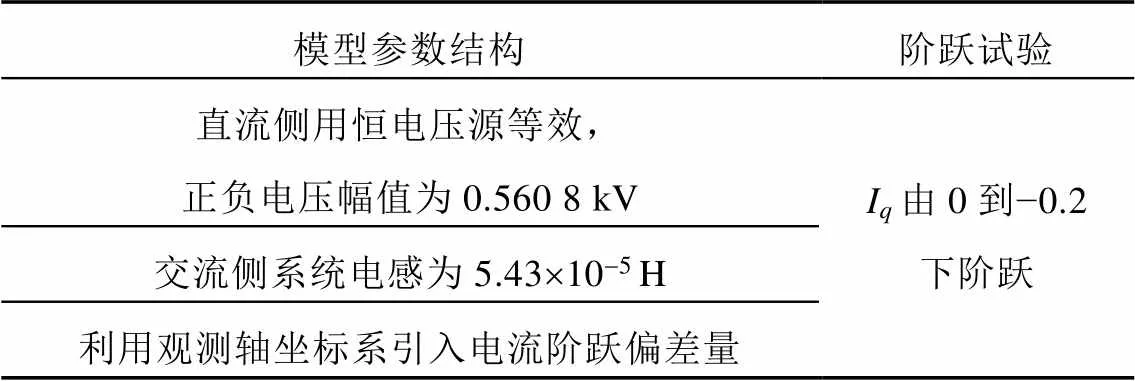
表2 电流环参数拟合试验方案

与锁相环拟合类似，为忽略电压外环对电流内环参数拟合的影响，一次模型结构中直流侧仍用恒压源等效。利用图7所示的电流测量环节，通过电流阶跃响应完成电流内环模型参数拟合。通过参数调整得到理论模型与混合仿真模型的对比结果如图13所示。

图13 Iq由0到-0.2下阶跃仿真结果对比

2.3 电压外环参数拟合仿真分析

在对电压外环进行参数拟合时的试验方案如表3所示。

表3 电压外环参数拟合试验方案

通过改变直流侧等效电流源中电压源幅值的大小，改变直流侧并联电容的充电电流，从而间接引起直流电压的变化，直流电压误差量经电压外环闭环控制后的直流电压响应可用于拟合该环节模型参数。通过参数调整得到的仿真结果如 图14所示。

3 结论

根据实际生产和科学研究的需要，提出了一套用于VSC模型参数拟合的仿真分析方法，包括自适应型观测轴坐标系建模、分环拟合时对应的一次模型结构调整等。该方法利用RTDS数字仿真与半实物仿真的对比分析，实现了对网侧VSC实际控制器内部未知控制参数的参数拟合，为进一步分析逆变侧VSC并网稳态性提供参考。通过各控制环节的参数拟合仿真分析，证明了该方法的可行性和有效性。

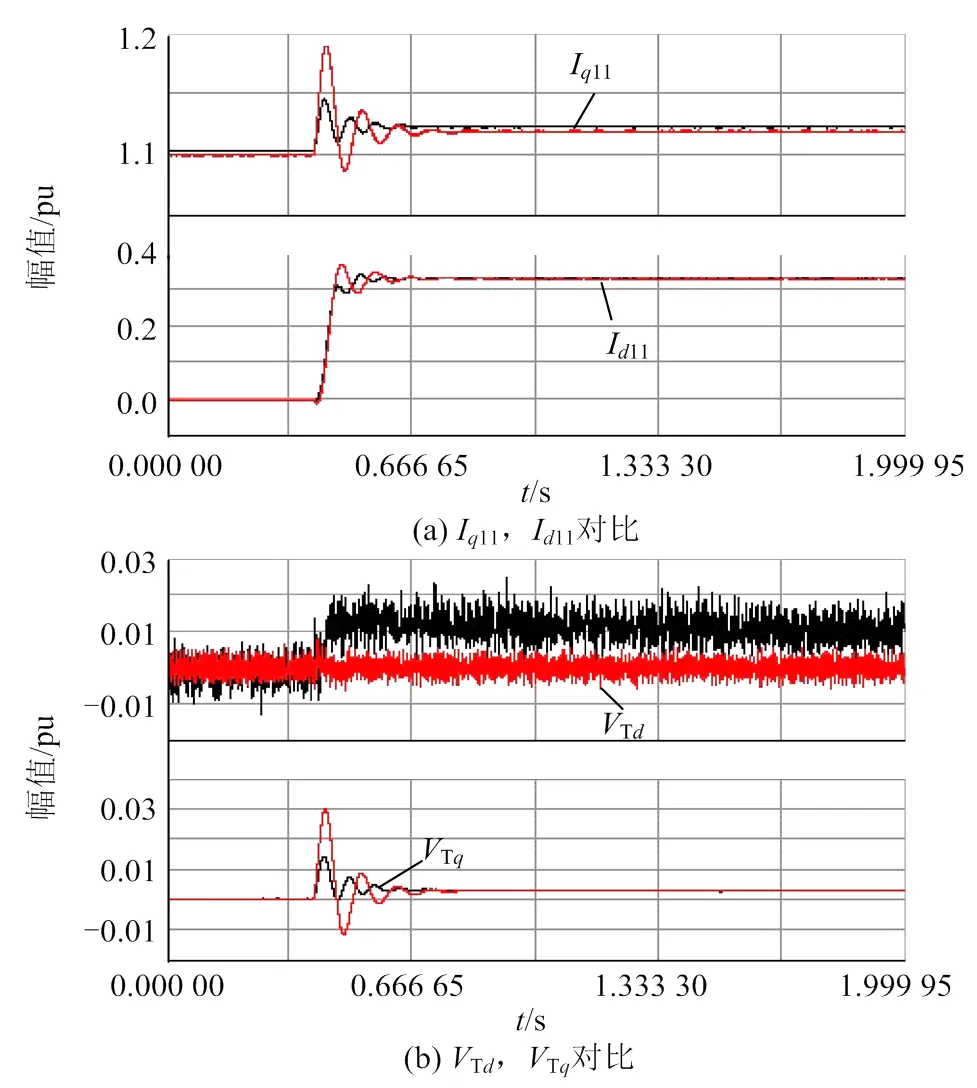
图14 直流侧电流由0到0.3阶跃仿真结果对比

[1]WU R，WEN J L，YU K S，et al．Power loss modeling of switching devices in voltage source converters

[J]．Proceedings of the CSEE，2012，32(21)：1-7．

[2]GAO R，JIA F M，LIAO Y H．Recent development of voltage source converter technology and its application to FACTS[J]．High Votage Apparatus，2016，52(11)：10-17．

[3]吴明哲，陈武晖．VSC-HVDC稳定控制研究[J]．发电技术，2019，40(1)：28-39．

WU M Z，CHEN W H．Overview of research on stability and control of VSC-HVDC[J]．Power Generation Technology，2019，40(1)：28-39．

[4]李英彪，梁军，吴广禄，等．多电压等级直流电力系统发展与挑战[J]．发电技术，2018，39(2)：118-128．

LI Y B，LIANG J，WU G L，et al．Development and challenge of dc power system with different voltage levels[J]．Power Generation Technology，2018，39(2)：118-128．

[5]沈阳武，葛云霞，崔挺，等．基于阻抗比判据的永磁直驱风力发电系统并网稳定分析方法[J]．电力系统保护与控制，2017，45(18)：45-53．

SHEN Y W，GE Y X，CUI T，et al．A stability analysis method for the gird-connected permanent magnet synchronous generator based on impedance ratio criterions[J]．Power System Protection and Control，2017，45(18)：45-53．

[6]苏咏梅，王振宇，易善明．不同风力发电机组同时并网稳定性分析[J]．电力系统保护与控制，2017，45(6)：101-107．

SU Y M，WANG Z Y，YI S M. Stability analysis for wind power integration with different WTGS[J]．Power System Protection and Control，2017，45(6)：101-107．

[7]余秀月，宋少群，郭瑞鹏，等．含电压源换流器的交直流混联电网无功优化模型[J]．电力系统保护与控制，2017，45(19)：148-153．

YU X Y，SONG S Q，GUO R P．Optimal reactive power flow model for AC/DC hybrid power grid with voltage source converters[J]．Power System Protection and Control，2017，45(19)：148-153．

[8]张兴，张崇巍．PWM整流器及其控制[M]．北京：机械工业出版社，2012：115．

ZHANG X，ZHANG C W．PWM rectifier and its control[M]．Beijing：China Machine PRESS，2012：115．

[9]ZHU H，XI X，LI Y D．PI type dynamic decoupling control scheme for PMSM high speed operation[C]//Proceeding of the Applied Power Electronics Conference and Exposition(APEC)，Palm Springs，CA：IEEE，2010：1736-1739．

[10]KARIMI M G，IRAVANI M R．A new phase-locked loop (PLL) system[C]//44th IEEE Midwest Symposium on Circuits and Systems (MWSCAS)，2001：421-424．

[11]KARIMI M G，IRAVANI M R．A nonlinear adaptive filter for online signal analysis in power systems：applications[J]．IEEE Transactions on Power Delivery，2002，17(2)：617-622．

[12]ZHU C Y，SHI L，LI X P，et al．Lock threshold deterioration induced by antenna vibration and signal coupling effects in hypersonic vehicle carrier tracking system of Ka band[J]．Chinese Journal of Aeronautics，2018，31(4)：776-781．

[13]周克亮，王政，徐青山．光伏与风力发电系统并网变换器[M]．北京：机械工业出版社，2012：128．

ZHOU K L，WANG Z，XU Q S．Grid-connected converters for photovoltaic and wind power generation systems[M]．Beijing：China Machine PRESS，2012：128．

Sub-parts Control Parameter Fitting Method of VSC Based on RTDS

XU Peng1, MI Jianbin2, MENG Xiaofei3, XIE Huan2

(1.North China Branch of State Grid Corporation of China, Xicheng District, Beijing 100045, China; 2. Electric Power Research Institute of State Grid Jibei Electric Power Company Limited, Xicheng District, Beijing 100045, China; 3.Huarun Power (Wenzhou) Co., Ltd., Wenzhou 325000, Zhejiang Province, China)

Voltage source converter (VSC) is the main power electronic components of wind power, photovoltaic and converter stations. It’s control mode and parameter setting have important influence on system operation. Based on real time digital simulator (RTDS) hardware-in-loop simulation and digital simulation, a new method of parameter fitting applied to characterize physical VSC was proposed. Taking a typical single VSC grid connected system model as an example, firstly, based on the principle of phase-locked loop (PLL), an adaptive observation coordinate system was proposed to compare and fit the step response of two simulation models. Then the fitting methods of PLL, current inner loop and DC voltage outer loop in VSC control system were introduced separately. Self-adaptive observational coordinate system was used in the process of current inner loop parameter fitting. Finally, the efficiency of the proposed method was verified by the comparative analysis of simulations.

voltage source controller (VSC); parameter fitting; self-adaptive observation coordinate system;phase-lockedloop (PLL)

10.12096/j.2096-4528.pgt.19079

TK 01; TM 461

国家重点研发计划项目(2016YFB0900502)；国家电网公司科技项目(520101180002)。

Project Supported by National Key Research and Development Program of China (2016YFB0900502); Science and Technology Program of State Grid Corporation (520101180002).

2020-05-17。

(责任编辑 辛培裕)