一种涉及大地坐标的大角度三维坐标转换方法

马 雷 邵先锋 杨泰朋

(国网安徽省电力有限公司建设分公司，安徽 合肥 230022)

1 概述

坐标转换参数求解作为经典大地测量问题，通常基于七参数模型求解出不同坐标系之间的转换参数[1]。三维坐标转换的7个参数包含3个平移参数、1个尺度参数以及3个旋转参数，而精确并可靠地估计转换参数是三维坐标转换的核心问题[2]。通常利用3个及以上的公共点的坐标，将七参数模型转换为经典最小二乘理论的Gauss-Markov模型进行求解，然后根据求解的转换参数再将非公共点的坐标转换到目标坐标系下[3]。

当旋转角较小且尺度比接近1时，常采用Bursa-Wolf模型进行描述。当旋转角较大时，应采用相似变换Helmert模型。姚宜宾采用Taylor级数对Helmert模型进行线性化，提出了适用于大角度和任意尺度比的转换方法[4]。陈义根据旋转矩阵的正交特征，构建了附有约束的坐标转换模型[5]。另外，空间坐标的表现形式有很多种，最常见的形式是空间直角坐标系。但在某些领域的原始坐标观测值常采用大地坐标的形式，比如三维点云数据、导航数据等。当存在大地坐标时，常用的方法是将公共点的大地坐标变换为同坐标系下的直角坐标，然后利用两套直角坐标进行转换参数的求解[6]。在上述过程中，大地坐标可以很容易变换成相应的直角坐标，但是由于转换过程是非线性的，点位精度的损失难以避免。因此，在存在大地坐标的情况下，传统方法存在一定的缺陷，因此，如何避免大地坐标变换成直角坐标的精度损失具有重要的理论研究意义。

综上所述，本文以涉及大地坐标时的坐标转换为研究对象，研究混合大地坐标与直角坐标进行坐标转换的转换算法，避免大地坐标变换相应直角坐标产生的精度损失，进而提高坐标转换的精度。

2 涉及大地坐标的转换方法

大地坐标与直角坐标之间具有如下函数关系：

(1)

式中：X，Y，Z——点位直角坐标；

B，L，H——点位的大地纬度、大地精度及大地高；

N——椭球卯酉圈曲率半径；

o——椭球第一偏心率。

根据Helmert转换模型，涉及大地坐标时，对于单个点的观测方程表达如下：

(2)

式中：下标“T”和“C”——目标坐标系和源坐标系；

e——相应的随机误差项；

ΔX,ΔY,ΔZ——平移参数；

s——尺度参数；

R——旋转矩阵，具体形式如下：

R=R(εz)R(εy)R(εx);

根据Taylor级数对式(2)进行展开可得：

(3)

其中：

将式(3)整理可得误差方程：

l+Je=Adβ

(4)

其中：

当有n个公共点时，根据式(4)构建误差方程，根据经典最小二乘的Gauss-Markov模型，转换参数的最小二乘解为：

dβ=(ATPA)-1ATPl

(5)

其中，P=(JQJT)-1，Q为误差的先验协因数矩阵。

3 仿真实验

假设有15个点，选取其中10个点作为公共点，剩余5个点作为检核点。

转换参数的真值设定为：β=[1 000 m 896 m 956 m 1.3 0.046 rad -0.032 rad -0.065 rad]T。以CSCG2000椭球为例，在[-π π],[-0.45π 0.45π]以及[20 m 600 m]范围分别生成目标框架下的纬度、经度和大地高，根据Helmert转换模型的逆变换生成源框架下的三维直角坐标。在[1.5 3]×10-7范围内生成经纬度的标准差，在[1 m 5 m]范围内生成大地高的标准差(见图1)。

执行1 000次Monte Carlo实验，每次实验的参数真值和坐标是固定的，但每次实验的随机误差是通过上述的标准差采用零均值高斯分布独立生成，分别采用以下两种方法求解：

1)传统方法；

2)本文提出的直接采用大地坐标进行解算。

根据不同方案的计算结果，分别计算转换七参数以及5个非公共点在目标框架下三维坐标的RMS，具体计算公式如下：

(6)

转换参数的均方根误差见表1。非公共点解算的差值序列统计见表2。

表1 转换参数的均方根误差

表2 非公共点解算的差值序列统计

根据表1，表2以及图2可以发现：

1)在转换参数求解方面，两种求解方法的精度都较高。但相比之下，直接采用大地坐标进行坐标转换的方案2与传统方法的方案1相比，平移、尺度和旋转参数的RMS分别提高23%，28%，19%，15%，27%，10%以及8%。

2)在5个非公共站的转换精度方面，相比较于方案2，在X方向上最大值、最小值以及均方根误差平均提高11%，23%以及16%；在Y方向上最大值、最小值以及均方根误差平均提高26%，17%以及24%；在Z方向上最大值、最小值以及均方根误差平均提高23%，14%以及16%。

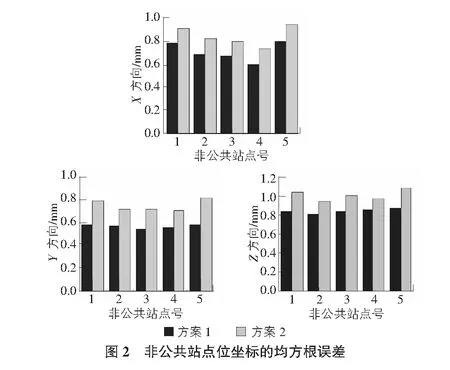
通过上述分析1 000次Monte Carlo实验的结果表明：直接采用大地坐标的方法获得结果均优于传统方法，验证了在大地坐标变换为直角坐标时，由于非线性影响导致点位精度传播时出现了损失，导致转换参数以及非公共点的转换的精度降低。因此，当涉及大地坐标时，应采用本文提出的方法进行求解。

4 结语

由于大地坐标变换为同框架下的直角坐标时，点位精度的传播受非线性影响较大，导致点位精度出现损失。本文提出的直接采用大地坐标进行转换参数求解方法，相比较于传统方法，转换参数的精度以及非公共站的转换精度都优于传统方法。另外，本文方法的理论依据是经典最小二乘的Gauss-Markov模型，通过本文推导的公式可以发现，系数矩阵A中也是存在大地坐标观测值，但该部分的误差并未考虑。因此，针对系数矩阵含有的观测值需要采用整体最小二乘的思想进行进一步研究。