梯度结构对Ti6Al4V表面Nb2O5/Nb2O5-Ti/Ti多层涂层残余热应力的影响

单湘衡，李文元，张海波，丁一帆，丁泽良

（湖南工业大学 机械工程学院，湖南 株洲 412007）

0 引言

医用钛合金Ti6Al4V 在耐腐蚀性、耐磨性、生物相容性和力学性能等方面具有良好的综合性能，是目前医用植入体的首选材料[1-2]。但是，随着植入时间的延长，Ti6Al4V 会因为体液腐蚀而释放出有毒的金属离子[3]。因此，在Ti6Al4V 表面沉积耐腐涂层意义重大。Nb2O5涂层在耐腐蚀性、耐磨损和生物相容性等方面具有优异的综合性能[4-6]，作为植入材料的表面改性涂层，具有得天独厚的优势。但是，Ti6Al4V 和Nb2O5的物性参数相差较大，若Nb2O5直接沉积在Ti6Al4V 表面，两者的结合界面会产生较大的残余热应力[7]，导致涂层附着力减小，并且会发生开裂、脱落等现象。

功能梯度材料（functionally graded materials，FGM）是由两种或多种材料成分组合而成的复合材料，其组成、结构和性能沿某一方向发生连续变化[8]。梯度中间层可以使基体到涂层之间的成分呈现连续变化，缓解基体与涂层之间的性能失配[9-11]，降低界面应力，从而提高涂层和基体之间的结合强度。为了使梯度涂层具有最佳的结合性能，同时减小涂层的制备工作量，在涂层制备前，对梯度涂层的残余热应力进行分析并对其结构参数进行优化非常重要。

本文拟运用ANSYS14.0 有限元分析软件，对Ti6Al4V 表面Nb2O5/Nb2O5-Ti/Ti 多层涂层的残余热应力进行研究，分析中间梯度层Nb2O5-Ti 的层数与厚度、成分分布指数等对多层涂层残余热应力的影响，并且采用正交试验法对这些参数进行优化，以期为医用钛基植入材料表面改性涂层的设计与制备提供一定的理论参考。

1 分析模型

1.1 几何模型及有限元划分

Ti6Al4V 表面Nb2O5/Nb2O5-Ti/Ti 多层涂层的几何模型采用圆柱体模型，如图1a 所示。Ti6Al4V 基体的厚度和半径均为25 μm，基体表面涂层的总厚度为H（包含厚度为0.5 μm 的Ti 黏结层，厚度为h 的Nb2O5-Ti 梯度层和厚度为3 μm 的Nb2O5表面层）。考虑到模型的几何对称性和边界条件的对称性，为了节约计算时间，将其简化为二维模型进行分析，如图1 b 所示。

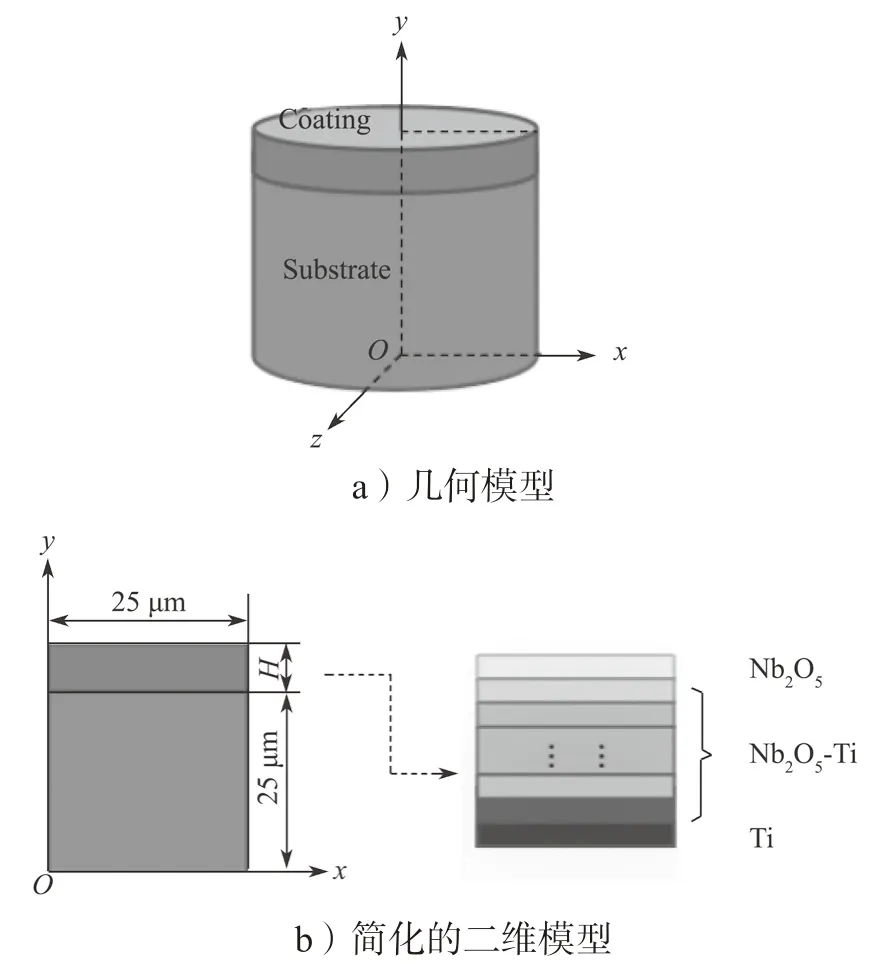
图1 模型示意图Fig.1 A model diagram

采用Plane13 单元对模型进行网格划分。由于涂层/基体结合界面附近区域的应力集中现象较为严重，故划分网格时需对该区域进行细化，直至结果的变化微小。图2 为有限元网格划分模型。

1.2 边界条件

对有限元模型的左侧（对应于圆柱的轴线）施加约束，其余3 边在热载荷作用下可自由伸缩。在分析过程中，采用如下假设：

1）分析模型为完全弹性，无塑性变形，而且材料为各向同性；

图2 网格划分模型Fig.2 Mesh division model

2）模型中的温度分布均匀；

3）材料的物理性能参数不随温度变化；

4）涂层界面结合良好，无相对滑动。

涂层制备时的基底温度t1为70 ℃，冷却后的温度t2为25 ℃，温差Δ=t1-t2为45 ℃。由于涂层与基体的热膨胀系数不同，Δ 的存在会使得涂层/基体结合界面产生残余热应力。

1.3 材料的物性参数

基底材料Ti6Al4V 和涂层材料Nb2O5、Ti 的热物理性能参数[12-14]如表1 所示。

表1 材料的热物理性能参数Table 1 Thermophysical properties of materials

梯度层材料的弹性模量E、泊松比μ、导热率λ可采用如下线性混合方式进行计算[15]：

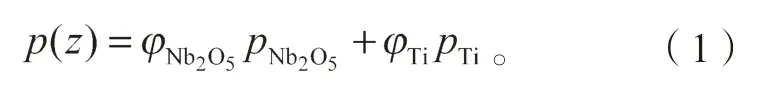
式中：p(z)为梯度层材料的物性参数；

梯度层材料的体积分数采用如下幂函数表示[16]：

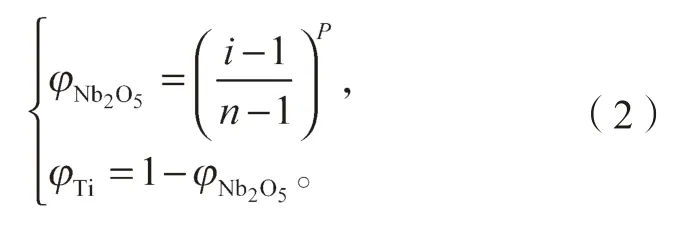
式中：P 为梯度层的成分分布指数；

n 为涂层总数；

i 为第i 个涂层，取值范围为1～n。

图3 为不同成分分布指数下的梯度层中Nb2O5组元的体积分数与所在梯度层的关系曲线。

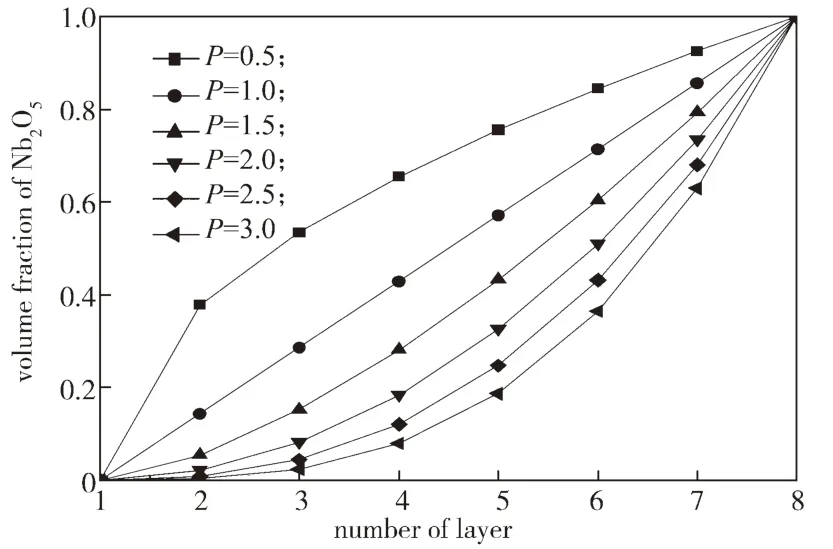
图3 Nb2O5 在梯度层中的体积分数Fig.3 Volume fraction of Nb2O5 in the gradient interlayers

由图3 可知，P＜1 时，曲线上凸，表示靠近黏接层Mg 的梯度层中Nb2O5的含量增加较快，如图中P为0.5 时，梯度层第3 层中的Nb2O5体积分数达到了54%。P＞1 时，曲线下凹，表示靠近涂层表面的梯度层中的Nb2O5含量增长较快。如图中P 为2.0 时，梯度层第6 层中Nb2O5的体积分数为37%，而第8 层则达到了100%。过大和过小的P 值都会造成涂层中某种成分含量的快速增加和梯度加大，导致涂层中出现较大的残余热应力。因此，根据涂层成分的组成，选择合适的P 值非常重要。

复合材料的热膨胀系数使用Turner 公式计算，其表达式为[17]

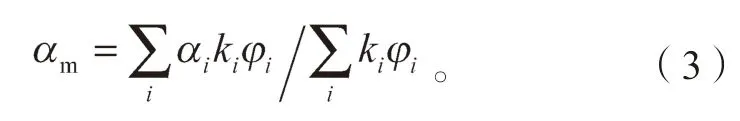
式中：αm为复合材料的平均热膨胀系数；

αi、ki、φi则为梯度材料中各组元的热膨胀系数、体积弹性模量和体积分数。

2 结果与讨论

2.1 梯度层层数对残余应力的影响

设梯度层的成分分布指数P 为1，梯度层的总厚度为2.5 μm，且各层的厚度相等，得到图4 所示多层涂层的Von Mises 等效残余热应力（以下简称残余热应力）最大值随梯度层层数的变化曲线。

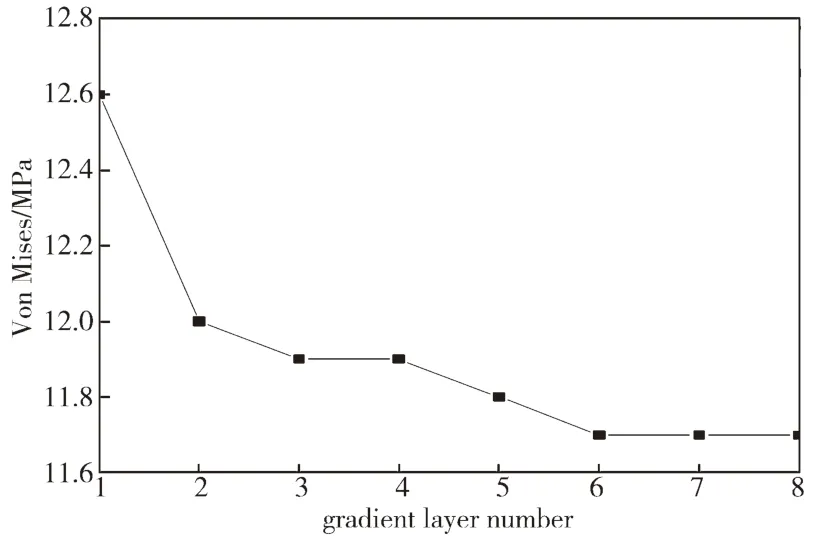
图4 梯度层层数对残余热应力最大值的影响Fig.4 Effects of the number of gradient layers on the maximum value of residual stress

由图4 可知，随着梯度层Nb2O5-Ti 的层数由1层增加到6 层，其残余热应力最大值由12.6 MPa 减小到11.7 MPa，降幅为7.1%；但是，当层数继续增加到8 层时，残余热应力最大值没有变化。这一变化特点与文献[18]的研究结论一致。由于梯度层的层数越多，涂层的制备难度越大，制造成本越高。因此，应在满足涂层性能的前提下，尽量选用小的梯度层数，因此后续实验中选择梯度层层数为6。

2.2 梯度层厚度对残余热应力的影响

设成分分布指数P 为1.0，梯度层的层数为6，各梯度层厚度相等，每层的厚度为0.2～2.0 μm。图5为残余热应力最大值随梯度层单层厚度（以下简称梯度层厚度）的变化曲线。

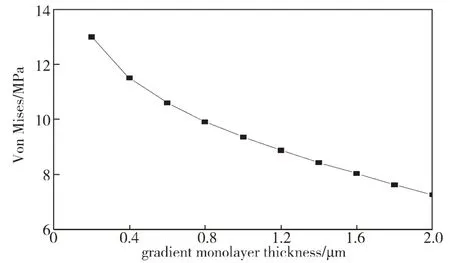
图5 梯度层厚度对残余热应力最大值的影响Fig.5 Effects of the thickness of gradient layers on the maximum value of residual stress

由图5 可以得知，随着梯度层厚度的增大，涂层的最大残余热应力最大值逐渐减小；但是梯度层厚度增大，涂层的残余热应力最大值的下降速率降低。其中，梯度层厚度由0.2 μm 增加到1.0 μm 时，涂层最大残余热应力由13 MPa 减小到9.4 MPa，下降速率为4.5 MPa/μm；而厚度由1.0 μm 增大到2.0 μm 时，涂层最大残余热应力由9.4 MPa 减小到7.26 MPa，下降速率为2.14 MPa/μm。

由于过厚的梯度层会使涂层发生弯曲效应，改变残余应力的分布，导致涂层体系综合力学性能降低，并大大增加制作时间和制造成本[19]。因此，合适的涂层厚度需兼顾性能与成本之间的关系。

2.3 成分分布指数对残余热应力的影响

设梯度层厚度为1 μm，梯度层层数为6，成分分布指数P 值取0.5, 1.0, 1.5, 2.0, 2.5, 3.0，得到图6所示的P 值对梯度涂层残余热应力的影响曲线。

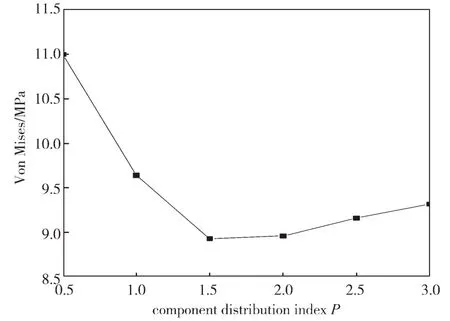
图6 成分分布指数对残余热应力的影响Fig.6 Effects of the component distribution index on residual stress

由图6 可知，随着P 值的增大，涂层的残余热应力最大值呈现先减小后增大的变化趋势，其中，P值为1.5 时的残余热应力最大值（8.93 MPa）最小，其相较于P 值为0.5 时的残余应力最大值（11 MPa）减小了18.8%。这是由于小的P 值会增大黏结层和梯度层的材料不匹配性，而大的P 值会增大涂层的表层和近表层的材料不匹配性[20]，最终导致涂层中残余热应力增大。

2.4 梯度涂层的结构优化

根据前面的单因素分析结果，拟采用正交试验法确定多层涂层的最优结构参数。以残余热应力最大值为优化目标，其值越小越好，考察梯度层的层数与厚度、成分分布指数3 个因素，表2 为其水平表。选用四因素三水平的L9(34)正交试验表，如表3 所示。

表2 因素水平表Table 2 Orthogonal factor level table

对正交试验分析结果进行极差分析，可得各因素对涂层残余热应力的影响程度，又能确定因素水平的最优组合。表3 为正交分析和极差分析结果，由表3 可知，序号9 的残余热应力最大值最小。观察序号9 对应的各因素最小K 值，得到最佳的参数组合为A3B3C2，即梯度层数为7 层，梯度层厚度为1.0 μm，成分分布指数为1.5。另外，表中的极差值R 中，B因素最大，A 因素次之，C 因素最小，即这3 个因素对Nb2O5/Nb2O5-Ti/Ti 多层涂层残余热应力的影响程度由大到小依次为梯度层厚度、层数和成分分布指数。

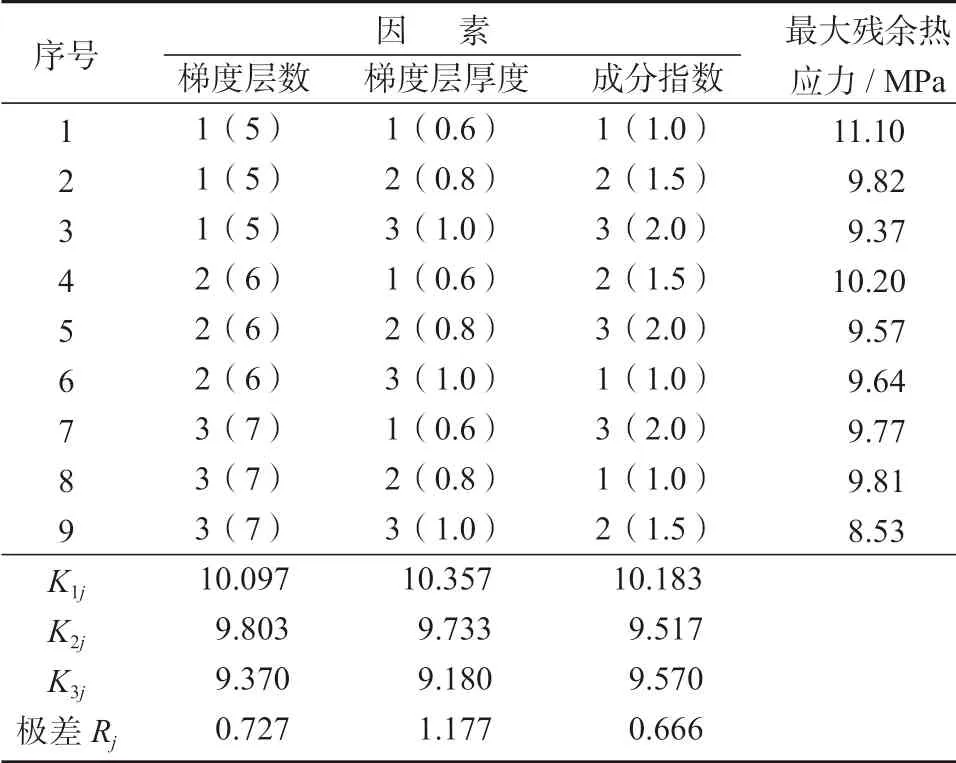
表3 正交分析方案及结果Table 3 Orthogonal analysis scheme with its results

2.5 优化后的多层涂层与单层、双层涂层的残余热应力比较

设ZK60 镁合金表面Nb2O5单层、Nb2O5/Ti 双层和Nb2O5/Nb2O5-Ti/Ti 多层涂层（以下分别简称单层、双层和多层涂层）的总厚度相同，均为10.5 μm（如表4 所示），梯度层的层数为7、厚度为1 μm、成分分布指数为1.5，对各涂层进行残余热应力分析，得到如图7 所示的等效残余热应力云图。

表4 涂层厚度Table 4 Coating thickness μm

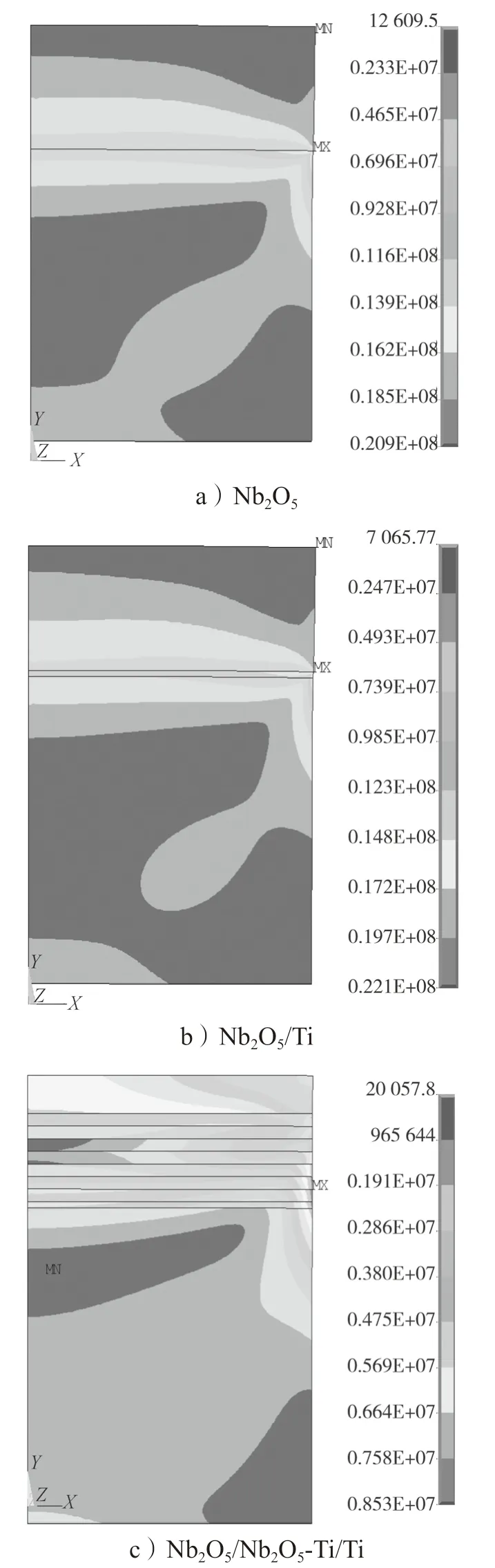
图7 涂层等效残余热应力云图Fig.7 Residual thermal stress nephogram of the coating

由图7 可以得知，多层涂层的最大残余热应力为8.53 MPa，较单层涂层（20.9 MPa）和双层涂层（22.1 MPa）的分别减小了59.2%和61.4%。另外，单层涂层和双层涂层的最大残余热应力分别出现在基体/涂层界面外边缘和黏结层/梯度层界面外边缘处，而多层涂层的最大残余热应力出现在Nb2O5-Ti 梯度层结合界面的外边缘处。由于涂层中的残余应力越大，涂层的结合强度越低，因此梯度结构提高了Nb2O5涂层与基底Ti6Al4V 之间的结合性能，增强了涂层对基体的保护作用。

3 结论

本研究采用有限元方法分析了Ti6Al4V 表面Nb2O5/Nb2O5-Ti/Ti 多层涂层残余热应力的分布特征，研究了中间梯度层Nb2O5-Ti 的层数与厚度、成分分布指数等对多层涂层残余热应力的影响，可得到如下结论：

1）当梯度层层数由1 层增加到6 层时，多层涂层的残余应力最大值由12.6 MPa 减小到11.7 MPa，降幅为7.1%，但是当层数继续增加到8 层时，涂层的残余热应力最大值无明显变化。

2）随着梯度层厚度的增大，涂层的残余热应力最大值下降速率降低。其中，涂层厚度由0.2 μm 增加1.0 μm 时，最大残余热应力由13 MPa 减小到9.4 MPa，下降速率为4.5 MPa/μm；而厚度由1.0 μm 增大到2.0 μm时，最大残余热应力由9.4 MPa减小到7.26 MPa，下降速率为2.14 MPa/μm。

3）随着P 值的增大，残余热应力最大值呈现先减小后增大的变化趋势，其中P 值为1.5 时的残余热应力最大值（8.93 MPa）最小。

4）通过正交试验法，得到了中间梯度层的最优结构参数组合，即梯度层层数为7，梯度层厚度为1 μm，成分分布指数为1.5。该涂层的最大残余热应力为8.53 MPa，较单层涂层（20.9 MPa）和双层涂层（22.1 MPa）分别减小了59.2%和61.4%。