可轧制约束下VRB 薄壁结构的厚度分布优化方法研究*

陈有松，沈国民，段利斌

(1. 上汽集团商用车技术中心，上海 200483；2. 江苏大学汽车与交通工程学院，镇江 212013)

前言

薄壁结构具备优秀的耐撞性能与轻量化潜力，广泛应用于汽车车身结构设计。在实际汽车设计问题中，门槛、前防撞梁和B 柱[1]等通常承受横向冲击载荷，变形呈现为弯曲塌陷模式。研究薄壁梁结构的抗弯性能对车身结构耐撞性和轻量化设计具有重要指导意义。在弯曲塌陷模式中，通常大的塑性变形集中在塑料铰链附近，而结构的其余部分变形很小，造成薄壁梁弱承载区域材料浪费，而塑性铰区域材料不足[2]。为提高结构的耐撞性与轻量化性能，连续变厚度轧制工艺(variable－thickness rolled blanks，VRB)得以广泛应用于车身结构中，它通过柔性轧制技术调整轧辊之间的距离，使板材厚度可沿轧制方向变化[3]。设计人员根据承载工况合理分布结构的厚度，实现基于性能定制和功能定制设计，使材料利用率最大化，从而实现轻量化设计。

VRB 薄壁梁的厚度分布设计问题一直是研究热点。孙光永等[4]提出了功能梯度厚度管(functionally graded thickness，FGT)，即薄壁管的厚度服从幂指数分布形式，研究结果表明，FGT 管的耐撞性能和轻量化潜力远远优于传统等厚度管。Zhang等[5－6]研究了横截面变厚度薄壁方管的弯曲塌陷模式，并对横截面厚度分布进行了优化设计，有效改善了其抗弯曲性能。段利斌等[7－8]提出一种多段式变厚度帽型梁(tailor－rolled blank thin－walled structure，TRB－TH)，分别在三点弯曲载荷下和轴向压溃载荷下对其进行耐撞性和轻量化优化设计。童泽奇等[9]结合VRB 轧制工艺约束，利用混合元胞自动机方法对受横向冲击的VRB 帽型梁进行了厚度分布设计。尽管目前VRB 薄壁梁的结构设计研究取得了很多成果，但这些成果均预先定义了VRB 薄壁梁的厚度分布形式，进而建立代理模型开展优化设计。这一方面限定了VRB 结构的厚度分布形式，限制了VRB 薄壁梁的轻量化潜力；另一方面，当设计变量数量过多时，大多数代理模型拟合这类动态非线性响应的精度会大幅度降低，优化结果的精度无法得到保证。

以帽型梁横向冲击过程为研究对象，基于传统全局优化算法粒子群算法(particle swarm optimizer，PSO)思想，考虑多参数与性能约束优化设计问题，提出一种求解制造约束下VRB 薄壁梁结构最优厚度的综合学习粒子群算法(comprehensive learning particle swarm optimizer，CLPSO)，该算法可以求解制造约束与性能约束下包含大规模设计变量的VRB薄壁梁结构的理想厚度分布问题。

1 VRB 薄壁结构的有限元建模与评价指标

1.1 VRB 单帽型薄壁结构的有限元建模与验证

本文中研究的单帽型薄壁结构包括两种类型，一类为等厚度单帽型薄壁结构，壁厚为1.6 mm；另一类为VRB 单帽型薄壁结构，包括2 个等厚度区域(constant thickness zone，CTZ)和 1 个厚度过渡区(thickness transitions zone，TTZ)，其中 2 个 CTZ的厚度分别为1.2 和2.0 mm，TTZ 的长度为 80 mm，位于2 个 CTZ 的中间位置。样件材料为 HSLA340，长度为400 mm，焊点间距为30 mm，翼缘宽度为105 mm，腹板高度为85 mm，翻边宽度为35.7 mm，如图1 所示。为了保证测试样品的可重复性，每种样品在相同的负载条件下重复3 次试验。

在MTS647 材料试验机上进行准静态三点弯试验，试验装置如图2 所示，样件放在两个圆柱支撑上，支架直径25 mm，跨度L0为300 mm，将直径为25 mm 的圆柱形冲头以5 mm/min 的恒定速度压在样品中部，为保证薄壁梁完全压溃，压头压溃距离设为60 mm。

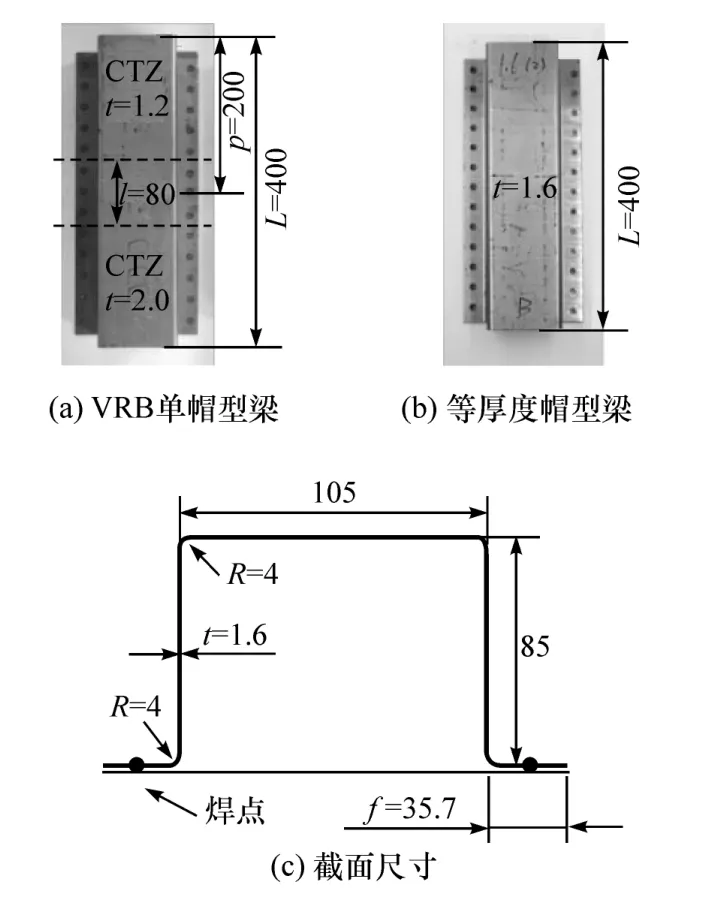
图1 单帽型薄壁梁尺寸(单位:mm)

图2 单帽型薄壁梁试验工况(单位:mm)

利用LS－DYNA 软件建立单帽型薄壁梁的三点弯曲有限元模型。单帽型薄壁结构选用MAT24 号材料；压头和支撑圆柱视为刚性，采用MAT20 号材料，网格大小4 mm。根据实际工况，两个支撑圆柱约束6 个自由度。薄壁梁与压头和支撑圆柱之间的接触采用面面接触(surface－to－suface)，薄壁梁的接触定义为自接触(single surface)，静摩擦因数为0.2，动摩擦因数为0.15。

从VRB 的柔性轧制过程来看，零件的不同厚度位置具有不同的材料特性。因此，在有限元模型中须考虑不同局部区域的变厚度和变材料力学性能。然而，现有的商业软件很难同时构建变厚度和变材料性能的有限元模型。为此，本文中编写了相应的Matlab 程序，用于模拟VRB 单帽型薄壁结构的连续变厚度与变材料性能的特性，具体步骤如下。

步骤1:根据图1 中描述的横截面形状和尺寸，建立厚度均匀的薄壁结构有限元模型。

步骤2:使用Matlab 代码从步骤1 中建立的有限元模型数据文件中读取节点和单元信息。

步骤3:为了真实地模拟厚度变化，将不同的厚度分配给壳单元的4 个节点中的每个节点。如图3(a)所示，通过使用LS－DYNA[10]中的关键字* ELMENT＿SHELL＿THICKNESS 建立具有可变厚度的壳单元，其中n1～n4分别代表节点1 ～节点4；thick.1 ～ thick.4 分 别 代 表 节 点 1 ～ 节 点 4 的 壳厚度。

步骤4:为模拟VRB 结构的可变材料特性，不同厚度单元具有不同的材料性能，其中不同厚度下的材料性能根据段利斌等建立的有效应力与有效塑性应变场中获得[11]，如图3(b)所示。在理想的有限元模型中，应将TTZ 划分为无数段，每一段的最小长度也决定了有限元模型的单元大小，分段的数量根据建模精度的要求确定。

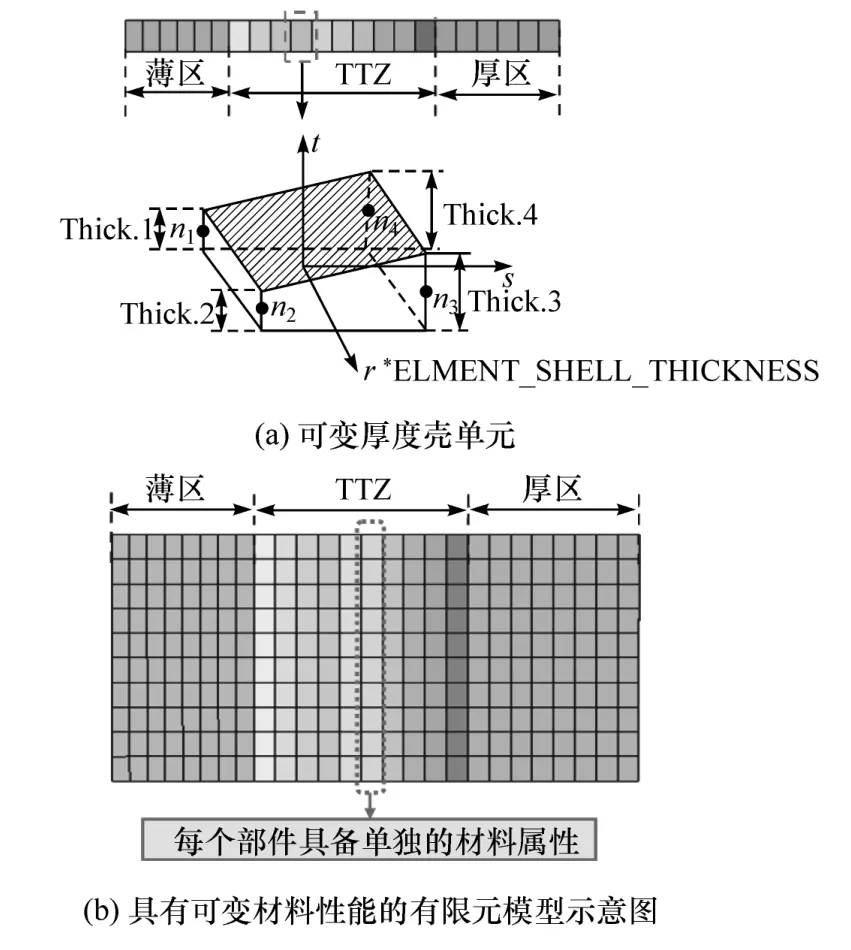
图3 VRB 单帽型薄壁结构的变厚度与变材料性能模拟方法

步骤5:导出具有可变厚度和材料性能的VRB薄壁结构有限元模型。

VRB 单帽型梁和等厚度帽型梁的试验与仿真结果对比如表1 所示，图4 所示为弯矩－转角曲线与能量－转角曲线。由表1 和图4 可知，数值仿真结果与试验结果非常吻合。

表1 试验与有限元模型仿真的吸能结果对比

VRB 单帽型薄壁结构与等厚度薄壁结构的永久变形模式分别如图5(a)和图5(b)所示，试验样品之间的差异小，试验样品总体上具有良好的可重复性。数值模拟预测的最终变形模式与试验相似。综上所述，本文中建立的有限元仿真模型可以较真实地还原试验过程，具有较高的模拟精度，可以在后续研究中代替物理试验过程。

1.2 VRB 薄壁结构抗弯特性的评价指标

图4 试验与仿真的弯矩－转角曲线和能量－转角曲线

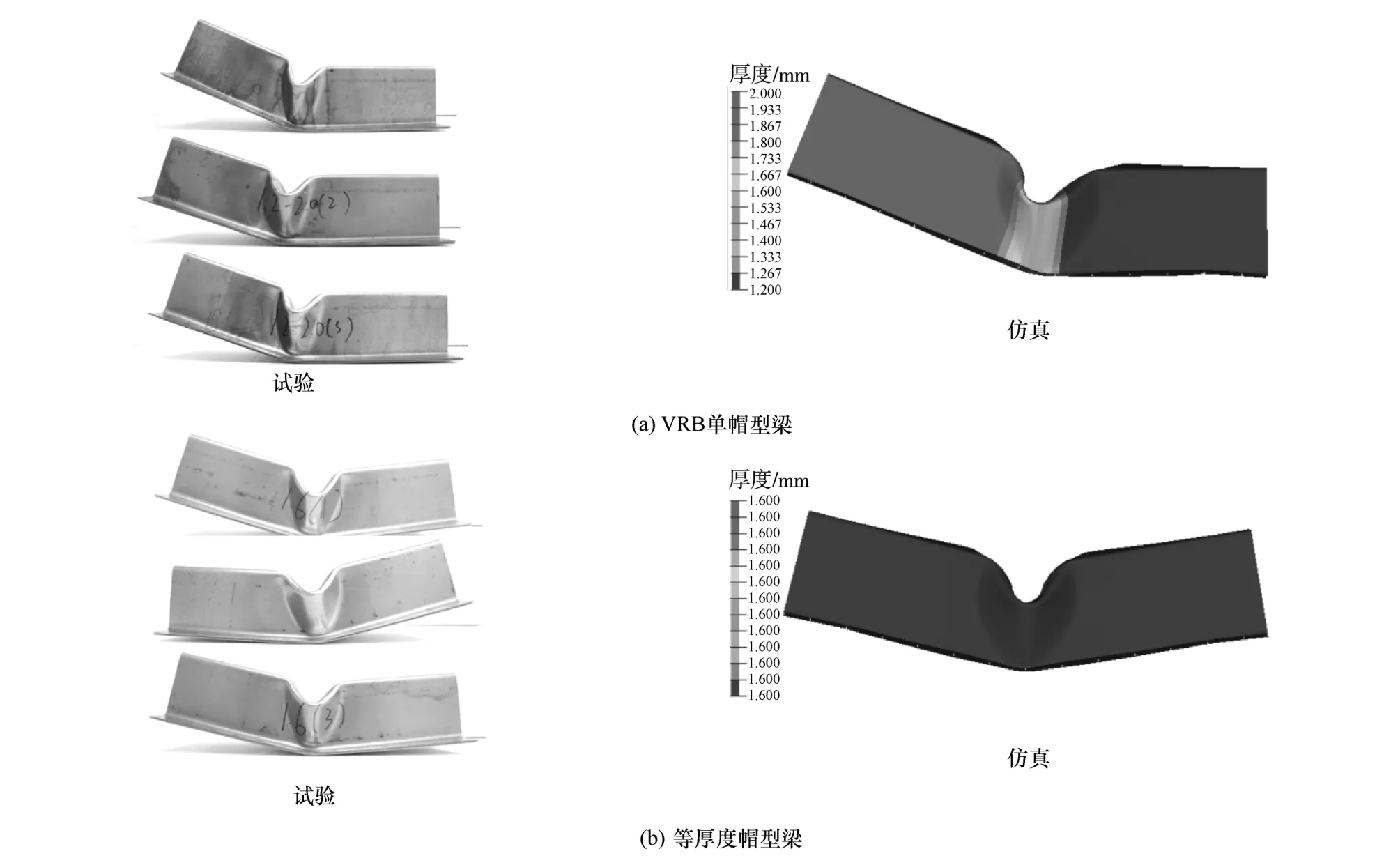
图5 试验与仿真的变形模式对比

乘用车B 柱通常在整车侧面碰撞中承受动态三点弯曲载荷，通常以B 柱的侵入量 、侵入速度以及侵入形态等指标评价整车碰撞安全性能[12]。针对汽车B 柱的应用环境，评价指标如下:

(1) 最大侵入量d在侧面碰撞过程，B 柱的侵入量是乘员损伤的重要影响因素，较小的侵入量能很好的保证乘员舱空间，减小乘员损伤；

(2) 最大侵入速度v若碰撞侵入速度过高，会对乘员重要器官造成严重伤害，因此，最大侵入速度也是薄壁梁抗弯性能的重要评价指标。

2 综合学习粒子群算法

2.1 传统粒子群算法(PSO)

受鸟群觅食行为的启发，Eberhart 和Kennedy 提出了粒子群优化算法(PSO)[13]。PSO 算法将个体解看作单个粒子，在D维搜索空间内以一定速度飞行，寻找取得适应度值最小的粒子位置；粒子的速度根据自身历史最优位置和群体的最优位置进行调整。设第i个粒子的状态为第i个粒子的速度为粒子根据式(1)和式(2)进行迭代更新。

式中:w为惯性权重；C1和C2为学习因子；r1和r2均为[0，1]之间的随机数为第i个粒子的自身历史最优位置为群体最优位置。

2.2 综合学习粒子群算法(CLPSO)

尽管PSO 具有很强的全局搜索能力，但是传统PSO 算法在解决超高维的VRB 薄壁结构厚度优化问题时极易出现早熟[14]。为了解决上述问题，本文中利用综合学习粒子群算法(comprehensive learning particle swarm optimizer，CLPSO)[15]开展可轧制约束下VRB 薄壁结构最优厚度分布的优化设计，算法步骤如下。

步骤1:设置种群规模P，最大迭代次数kmax，初始迭代次数k＝0，种群中随机生成粒子。

步骤2:计算粒子的适应度函数值，个体最优位置和全局最优位置。

步骤3:定义粒子刷新间隙m，第i个粒子的适应度改善状态flagi，初始迭代flagi＝0；比较flagi与m的大小，若flagi≥m时，进入步骤 4；若flagi＜m，进入步骤5。

步骤4:将flagi置0，然后根据PSO 算法中的式(1)和式(2)更新粒子速度与粒子位置。

步骤5:若粒子适应度值未改善，即F(xi)≤F(pbesti)，flagi增加 1，否则将flagi置 0；然后，根据式(3)和式(4)更新粒子每个维度的速度和位置。

式中fi＝[fi(1) ，fi(2)，…fi(d)，…，fi(D)]为粒子当前维度的学习方向，fi(d)更新方式如下:

步骤5.1 从粒子的首个维度开始，每个维度生成一个随机数，若该随机数小于学习概率Pc，进入步骤5.1，否则，相应维度将向自身历史最优位置学习，即fi(d)＝i；

步骤5.2 从种群中随机选择两个粒子比较适应度值，粒子的当前维度向适应度值更小的粒子学习，如图 6 所示，图中，p为粒子总数量，rand，rand1i(d)，rand2i(d)均为[0，1]之间的随机数，F为粒子的适应度值，D为粒子的总维度，d为粒子的当前维度，学习概率Pc更新方式如式(5)所示。

图6 粒子每个维度学习方向fi 的更新策略

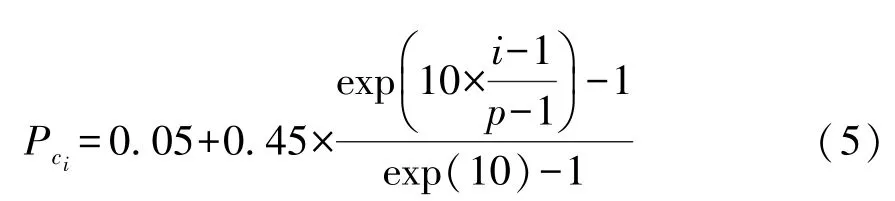
步骤6:判断种群内所有粒子位置是否更新完成，若i＜P，返回步骤2，否则进入步骤7。

步骤7:判断是否达到算法停止条件，若k＜kmax，返回步骤2，否则，输出结果，算法结束。

CLPSO 算法的控制策略如图7 所示。在粒子迭代寻优过程中，当满足flagi＜m时，粒子的不同维度将随机向自身或者其它粒子学习。这种寻优方式扩大了粒子的全局搜索能力，保证了粒子高维空间中群体的多样性，以避免在高维度问题优化中出现早熟。同时，刷新间隙m也很大程度上避免了粒子在不良方向上过多的浪费时间。

图7 CLPSO 算法控制策略

3 基于CLPSO 算法的VRB 薄壁结构的厚度分布优化设计

3.1 优化问题定义

假设VRB 单帽型薄壁结构受到半径12.5 mm圆柱的动态冲击载荷，圆柱质量80 kg，冲击速度5 m/s，如图 8 所示。为了充分挖掘 VRB 薄壁薄壁结构的轻量化潜力，将单帽型梁沿轧制方向划分为100 个部件，每个部件的厚度xd作为设计变量，设计变量矩阵为X＝[x1，x2，… ，x100]。初始的等厚度单帽型薄壁梁的厚度为1.6 mm，质量为2.58 kg，最大侵入量79.3 mm，最大侵入速度7.54 m/s。

以VRB 单帽型薄壁结构的质量最小为目标函数，以侵入量和侵入速度作为约束函数，设计变量X满足可轧制约束条件，相应的优化方程为

式中:M(X)为帽型梁的质量；d和v分别为当前粒子的最大侵入量与最大侵入速度；d0和v0分别为侵入量约束与侵入速度的约束边界；Xmin和Xmax为满足可轧制约束条件下的厚度上下限。

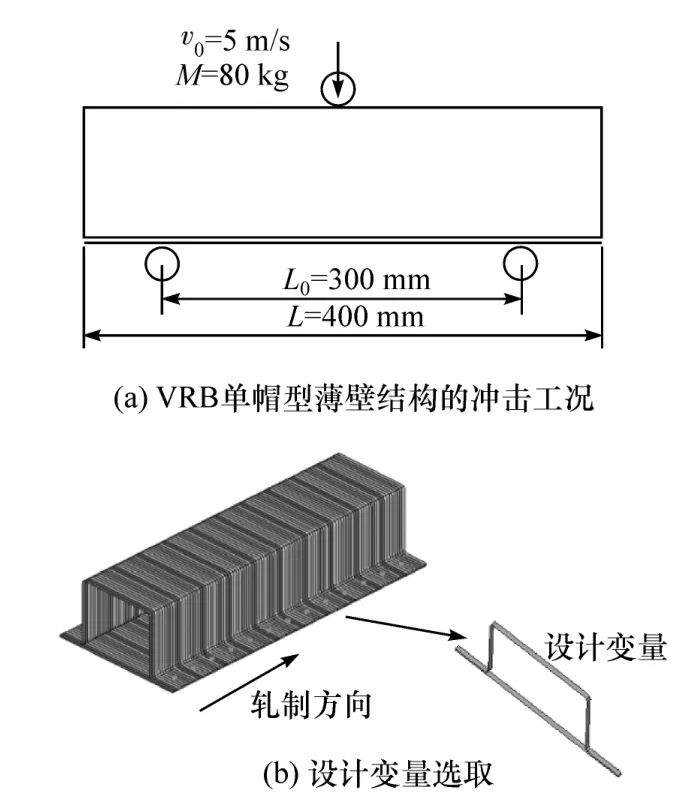
图8 VRB 单帽型薄壁结构的设计变量定义

3.2 适应度函数的定义

对于有性能约束的VRB 单帽型薄壁结构的优化问题，满足约束条件的解称为可行解，反之则为不可行解。本文中采用罚函数法处理性能约束，此时适应度函数的数学表达式为

式中:ed为当前粒子的罚值；K为罚值系数；Ked通常设置为一个远大于粒子总质量M(X)的值。

当粒子为可行解时，ed＝0，粒子适应度值F(X)等于粒子总质量M(X)；当粒子为不可行解时，ed大于0，Ked取值很大，粒子适应度值远大于粒子质量。该方法保证了满足约束的个体的适应度值始终小于不满足约束的个体，且约束不满足程度越小，适应度值越小。

3.3 VRB 薄壁结构的可轧制约束条件转化

根据连续变厚度轧制工艺的制造要求，VRB 单帽型薄壁结构的厚度分布应满足以下约束条件[15]:(1)同一VRB 板材的最大厚度下压量应小于等于50%，换句话说，VRB 薄壁结构的最大厚度与最小厚度的比值应小于等于2∶1；(2)过渡区的斜率必须在1∶100 之内。

考虑到VRB 轧制工艺，在CLPSO 算法更新粒子位置后增加VRB 工艺约束条件，以使更新的粒子位置满足可轧制约束，带 VRB 工艺约束问题的CLPSO 算法流程如图9 所示。

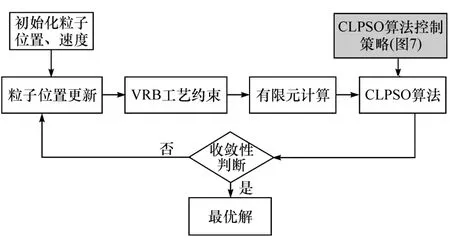
图9 带VRB 工艺约束问题的CLPSO 算法

VRB 工艺约束如下，为满足厚度下压量约束条件，对设计变量X进行更新[16]:

根据VRB 板材厚度过渡区的斜率要求，设VRB薄壁结构的单个设计变量沿轧制方向的长度为h，则相邻两个元胞间的厚度差应小于等于0.01h；更新单个设计变量的厚度该设计变量位置为L；从第L个设计变量开始，根据式(11)和式(12)依次更新其相邻设计变量的厚度。

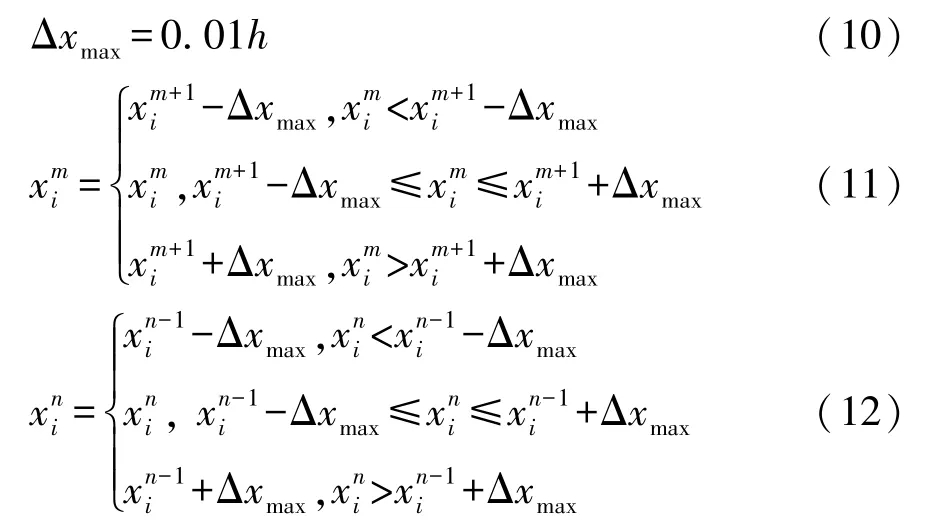
式中:Δxmax为相邻设计变量间厚度差的最大值，即相邻设计变量间厚度差应不大于分别为第i个粒子中第m、n个设计变量的厚度值，其中m∈[1，L－1]，n∈[L＋1，N]，N为设计变量总数。为了便于阐述，第L、m、n个设计变量在VRB 薄壁结构中的位置如图10 所示。

图10 VRB 单帽型梁的设计变量位置示意图

3.4 优化结果分析

本文中利用CLPSO 算法开展了考虑VRB 轧制约束与不考虑VRB 轧制约束的单帽型薄壁结构的厚度分布优化设计。这两个优化问题的侵入量约束边界d0＝75 mm，侵入速度约束边界v0＝7.3 m/s。

算例I、算例Ⅱ迭代过程如图11 和图12 所示，在迭代过程中满足性能约束的条件下，质量平稳下降，收敛性较好。最优解与初始等厚度帽型梁的质量、侵入量、侵入速度对比如表2 所示。可以看到，在满足侵入量与侵入速度约束的条件下，算例I 与算例Ⅱ最优解质量相对于等厚度帽型梁分别下降了25.3%和21.7%。

图11 不考虑VRB 工艺约束算例的迭代过程

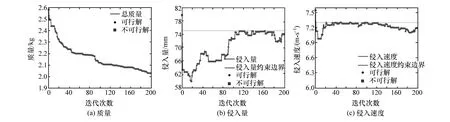
图12 考虑VRB 工艺约束算例的迭代过程

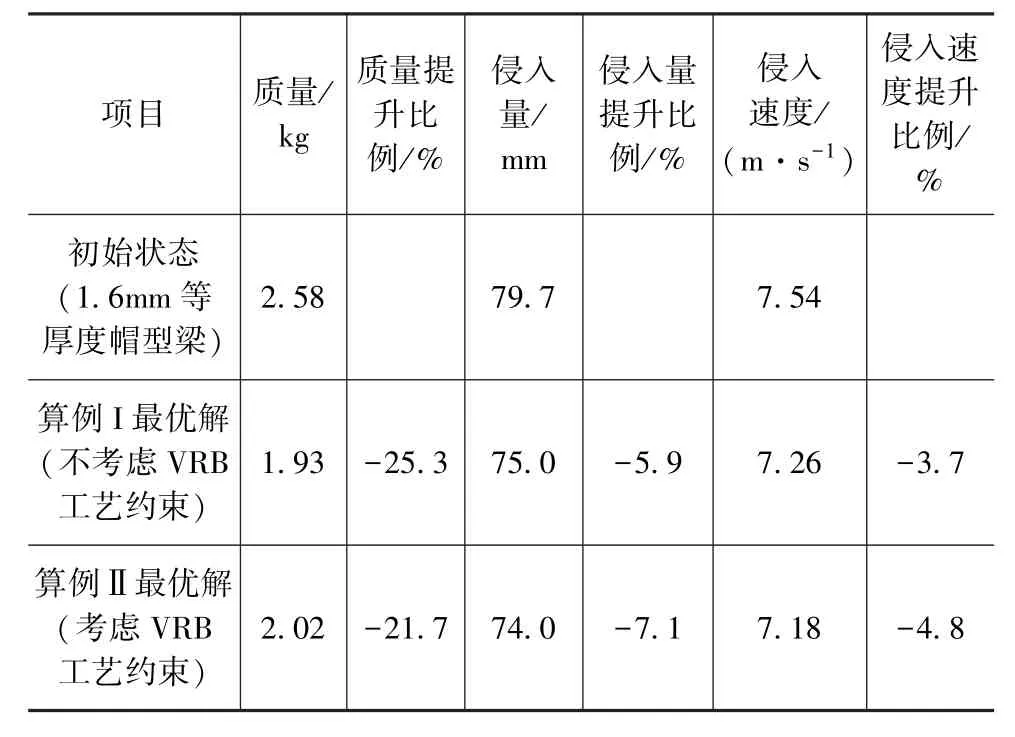
表2 最优解与等厚度帽型梁的质量、侵入量和侵入速度对比

最优解厚度分布对比如图13 所示，算例I 的VRB 单帽型梁相邻区域厚度过渡不平滑，多个区域厚度分布上下振荡，虽然轻量化性能优于算例Ⅱ，但不满足可轧制工艺要求；算例Ⅱ最优解的厚度分布平滑，满足可轧制工艺要求。

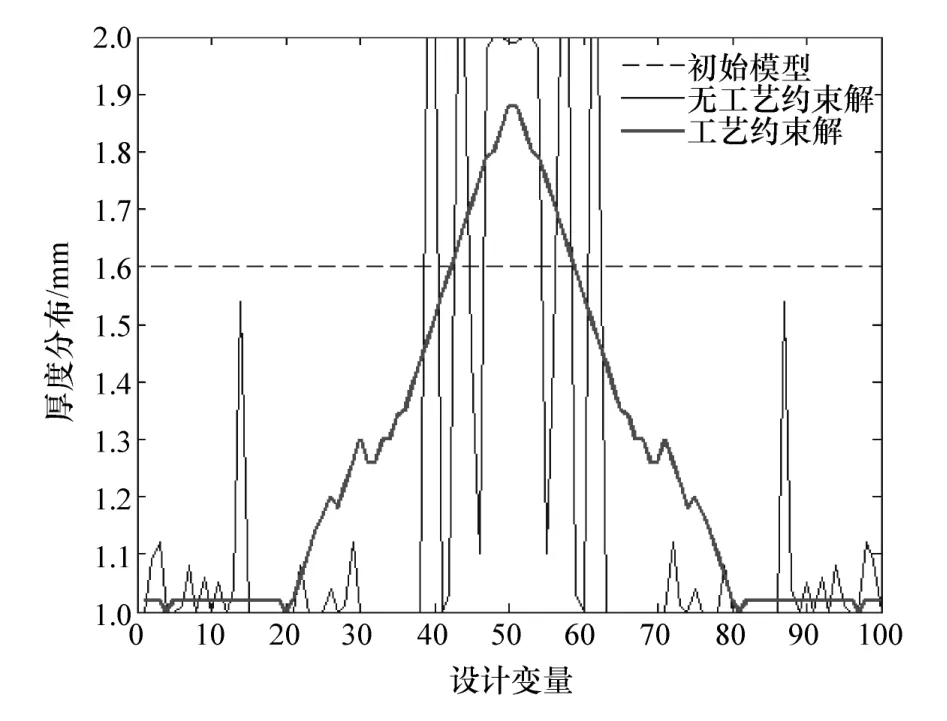
图13 最优解厚度分布

最优解与初始解的应力分布和变形模式如图14 所示，与等厚度帽型梁相比，VRB 单帽型梁应力分布更加均匀。算例I 的应力分布与算例Ⅱ基本一致，均充分利用了材料进行吸能。考虑VRB 工艺约束后，质量仅比不考虑VRB 工艺约束的最优解大4.7%，相对于等厚度帽型梁质量减少21.7%。

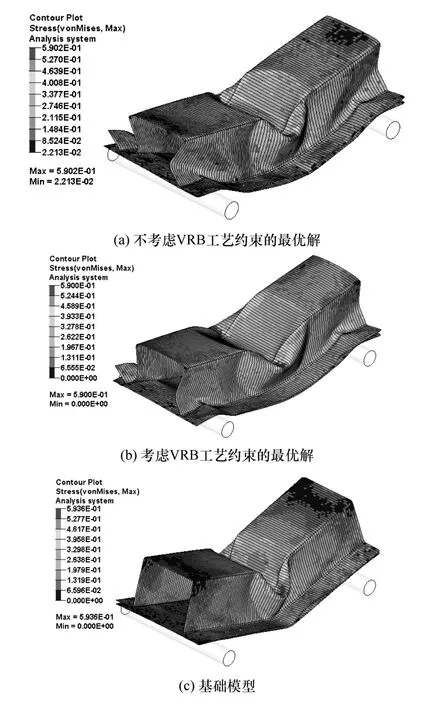
图14 应力云图与变形模式对比

4 结论

(1)提出了考虑性能约束与VRB 轧制工艺约束的CLPSO 算法，优化问题选取了大量设计变量，针对轧制工艺的特点对三点弯曲工况下的帽型梁厚度分布进行合理调控，从而充分释放VRB 单帽型梁的轻量化潜力。

(2)基于CLPSO 对VRB 单帽型梁的厚度分布进行优化设计，结果显示，在满足侵入量与侵入速度约束的条件下，考虑VRB 轧制约束的最优解质量略高于不考虑VRB 轧制约束的最优解，仍具有优秀的轻量化与抗弯性能，为VRB 结构在车身上的应用提供了一定的指导作用。