基于接地特性的轮胎滚阻与抓地性能评价方法*
2021-01-13王国林喻康颖
梁 晨,王国林,喻康颖,梅 烨
(江苏大学汽车与交通工程学院,镇江 212013)
前言
轮胎是影响汽车行驶安全和燃油消耗的关键因素。近年来,欧盟等各国出台的标签法均对轮胎滚动阻力、抓地等性能提出了更高要求,预示着开发绿色高性能轮胎是未来轮胎发展的趋势。
轮胎的接地特性是轮胎结构设计与胶料配方共同作用的结果,反映了轮胎综合性能,可以用接地特征参数从几何和力学两方面来对其进行描述。关于轮胎接地特性的研究主要通过试验测试和数值仿真两种方法展开。获取轮胎接地压力分布和接地印痕的试验方法大致可分为压力板法[1-2]、电测法[3-4]和光测法[5]3 类。Koehne 等[6]通过试验研究了胎面花纹对轮胎接地形态的影响,发现花纹形状对接地几何参数影响较小,但对轮胎的接地力学参数有较大影响。Tomaraee 等[7]通过对轮胎接地印痕图像进行处理获得接地区的几何参数,并通过试验研究了不同载荷和充气压力下接地区长度、宽度和轮胎滚动阻力的定量关系。Juan[8]设计了轮胎接地压力非接触式测量台架,通过试验研究了不同载荷、充气压力、侧偏角对接地压力分布的影响。Radulescu等[9-10]提出接地形状因子来描述轮胎接地印痕的几何形状,并通过试验研究不同带束层结构设计下的轮胎接地形态,发现降低接地形状因子有利于改善轮胎的磨损性能。梁晨[11]提出采用10 个接地几何参数和5 个接地压力参数来描述轮胎接地形态的几何和力学特征。王国林等[12]采用Tekscan 压力测试系统进行轮胎接地压力分布试验,利用主成分分析方法研究各分区接地性态参数与噪声、滚动阻力之间的定性、定量关系。傅相诚等[13]采用有限元方法研究了带束层角度、冠带层结构和胎冠弧设计对轮胎接地印痕形状的影响,通过胎冠弧设计优化了接地印痕进而降低轮胎滚动阻力。
目前国内外学者通过试验或数值仿真方法研究了接地参数变化对轮胎性能的影响。然而已有研究仅局限于接地形态对轮胎单一性能的影响,缺少综合考虑接地特征对轮胎多性能的影响。此外,已有研究采用接地压力参数来描述接地区力学信息,仅能反映接触面法向的力学特征,无法完整表达接地区力学信息。研究表明胎面花纹的变形对轮胎滚阻、抓地性能均有重要影响[14-16]。因此,本文中提出了一种获取轮胎接地区变形分布的试验方法,通过获取试验轮胎接地区的三维变形分布并提取相关变形参数,构建了表达接地区几何和力学信息的参数化评价体系,采用偏最小二乘回归方法提出了一种基于接地参数的轮胎滚动阻力和抓地性能的评价方法。
1 轮胎接地性态试验
1.1 试验轮胎及其性能测试
图1 所示为10 条不同胎面花纹的205/55R16型PCR 试验轮胎,文献[17]中通过试验研究公布了10 条轮胎的滚阻与抓地相关性能数据,见表1。轮胎性能指标测试严格按照欧盟制定的轮胎标签法规执行,其中滚动阻力系数是试验轮胎在滚动速度为80 km/h 时由室内转鼓试验台测得的滚动阻力系数值与参考样胎所测值的比值;制动距离是装载试验轮胎的车辆在指定的干试验路面上以100 km/h 的制动初速度紧急制动至车辆停止时所测的距离。

图1 205/55R16 轮胎花纹

表1 测试轮胎及其性能测试数据
1.2 接地压力分布试验
采用Tekscan 压力测量系统获取试验轮胎的接地压力分布以及接地印迹。试验时轮胎的充气压力为额定气压值240 kPa,载荷为额定载荷4 821 N,轮胎加载是在刚度试验台上通过升降加载机构实现的(见图2)。本文中所采用的Tekscan 压力毯的型号为8000D-2,压力分布测量系统压力测量范围为0-175 MPa,测试精度为±5%,系统分辨率为3.048 mm×3.048 mm。
1.3 接地变形分布试验
采用VIC-3D 全场非接触应变测量系统展开接地变形分布测量试验研究,如图3 所示。试验前,清洁轮胎表面,并对轮胎表面进行散斑化处理,便于VIC-3D 系统能更好地识别图像[18]。试验时,试验工况与接地压力测试时一致,选取玻璃板作为试验轮胎接触基底,并通过放置在玻璃板下方的双目相机分别拍摄试验轮胎加载前、后的接地区域胎面图像。后期处理时,以胎面接地区中心为原点、轮胎前进方向为X轴正方向、轮轴方向由轮胎外侧指向内侧为Y轴正方向、垂直指向玻璃板方向为Z轴正方向建立接地区变形分布三维坐标系。

图2 接地压力分布试验

图3 接地变形分布试验
在进行数字图像相关分析时须先确定图像分析区域即剔除花纹沟槽区后的胎面区域。分析区域边界的确定方法如图4 所示,通过图像处理来增加所拍摄图像的对比度,利用胎面和沟槽侧壁边界处的分界来划分分析区域。确定分析区域后,基于数字图像相关技术对分析区域进行图像相关分析和变形量计算即可得到加载后分析区域内像素点的三维坐标、位移和应变。
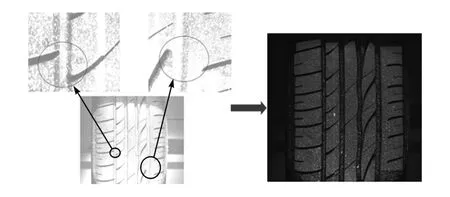
图4 图像分析区域
然而变形分析计算的分析区域中包括了未与玻璃板接触的胎面区域,因此需要进行接地区域的筛选得到实际接地区的变形分布。本文中通过设定图像中像素点的Z坐标阈值(即Z′)来确定接地区域,当Z>Z′即认为所筛选的区域为接地区域。将试验轮胎分析区域像素点加载后的Z坐标值进行降序排列后得到Z坐标分布曲线,选取Z坐标分布曲线上的2 阶微分绝对值最大的点作为Z坐标阈值。图5为1 号试验轮胎在筛选前和筛选后分析区域像素点的Z坐标分布图。接地压力分布试验和接地变形分布试验所得到的接地几何参数对比如表2 所示,表中A 列和B 列分别对应接地压力分布和接地变形分布测量试验所得到的接地几何参数,结果表明接地长度和宽度的误差均在5%以下,说明接地区域筛选方法是有效的。
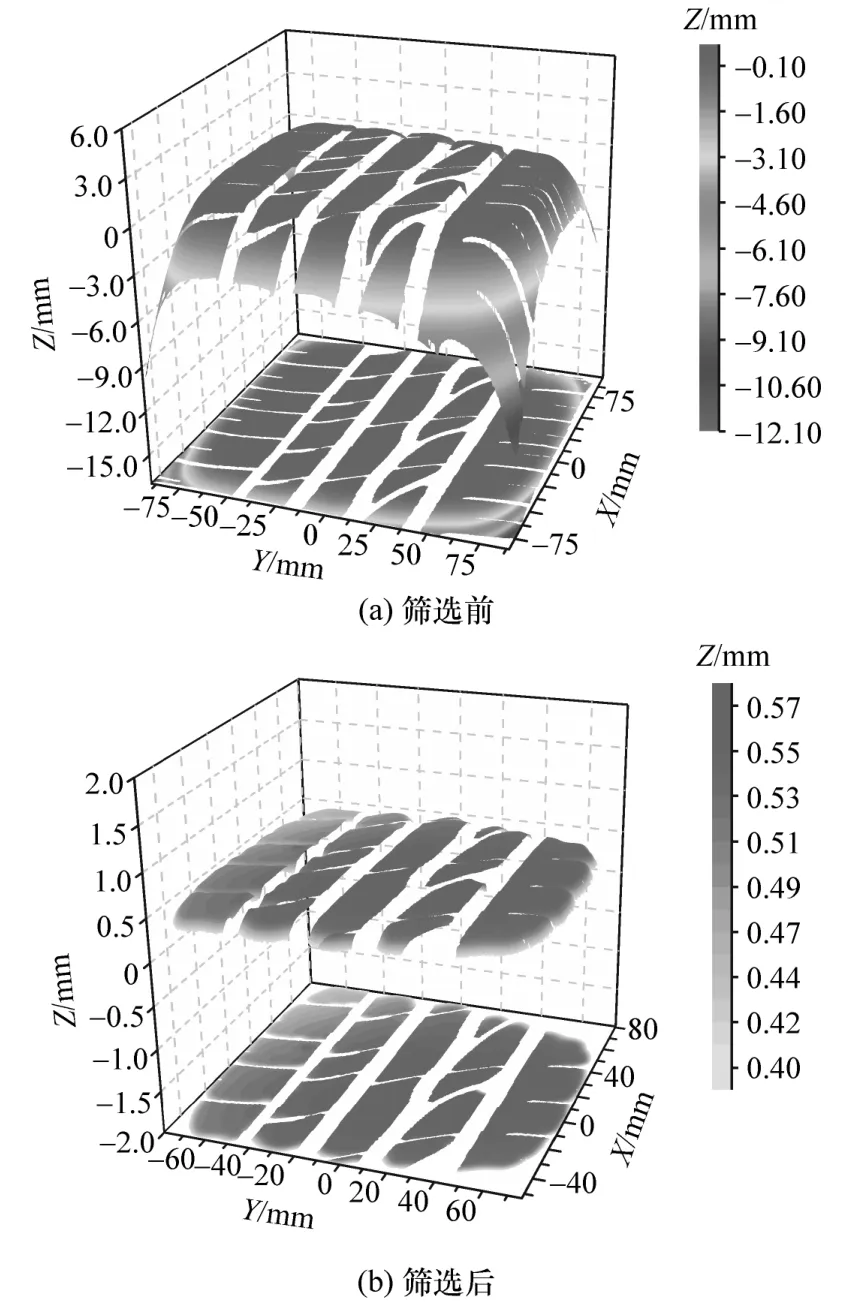
图5 1 号试验轮胎接地区域的筛选

表2 接地几何参数的对比
本文中所使用的VIC-3D 测量系统,只能获取被测物体表面的二维应变分布即接地区胎面的X和Y方向应变,而Z方向的接地区胎面变形可以通过加载后轮辋和接地区胎面相对于玻璃板的Z向位移进行叠加计算来获得,具体的接地区胎面三维变形计算方法如下。
(1)接地区胎面的径向变形的定义为加载后胎面区域相对于轮辋(轮辋假设为刚体)的Z方向变形,记为R,可由式(1)计算。

式中:ΔZ为加载后轮胎的下沉量即轮辋相对于玻璃板在Z方向的位移,可由轮轴升降机构上的位移传感器测量;ΔZ′为加载后胎面区域相对玻璃板的Z方向位移,可由接地区变形分布试验获取。
(2)接地区胎面的X和Y方向应变的计算公式为

式中:(x,y)为接地区胎面像素点的XY平面坐标;u(x,y)和v(x,y)分别为X和Y方向位移形函数,通过对所测得的位移场分布进行插值拟合来获得接地区胎面的位移形函数。
图6 为1 号试验轮胎在加载后接地区胎面的变形分布特征。由图6(a)和图6(b)可见:胎肩区域在XY平面的主应变表现为以纵向拉伸变形为主,胎肩内侧靠近纵沟的胎面区域主要为横向拉伸变形;中间3 个肋条状花纹块区域在XY平面的主应变以横向拉伸变形为主;花纹块变形分布表现为沟槽附近的胎面区域变形较大,靠近花纹块中心区域的变形较小。由图6(c) ~图 6(e)可见:外、内胎肩区域在X方向(纵向)变形主要表现为拉伸变形,Y方向(横向)变形主要表现为压缩变形;中间3 个肋条区域在X方向变形主要表现为压缩变形,Y方向变形主要表现为拉伸变形;接地区径向变形分布呈现出中心区域的径向变形最大,从中心区域过渡到边缘区域时径向变形逐渐减小。图6(f)展示了接地区胎面在XY平面内等效应变(Von-Mises 应变)分布,反映了接地区胎面在XY平面内变形量的大小,可以看出接地区域内胎肩区的等效应变较大。
2 轮胎接地特征参数
轮胎的接地特性可以用接地特征参数从几何和力学两方面来进行描述。文献[11]和文献[12]中详细定义了轮胎接地几何、压力参数,本文中在此基础上定义了描述接地区变形分布的接地变形参数。
2.1 接地区域的划分
考虑到目前乘用车轮胎的胎面多采用非对称花纹设计,因此对胎面进行细化分区。本文中研究对象的胎面均有4 条环形纵沟槽,由轮胎外侧到内侧依次命名为沟槽1-沟槽4,如图7 所示。按纵沟的位置分布将轮胎接地区划分为5 个区域,由外到内依次为外胎肩(Ⅰ)、外过渡(Ⅱ)、中心区(Ⅲ)、内过渡(Ⅳ)和内胎肩(Ⅴ)。本文中在文献[11]和文献[12]定义的接地几何和压力参数上增加了环形纵沟槽的宽度和荷重比两个参数,荷重比为每个分区胎面的承载占总载荷的比例。
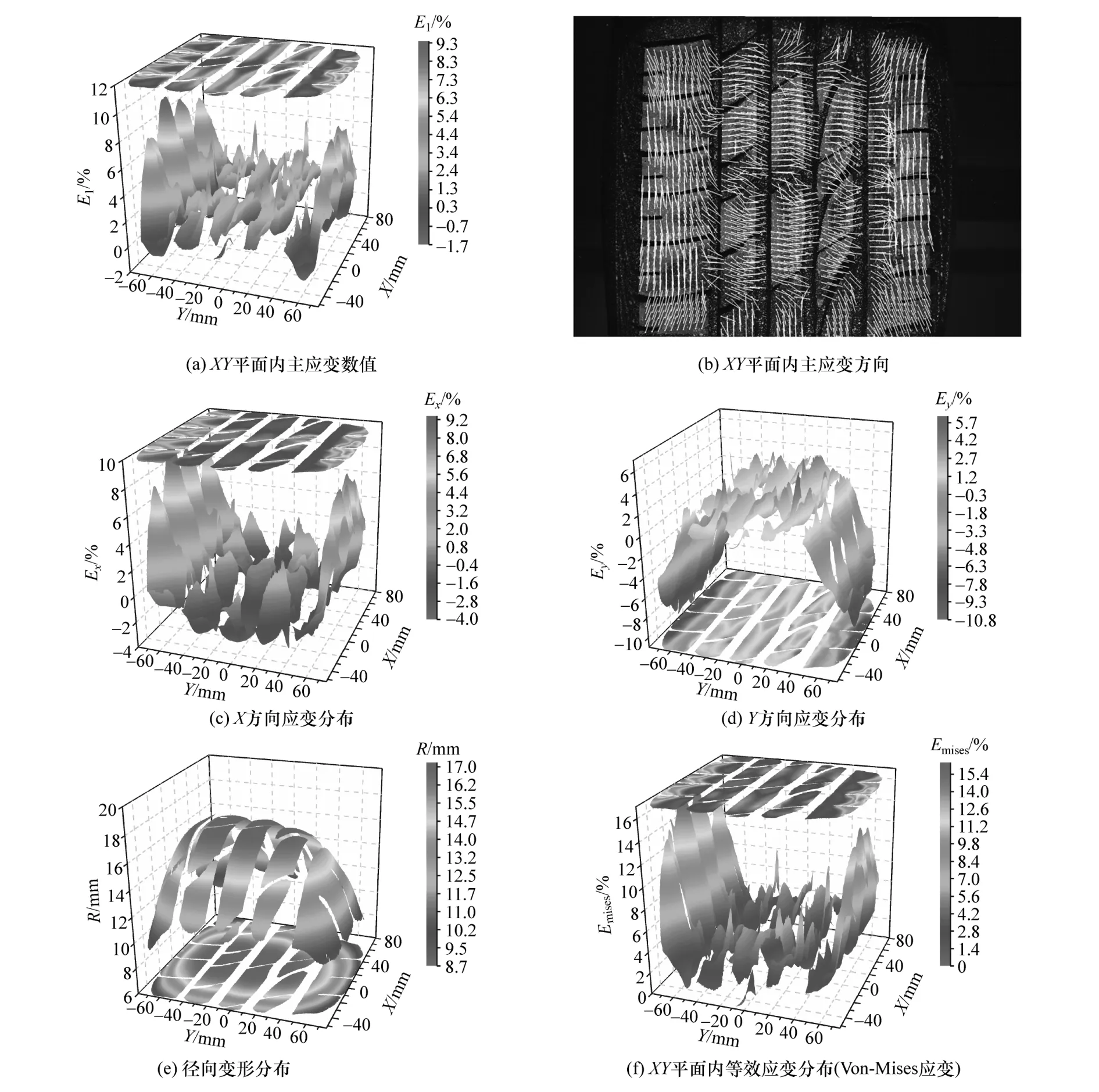
图6 1 号试验轮胎接地区变形分布

图7 接地区域的划分
2.2 接地变形参数
为了定量描述接地区的变形分布特征,本文中在整个接地区域以及5 个分区分别定义了9 个接地变形参数对应整个接地区域,对应外胎肩区域,对应外过渡区域,以此类推),共计 54 个接地变形参数。
3 数据分析
通过对上述接地参数间进行相关分析发现变量间具有明显的共线性,且本研究中由于试验条件的限制导致试验样本数少于自变量数,采用常规的最小二乘回归无法达到理想的回归精度[19],因此采用偏最小二乘回归(PLSR)方法对轮胎性能指标和接地参数进行多元线性回归分析。
3.1 接地参数筛选
为提高分析效率,在进行PLSR 分析前须先剔除影响较低的参数。采用Pearson 相关系数r来度量两个变量线性相关的强弱:

式中:n为样本数;为各轮胎性能测试值及其平均值;为各轮胎接地参数及其平均值。
将6 个区域共计138 个接地特征参数与表1 中的性能测试值进行相关分析,筛选出与轮胎滚阻、抓地性能显著相关(0.5<|r|)的接地参数。表 3 列出了滚动阻力系数与接地参数的相关分析结果,可以看出:降低接地区XY平面内等效应变的大小和分布的不均匀性可以有效降低轮胎滚动阻力系数;在保证轮胎高宽比一定的情况下,增加Ⅰ、Ⅱ区域的胎面弧高度能有效降低轮胎的滚动阻力。表4 列出了制动距离与接地参数的相关分析结果,可以看出:降低接地区胎面Y方向(横向)的拉伸应变同时增加接地区胎面X方向(纵向)的拉伸应变能有效提升轮胎的抓地性能;此外接地区各区域胎面的载荷分配和制动距离显著相关,增加中心区域的承载比例,降低胎肩区域的承载比例能有效提升轮胎的抓地性能。

表3 滚动阻力系数高相关接地参数
3.2 轮胎滚动阻力与抓地性能的矛盾机理
通过上述分析可知接地区胎面变形对轮胎的滚动阻力和抓地性能均有重要影响。表5 列出了不同方向上接地区胎面变形对轮胎滚动阻力和抓地性能的影响,其中“+”和“-”分别表示正相关和负相关。接地区胎面橡胶在受载后径向产生压缩变形时,X和Y方向变形主要表现为拉伸变形。提升轮胎的抓地性能需要降低接地区胎面Y方向的拉伸变形同时增加X方向的拉伸变形,但随着X方向拉伸变形的增加轮胎的滚动阻力也会增加,这导致了滚动阻力和抓地性能的矛盾。
3.3 高相关接地参数的偏最小二乘回归分析
为保证结果的可靠性,须对筛选的接地参数和性能指标数据进行标准化处理,计算公式如下:

式中:xij为参数值;为参数平均值。
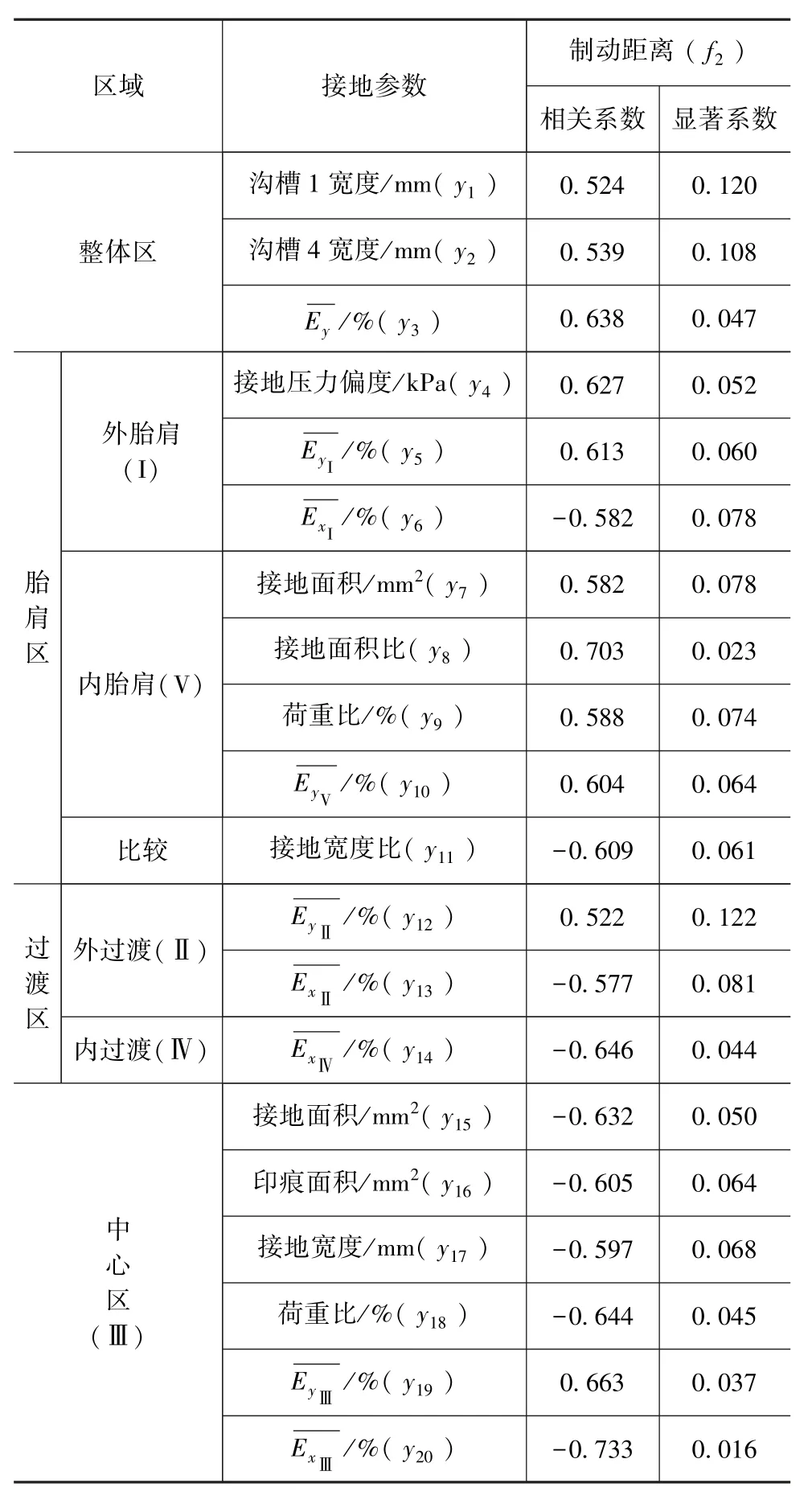
表4 轮胎制动距离高相关接地参数

表5 接地区胎面变形对轮胎性能的影响
根据偏最小二乘回归分析方法的计算原理编写相应的Matlab 程序进行分析。交叉有效性检验得因此最终提取了3 个成分。所提取的3 个成分解释了接地参数82%信息,滚动阻力系数值98%的信息,能包括接地参数和滚动阻力系数值的绝大多数信息。计算得到各成分和指标量(标准化后的数据)之间的关系式为

滚动阻力系数F1和成分间的关系为
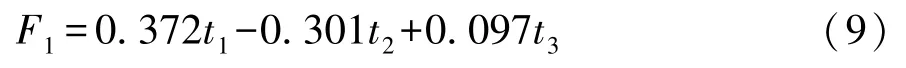
将式(6)~式(8)代入式(9)得到标准化变量的PLSR 模型:
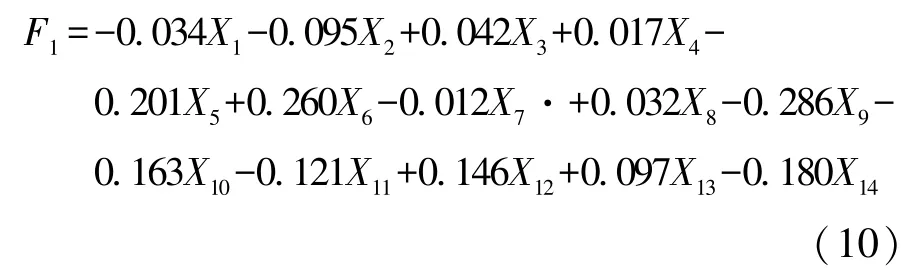
采用Bootstrap 方法(重抽样自助法)对回归系数进行显著性检验,剔除对系统无解释作用的变量,达到简化模型的目的[20]。取Bootstrap 样本1 000个(B=1000),样本容量nB=9。按照检验水平α= 0.1进行参数显著性检验分析得到自变量的临界值,若自变量的临界值小于回归系数的绝对值则认为自变量通过显著性检验。滚动阻力系数PLSR 回归模型中的14 个接地参数标准值的回归系数检验结果如表 6 所示,结果表明自变量X5、X6、X9、X11、X12、X13、X14通过了检验。将经过筛选的变量重新进行PLSR回归分析,所筛选的7 个自变量均能通过显著性检验,得到滚动阻力系数的标准化PLSR 回归模型:
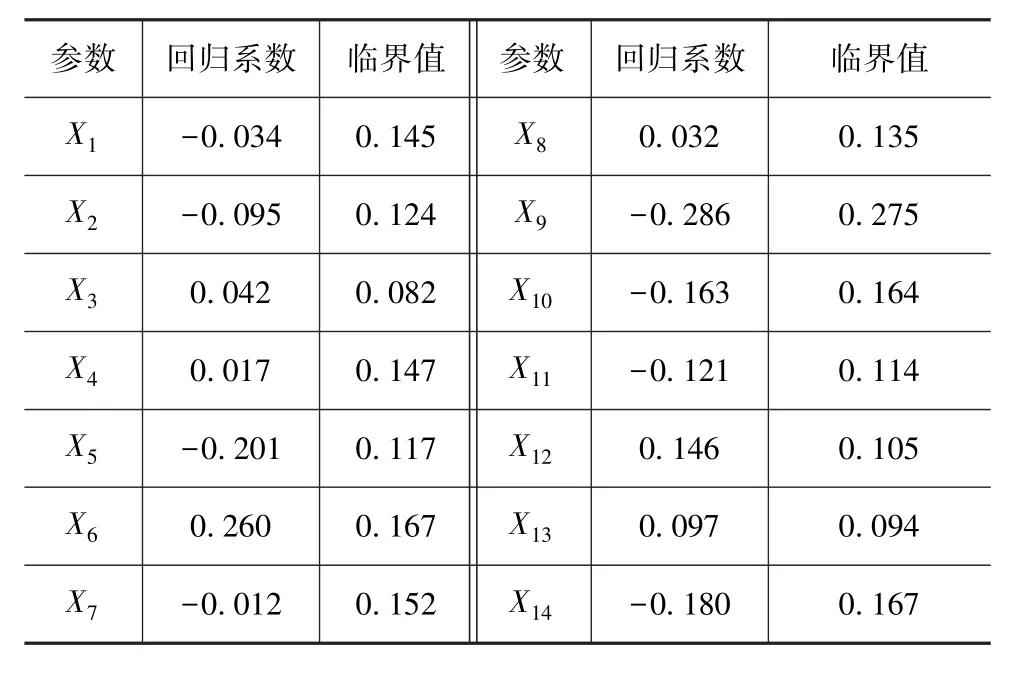
表6 14 个自变量回归系数的Bootstrap 检验
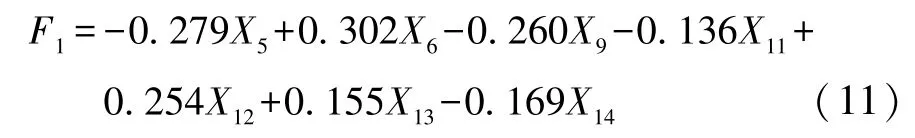
通过比较滚动阻力系数的标准化PLSR 模型回归系数的绝对值大小,对滚动阻力系数影响作用由大到小依次的接地参数为:外胎肩XY平面等效应变(+)、外胎肩胎面平均高度(-)、外过渡区接地长宽比(-)、外过渡区横向拉伸应变的偏度值(+)、外内过渡区平均接地压力比(-)、内过渡区XY平面等效应变(+)、外过渡区胎面平均高度(-)。
利用式(12)对标准化参数进行逆变化:

式中:x和f1为原始参数;X和F1为标准化参数;为原始参数标准差。将标准化变量关系还原为原始变量的关系:
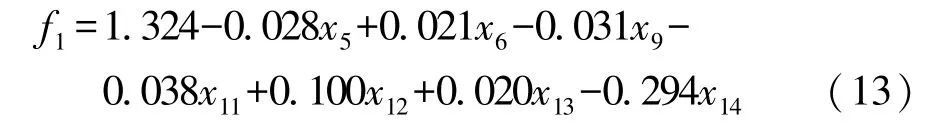
滚动阻力系数的试验值与拟合值对比见表7。由表可见,其最大绝对误差为0.022,最大相对拟合误差为2.367%,回归方程拟合效果较好,可以为同工况同类型轮胎滚动阻力系数提供预测。
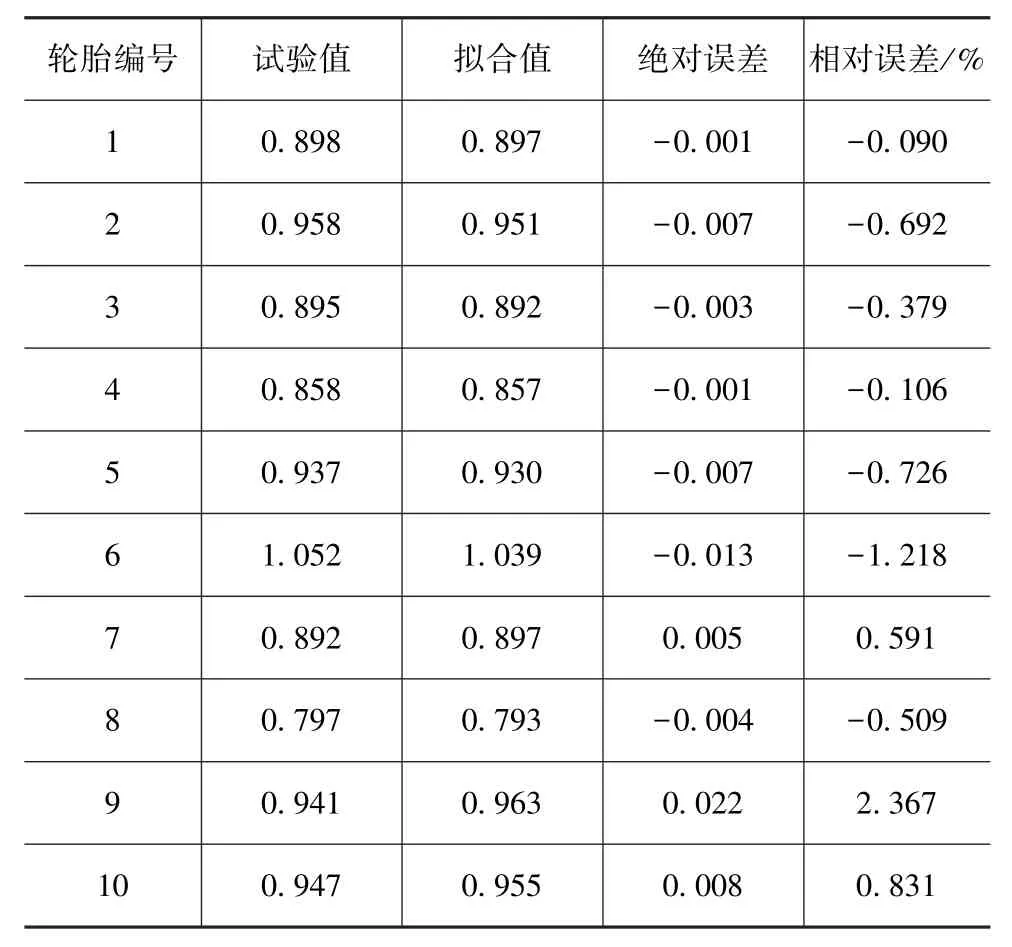
表7 滚动阻力系数回归方程拟合误差
参照上述步骤,进行轮胎干制动距离的PLSR分析。经过 Bootstrap 参数检验后自变量Y4、Y6、Y11、Y12、Y14、Y19共计6 个接地参数通过了显著性检验,得到最终标准化的PLSR 回归模型:
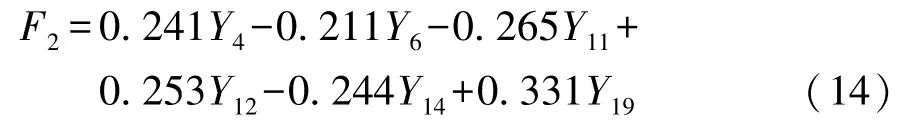
通过比较制动距离的标准化PLSR 模型回归系数的绝对值大小,对制动距离影响作用由大到小的接地参数依次为:中心区横向拉伸应变(+)、外内胎肩接地宽度比(-)、外过渡区横向拉伸应变(+)、内过渡区纵向拉伸应变(-)、外胎肩接地压力偏度值(+)、外胎肩纵向拉伸应变(-)。
将式(14)所示的标准化变量关系还原为原始变量的关系:
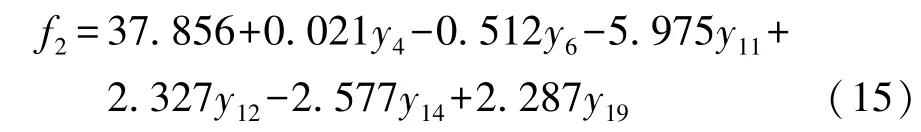
轮胎制动距离的观测值与预测值对比见表8。由表可见,最大相对拟合误差为1.748%,回归方程的拟合效果较好。
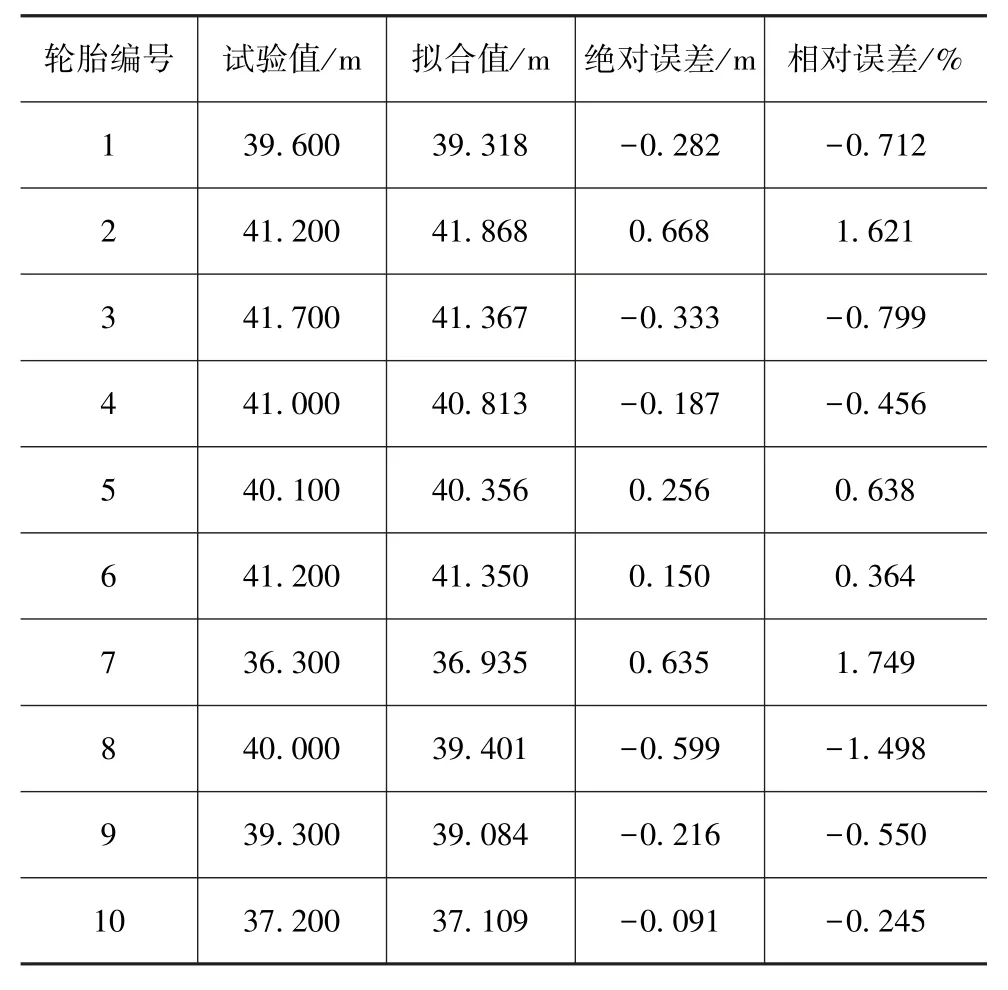
表8 轮胎制动距离回归方程拟合误差
4 结论
(1)对滚动阻力系数影响作用由大到小的接地特征参数依次为:外胎肩XY平面等效应变(+)、外胎肩胎面平均高度(-)、外过渡区接地长宽比(-)、外过渡区横向拉伸应变的偏度值(+)、外内过渡区平均接地压力比(-)、内过渡区XY平面等效应变(+)、外过渡区胎面平均高度(-)。
(2)对轮胎制动距离影响作用由大到小的接地特征参数依次为:中心区横向拉伸应变(+)、外内胎肩接地宽度比(-)、外过渡区横向拉伸应变(+)、内过渡区纵向拉伸应变(-)、外胎肩接地压力偏度值(+)、外胎肩纵向拉伸应变(-)。
(3)提升轮胎的抓地性能须降低接地区胎面Y方向的拉伸变形同时增加X方向的拉伸变形,但随着X方向拉伸变形的增加轮胎滚动阻力也会增加,这导致了滚动阻力和抓地性能的矛盾。
