解锁数据辨析技能 指向思维纵深处

蔡小瑛

小学数学期末检测中统计知识考查中。一向被老师认为得分率最高的统计题，因为加入了数据分析并合理推断这一题型，成了多数同学失分的阵地。

由于小学生生活经验积累少，对于信息的捕捉能力比较薄弱，无法正确的找到问题的核心内容，导致面对一堆的信息无从下手。在这样的处境中，不能提出解决的有效方法，单凭没有根据的猜测，导致一些错误的结论。本文将以人教版五年级“掷一掷”为例，解析小学生数据分析的综合能力。

一.核心問题引思辨“究”寻方向

核心问题是引领数学思考的航标。一节数学课，如果教师能够围绕核心问题组织学生进行学习，学生的思维就有了聚焦点、有了主线。为此，提炼“核心问题”，并围绕其开展教学，是值得教师们不断思考与探究的问题。

1.“螺旋式”提问，切准思维起点

“掷一掷”教材原来的设计从两个骰子开始，直接问两个骰子一起掷，有哪些可能？学生还没有进入状态，不清楚问题的目的是什么，也没有兴趣来深入研究这个问题。不妨分三步，环环相扣，问题成螺旋式上上升，逐渐汇集到核心问题聚焦点上。

第一步，由简而入出示简单问题：如果掷1个骰子会有哪些可能性？每种可能性的大小一样吗？得到结论6个数的可能性是相同的。

第二步，承上启下抛出过渡问题：那么2个骰子的点数和有哪些可能？

第三步，直击中心聚焦核心问题：这11种可能性的点数和大小也一样吗？

2.“聚焦式”商讨，剖析思维疑点

通过“螺旋式”问题，课堂已经有了要解决的核心问题，掷2个骰子点数和的可能性一样吗？如何有效的聚焦核心问题，为此在设计“掷一掷”开始中内容安排上先设置了定规则这一个环节：

教学片段一：定规则

核心问题引领：如果男生和女生用这两颗骰子一起掷，怎样设计一个公平的游戏规则呢？

学生发表意见，先确定点数和的范围，2—1点数2共有11可能。

核心问题聚焦：11种结果，规则怎么定？

规则一：2、3、4、5、6、7男生赢 8、9、10、11、12女生赢

规则二：2、3、4、5、6、男生赢 8、9、10、11、12女生赢

规则三：2、3、4、5、10、11、12，则男生赢 6、7、8、 9，则女生赢

通过核心问题的引领，学生很好的聚焦在怎样来制定一个合理的游戏规则，在小组讨论规则的时候，主要考虑的是把这11种可能尽量平均分。通过商讨，搓议，在思维的碰撞中，得到结论。

3.“互动式”实践，厘清数据真相

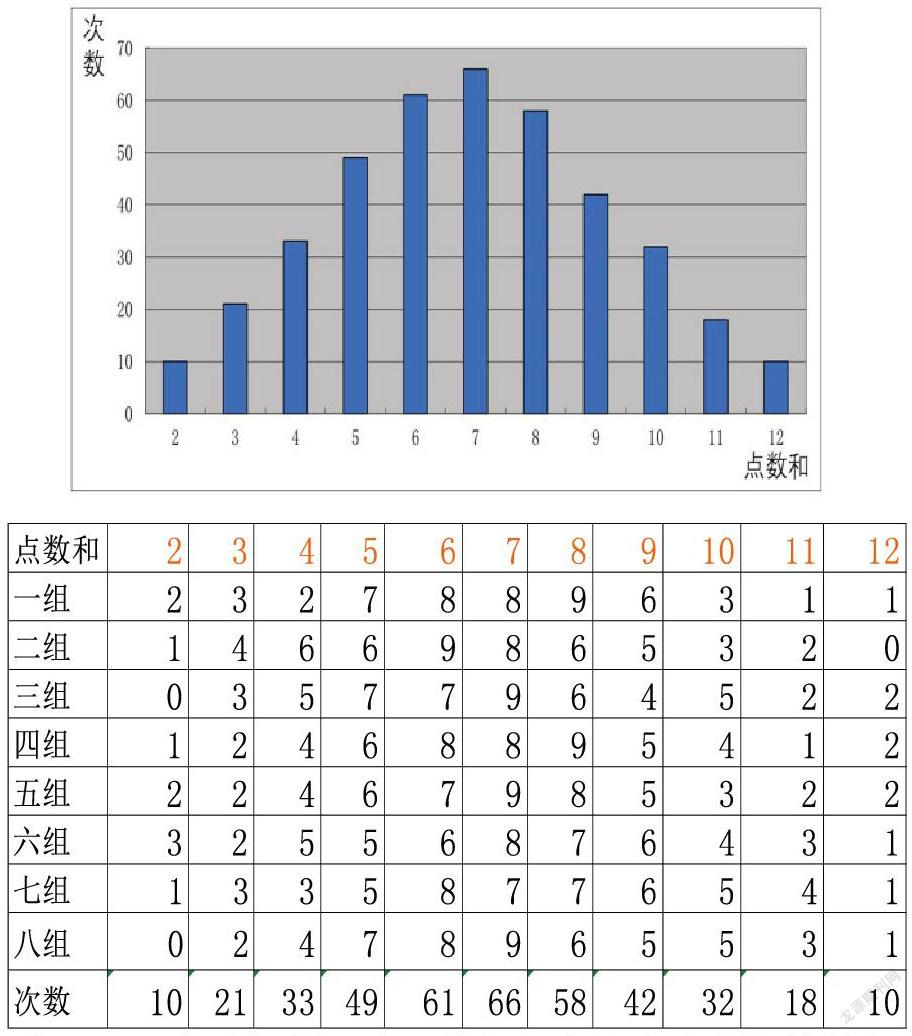
学生通过实践操作，从而获得了大量真实的原始数据，接下来需要对每个小组采集的数据进行整理和汇总，每个小组长汇报实验数据，所有的投掷情况 。

当每个组的实验数据汇总为统计表时撩起了学生的探究欲，也为后面的数据进一步深加工打下了基础。

二.归纳推理获规律，“究”其本质

学生通过观察实验数据，意识到不同，点数和出现的可能性是不同的，教师还要对学生进行数据分析的知道，及时引导学生通过运用学过的方法。

1.合理判断，激活思维“观察力”

从经验到知识，学生学会了合理判断，在辨析中寻找结论，对问题的考虑就全面周详了。

教学片段二：找规律

学生1结论：7出现的次数最多，2和12，3和11，4和10，5和9，6和8为一组，出现的次数相同。

学生2：结论：7出现的次数最多，2和12，出现的次数最少。

学生3：结论：点数和为7的最多。11种点数和一共有36种可能。

通过上面的数学实验使我们了解到判断一件事情可能性的大小，首先要枚举出所有可能性的情况，然后数出发生这件事情的可能情况的个数，出现情况的个数越多，可能性越大，反之越小。

2.动静结合，推动思维“判断力”

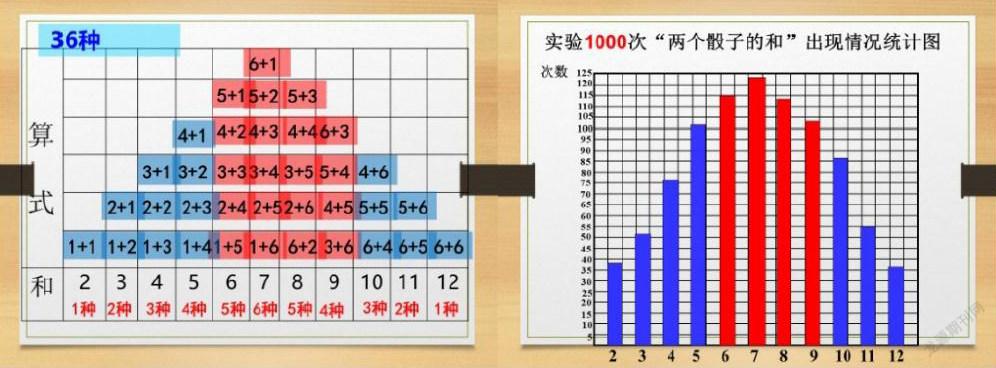
这11种点数和的背后竟然隐藏了36种不同的组合。而在这36种情况里面6、7、8、9、种点数就占24种，而其他的2、3、4、 5、 10、 12只有12种。通过“静”态寻找内部的规律，充分激发了学生的思维判断力。

课堂上全班掷了近400次，但是与真实的概率之间还存在一定距离，如果掷1000次会成为怎样的情况的，通过图示、列举、分析等有效方法，慢慢找到了核心问题的本质。由此可见，数学实验使学生在实践中不断的积累了经验，对突破了数学分析的难点起到了很好的效果。学生通过思辨和观察推断出1000次和400次的结论基本一致。

3.优中内化，完善思维“综合力”

数学知识是比较抽象的，动手操作能够给学生提供直接支撑。实验积累的活动经验，因思维而发生质变，转化为一种静态的反思成果，也成为思维的新起点，让学生在学中思，在思中悟，在悟中得，通过不断地调整，重建，个体的认知才能得到持续的优化。

教学片段三：选规则

回归核心问题：回到之前定的三个规则，你们觉得公平吗？

规则一，男生有21种，女生15种，不公平

规则二：男生有15种，女生15种，公平了

规则三：男生有16种，女生20种，不公平

优化一：2、3、5、6、7男生赢;4、8、9、10、11、12女生赢。

优化二：只要每边的可能性为18种，就公平啦。

优化三：通过实验证明了11种组合有36种可能性，那么要设计一个合理的比赛规则只要两边的可能性是一样就公平了。

来自内驱力的学习过程对于学生的可持续发展是十分有成效的。学生经历每一次实验，头脑中或多或少会形成一些数学活动经验，通过反思比较梳理，补充，完善向高层次的经验转化。当学生积累实践经验和悟出数学思想方法之后，教师还需要引导学生们哲理而行，充分运用反馈、归纳、等活动活动中使其得到真正的提升，经由数学化、逻辑化，构建和完善自己的认知体系。

参考文献：

[1]罗晓敏.指向小学生数学数据分析能力培养的项目化学习策略探究[J].新课程，2021（47）：69.