基于经验的单元整合 促进知识的深度融合

鲁乐芳

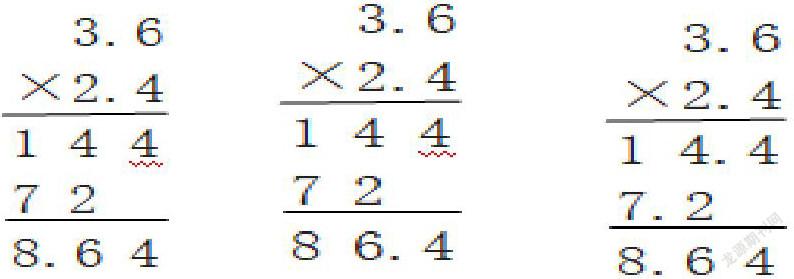
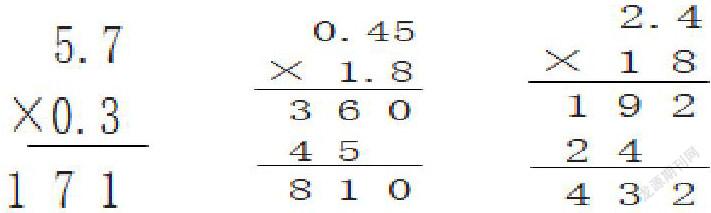
【摘要】 高效、和谐的课堂是现代课堂不懈的追求，课程整合是实现这一目标的有效路径。教学中，教师要摒弃以知识为中心的教学，从学生的认知经验、智理水平和思维方式出发，合理、有序地设计立体式的教学，帮助学生构建完整知识体系，促进学生真实学习的发生，以提升学生思考的广度和深度。本文以“小数乘法”单元整合为例，通过学情分析，梳理单元知识间的关联：“重构教材，让知识走向体系化;沟通联系，让思维走向结构化;抓住本质，让教学走向深度化;拓展创新，让数学走向完善化。”引导学生系统化的建构知识，达到单元知识的深度融合。

【关键词】小数乘法 單元整合 深度融合

小数乘法是小学数学计算教学中的一个重要内容：“怎样让学生能更好的理解算理与算法，启迪学生的思维？怎样让学生具备良好的运算能力，养成良好习惯？怎样在数学活动中积累丰富经验，形成有效的学习方法？”这些都是我们计算教学中所关注的问题。本文从整体上分析计算教学的特征，对教材进行有机整合，积极探寻促进学生思维发展的核心问题，以实现计算教学体系中算理之间的深度融合。

一、前测分析学情，立足现实起点

对于课程设计思路，课标明确提出，既要关注学生的心理特征、分析其认知规律，也要把握住数学这门学科的本质，在呈现数学结果的同时，引导学生利用前期积累的经验，从真实的情境中提取有价值的数学问题并构建模型，一步步探寻解决问题的方法。因此在对小数乘法整合前，我们对学生的学情、教材编排进行分析，以便寻求合理的整合途径。

1.学情分析，找准起点

学生对小数乘法掌握情况如何？为探明教学实际基础，真实了解学生的需求，课前抽取了五年级同一任课老师所教的两个班学生进行了小数乘法的前测。

前测目的：在缺少实际情景背景支撑的条件下，学生对小数乘法形成了怎样认知，具备了何种表征能力，鼓励学生在解决问题时能运用多样化的方法，测试学生的数感、表征能力以及创新能力。

前测对象：五（1）、五（2）班全体学生

前测方式：无提示笔试+后期访谈

本题组从测试中我们可以看出：

（1）学生算理自主表征能力较弱

在计算第一题时，只有85%的学生得到了正确答案，能运用两种或多种方法做题的学生占比为25%，比如用乘法的意义、积的变化规律、乘法分配律、加计量单位计算等以前学过的方法。在表达算理时，只有3个学生采取了画图的方式，这意味着具备发散思维的学生数量并不多，学生不能够利用知识迁移解决没有学过的问题，大部分学生的数感、表征能力有待提升。

（2）学生对算理理解模糊不清

第二题的正确率为45%，明显低于第一题，在前测卷的错误例题中我们发现有些孩子在竖式下面还会出现小数点，我们对这些学生进行访谈。

问题：在竖式下面也出现小数点了，你是怎么想的？

生1：因为在2.4乘13中，3乘以2.4等于7.2，1乘以2.4等于2.4，7.2加上2.4就等于9.6。

生2：因为我们学过整数乘法，在整数乘法中，我们是要一个一个数字往上乘的，第一个数乘出来等于7.2，第二个数乘出来等于2.4，乘法算式是要隔一位对齐的，所以个位是2，十位7加4，等于11，写一进一，百位2加1等于3，总共是312，前面有一位小数，所以是31.2。

从这两位同学我们可以发现，他们受前面小数乘一位整数的影响，觉得每一次乘出来的结果都要写上小数点。第一位同学是忽略了2.4乘以13中1乘以2.4，其实是10乘以2.4，结果是24，最后应该是24加7.2。第二位同学虽然结果正确，但是中间的原因也是一知半解。因此在小数乘法的竖式教学中我们需要做到“理法”并重，不但要帮助学生理解算理，同时也要明晰算法。

（3）粗浅模仿，创新意识较弱

与第2题相比，第3题正确率明显偏低，只有35%的学生做对。其中既有竖式错误，也有积的小数点位置错误。这意味着对于大多数学生而言，只是关注了表面现象，他们只是记住了在小数加减法中要对齐数位，因此迁移到小数乘法时，误认为也需要对齐末位，没有深层次的对比分析，抓住知识的本质特征，只是依靠数感解题，创新意识较为薄弱。

2.抓住关键，确定方向

综上所述，我们考虑教学实际，对目前小数乘法知识整合中做到一个“贯穿”和一个“回归”。

（1）贯穿：把计数单位贯穿算理教学始终

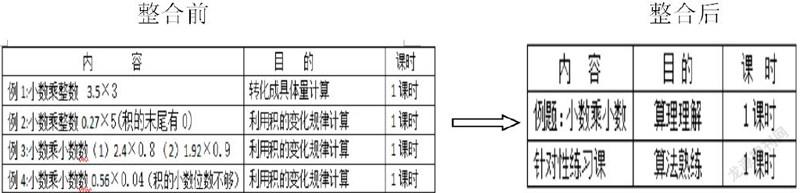
从教材编排分析，小数乘法的计算分 4个例题展开教学（如下图）：

这样编排的主要意图是降低难度、减缓进度，给予学生更多的算法熟练时间与应用。然而小数乘法实际上是由整数乘法演进而来的，它并不是孤立存在。因此在教学中我们将小数乘法的4个例题进行整合，让原本相似的小数乘整数和小数乘小数的教学流程在单元起始课中进行统构，并对整数乘法中计数单位进行深挖，把小数乘法置于整个计算新教学体系之中，用计数单位相乘的思路来整体架构，运用转化思想把小数与整数两种乘法之间的算理进行融通，进一步加深对小数乘法算法的理解，从而减轻学生的思维负担。

（2）回归：以整数乘法为切入点，落实思维主线，回归知识本质

学生对数学知识的理解始于主动地探索，我们在分析学情时明显发现，有些学生不具备良好的创新意识，把小数与整数、小数相乘这两项内容进行整合，改变了传统教学的思路，鼓励学生大胆尝试，积极探索，有机整合演绎推理与类比推理，弄清算法，探明算理。当学生对小数乘整数的算理有了深刻理解，对积的位数变化进行观察，分析积与因数位数之间存在怎样的联系，再猜想他们之间的关系，通过类比推理验证，得出小数乘法的一般计算方法，真正抓住知识的本质。

二、梳理整合内容，重构单元框架

基于以上思考，在整体遵循教材逻辑顺序的同时，进行适当的整合与拓展，形成本单元整体框架。

通过单元重构构建更加合理的教学序列，用一课时新授小数乘法改变了原有教学的重复性，让学生感受到学习挑战性，让各个部分知识相加产生大于整体的效果。

三、研磨教学设计，落实整合内容

前测、课前思考等教学实践活动结束之后，从学生已经熟练掌握的整数乘法的算法与算理为切入点，运用计数单位来建构小数乘整数、小数的算理，形成完整的算理结构。

1.重构教材，让知识走向体系化

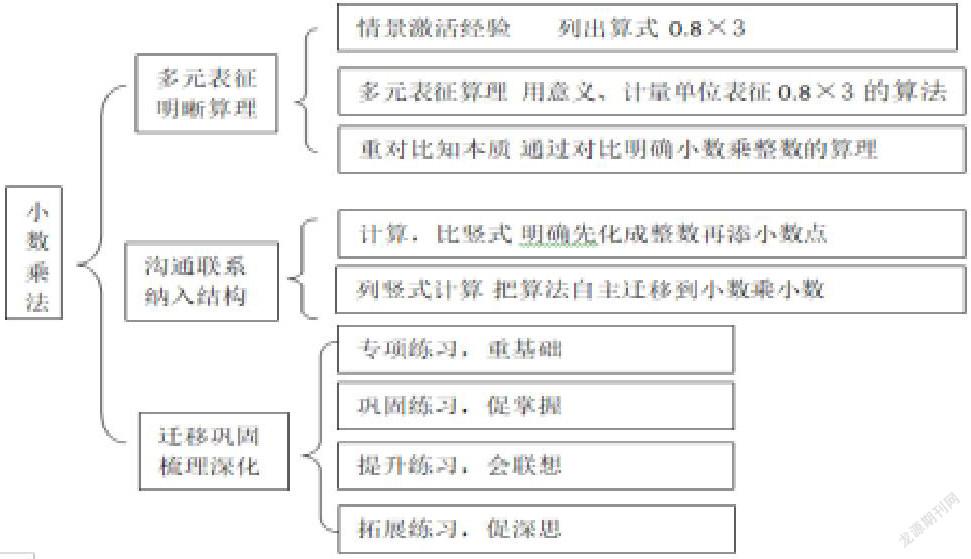
整合小数乘小数、乘整数，在整个教学流程之中既要关注学生产生了怎样的困惑，也要分析教材有哪些难点，把这些内容安排到教学活动中，形成了如下图所示的设计意图。

从中可以看到，通过小数乘整数的算法让学生对算理产生一定的感知，在“竖式”中体现出计算原理，使“积的处理”问题得到解决。有了这样的铺垫之后，带领学生分析在小数乘法计算中，运用竖式应该怎样对两个因数进行对位，由此分析积的定位方法。这样的设计一步步进行，让教材在编排方面存在的欠缺得到弥补，帮助学生消除困惑。

2.沟通联系，让思维走向结构化

计算教学就是要让学生理解算理，为了突破这一难点，在教学设计环节，教师要对学生原有的知识、经验等有所把握，为教学找到合适的起点，又能使学生根据已有的知识自我提出问题，充分表达自己的思考和发现。因此，教师要架构一些辐射性问题，让学生进行合理的猜想，准确迁移，沟通知识间的本质联系。

[课堂回眸]

师：到底 0.8×3 怎样计算呢？请同学们尝试独立计算。学生独立解决问题后汇报算法。

生 1：我是用加法算的，0.8+0.8+0.8=2.4所以0.8×3=2.4。

生 2：我觉得0.8元就是8角，有3个8角，用乘法就能得到24角，就是2.4元。

生 3：8×3=24，0.8×3=2.4。

生4：我是把0.8当成8个0.1，8个0.1乘3等于24个0.1，就是2.4.

师：刚才同学们提出了好多种思路，老师对其进行了整理，大家看，这几中方法虽然不同，有没有相同之处？

生：虽然这是小数乘法，但同学们都是把小数转化成了整数，然后再计算，用到的式子实际上就是8×3=24。

师：（指着8）那刚才这里的8其实表示的是什么？

生：8个0.1.

师：看来8×3可以帮助我们计算0.8×3，你还能想到哪些乘法算式？并讲一讲计算的道理。

生：800×3就是每份是8个百，共有3份，就是24个百，得到了2400。

0.08×3表示每份是8个 0.01，共有3份，一共有24个0.01，得到了0.24。

0.008×3……

师：大家刚才举出的这几个乘法算式，存在着哪些相似之处？

生：都是先想8×3，计算之后再根据计数单位的个数把小数点点到合适的位置。

师：刚才还有同学是这样做的，你认同那种方法？

……

教师要引领学生建构新知识，一定要让学生固有的经验、前期掌握的知识得到有效利用，让新旧知识互相碰撞。为此，教师要用运用问题情景让学生回忆已有的知识，能运用多种办法自主尝试解决问题，再从这些“不同”表达中寻“相同”计算之理，在汇报与交流的过程中解释算理，培养学生的质疑思辨能力，让学生在合作、沟通的过程中对小数乘整数产生更加深刻的理解，找到方法之间的共通之处，引导学生形成计算小数乘法要将其转化成整数乘法的认识，将学习引入关联结构水平，深刻对算理的理解。

3.抓住本质，让教学走向深度化

教师在引导学生的过程中。既有纵向透视，也要横向沟通，由点入线，由线入面，由面入体。把新知识融入已有的知识体系之中，借助于问题唤醒思维，找到新旧知识在本质上的相通之处，彼此之间形成联系。按这样的思路组织数学教学活动，除了能让学生系统、全面、深刻地理解数学知识以外，也能让他们从宏观上把握住不同知识点之间的联系，让学习变得更有深度。

[课堂回眸]

师：刚才我们通过8×3得到了很多题目的答案，现在如果有这样一题0.8×0.3，跟前面的题目有什么不同，你知道他的结果是多少？说说你的理由？

生：因为8×3=24，0.8×0.3有24个0.01，所以0.8×0.3=0.24。

師：如果我把题目改成3.6×2.4你还能计算吗？请你列竖式算一算。

师：为什么结果不一样，你支持哪个？

生：我支持第一个。因为3.6×2.4， 估大后结果也只有12，不可能是86.4

生：如果把这两个乘数全部扩大10倍，就可以列36×24这个式子，这样一来积与原来相比扩大了100倍，再用得到的积864除以100就可以了，结果是8.64。

生：我们是按照36×24来计算，所以第二个算式中间结果没有小数点。

师：你听懂了吗？谁再来说一说？……

提问：猜一猜，第三个计算的结果写成了86.4可能是什么原因？

生：可能只看了一个因数的小数点。

生：我觉得可能与小数加减法相同，需要对齐小数点。

追问：你的意思就是在小数乘法的过程中，要按同样的方法确定小数点的位置吗？

师：学习了小数乘法以后，我们一起来梳理一下计算思路。

生：在计算小数乘法时，可以把两个因数都当成整数，得到了积之后，在根据计数单位的个数加上小数点。

生：在点小数点的过程中，要根据积的变化规律进行。

生：因数里的小数共有几位，积的小数就有几位。

小结：大家关注了因数与积的小数位数之间存在着怎样的联系，要数一数两个因数共有多少位小数，也就是计数单位的个数，再为积点上小数点。

这一环节教师通过呈现学生的两道不同竖式，放手让学生主动辩“理”。当辩中遇“阻”时，教师适时切入，引导回顾整数乘法，在层层“逼”问中使学生渐渐“明”理，这样学生就能更加清晰地感知到小数乘整数、乘小数这两类不同的计算题之间存在着怎样的联系，弄清计算的本质，要重点计一计共有几个计数单位。

4.拓展创新，让数学走向完善化

教学的目的就是要帮助学生形成完善的知识结构，站在更高的高度分析知识的作用，探明知识的由来，弄清知识的本质。这样不仅可以让知识简单易理解，方便迁移，而且能逐渐的形成整体结构，调整学生学习的方式和提升学生的学习能力，慢慢的学会学习，最终形成素养。

[课堂回眸]

（1）专项练习，重基础：给积点上小数点

小结：刚才我们已经交流了应该怎样为积点小数点，对小数乘法中的两个因数与积进行观察、对比，大家发现了什么？

这个练习环节主要是解决积的小数点的定位问题，涉及各种题型，既又要末尾去0，帮助学生解决计算中的疑难问题。学生感受小数乘法与整数乘法之间的计算本质，以观察对比的方式明白积的定位方法与规律。

（2）巩固练习，促掌握：竖式计算

47×5.6 = 1.25×0.8=  3.4×2.09=

通过竖式计算内化算法、形成 技能，并通过对1.25×0.8和 3.4×2.09的算法说理聚焦计算本质。比较3.4×2.09与2.09×3.41的竖式计算，优化计算方法。

（3）提升练习，会联想：

根据47×5.6=263.2，直接 出下面算式的积或因数。

4.7×56= 4.7×5.6= 0.47×5.6= （ ）×（ ）=2.632

本题组是对基础练习中47×5.6=263.2这道题的再度开发，并通过开放题（ ）×（ ）=2.632深化算理，巩固算法，促进深度学习。

（4）拓展练习，促深思

下面的问题（）可以 用2.6×7.2来列式。

a.小静有2.6元，小名有7.2元，两人一共有多少元？

b.有块木板，它的面积为2.6平方米，在为它刷油漆时，如果每平方要用7.2元，需要用多少钱才能把这块木板的油漆刷好？

根据算式“2.6×7.2”来选择生活情境，并在情境中理解小数乘法意义，再根据情境解决小数乘法的实际问题，通过估算和精算对比感受小数乘法笔算的必要性，体会学以致用。

四、反思教學设计，让整合更有效

回顾并反思小数乘法单元知识的整合，顺着学生学习的路径去思考教师教的路径，学生不但学会计算小数乘法，并且理解了小数乘法的本质，具体来说：

1.自主感悟，在交流中思异求同

学生已经积累了一定的生活经验，能得出“0.8×3”的正确结果，把这样的问题融入真实的问题情境中，鼓励学生在解决问题的过程中尽量运用多种方法，并对算理进行解释。学生以多种方式进行对比、提问、观察、合作、自主交流，加深对小数乘法意义的理解，进一步弄清算理。

2.竖式对比，在关联中辨析明质

在计算“0.8×3”时，列竖式过程中遇到了“末位对齐”还是“相同数位对齐”这样的问题，经过辨析之后弄清本质，让学生能把整数乘法数位不对齐的经验运用到新知识点，找到小数乘整数与乘小数之间的对应关系，使学生在“知其然”的基础上能弄清“所以然”。更有价值的是，学生能通过辨析对计算本质产生深刻理解，知道计算就是要计、算计数单位有多少个。

3.分层练习，在梳理中提升素养

组织学生练习不能盲目，要体现出层次性，这样的练习能让学生理解算理，也能实现算法的巩固，这些都有利于学生计算水平的提升，是发展数学思维的有效路径。在计算的过程中学生纠错、整理，能把小数与整数相乘时运用的基本算法进行梳理，把“理”与“法”整合到一起。渗透转化思想，让小数与小数相乘方面的问题得到解决，新旧知识之间的联系会更加紧密，知识脉络变得清晰，运算能力也能增强。同时，变机械的计算练习为深度的学习思考，在层层递进式的解题过程中让学生感受数学之理、数学之趣，激发学生对数学学习的热情。

参考文献：

[1]王昊焱，王彦伟.换个角度算“小数乘法”[J].中国多媒体与网络教学学报（下旬刊），2020（10）：6-7+16.

[2]乔善娟.单元类别教学在课堂中的运用[J].小学科学（教师版），2019（07）：116.