数控机床进给伺服系统模糊PID控制算法仿真研究

2021-01-12赵熹

工业加热 2020年12期

赵熹

(陕西国防工业职业技术学院，陕西西安 710300)

在计算机技术快速发展的大背景下，将模糊PID控制算法应用于数控机床进给伺服系统能够大由提升机床控制精度，同时也是提升机械生产自动化水平的一项关键技术[1]。然而，当前我国在数控机床控制算法的应用方面与西方先进国家相比仍然存在较大差异，需要进一步加强对于各种控制算法的分析，合理应用生产数据，充分提升基于计算机技术的数据处理效率，为高效率、高柔性的工业生产创造便利条件[2]。

1 数控机床进给伺服系统概述

数控机床进给伺服系统的功能主要在于对机床执行部件的运动速度、运动方向和位移进行控制，具体由电气驱动控制器和机械传动机构及执行部件两部分组成，前者内部结构由检测元件、功率放大器、驱动控制系统、电机等所组成[3]，后者内部结构由传动齿轮、滚珠丝杠、工作台等所组成[4]，具体结构如图1所示。

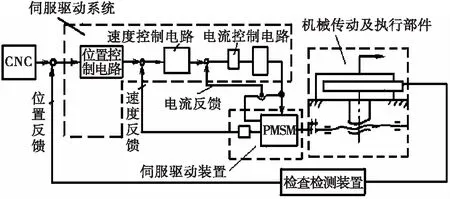
图1 数控机床进给伺服系统内部结构

2 模糊控制基本原理

模糊控制器是模糊控制的基本原理，具体控制流程如图2所示。模糊控制算法的实施步骤为：①中断采样获取被控制量的精确值；②计算被控制量的精确值与给定值之间的误差并获取误差信号E；③将误差信号E输入至模糊控制器，将误差信号精确量转换为模糊量[5]；④通过相应的模糊语言对误差的模糊量进行表示，进而获取误差的模糊语言集合的一个子集E；⑤根据模糊控制规则R和模型矢量E进行模糊决策，进而获取模糊控制量U[6]；⑥对U进行去模糊处理并获取精确的输出量。模糊控制基本原理如图2所示。

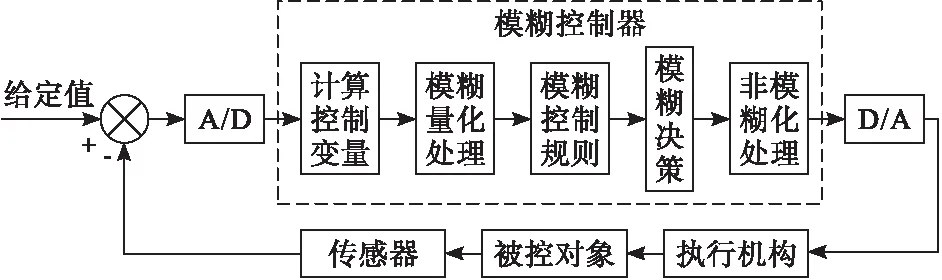
图2 模糊控制基本原理

3 模糊自整定PID控制器设计

3.1 结构设计

传统的三环PID控制器模糊控制方式过于复杂，不适用于位置环和电流环控制。因此，本次研究专门设计了一种速度环PID控制器，将速度误差设置为输入项[7]。由于二维模糊控制器可以将受控对象的动态特性严格反映出来，响应速度更快，控制效果更好[8]，因此将模糊PID控制器应用于速度环，进而建立起一套PID参数自校正模糊控制器，图3为PID参数自校正模糊控制器的具体结构。

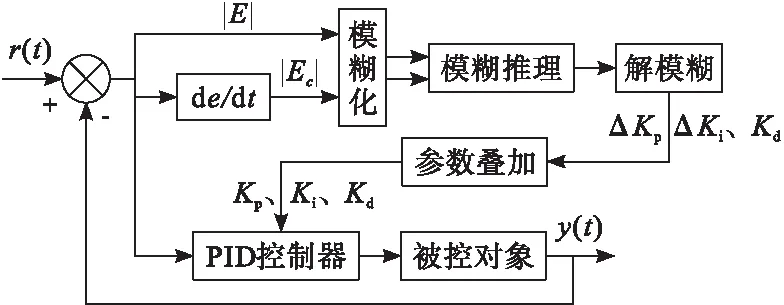
图3 PID参数自校正模糊控制器结构

3.2 定义隶属度函数和输入、输出模糊集

本次研究所设计的模糊控制器属于二维模糊控制器，输入语言变量为|E|和|Ec|，输出语言变量为ΔKd、ΔKi、ΔKp。输出语言变量ΔKd、ΔKi、ΔKp和输入语言变量和的论域值均为“零”(Z)、“小”(S)、“中”(M)、“大”(B)四种。即：

ΔKd、ΔKi、ΔKk、|E|和|Ec|的模糊集为{B,M,S,Z}；|Ec|和|E|的论域均为{0,0.65,0.35,0}；ΔKd、ΔKi、ΔKp的论域值均为{1,0.3,-0.3,-1}。

在此，采用常用的三角形隶属度函数和高斯隶属度函数，图4为与和论域相对应的隶属度曲线，图5为与ΔKd、ΔKi、ΔKp论域相对应的隶属度曲线。

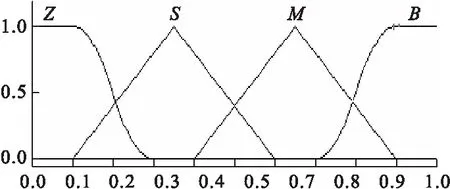
图4 |Ec|和|E|的隶属度函数

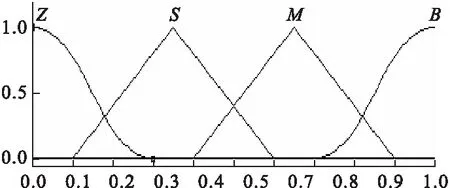
图5 ΔKd、ΔKi、ΔKp的隶属度函数

3.3 模糊控制规则的建立

本次研究将被控制过程对参数Kd、Ki、Kp的自整定进行了规范，具体方案如下：

(1)在较大的情况下，出于系统响应速度方面的考虑，取较小的Kd和较大的Kp[8]。为防止系统超调过大，需要适当地限制积分，因此取Ki=0。

(2)在|Ec|和|E|为中等大小的情况下，为防止系统超调过大，取较小的Ki和Kp。出于系统抗干扰性能的考虑，并防止设定值附近发生振荡，需要Kd的值进行适当的束缚，即在较大的情况下，Kd值取小一些，在|Ec|较小的情况下，Kd值取大一些[9]。

根据大量的试验记录和PID参数整定原则，能够列出输出变量ΔKd、ΔKi、ΔKp的控制规则，具体结果如表1～表3所示。

表1 Kd控制规则

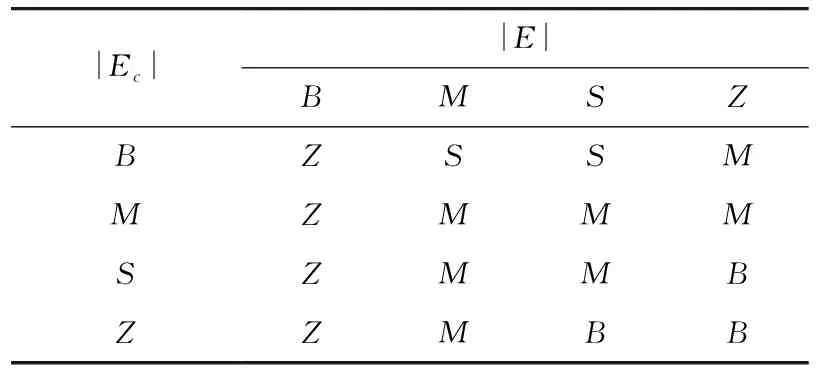
表2 Ki控制规则

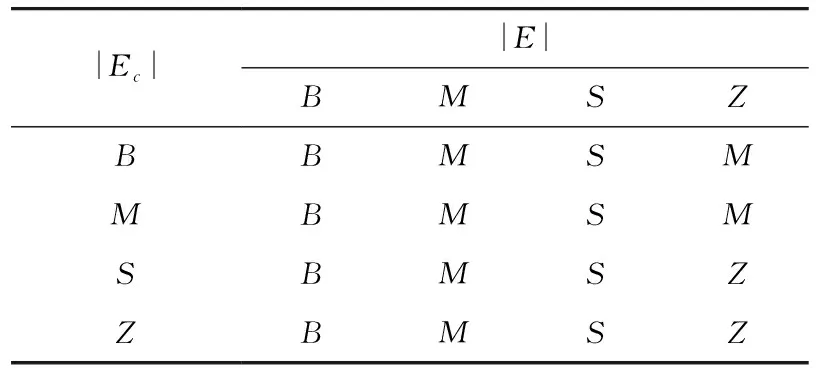
表3 Kp控制规则

3.4 建立模糊控制器

本次研究通过Matlab所内置的FIS对模糊控制器进行编辑，并且设计出一套Mamdani型模糊控制器，分别添加隶属度函数、语言变量名和输入/输出变量名，根据表1～表3添加控制规则，保存模糊控制器并将其存入内存缓冲区。

4 仿真分析

4.1 数控机床进给伺服系统的数学模型

借由磁场定向和矢量变换，可以将PMSM看作为直流电机进行建模，本次研究通过图6来表示数控机床进给伺服系统。

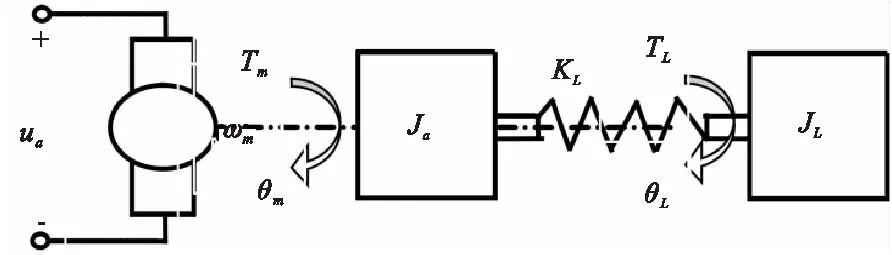
图6 电机-传动轴-负载模型

(1)

(2)

(3)

4.2 仿真结果

本次研究所建立的仿真参数具体如下：电机电阻R=1.0 Ω；电机电感L=0.01 H；电机黏性阻尼bm=0.010 N·m/rad·s-1；电机转动惯量Jm=0.005 km·m2；负载黏性阻尼b1=0 N·m/rad·s-1；负载转动惯量J1=0.15 km·m2；初始PID参数值为Kd=15，Ki=0.03，Kp=35。图7为最终的仿真结果。

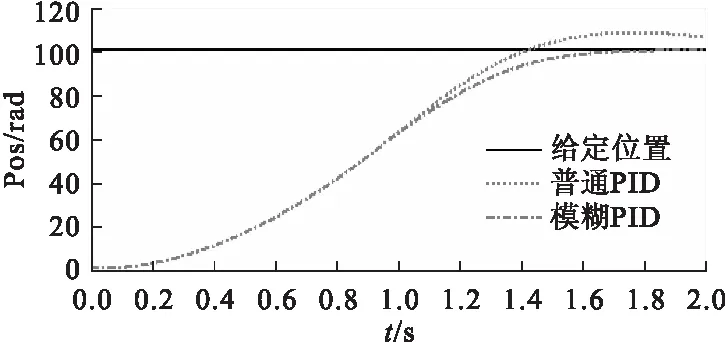
图7 位置跟踪结果对比

根据阶跃响应曲线可以发现，在数控机床进给伺服系统应用模糊PID参数自调整技术，能够加快系统响应速度，减少调节时间，进而实现无超调控制。另外，经实验研究发现，Kd、Ki、Kp三个参数的变化也符合预期，在系统稳定的情况下，对象参数变化和抗干扰能力均体现出了较强的适应性，综合性能明显优于常规PID控制技术。