火箭卫星舱壳体分离灵敏度分析与优化设计

葛 悦，王洪波，龚 旻，赵俊锋，高 峰，罗 波，牛 飞

(中国运载火箭技术研究院， 北京 100076)

为提高运载火箭的运载能力，卫星舱多设计为薄壁结构，在进行分离动作时具有显著的刚柔耦合效应[1-3]。一方面，卫星舱结构需要有足够的强度与刚度，在大冲量分离力作用下能够避免分离过程中各分离体以及有效载荷之间发生碰撞，保证分离过程迅速、安全；另一方面，卫星舱结构质量的增加也将对火箭的运载能力产生直接影响。因此有必要开展卫星舱优化设计，考虑壳体柔性对分离过程的影响，在保证分离安全性的基础上尽量减小卫星舱的结构质量。

以车辆、火炮、船舶等对象，考虑结构刚柔耦合特性的灵敏度分析与优化设计的研究工作已引起普遍关注[4-7]。针对导弹及火箭的分离过程多基于刚体模型开展灵敏度及可靠性分析，岳玉娜等[8]分析了导弹适配器分离的运动特性和安全性。张海瑞等[9]基于刚体模型研究了飞行器级间分离的可靠性。崔奇[10]针对旋抛分离的柔性整流罩进行了仿真与可靠性分析。对于运载火箭卫星舱壳体分离的相关研究工作还有待开展，因此有必要基于刚柔耦合研究卫星舱壳体结构参数对卫星舱壳体分离的影响并进行优化设计。

本文首先根据柔性多体动力学理论，选取卫星舱壳体半罩的结构参数及推冲器安装位置等参数为设计变量，将设计过程中较为关注的卫星舱壳体质量、分离体与有效载荷的最小间隙、半罩分离速度等作为响应量，建立基于刚柔耦合的卫星舱壳体平抛分离参数化模型，采用最优化拉丁超立方实验设计方法构建样本，根据基于方差测度的非线性回归方法对设计变量进行灵敏度分析，获取对分离过程影响显著的重要设计变量。并通过克里金方法(Kriging)构建近似模型，采用多岛遗传算法方法进行卫星舱壳体优化设计，得到卫星舱壳体优化设计方案。

1 卫星舱壳体分离模型

1.1 卫星舱壳体平抛分离

卫星舱壳体结构如图1所示。壳体总高度为2 029 mm，主要由铝合金、蜂窝夹芯及玻璃钢3种材料构成。

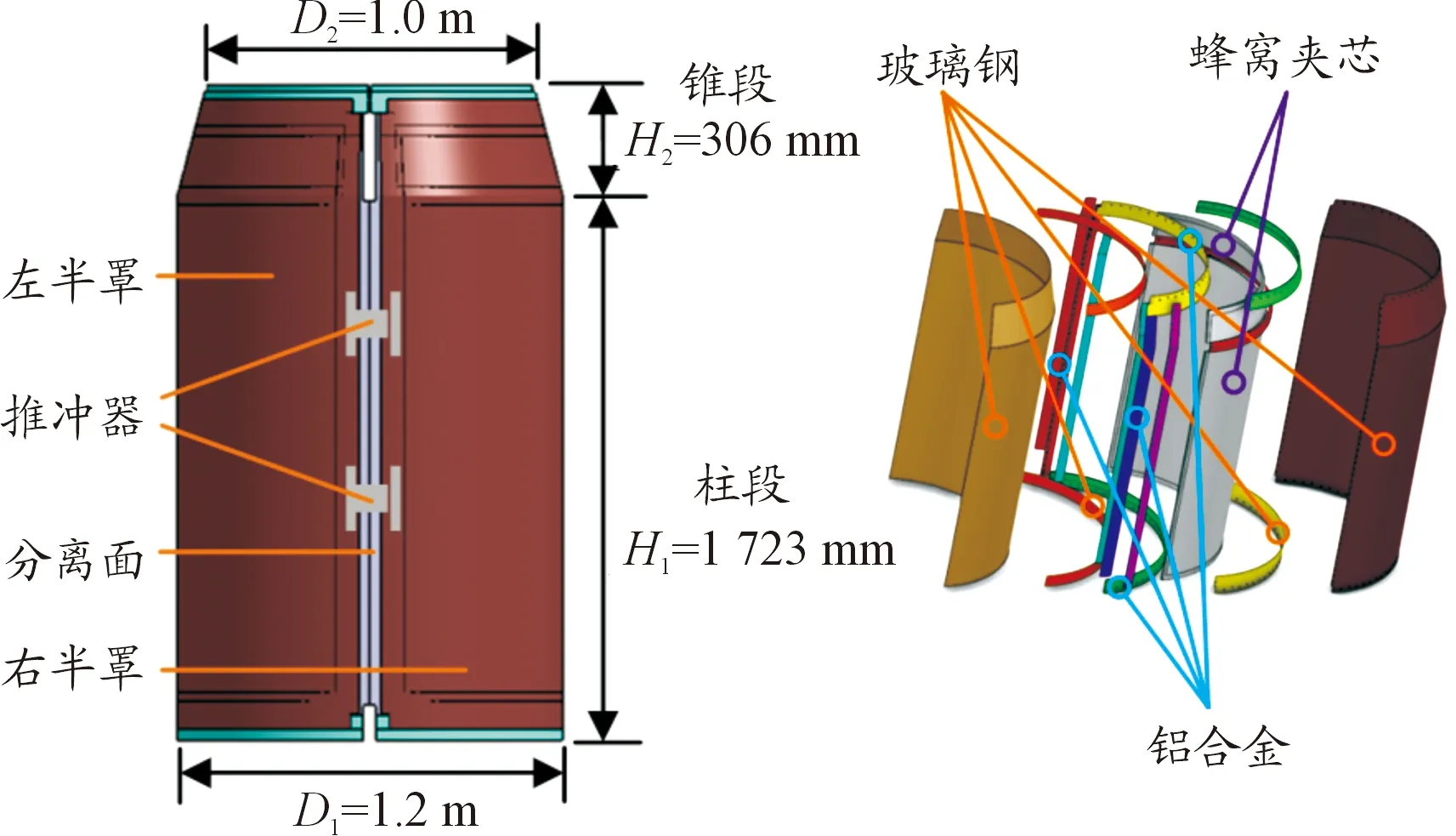
图1 卫星舱壳体结构示意图

卫星舱壳体分离采用如图2所示的线切割平抛分离方式。分离时序发出后，卫星舱壳体首先切割解锁为两个半罩，其次安装在分离面附近的四组推冲器同时动作，将两个半罩相互推离，实现卫星舱壳体的平抛分离。实际飞行时卫星舱分离在真空中待火箭末级发动机关机后进行，因此分离过程中不存在气动力干扰以及过载影响。

图2 卫星舱壳体平抛式分离示意图

1.2 刚柔耦合动力学建模

本文基于柔性多体动力学中的混合坐标法，建立卫星舱壳体平抛分离的刚柔耦合动力学模型。

首先通过模态分析，用各阶模态的线性叠加表征卫星舱壳体的变形运动，并综合其刚体平动、转动及弹性变形，在以壳体质心为原点，坐标指向始终与壳体未变形状态保持一致的浮动坐标系上，建立卫星舱壳体运动的广义坐标为：

(1)

其次根据地面试验建立推冲器力元模型，考虑到进行灵敏度分析时分离载荷工况随壳体设计的变化而变化，采用推力-位移关系表征不同工况下推冲器的推力大小，并通过坐标变换计算广义力Q。

最后根据拉格朗日方程建立刚柔耦合动力学方程为[11-12]：

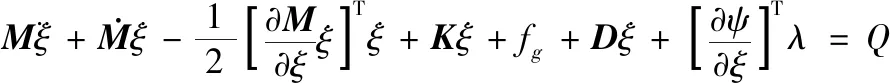
(2)

式(2)中：ξ为卫星舱广义坐标，由浮动坐标系相对于惯性系的位置坐标、欧拉角坐标以及柔性体的模态坐标组成，M为卫星舱质量矩阵，K为刚度矩阵，fg为广义重力，D广义模态阻力矩阵，ψ为约束方程，λ为拉格朗日乘子，Q为广义力。

求解上述方程即可获得卫星舱壳体分离过程中半罩的位置、速度等运动特性信息。

为便于实现灵敏度分析时模型的自动更新，本文基于Python语言建立脚本文件并对ABAQUS进行二次开发，实现卫星舱壳体有限元模型的参数化，基于ADAMS宏命令语言实现卫星舱壳体分离刚柔耦合动力学模型的参数化。

2 分离参数灵敏度分析

2.1 基于方差测度的非线性回归灵敏度分析方法

针对非线性系统Y=g(X)，X=(X1,X2,…,Xn)为n维输入变量，若响应Y对输入变量X的非线性程度较高，且无法确定各变量之间的独立性，采用适于相关变量的二次非线性回归方法进行灵敏度分析[13-14]。抽取N个各输入变量的组合作为样本，为保证分析精度，样本容量应满足[15]：

(3)

各设计变量的取值组成N×n维样本矩阵A和N×n维样本平方矩阵A*2，即

(4)

式(4)中，xij表示第i个输入变量的第j个样本点。计算样本矩阵A的输出响应，可产生N个响应值为：

(5)

响应量的总方差V可按照下式估计：

(6)

(7)

(8)

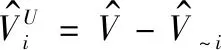
(9)

(10)

(11)

(12)

(13)

输入变量的总贡献率越大，说明输出响应对该输入变量的灵敏度越高。若相关贡献率大，则说明该变量与其他变量的耦合效应较强，出现此情况则需在舍弃设计变量时注意。

2.2 设计变量及输出响应的选取

卫星舱结构设计需考虑承载、透波、分离装置安装、部段连接等各方面约束，结构分区较为复杂。为进行参数化设计，根据各个区域材料分布方式的不同，将卫星舱分为如图3所示的夹芯区、锥柱过渡区、金属加强区、连接区以及分离装置区等5个分区，选取各分区材料厚度(见图3)和分区几何尺寸(见图4)参数及推冲器安装位置参数设置为设计变量，考虑实际加工时锥柱过渡区与夹芯区厚度有连续性限制，不将thickD设为独立变量。共19个设计变量按照表1中设置上下界，同时考虑实际加工工艺限制，对设计变量的取值离散化处理。各变量名称及取值界限如表1所示。

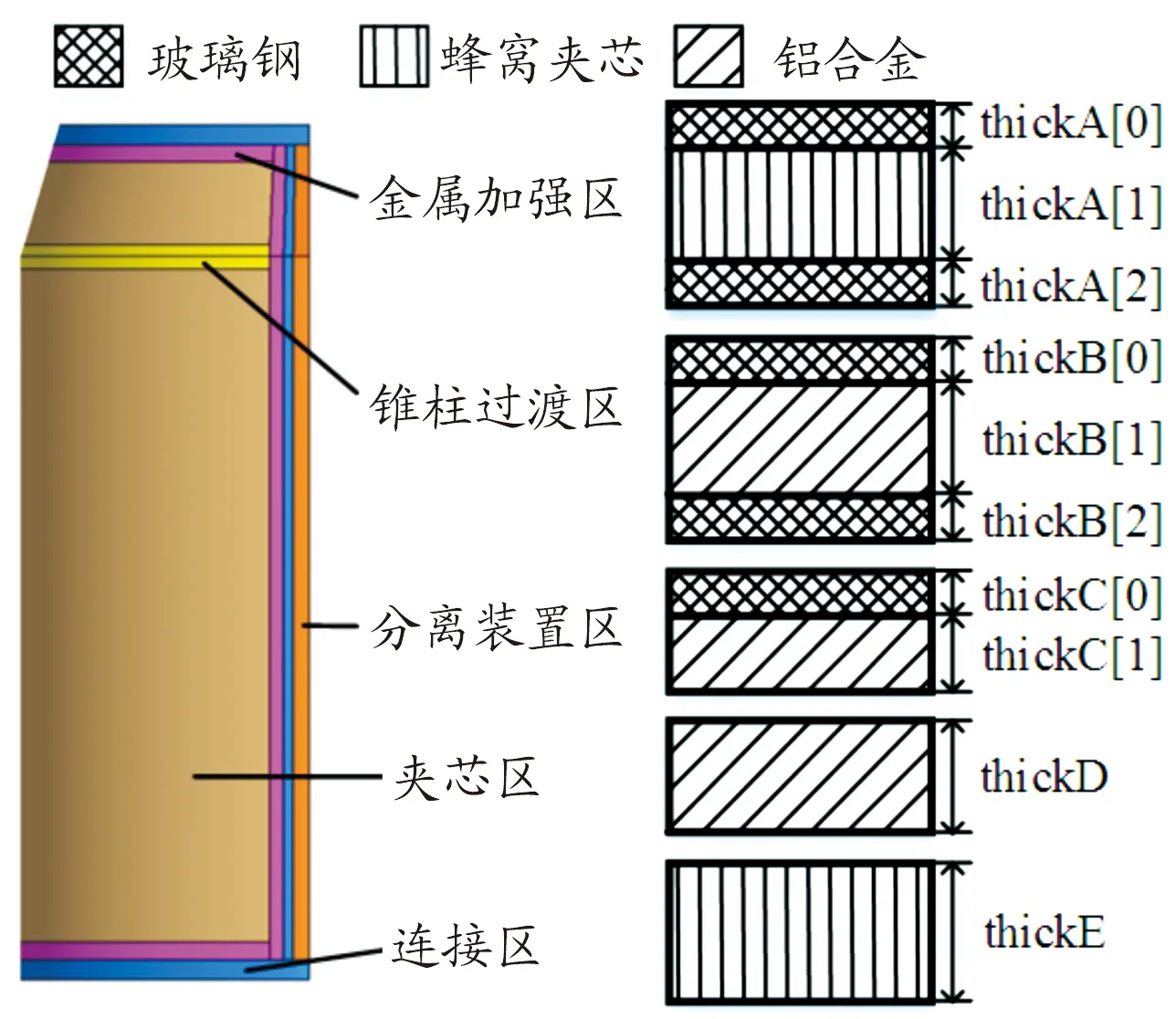
图3 卫星舱壳体分区材料厚度示意图

图4 卫星舱壳体分区几何尺寸

表1 设计变量

将主要关心的卫星舱壳体总质量、分离体与有效载荷的最小间隙、两半罩分离速度等设计变量作为输出响应，如表2所示。

表2 输出响应的选取

2.3 灵敏度分析

2.3.1实验设计

本文选用最优化拉丁超立方(Optimal Latin hypercube design)方法确定实验设计样本，该方法是一种多维分层抽样方法，它在拉丁超立方抽样的基础上使所有试验点尽量均匀分布于设计空间范围内，具有非常好的空间填充性和均衡性，能够使因素和响应的拟合更加精确真实[16]。

考虑式(3)的约束及后续近似模型精度的要求，设置样本容量为1 000。在Isight中通过Simcode模块实现ABAQUS和ADAMS的集成，完成程序间设计变量的自动修改及调用。搭建并运行如图5所示的实验流程，计算输出响应。

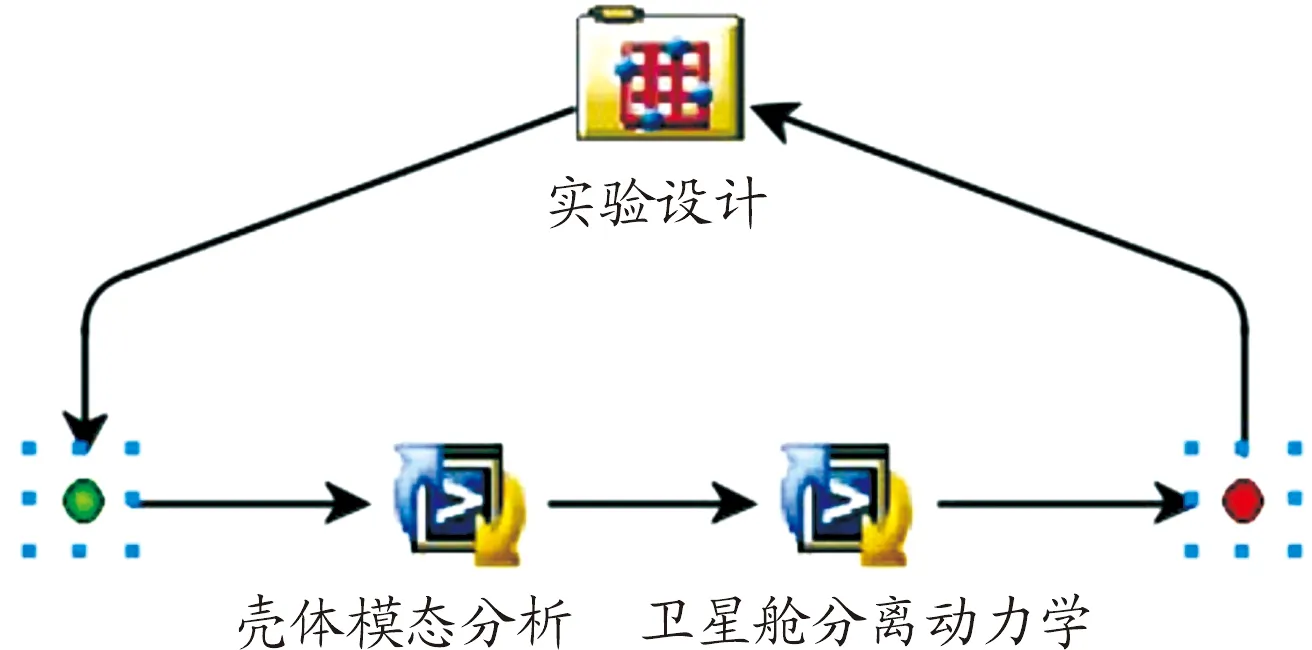
图5 灵敏度分析流程示意图

2.3.2灵敏度分析结果

依据实验设计中样本点的输出响应结果进行灵敏度分析。首先计算设计变量在同一水平下所有样本的响应均值，依次计算出所有水平下的响应均值[17]，可得图6所示的设计变量主效应图。主效应图反映响应受单一设计变量影响的变化情况。由图6(a)可以看出，设计变量对卫星舱总质量的输出响应基本呈线性正相关关系，thickA[2]、thickB[1]、Wid_Angle[2]、Wid_Angle[1]、thickA[0]等设计参数对总质量响应影响显著。从图6(b)中可以看出，设计变量对最小间隙响应呈非线性关系，随大部分设计变量的增大最小间隙先增大后减小，最小间隙响应随着thickB[1]、thickA[1]、thickC[1]、Wid_Angle[2]、thickE等设计变量变化显著。

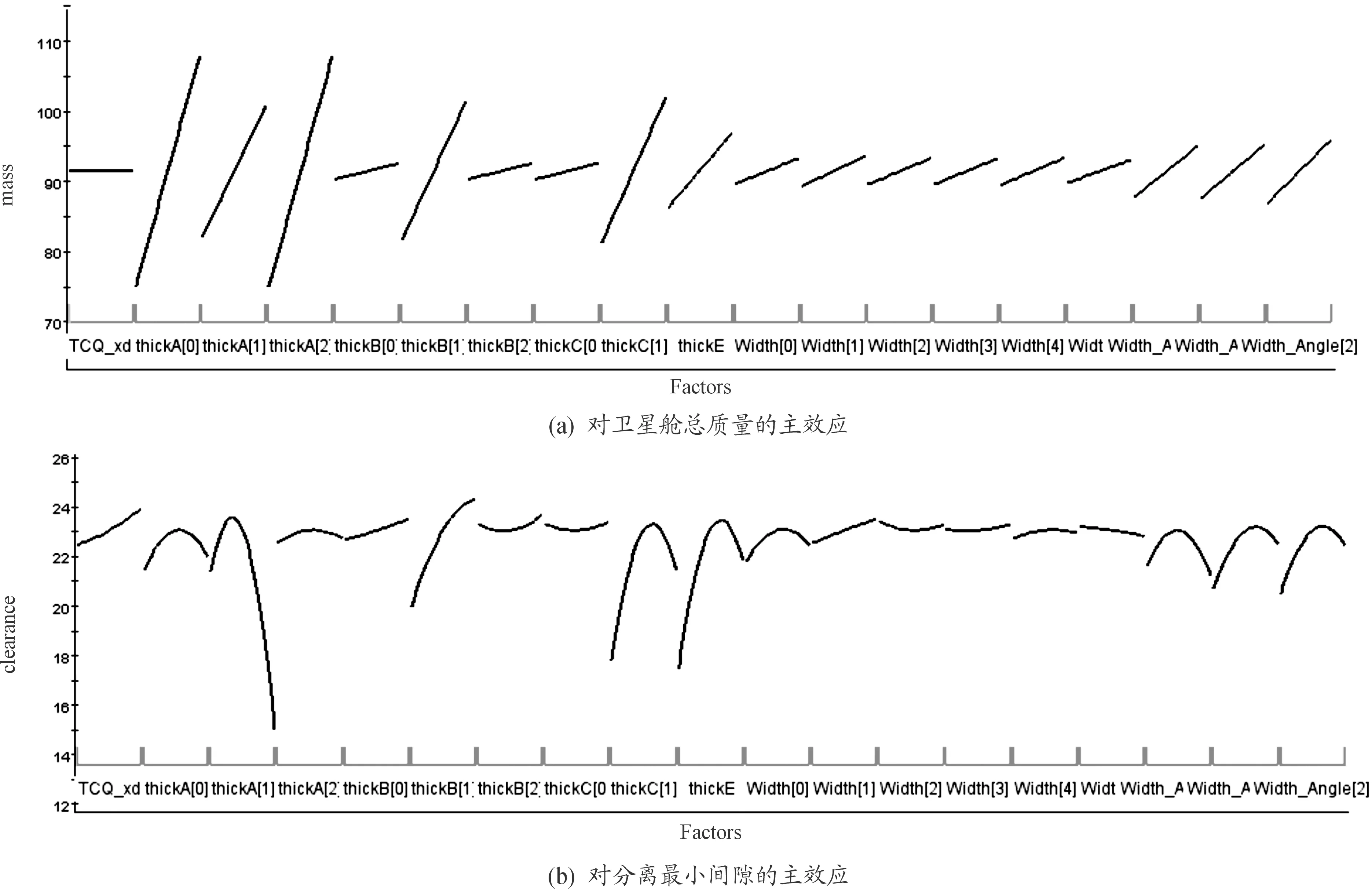
图6 设计变量主效应图

设计变量对卫星舱总质量响应的灵敏度系数如表3所示，从表3可以看出，夹芯区玻璃钢面板厚参数thickA[0]和thickA[2]对卫星的总质量的影响最为显著，两设计变量对总质量响应方差的总贡献率达61%，thickA[1]、thickB[1]、thickC[1]三个设计变量对总质量响应的贡献率均在10%左右，其他变量的贡献率较小，均在5%以下。

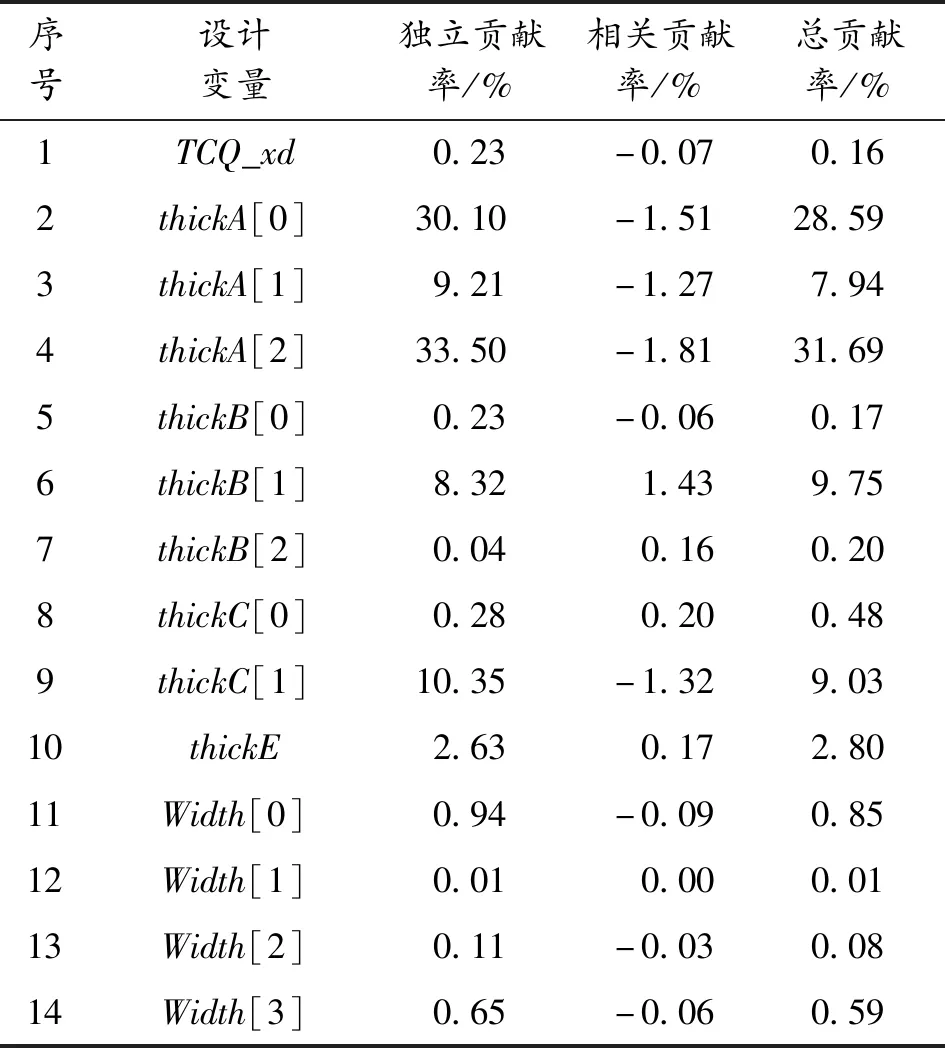
表3 设计变量对卫星舱总质量响应的灵敏度系数

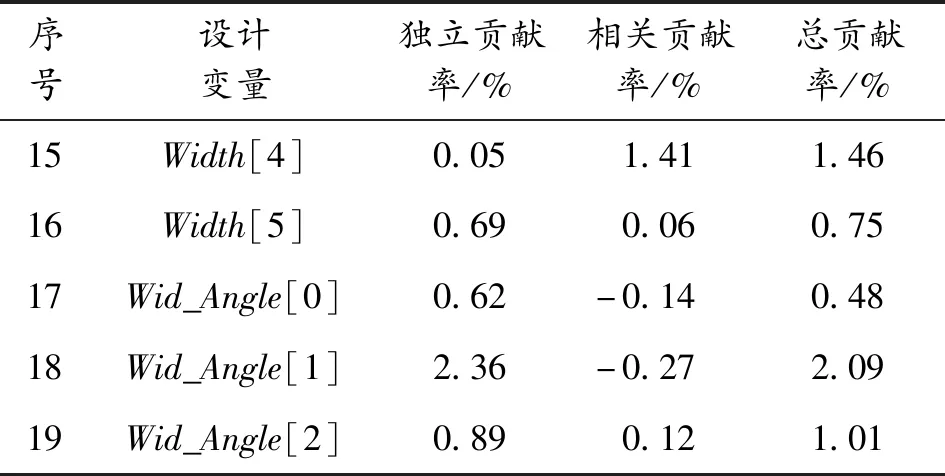
续表(表3)

设计变量对分离最小间隙的灵敏度系数如表4所示，可看出，夹芯区夹芯层高度参数thickA[1]对分离最小间隙的影响最大，响应方差贡献率达42%。thickE、thickB[1]、thickC[1]三个设计变量对分离最小间隙响应的贡献率在10%～20%，其他变量的贡献率较小，均在5%以下。同时各变量的相关贡献率较小，说明各变量间的耦合效应不大，可以根据总贡献率的大小选择用于优化设计的关键变量。

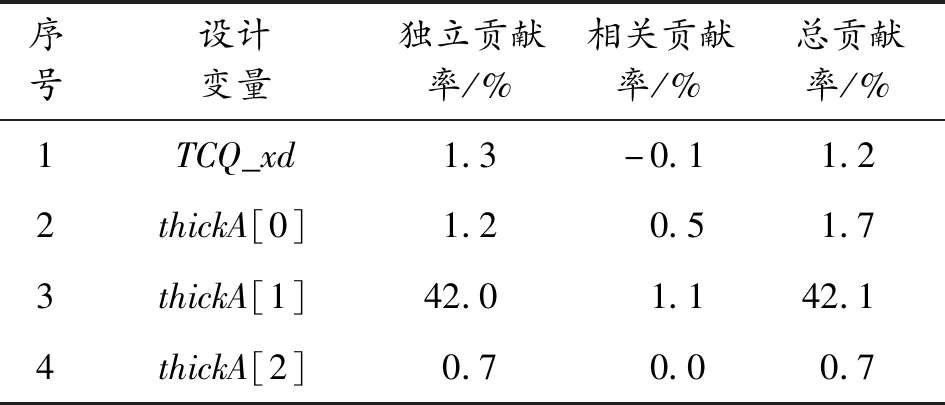
表4 设计变量对分离最小间隙响应的灵敏度系数

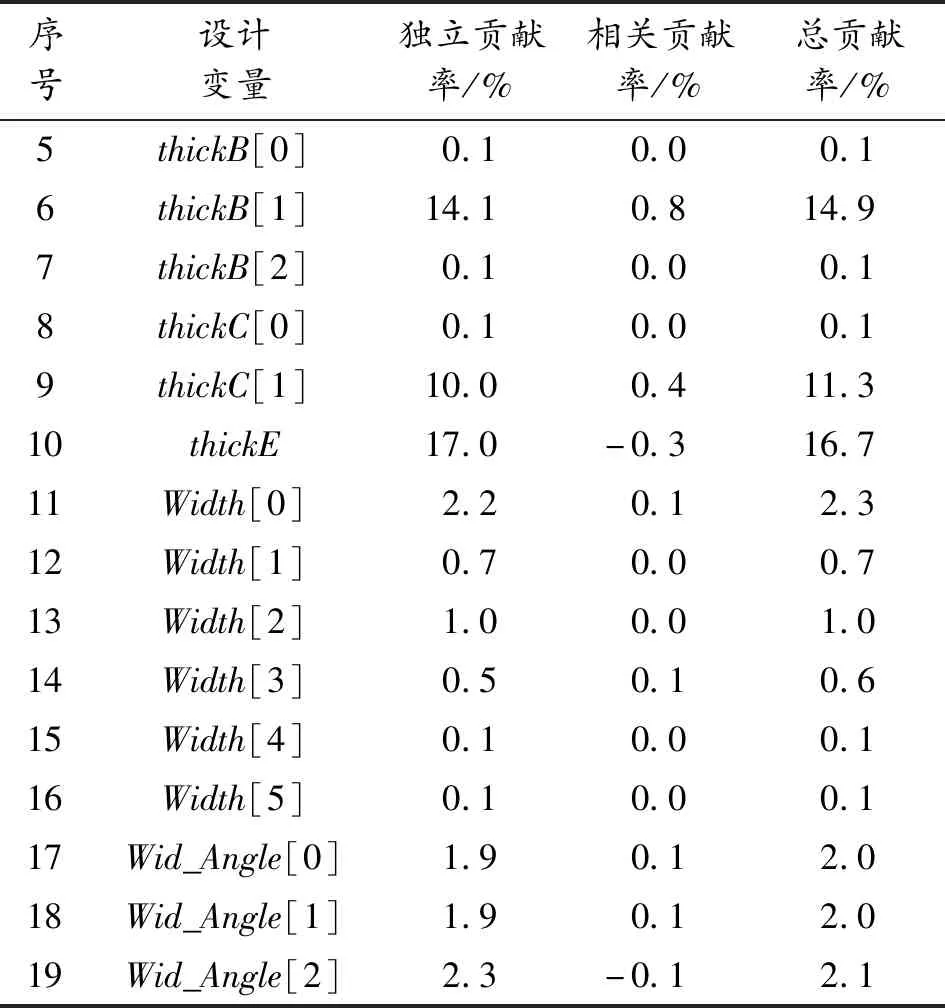
续表(表4)

3 卫星舱壳体优化设计

3.1 优化模型

卫星舱壳体结构优化设计需要以保证分离安全性为前提，首先分离过程中各分离体不能发生碰撞，因此需要对半罩与有效载荷的最小间隙进行约束；同时为保证上面级起控后的安全性，要使半罩在火箭起控前脱离飞行轨迹，可通过对半罩的分离速度进行约束予以保证。因此在建立优化模型时，选取卫星舱总质量最小作为优化目标，约束两半罩平均分离速度不小于3 m/s，最小分离间隙不小于10 mm。

通过灵敏度分析挑选出夹芯区各层面板厚度thickA[0]、thickA[1]和thickA[2]、金属加强区金属面板厚度thickB[1]、连接区金属面板厚度thickC[1]、分离装置区金属面板厚度thickE、连接区周向角Wid_Angle[1]、分离装置连接区周向角Wid_Angle[2]共8个参数作为优化问题的设计变量。灵敏度分析的其他设计变量保持基准值不变。

优化问题可表示为：

(14)

通过灵敏度分析，优化问题设计变量由19维减小为8维，大大简化了优化问题的复杂程度，降低了计算量。

3.2 优化设计

考虑优化所需样本容量大，计算量很大，采用克里金(Kriging)近似模型代替原始模型进行优化设计[18-19]。

近似模型的建立流程如图7所示，首先采集灵敏度分析时计算求得的样本点，作为初始化近似模型，并用另外一部分独立的样本点对比原模型与近似模型所求得的响应输出的差异。采用拟合优度R2衡量近似模型与样本点的符合程度，R2取值在0～1，越大说明近似模型拟合程度越好，R2值大于0.9，则表示近似模型可信。若可信，则用近似模型代替原模型进行优化设计，若不可信，则将用于验证的样本点更新近似模型，再进行检验，直至近似模型可信为止。

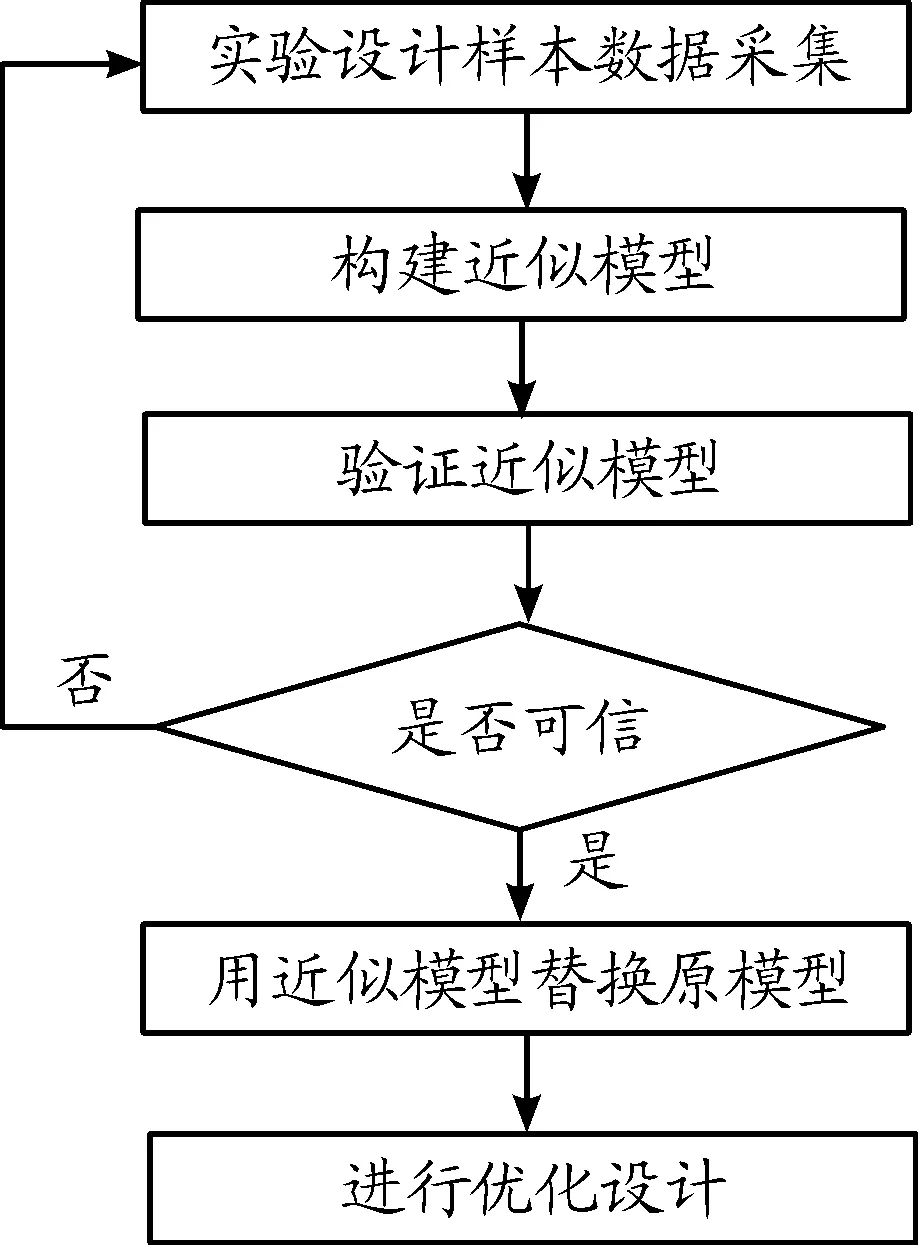
图7 近似模型构建流程框图

考虑分离最小间隙与响应输出之间的为非线性关系，采用多岛遗传算法(MIGA)进行优化设计。相比于传统遗传算法，多岛遗传算法将一个大种群分成若干个子种群，即“岛”，不同岛上的子种群之间通过迁移完成个体交换，增加个体多样性，因此它具有比传统遗传算法更强的全局求解能力和计算效率[12]。多岛遗传算法的各参数值如表5所示。

表 5 多岛遗传算法参数

3.3 优化结果检验及分析

用近似模型通过多岛遗传算法进行优化，得到的各设计变量的优化结果如表6所示。同时将优化后的设计变量作为输入，带回原仿真模型中进行检验，对比近似模型和原模型的输出响应如表7所示。

表6 设计变量的优化结果

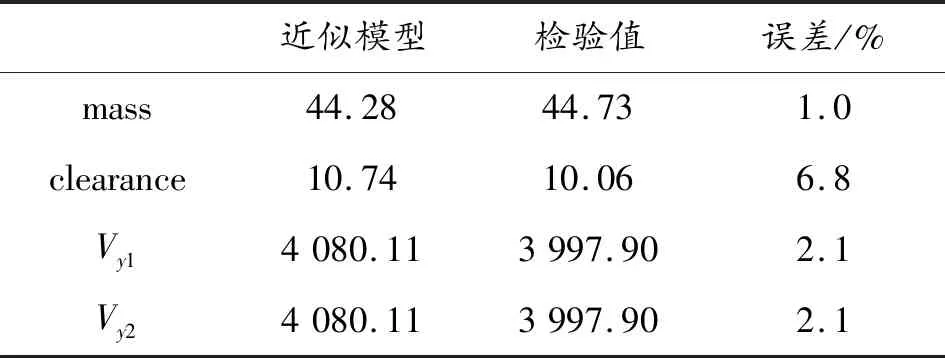
表7 优化结果检验

图8为优化目标卫星舱壳体质量的优化历程曲线，通过优化卫星舱壳体总质量从初始的85.58 kg减小至44.28 kg，减重48.3%，同时满足分离最小间隙不小于10 mm，半罩平均分离速度不小于4 m/s的约束条件，保证了卫星舱分离的安全性，优化结果满足设计要求。

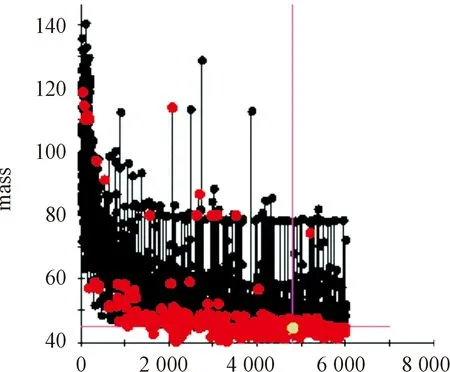
图8 卫星舱壳体质量的优化历程曲线

表7中对比了原模型输出与近似模型输出，近似模型输出响应误差不超过7%，证明优化结果有效，其中分离最小间隙的误差较大为6.8%，说明设计变量与输出响应的非线性效应一定程度上会影响近似模型的精度，后续可考虑进一步增加建立近似模型的样本总数以提高输出响应的精度。

4 结论

1) 夹芯区各面板厚度thickA[0]、thickA[1]和thickA[2]、金属加强区金属面板厚度thickB[1]、连接区金属面板厚度thickC[1]、分离装置区金属面板区厚度thickE、连接区周向角Wid_Angle[1]、分离装置连接区周向角Wid_Angle[2]等参数对分离过程和卫星舱壳体总质量影响显著，是进行卫星舱分离设计和结构设计时需要主要考虑的设计变量，其他结构参数的影响较小。

2) 夹芯区夹芯层高度参数thickA[1]对分离最小间隙的影响最大，响应方差贡献率达42%，是影响壳体结构刚度的关键因素；

3) 通过优化设计，卫星舱壳体质量可在保证分离安全性的前提下减少40%以上，提高了火箭有效载荷运载能力。

目前优化后的卫星舱壳体强度虽满足使用工况要求，但剩余强度系数有所下降，在面向工程应用时，应充分考虑卫星舱壳体的强度约束。