寿命指数分布类型装备可靠性指标估计方法的应用分析

魏国东，俞 翔

(1.海军工程大学 动力工程学院， 武汉 430033； 2.陆军军事交通学院镇江校区，江苏 镇江 212003；3.海军工程大学 舰船与海洋学院， 武汉 430033)

检验装备的实际平均故障间隔时间(Mean Time Between Failures，MTBF)是否满足理论值的下限要求，是装备可靠性评价工作中至关重要的活动之一。在种类繁多的舰船装备中，舰船电子元器件装备的维修工作特点比较鲜明，该类部件发生故障一般采用直接更换备件的方式进行维修，如电阻、电容、集成电路等部件。维修工作具有调整时间短、更换迅速等特点，由于受保障性影响因素影响较小，这类装备的故障间隔时间统计较为精确，且近似等价于装备的寿命，因此，通过估计装备的寿命分布参数，便可对该类装备的MTBF指标进行评价分析[1]。常见的装备寿命分布类型有：指数分布、正态分布、威布尔分布等。通过概率模型及统计模型法可以基本确定装备寿命分布类型，在此基础上，运用寿命分布的拟合检验方法可以确定部件的寿命分布类型。

一般，装备的寿命分布类型可通过大量的工程试验确定，这种方法比较可靠、准确。实际中，由于现代舰船装备制造精密、造价昂贵，试验所需时间较长、费用较高，造成收集到的试验数据样本量较小。但是，使用部队和装备维修保障单位累积了大量的故障汇编、历史维修记录。因此通过分析装备使用数据信息来确定部件的寿命分布类型是一种很好的尝试[2]。在实际操作过程中，可以采取观测装备寿命取代做专门寿命试验观测寿命的方法，在舰船装备使用阶段，通过对舰船装备保障维修数据进行收集，获得故障部件的失效前累积工作时间。

1 寿命分布参数估计方法

当装备的寿命分布类型确定后，需要对分布参数进行估计，极大似然估计和Bayes估计是进行寿命分布参数估计最常用的两种方法[3-6]。极大似然估计通过样本确定参数的似然函数，并将该似然函数用于度量参数出现的可能性，一般假设使似然函数取得最大值的参数值即为该参数的估计值。极大似然估计的优点是具有较好的大样本性质并符合人们的直观经验。主要缺点是在样本容量较小的情况下，由于样本中包含的信息较少，使得所估参数值的准确性得不到保障。

Bayes 统计方法与经典统计方法相比最大区别在于它利用了先验分布。Bayes估计认为任何一个未知量都可以作为一个随机变量，可以通过先验分布进行描述。将样本结合先验分布，根据Bayes定理获得后验分布，并基于后验分布对未知量进行估计。Bayes估计由于充分利用了历史信息，扩大了信息源，并且基于后验分布比较容易实现点估计和区间估计。主要缺点是先验分布的选取较困难。在信息量较少时，多会采用专家经验或者工程经验给出先验分布，分布的主观性太强，容易导致后验分布估计效果较差。

到底选用何种方法进行寿命分布类型部件的参数估计并用于装备MTBF参数的评价，有何适用范围，则需要结合舰船装备维修保障数据实际情况详细分析。本文在已知寿命分布类型的情况下，比较了采用两种方法对舰船电子元器件装备寿命分布参数进行估计的结果，并分析了舰船电子元器件装备的MTBF参数值。

2 指数分布型部件的参数估计

舰船电子元器件类装备的寿命一般服从指数分布。指数型部件的寿命分布拟合检验方法主要有χ2拟合检验及F拟合检验方法[7-8]。通过收集某电子元器件维修保障数据，确定该电子元器件的寿命服从指数分布。

指数分布寿命T的失效分布函数一般表示为：

F(t)=1-e-λt,λ>0,t≥0

(1)

可以称T服从参数为λ的指数分布，其失效密度函数为：

f(t)=λe-λt,λ>0,t>0

(2)

下面讨论指数分布型部件的极大似然与Bayes参数估计的使用情况。

2.1 极大似然估计

当对n个装备进行试验，直至全部失效，假设装备每次的失效前时间为t1,t2,…,tn，则失效时间可用于表示这个装备的寿命，如果假设装备的寿命是独立且同分布的，若数据无删失，则指数分布失效密度函数的似然函数表达式可写为：

(3)

数学上，为了更好地处理逼近于零的问题，可利用自然对数转换为负对数似然函数[9]，有：

(4)

即：

(5)

若想L取最小值，令：

(6)

得：

(7)

则：

(8)

因此，指数分布参数的极大似然估计可以用平均失效前时间的倒数表示。

2.2 Bayes估计

Bayes估计一般可按如下步骤进行：

步骤1当随机变量参数θ取某个给定值时，记总体的条件概率函数为p(x|θ)。

步骤2通过参数θ的先验信息确定先验分布π(θ)。

步骤3假设X=(x1,x2,…,xn)是从先验分布π(θ)产生的θ条件下的装备失效前时间的一个样本，则样本X=(x1,x2,…,xn)的联合条件概率函数为：

(9)

步骤4由于θ是通过先验分布π(θ)产生的，可以通过考虑θ的其他值对π(θ)综合先验信息，从而得到样本X和参数θ的联合分布为：

h(X,θ)=p(X|θ)π(θ)

(10)

步骤5在样本观测值X=(x1,x2,…,xn)的条件下，依据h(X,θ)对未知参数θ进行推断，将h(X,θ)分解为：

h(X,θ)=π(θ|X)m(X)

(11)

式(11)中，m(X)是X的边际概率函数；

(12)

式(12)与θ无关，因此仅用条件分布π(θ|X)就可以对θ进行推断，计算公式为：

(13)

式(13)称为θ的后验分布。

步骤6在平方损失函数下，θ的Bayes估计即为后验分布π(θ|X)均值[10]。

对于指数分布型装备，其参数λ的共轭先验分布为gamma 分布Ga(a,b)[11]，参数λ的先验分布的核为：

π(λ)∝λa-1exp(-bλ)

(14)

式(14)中，a、b为超参数。

对于指数型部件来说，理论失效率λ0满足：

(15)

当先验分布确定参数λ后，其数学期望E与MTBF关系为：

(16)

从而有：

a=b/MTBF

(17)

为了获得超参数(a,b)的关系式，可以将工作失效率λ的熵最大化考虑。λ的熵为：

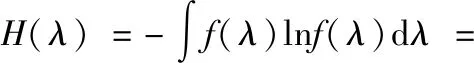
(18)

当a=1时，λ的熵H(λ)可以得到最大值。此时，将a的值a0=1代入式(17)，得到b的值b0=MTBF。

通过确定超参数a、b的值，便可以得到参数λ先验分布的核为：

π(λ)∝λa0-1exp(-b0λ)

(19)

一般情况下，在装备使用过程中，可以收集到n个部件一段时间τ内的故障时刻ti(i=1,2,…,r)，因此可以将收集到的故障数据看为定时截尾数据，即：

t1≤t2≤t3≤…≤tr≤τ(r≤n)

(20)

联合条件概率函数为：

(21)

h(t,λ)=P(t|λ)π(λ)∝λr+a0-1exp(-λTa-λb0)

(22)

根据Bayes估计后验分布的计算公式，参数λ后验分布的核可表示为：

π(λ|t)∝λr+a0-1exp(-λTa-λb0)

(23)

参数λ的后验均值满足：

(24)

式(24)中，c是和λ无关的常数。通过式(24)便可以得到参数λ的Bayes估计。

3 算例分析

为验证以上两种方法在指数分布型部件参数估计中的实际使用情况，通过以下算例进行研究。

通过收集某电子元器件维修保障数据，确定该电子元器件的寿命服从指数分布。其理论失效率λ0=180×10-6h，理论MTBF=5 000 h，任务时间T=1 000 h。现有10个相同元器件同时工作，至任务结束，有1个部件失效，失效时刻t为57 h，部件工作时间如表1所示。

表1 部件工作时间

通过前面的计算方法，可以得到该电子元器件参数λ的极大似然估计和Bayes估计值分别为110.5×10-6和 142.3×10-6。两种参数估计方法计算得到的估计值和标准值对应的装备失效前时间的失效概率密度函数曲线如图1所示。

图1 两种估计方法在指数分布中计算得到的失效概率密度函数曲线

由图1可以发现，在只有1个失效数据的情况下，Bayes估计的结果值与标准值更为接近，也可以说此时Bayes估计具有更好的适用性。

通过增加任务时间来增加失效数据，观察两种方法的估计值与标准值的偏差，如表2所示。

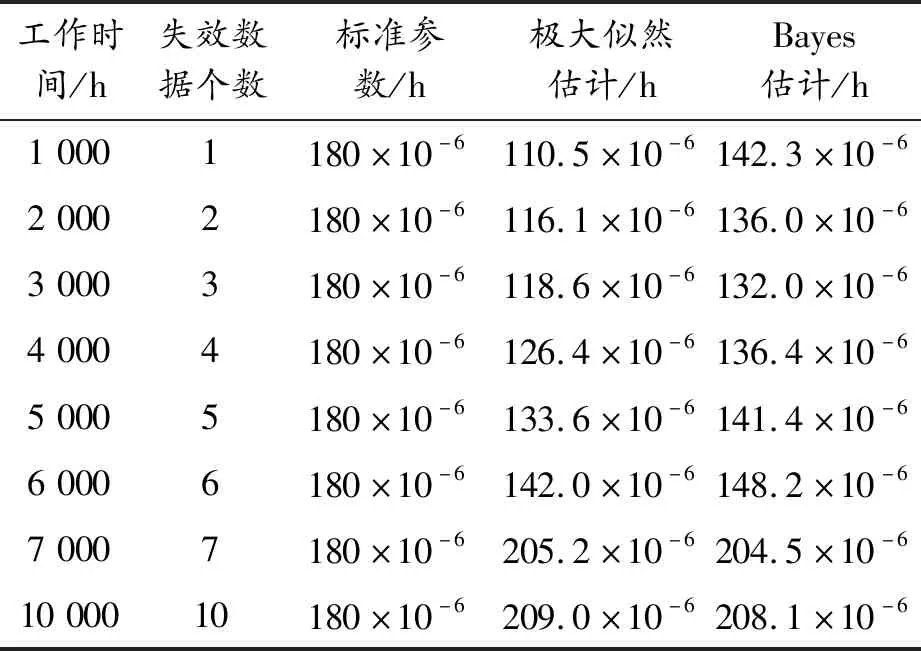
表2 两种估计方法计算结果与标准值

可以发现，在实际MTBF与理论MTBF较接近的情况下，随着任务时间的增加，极大似然估计和Bayes估计计算的结果与标准参数值都比较接近，但Bayes估计始终比极大似然估计得到的参数值要更加接近于标准参数值。当任务时间增加至7 000 h后，此时该电子元器件的失效数据个数为7，极大似然估计和Bayes估计的计算结果相差很小，且都很接近于标准参数值。通过对多个同类电子元器件采用同样方法并求均值发现： MTBF实际值与标准值比值约等于0.7时，为两种方法的适用临界点，即可通过此临界点判断哪种方法更适用。

4 结论

在对指数分布型部件进行参数估计时，Bayes估计具有更高的准确性、更强的适用性。由于Bayes估计的计算依赖于先验信息的MTBF值，因此装备说明书提供的MTBF理论值的准确程度对Bayes估计结果的影响很大，通过大量计算发现，当MTBF实际值与标准值比值小于0.7左右时，就会出现极大似然估计优于Bayes估计计算结果的情况。那么，在实际计算过程中，当出现极大似然估计计算结果优于Bayes估计结果时，也可以间接说明装备实际MTBF值与理论MTBF值存在较大偏差，可以用于评价装备的实际MTBF是否符合指标要求。