高速射弹入水过程弹道与流体动力特性研究

郝 博，代 浩，吕 超

(1.东北大学 机械工程与自动化学院， 沈阳 110819；2.东北大学秦皇岛分校控制工程学院，河北 秦皇岛 066004)

高速射弹入水过程涉及到空化、湍动、穿越自由液面等复杂的物理现象[1]。射弹在入水过程中会形成空泡，空泡的发展过程会影响到射弹的弹道及其流体动力特性。而且入水问题的应用领域十分广泛，例如超空泡射弹、空投鱼雷、深水炸弹的硏发，因此对高速射弹入水问题展开深入的研究至关重要。

国内外学者从不同角度对射弹的入水问题进行了分析和研究。M.Lee等[2]利用能量守恒原理对高速射弹入水空泡发展的过程进行了研究；T.Milo[3]对球体撞击水面的流动分布、载荷特性等问题进行了研究，得到了球体入水过程的阻力系数；R.Cointe等[4]提出了运动体冲击水面时的气垫效应，一些学者通过应用实验和理论证明了这一效应的存在；S.Gaudet[5]研究了空泡闭合时雷诺数对阻力的影响；A.May[6]开展了运动体垂直入水研究，分析了运动体速度、头部形状对入水空泡形成、发展过程及闭合特性的影响；王瑞琦等[7]开展了不同头型弹丸低速垂直入水实验的研究，分析了弹丸的入水空泡形态和空泡的闭合；朱珠等[8]对旋转射弹高速倾斜入水多相流场与弹道进行了数值模拟；肖海燕等[9]研究高速射弹小角度入水过程中的空化现象和弹体运动规律；路丽睿等[10]研究射弹头型对低速倾斜入水空泡及弹道特性的影响；马庆鹏[11]对高速射弹入水过程空泡形态发展规律、弹道特性及流体动力特性进行了系统深入的研究；方城林等[12]研究了不同射弹头型对高速射弹垂直入水的流体动力和流场特性的影响；黄鸿鑫等[13]研究了射弹的头部形状和质心位置对髙速入水稳定性的影响；张伟等[14]进行了速度在35～160 m/s的平头、卵形和截卵形弹体入水实验，分析了弹体头部形状对入水弹道稳定性的影响。

目前，低速入水问题的研究较为深入，高速入水的研究依然是一个较新的方向，特别是高速射弹入水过程弹道与流体动力特性的研究较少。本文以FLUENT软件为计算平台，采用重叠网格技术与6DOF动网格对高速射弹入水过程进行数值模拟研究，分析了不同结构射弹入水过程空泡形态、弹道稳定特性和流体动力特性的变化规律。

1 数学模型和数值计算

1.1 流体控制方程

本研究采用VOF模型描述高速射弹入水的过程，由气、汽、液三相形成的各相流动，从而建立该问题的控制方程。VOF模型将多相流体看作为密度可变的单相介质，各相流体具有相同的速度、压力流场参数，通过计算可以得到各相流体所占的体积分数，它们的体积分数满足如下关系式:

αl+αg+αv=1

(1)

式(1)中，αl、αg、αv分别为水相、气相和水蒸汽相的体积分数。

混合相的连续性方程为：

(2)

式(2)中:ui为速度分量，i=1,2,3;xi为坐标分量，i=1,2,3;ρm为混合相的密度。ρm的表达式为：

ρm=αlρl+αgρg+αvρv

(3)

动量守恒方程为：

(4)

式(4)中：μt=ρmCμk2/ε为湍流粘性系数；μm为混合介质的动力粘性系数。μm的表达式为：

μm=αlμl+αgμg+αvμv

(5)

在射弹高速入水时，将产生随机性较强的湍流，本研究采用k-ωSST湍流模型来模拟入水过程中的湍流现象，该模型具有较高的精度和可信度，其输运方程为:

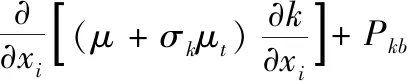
(6)

(7)

其中，湍流动力黏度的控制方程为：

(8)

(9)

(10)

式(10)中:d为流场中质点距离最近壁面的距离；ν为流体的运动黏度。

射弹入水的过程将发生空化，本研究采用 Schnerr and Sauer 空化模型对空化现象进行模拟，其控制方程为:

(11)

式(11)中:Fvap=50和Fcond=0.001为经验常数；RB=1×10-6m为空化气核半径;αnuc=5×10-4为不可凝结气体的体积分数。

1.2 计算模型

针对不同形状弹体的入水问题，本文进行了入水角为90°情况下的高速入水数值模拟研究。射弹分别采用锥形平头、椭圆平头和锥形锥头等3种实心结构，其几何结构如图1 (a)、图1 (b) 和图1 (c) 所示。其中，弹体材料为钨合金，密度为ρ=17.5 g/cm3。

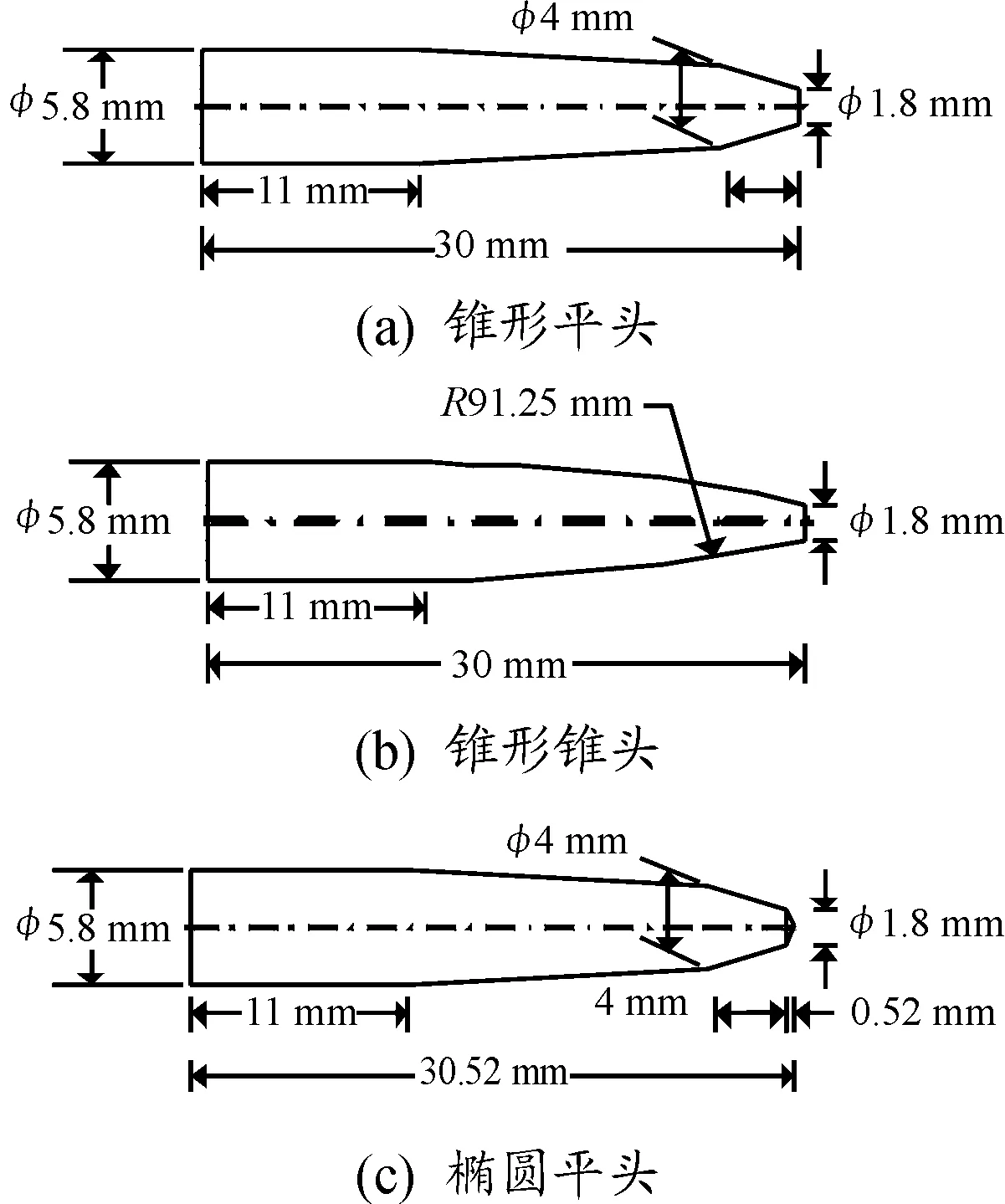
图1 不同结构射弹示意图

1.3 计算域及边界条件

为了研究射弹高速倾斜入水运动过程的弹道特性与流体动力特性，本文数值模拟采用三维模型。图2展示了计算域z=0平面的截图以及边界条件，其计算域长度为1.5 m、宽度为1.5 m、高度为3 m，空气域高度为0.6 m，水域深度为2.4 m，重力沿y轴负方向。初始时刻弹体轴线与自由液面的夹角为90°，弹体初速度为800 m/s，弹体初始质心位置位于(0,0,0)处。计算域顶端为压力入口，压强为大气压，底端为压力出口，出口压力为2.4 m水深的静水压强，计算域x+和x-面为滑移壁面，z+和z-面为symmetry边界条件，射弹表面为壁面条件。

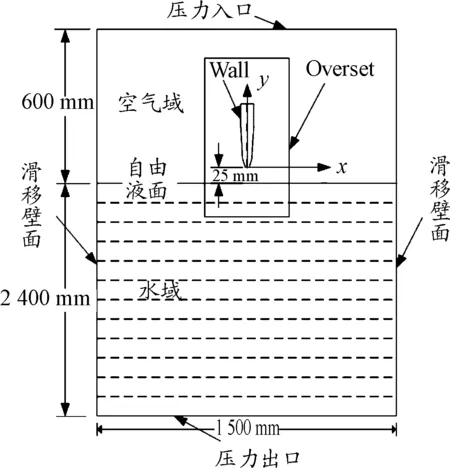
图2 计算域及边界条件示意图

1.4 重叠网格

目前对于运动体的数值模拟多采用动网格技术，但是动网格在网格重构的过程中会发生较大的变形，从而导致网格的质量低于初始值，模拟结果精度差。重叠网格技术是采用多套网格，将需要计算的复杂流体区域分成具有简单规则的计算子区域，每个计算子区域中的网格是单独划分的，各个子区域之间存在着不同程度的重叠关系[15]。

重叠网格技术与6DOF动网格相结合可以消除动网格技术中网格重构更新时网格质量变差的结果，因此，重叠网格在网格运动期间始终可以保持很高的网格质量，同时具有强大的模拟复杂运动的能力。当重叠网格与6DOF网格运动结合时，一般采用两套网格：一套为流体计算域的背景网格，另一套为包裹被分析物体的前景网格。在计算对象运动的过程中，通过计算软件持续的实时检査背景网格和前景网格的重叠区域，在重叠区域通过建立插值关系来实现流场信息的交换，从而达到整体的求解[16]。本文的背景网格区域是1.2节中的长方体计算域，前景网格区域是一个包裹射弹的圆柱形计算域，在射弹运动过程中，前景网格区域随射弹同步运动，其中涉及到前景网格和背景网格的挖洞嵌套操作，图3为射弹初始时刻进行挖补操作之后的网格在z=0平面上分布。

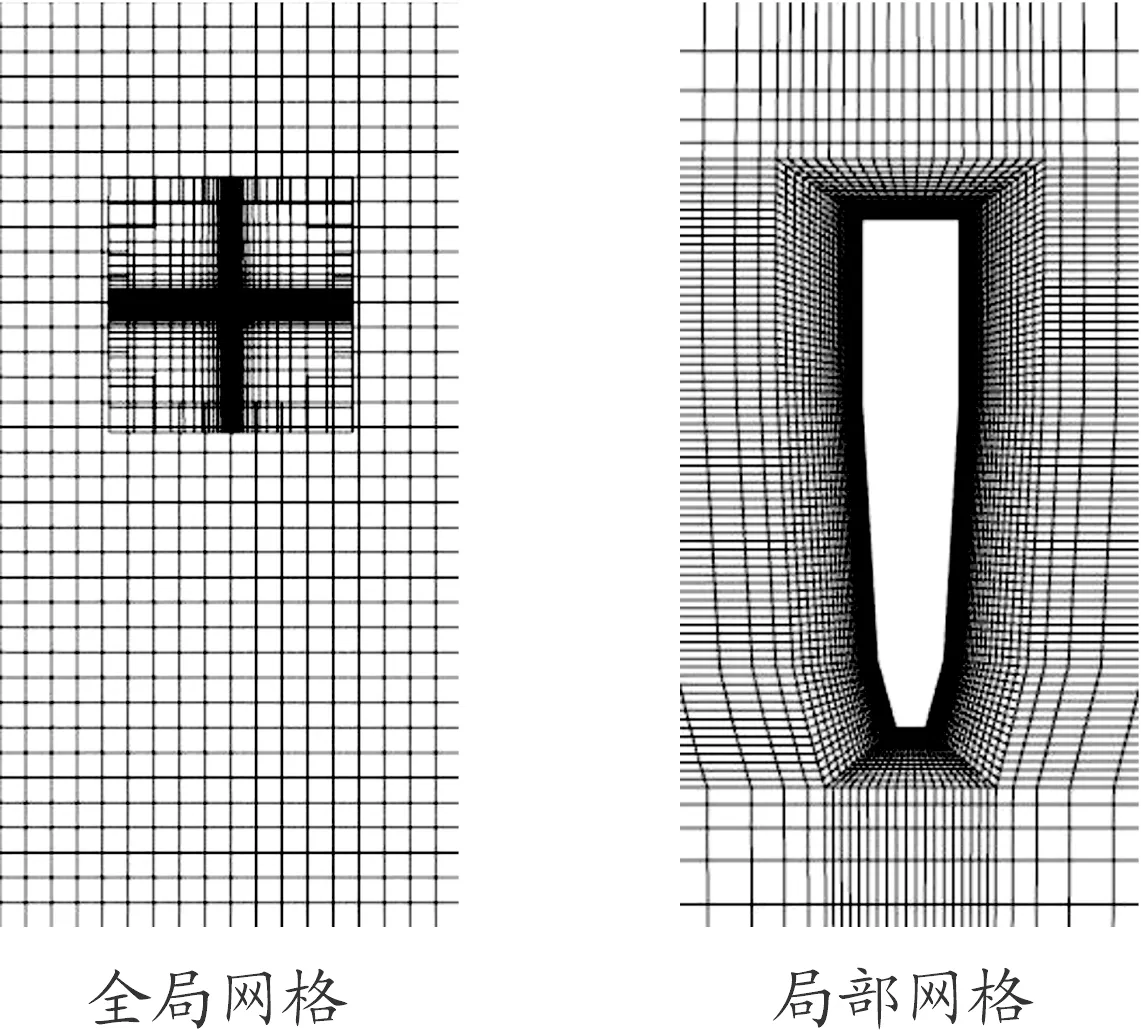
图3 初始时刻在z=0平面网格示意图

本文对流体控制方程在时间和空间上的离散方法选用基于VOF多相流模型的有限体积法，其中速度场和压力场的耦合求解采用 Coupled算法，压力场的空间离散选用 PRESTO格式，耗散项、湍流和动量方程均采用了二阶迎风格式。

2 数值方法验证

对锥头圆柱体射弹垂直入水问题进行数值模拟计算,实验选用θ=90°的锥头圆柱，长度为50 mm，柱体直径为10 mm，材料密度为ρ=2.7 g/cm3，初始入水速度为500 m/s，计算采用重叠网格技术，分别计算了入水后射弹速度和深度随时间的变化。将数值计算结果与文献[11]结果进行对比，可以看出，仿真结果和文献[11]中实验数据的曲线几乎一致，从而说明本文数值计算的可靠性。由图4可以得到，射弹入水后速度下降非常快，时间不足1.5 ms，速度从500 m/s下降至200 m/s，速度下降的幅度随着时间不断增加而逐渐平缓，同时随时间不断增加，入水深度H増加的幅度逐渐缓慢。这一结果表明，射弹在入水初期受到阻力非常大，随着速度不断衰减，所受的阻力也在减小。通过以上分析，可以看出本文使用的方法能够较好地模拟高速射弹入水过程的动力学特性。

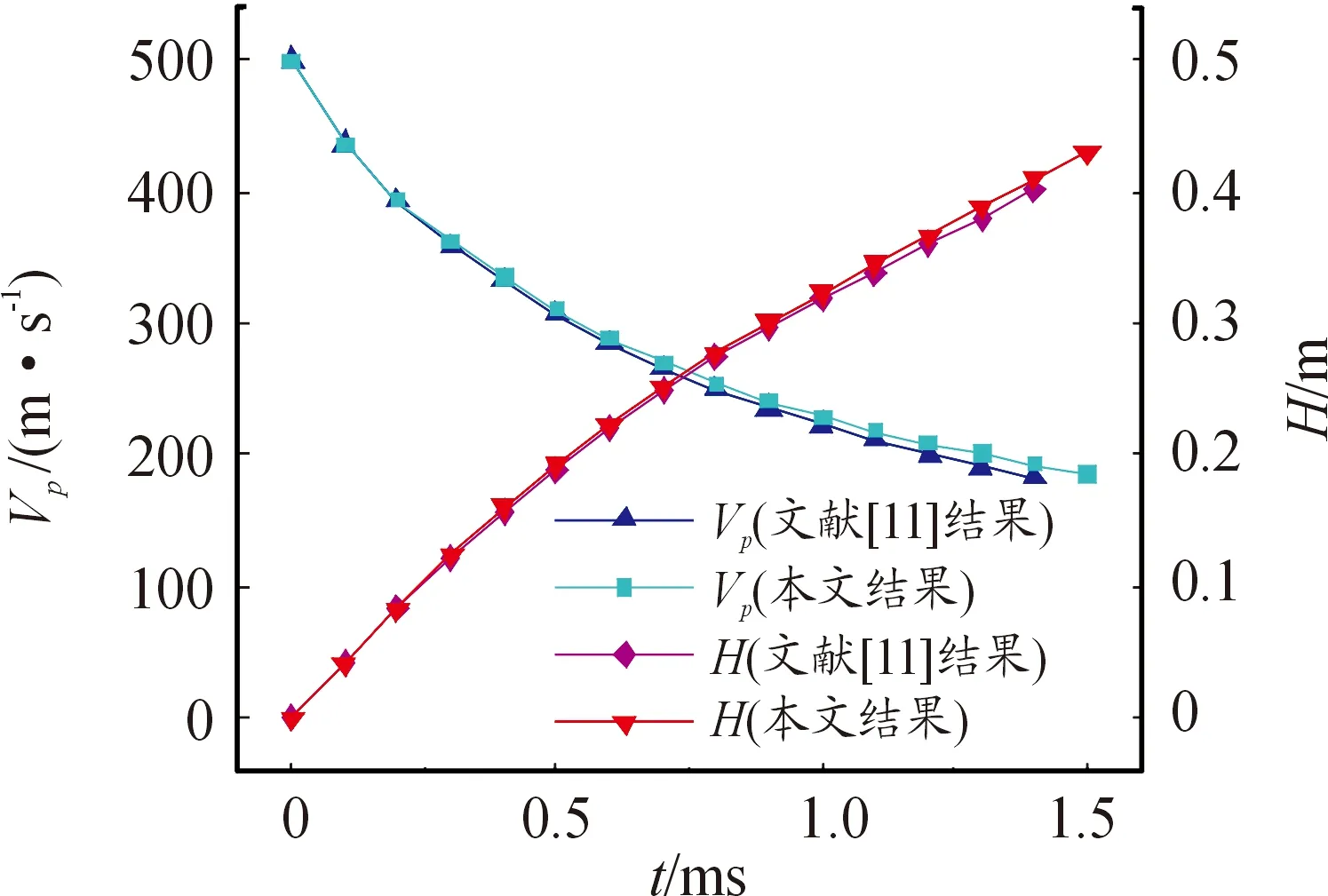
图4 入水速度和入水深度变化曲线

3 计算结果与分析

通过数值计算，在射弹初速度为800 m/s，入水角度为90°情形下，对超空泡形态、弹道稳定特性和流体动力特性进行了分析。

3.1 空泡形态特性

射弹入水过程经历入水撞击、空泡形成和开空泡等阶段。为了更好地观察空泡形态变化，图5给出了不同结构射弹入水空泡形态变化过程。在射弹入水以后，水中会形成一个完全包裹射弹的超空泡，随着入水过程的持续进行，空泡会被拉长，直径会先增大后缩小，而且空泡尾部在水压的作用下迅速消失，随着射弹姿态的剧烈变化，空泡的形态变得越来越不对称。由此可以得出，不同射弹在入水初期具有较好的姿态，但随着入水深度的不断增加，锥形平头射弹姿态变化不大，椭圆平头射弹姿态发生一定程度的偏转，而锥形锥头射弹的姿态发生了较大偏转，这是由于射弹下表面沾湿，射弹的稳定性逐渐变弱。

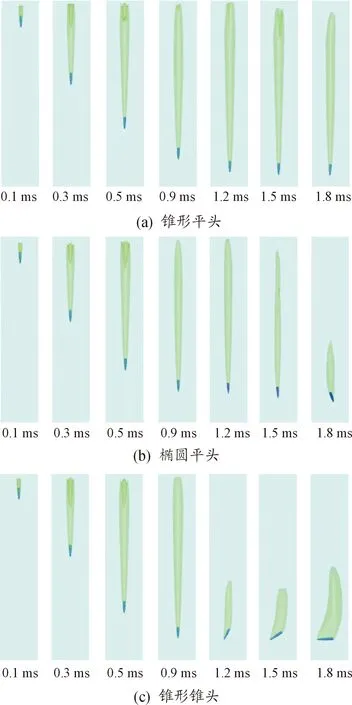
图5 射弹入水空泡形态变化过程

3.2 弹道特性分析

图6为3种不同结构射弹质心的运动轨迹，由图6(a)知，在射弹未进入水中时，其质心运动轨迹基本保持直线，射弹在接触水面后轨迹逐渐发生偏离，这是因为射弹入水后带空泡航行过程中，作用在射弹头部上的流体动力可简化分为轴向力和法向力，前者引起弹体的速度衰减，后者产生一个围绕射弹质心的力矩，导致射弹产生俯仰角速度，从而使射弹轨迹发生偏离，随着弹体下表面与水接触面积增加，射弹轨迹严重偏移，从而使得入水弹道出现了不稳定现象。同时可以看出，锥形平头射弹在水中具有良好的弹道稳定性，椭圆平头射弹往往由于受力不均衡在入水后期发生偏转，锥形锥头射弹则在入水前期即发生偏转。由图6(b)和图6(c)知，在初始没有x方向和z方向速度的情形下，射弹产生了x方向和z方向的偏移，这是因为射弹撞击水面时只有头部与水接触，且沾湿面积小，射弹受到水下的微小扰动和不稳定的流体动力，在射弹沾湿面积越大，x方向和z方向的偏转变化越大。

图6 射弹质心的运动轨迹

图7为不同结构射弹运动过程中x、y、z方向的速度随时间变化曲线，在射弹未进入水中，各个方向上的速度基本不变。由图7(a)和图7(c)可知，在射弹入水初期，x方向和z方向的速度几乎为零，当射弹沾湿面积增大时，x方向和z方向的速度缓慢增大，且量级非常大。这是由于射弹失稳沾湿时，形成了x方向和z方向的分力，从而导致x方向和z方向速度不断增加。再通过图7(b)可以看岀，在射弹入水初期同一时刻，y方向速度随锥形锥头射弹、椭圆平头射弹、锥形平头射弹的次序递减，这是因为射弹受到的重力几乎一样，而阻力不一样造成的，阻力越大，射弹y方向速度衰减越快；入水后期，锥形锥头射弹y方向速度急剧减小，其次为椭圆平头射弹，锥形平头射弹y方向速度急剧减小现象不明显，这是由于锥形锥头射弹稳定性最差，射弹侧表面沾湿变大，从而导致y方向速度急剧减小。

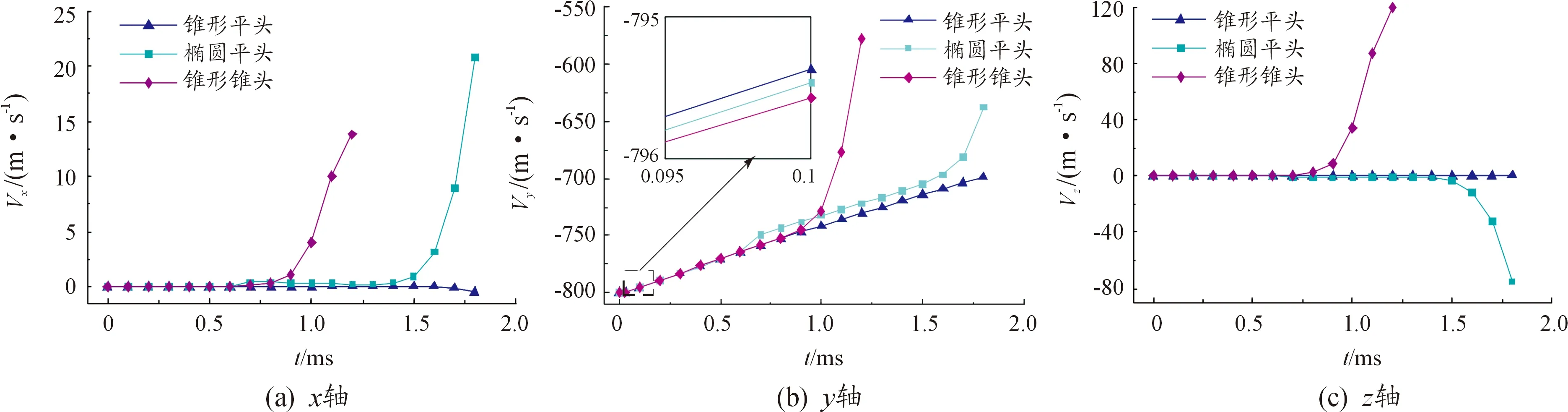
图7 射弹各方向上的速度变化曲线

3.3 流体动力特性

图8为不同结构射弹在入水过程中阻力系数随时间变化曲线，从图8可以看出，射弹在空气中运动时，阻力系数非常小，当射弹头部与水面接触，阻力系数瞬间增大，产生一个峰值，这是因为射弹外围流体介质由密度较小的空气转为密度较大的水，然后阻力系数逐渐减小，在超空泡还未完全形成的时候，射弹部分与水接触，存在较大的摩擦阻力，随着超空泡的不断变大并将射弹包裹，仅头部与水接触，在这个过程里摩擦阻力逐渐减小。在射弹入水一段时间以后，阻力系数迅速增大，因为此时射弹下表面与水接触，导致射弹受力急剧增大。同时可以观察到，射弹头部触水后，阻力系数峰值按锥形平头射弹、椭圆平头射弹、锥形锥头射弹的次序递减，这是由于锥形平头射弹头部液体的流动方向更接近轴向，不易向径向流动，因此产生较大阻力。在进入稳定流动阶段后，阻力系数稳定值按锥形锥头射弹、椭圆平头射弹、锥形平头射弹的次序递增，因为锥形锥头射弹气流可以平滑地流过，压强不会急剧升高，所以压差阻力较小。

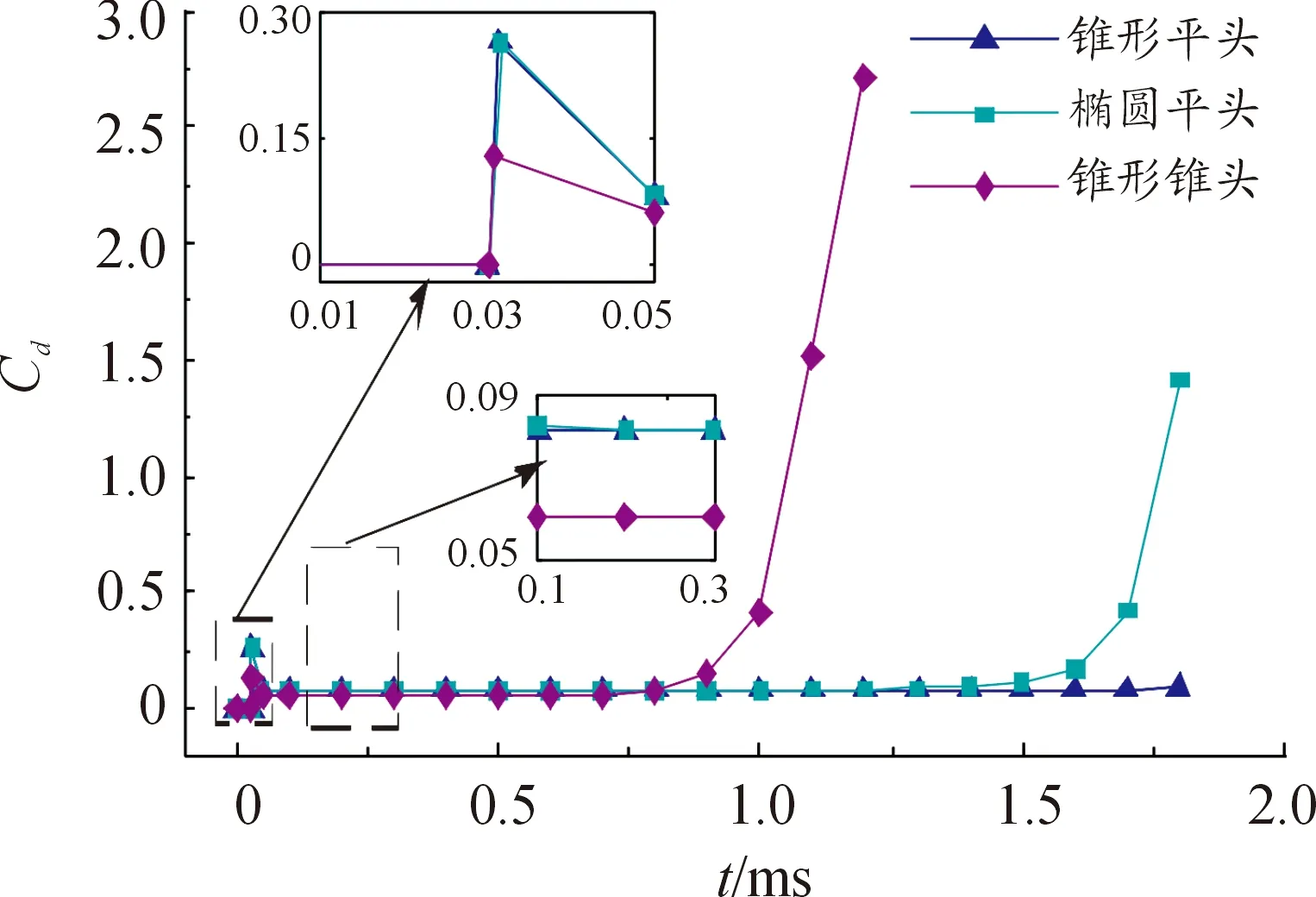
图8 射弹入水过程阻力系数变化曲线

图9为不同结构射弹入水过程射弹头部最大压强随时间变化曲线。从图9可以看出，在入水之前，射弹头部最大压强近似为0，撞击自由液面阶段由于冲击作用，射弹头部最大压强值要远大于其他任何时刻，并且出现峰值，其值按锥形平头射弹、椭圆平头射弹、锥形锥头射弹的次序递减，但压强峰值脉宽基本相同。随着入水深度的增加，压强最大值逐渐下降，最后趋于平缓，在相同时刻，其数值按锥形锥头射弹、椭圆平头射弹、锥形平头射弹的次序递减，这是因为在同一入水时刻下，锥形锥头射弹受到的阻力较小，瞬时速度较高，头部也相应承受更大的压强。

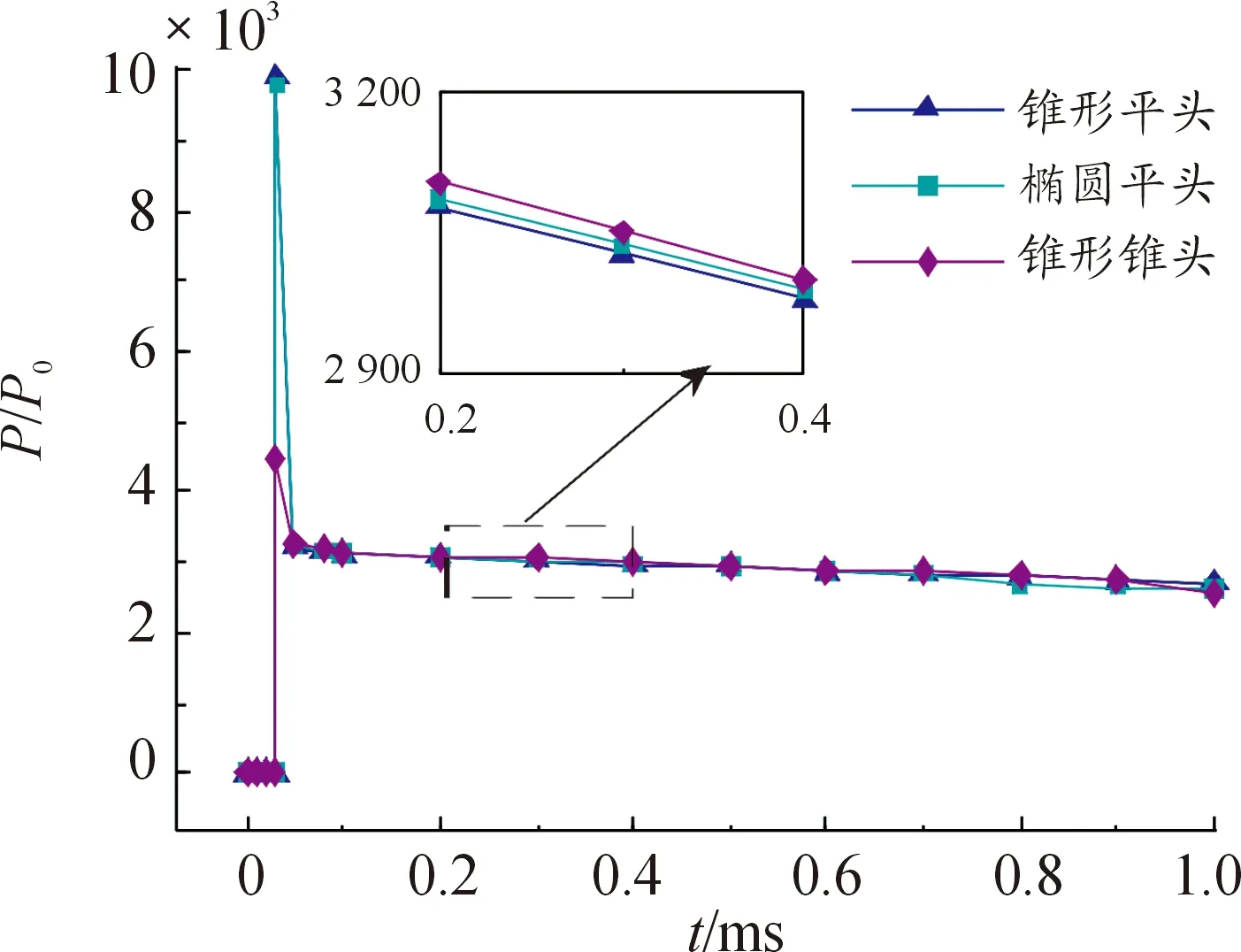
图9 射弹头部最大压强变化曲线

4 结论

1) 在射弹入水初期，水中形成一个完全包裹射弹的超空泡，随着入水深度增加，空泡被拉长，直径先增大后缩小。射弹下表面沾湿以后，空泡形态和射弹姿态变化明显。

2) 射弹形状对射弹入水的弹道稳定性影响很大，锥形平头射弹最稳定，其次是椭圆平头射弹，锥形锥头射弹最差，为提高射弹入水稳定性应选用锥形平头射弹进行设计。

3) 射弹撞水阶段，阻力系数瞬间增大，产生峰值，随后趋于平稳，当射弹下表面与水接触时，阻力系数迅速增大。

4) 由于冲击作用射弹撞水阶段，射弹头部最大压强值要远大于其他时刻，其峰值按锥形平头射弹、椭圆平头射弹、锥形锥头射弹的次序递减，但压强峰值脉宽基本相同。