某型水下拖曳设备水动力仿真研究

2021-01-12周陈颖赵昌方仲健林

兵器装备工程学报 2020年12期

周陈颖，任杰，张哲，赵昌方，仲健林

(1.南京理工大学机械工程学院，南京 210094； 2.中国船舶工业集团公司第七〇八研究所，上海 200011)

我国海域幅员辽阔，拥有丰富的海洋资源。随着人类科技的进步，对海洋的探索及应用也有了新的发展。水下拖曳系统在海洋资源勘测、海底地貌观察、渔业、军事等都有着广泛的应用。由于流体具有一定的粘滞性，水下拖曳设备在前进过程中会受到流水阻力、水升力、水侧向力及水下力矩等的共同作用，这类作用是决定拖曳设备前进速度及水中姿态的重要因素[1-3]。因此开展水下拖曳设备的水动力研究具有重要的理论意义及工程实用价值。水下拖曳系统水动力特性的研究也颇受学者们关注，孙晔等[4]发现重心位置与运动姿态有关，俯仰角为40°时呈现较好的深度调节运动姿态；孙昕煜等[5]计算流阻力系数并与试验数据进行对比，证明采用CFX 软件对拖曳链进行水动力分析是有效可行的；Azarsina等[6]进行纯偏航或之字形拖曳试验，发现摇摆-偏航耦合产生振幅可达6倍直径，最大偏航角约为15°。由于受到水流的影响，不同工况下水下拖曳设备的水动力特性是复杂多变的，因此研究不同航速及姿态角同时作用下的水动力特性具有很好的应用前景，关于水动力特性与各运动参数间理论关系的研究较少。

本文主要以某型水下拖曳设备为研究对象，通过数值计算分析水下拖曳设备在不同侧摆及升降状态下，以及不同航行偏摆角度下的水动力特性，并根据仿真结果利用插值与拟合方法揭示水动力特性与水下拖曳设备航速及姿态角的理论关系。

1 数值理论

1.1 流体力学控制方程

在三维直角坐标系中，流体的速度矢量U在3个坐标上的分量分别为u、v、w，流体的密度为ρ，考虑非定常流动。建立包括质量、动量及能量守恒方程的流体力学控制方程[11-13]。

质量守恒方程：

(1)

动量守恒方程：

(2)

能量守恒方程：

(3)

式(3)中：Cp为比热容；T为温度；k为流体的传热系数；ST为粘性耗散项。

1.2 离散化及压力修正方法

流体力学的控制方程理论上存在真解，但是由于复杂的边界条件、强烈的非线性及各方程之间的耦合，使得真解的获得极其困难甚至不可能。有限体积法是一种常用的离散化方法，在CFD领域获得了广泛应用，本文采用该方法进行流体数值研究。流场数值计算是将计算域离散成多个体积单元，并对每个体积单元的控制方程组进行求解，一般分为分离解法和耦合解法，其中分离解法具有更快的求解速度。本计算采用的是分离求解算法中的半隐式算法-SIMPLE算法，其核心是采用“预测-修正”的过程在交错网格的基础上来计算压力场，求解Navier-Stokes方程。

2 数值方法验证

2.1 计算模型

考虑扑翼在无界流中为刚性体，其运动坐标系及中心点定义如图1所示。采用动网格技术对扑翼的运动过程进行动态计算，为提高计算精度对扑翼近壁面处网格进行加密处理，壁面附近网格尺度约为2.6 mm；同时为保证动网格更新后的质量，采用交界面以区分不同的流场。

图1 扑翼运动坐标系及中心点示意图

2.2 计算结果

图2为扑翼在典型周期内的推力系数曲线，扑翼运动流场的速度分布云图如图3所示。

图2 不同运动中心的推力系数曲线

图3 扑翼运动流场速度分布云图

由图3可知扑翼前沿涡与尾部涡流的生成及运动是扑翼产生推力的主要原因。

2.3 对比验证

为了验证本计算方法的可行性与准确性，与文献[14]所得到的计算数据进行对比，计算工况参数如表1所示。

表1 计算工况参数

扑翼在运动时，将以某一点为运动中心进行翻转运动，不同运动中心位置将对扑翼的水动力特性产生影响。表2、表3为不同运动中心的扑翼推力系数。

表2 扑翼推力系数峰值

表3 扑翼平均推力系数

由表3可知，推力系数峰值相对误差较小且在允许范围内，当xoc=0.25、xoc=0.75时，平均推力系数的相对误差较大，原因是数值模型与计算步长稍有不同，但整体二者的变化趋势是吻合的。随着运动中心的右移，扑翼做翻转运动的角度幅值虽然恒定，但扑翼前沿的运动幅值却在减小，导致其所受推力不断降低。采用的数值计算方法在计算水动力方面的精度满足工程应用的要求。

3 结果及讨论

3.1 计算模型

水下拖曳设备计算模型示意图如图4所示。

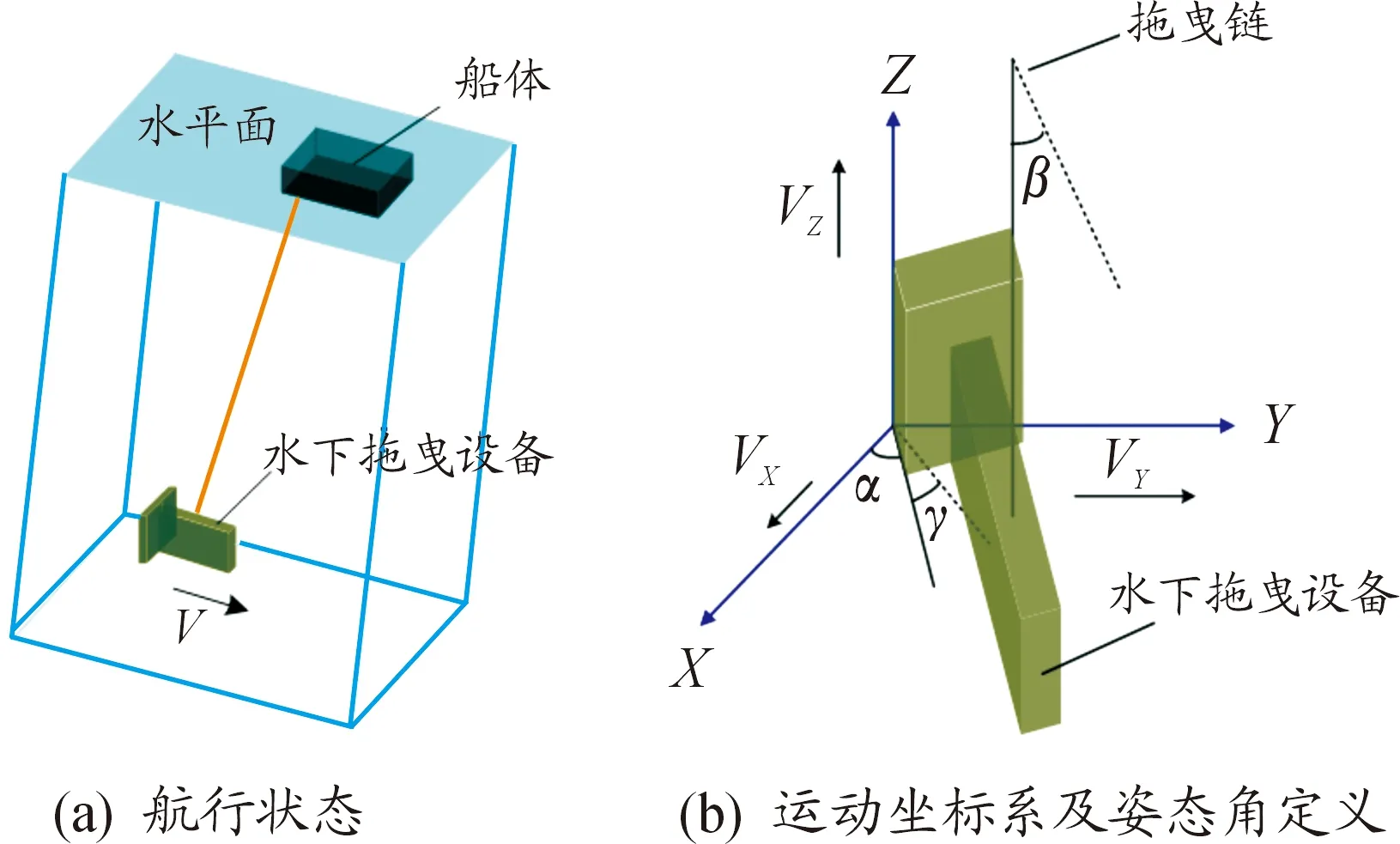
图4 水下拖曳设备计算模型示意图

水下拖曳系统通常由船体、拖曳链及主动或者被动的拖曳设备组成，通常用于探测的拖曳系统可以在拖曳设备上搭载各种探测器，如声呐、摄像头等。在船体前进过程中，由拖曳链拖动设备在水中运动，拖曳设备的航速和姿态角可以通过拖船速度和收放拖曳链等来控制，拖曳设备的航行原理及基本外形如图4(a) 所示，其中V为水下拖曳设备航速。由于受到外界流体环境的影响，水下拖曳设备的运动具有多个自由度，图4(b)中各运动参数的定义如下：X向为水下拖曳设备前进方向，Y向为侧向，Z向为升沉方向；Vx为前进速度，Vy为侧向速度，Vz为升沉速度；α为偏摆角，β为侧摆角；γ为俯仰角。

3.2 结果分析

Drag/N代表水下拖曳设备所受的阻力，Lift/N代表水下拖曳设备所受的升力；Drag-Fx/ N、Drag-Fy/ N分别代表x和y方向所受的阻力；Momentum-Mx/ (N·m)、Momentum-My/ (N·m)、Momentum-Mz/ (N·m)分别代表绕x、y、z方向的力矩，横坐标Velocity/Kn代表航速。

1) 水下拖曳设备在无侧摆无升降航行状态下所受阻力随航速的关系曲线如图5、图6所示。

图5 不同偏摆状态下阻力随航速的变化关系曲线

图6 不同偏摆状态下升力随航速的变化关系曲线

2) 水下拖曳设备在有侧摆无升降状态下所受阻力、力矩随航速的关系曲线如图7～图9所示。

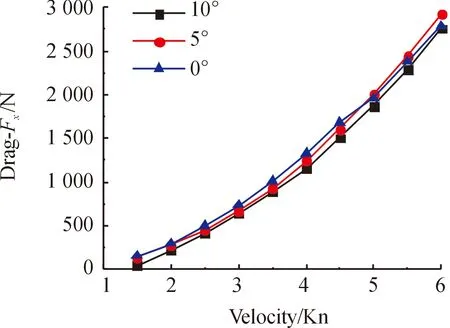
图7 不同侧向速度下阻力( Fx)随航速的变化关系曲线

图8 不同侧向速度下阻力(Fy)随航速的变化关系曲线

图9 不同侧向速度下力矩(Mz) 随航速的变化关系曲线

由图7可知，在有侧摆无升降状态下，阻力Fx随航速的3条变化曲线相互交叉，在航速一定的情况下，侧向速度Vy对阻力Fx的影响并没有出现明显的规律。由图9可知，力矩Mz总体呈现统一的趋势，然而在不同侧向速度下，Mz随航速变化的趋势也不相同，当Vy= 0.3 m/s时，Mz随航速的变化曲线为“S”形，即存在一个拐点，假设该点的航速为“拐点航速(Vg) ”。当航速VVg时，Mz随Vy的变化率逐渐减小。

3) 水下拖曳设备在绕Z轴的不同扭转状态下所受力矩随航速的关系曲线如图10～图12所示。

图10 绕Z 轴扭转5°状态下所受力矩随航速的变化关系曲线

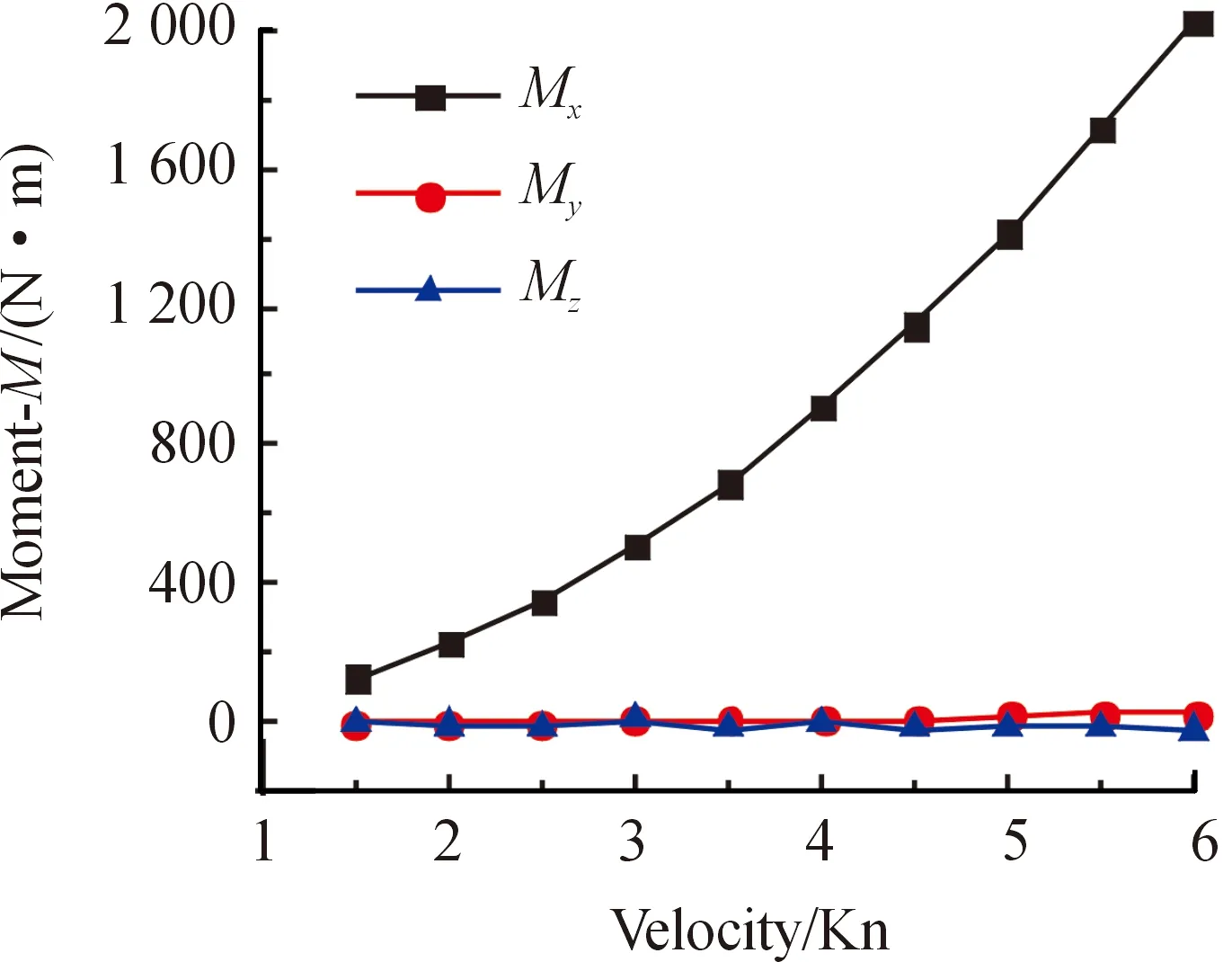
图11 绕Z轴扭转10°状态下所受力矩随航速的变化关系曲线

图12 绕Z轴扭转15°状态下所受力矩随航速的变化关系曲线

由图10～图12可知，在相同绕Z轴扭转角度下，Mx的大小及变化率都远高于My及Mz，说明当拖曳设备存在绕Z轴扭转时，X方向更容易出现翻转产生波动，且航速越大，不稳定性越剧烈。当扭转角度由10°增加到15°时，Mx未出现较大增幅；然而当扭转角度降为5°时，Mx降幅较大，航速为6 Kn时不同扭转角对应的Mx值之差达1 500 N·m以上。

3.3 水动力拟合计算

基于流体计算，利用ISIGHT多学科计算平台，拟合水阻力，水侧向力及水升力的近似模型，获得Fx、Fy、Fz与Vx、Vy及Vz之间的相互关系。各个方向的力矩与航行速度及位置姿态有关，建立俯仰力矩My、自转力矩Mx、偏航力矩Mz的近似模型，获得My、Mx、Mz与Vx、Vy、Vz,以及偏摆角α、侧摆角β、俯仰角γ之间的相互关系。

水阻力为：

(4)

水侧向力为：