空气捻接器凸轮过渡曲线运动特性分析

肖乾浩，杨福芹，闫纪媛，姜敬伟

(青岛科技大学机电工程学院，山东 青岛 266061)

0 引言

在工业生产中，自动络筒机已经发展成为一种集机械、电气和流体等多种学科融合的高端机械设备，具有人工依赖性小、精密程度高的特点，有力地减小了生产周期，是国家纺织行业生产水平的关键标志。国内外研究人员对自动络筒机进行了深入的研究[1-4]。目前的研究主要集中在自动络筒机的生产效率、系统设计等方面，而缺少对其零部件运动特性的分析。空气捻接器是自动络筒机的核心构件之一，通过凸轮带动连杆运动实现对纱线的剪切和接头[5]。凸轮廓线平面展开后是折回直线[6]，由于钢滚子受凸轮廓线的约束，如果在折回处没有良好的过渡曲线，很容易引起连杆的振动、冲击和噪声[7]，降低钢滚子和凸轮接触副的工作效率，甚至影响凸轮传动机构的寿命。因此，本文对不同形式的过渡曲线方程进行归纳，探究不同参数对过渡曲线的位移、类速度和类加速度的影响。

1 过渡曲线坐标系

空气捻接器内部结构如图1a所示。设惯性参考系固定在空气捻接器机架上，取凸轮转动圆周切向方向为X向，空气捻接器建立的右手动坐标系XOY如图1b所示。

图1 空气捻接器内部结构示意和凸轮动坐标系

过渡曲线沿圆柱母线展开如图2所示。过渡曲线MN与凸轮表面相切于M、N两点，且与Y轴相交于P点。P点是过渡曲线MN中点，P点的纵坐标值为hP；分别做过M、N点的切线的垂线交Y轴于一点O′；θ为凸轮过渡曲线过渡角；δ为过M点或N点的切线与捻接器凸轮基圆母线的夹角，其值为过渡角的一半；过渡曲线切点N的纵坐标值为s，s为动程。

图2 过渡曲线展开

2 过渡曲线形式

钢滚子在滚过凸轮过渡曲线时，因不同的过渡曲线而呈现不同的运动形式，通常可以分为突然折回、圆弧过渡、抛物线过渡和多项式过渡。其中，突然折回[8]是指钢滚子实现快速加速和减速、运动方向快速转变的理想情况，由于钢滚子和其连接的连杆机构不可避免地存在惯性作用，不易实现快速折回；圆弧过渡是指钢滚子在由基圆过渡至推程段或者由回程段过渡至基圆时，钢滚子滚过的轨迹展开为圆弧；抛物线过渡中，钢滚子滚入或者滚出过渡曲线两端时的运动形式为等减速运动，当到达过渡曲线中间部位时，运动形式由等加速转变为匀速运动，这种形式存在于一定数量的纺织机械等设备中，过渡曲线展开为抛物线；多项式过渡中，代数多项式可以通过增加节点和条件来拟合多种形式的曲线[9]，它的缺点在于，过高次数多项式方程因为节点划分较细、间距较小而容易导致线性方程组病态，甚至出现Runge现象[10]，同时，由于加工误差的存在和制造技术尚未完全发展，高次多项式也容易导致制造困难、提高加工成本等问题，较多应用于实际工程的是五次多项式等。

3 过渡曲线方程

冲击分为柔性冲击和刚性冲击，通过分析不同形式的过渡曲线随凸轮转角变化的位移、类速度、类加速度函数，从而确定具体的冲击形式。

3.1 圆弧过渡曲线

圆弧过渡曲线方程表示为

(1)

r为圆弧过渡曲线半径；α为凸轮转动角度；R0为凸轮半径。

类速度方程为

(2)

类加速度方程为

(3)

3.2 抛物线过渡曲线

抛物线形式的过渡曲线方程可表示为

(4)

类速度方程为

(5)

类加速度方程为

(6)

3.3 五次多项式过渡曲线[8]

将曲线MN在Y轴的右侧部分替换为五次多项式过渡曲线，可以表示为

(7)

a1、b1、c1为待定参数。

过渡曲线端点处，边界条件为

(8)

求得待定参数解为

(9)

将式(6)、式(8)、式(9)代入式(7)得Y轴右侧的五次多项式过渡曲线方程为

(10)

类速度方程为

(11)

类加速度方程为

(12)

相应地，Y轴左侧方程可以表示为

(13)

类速度方程为

(14)

类加速度方程为

(15)

4 过渡曲线运动特性探究

4.1 圆弧过渡曲线

4.1.1 凸轮半径R0对圆弧过渡曲线的影响

图3为不同凸轮半径R0对圆弧过渡曲线的影响计算结果。

图3 R0对圆弧过渡曲线的影响

由图3a可知：不同位移曲线都交于Y轴上同一点；Y轴两侧的位移值随凸轮半径R0的增大而增大，且逐渐向中间“收拢”，P点曲率半径逐渐降低。从图3b可知，同一凸轮转角α(α≠0)时，随着凸轮半径R0增大，类速度绝对值逐渐增大。从图3c可知，类加速度不为0，随着凸轮半径R0的增大，类加速度也逐渐增大，且在过渡曲线端点M、N处有最大值。当钢滚子由凸轮其他部分运动至过渡曲线端点M、N时，因类加速度不同将产生柔性冲击。

4.1.2 动程s对圆弧过渡曲线的影响

图4为不同动程s对圆弧过渡曲线的影响计算结果。

图4 s对圆弧过渡曲线的影响

如图4a所示，当动程s逐渐增大时，P点逐渐向Y轴正向移动，且P点处的曲率半径逐渐增大。从图4b可以看出：随着凸轮转角的增大，同一动程s下类速度的绝对值先减小后增大；随着动程s逐渐增加，同一凸轮转角α(α≠0)下类速度的绝对值逐渐减小；不同的曲线在凸轮转角α为0时类速度均为0。从图4c可以看出，类加速度不为0，但随着动程s逐渐增大，M点和N点处的类加速度值明显减小。

4.1.3 过渡角θ对圆弧过渡曲线的影响

图5为过渡角θ对圆弧过渡曲线的影响计算结果。

图5 θ对圆弧过渡曲线的影响

从图5a可以看出：随着过渡角θ的增加，P点逐渐向着Y轴负向移动；M、N点的位移值减小量最大，P点的位移值减小量最小；P点的曲率半径逐渐增大。从图5b可以看出：当凸轮转角α为0时，类速度值均为0；随着过渡角θ逐渐增大，同一凸轮转角α下(α≠0)类速度的绝对值逐渐减小。从图5c可以看出：类加速度受过渡角影响较为显著，随着过渡角增大，类加速度明显下降。

4.2 抛物线过渡曲线

4.2.1 凸轮半径R0对抛物线过渡曲线的影响

图6为凸轮半径R0对抛物线过渡曲线的影响计算结果。

图6 凸轮半径R0对抛物线过渡曲线影响

由图6a可以看出：位移曲线都交于Y轴上同一点；随着凸轮半径R0的增大，P点处的曲率半径逐渐减小，位移曲线呈现向Y轴“靠拢”的趋势。从图6b可以看出：类速度曲线为直线，且随着凸轮半径R0的增大，斜率逐渐增大；凸轮转角α为0时，类速度值始终为0，同一凸轮转角α(α≠0)下类速度的绝对值逐渐增大。从图6c可以看出：凸轮半径R0一定时，类加速度随着凸轮转角的改变保持不变；凸轮半径R0增大时，类加速度逐渐增大。

4.2.2 动程s对抛物线过渡曲线的影响

图7为动程s对抛物线过渡曲线的影响计算结果。

图7 s对抛物线过渡曲线的影响

从图7a可以看出，随着动程s逐渐增加，P点向Y轴正向移动，同时P点处的曲率半径逐渐增大。由图7b可以看出：随着凸轮转角α的增大，同一动程s下类速度的绝对值先减小后增大；随着动程s逐渐增加，类速度曲线的斜率逐渐减小；凸轮转角α为0时，类速度值始终为0；同一凸轮转角α(α≠0)下类速度的绝对值逐渐减小。由图7c可以看出：当动程s一定时，类加速度为一个固定值，不随着凸轮转角改变而变化；改变动程s，类加速度随着s的增大逐渐减小。

4.2.3 过渡角θ对抛物线过渡曲线的影响

图8为过渡角θ对抛物线过渡曲线的影响计算结果。

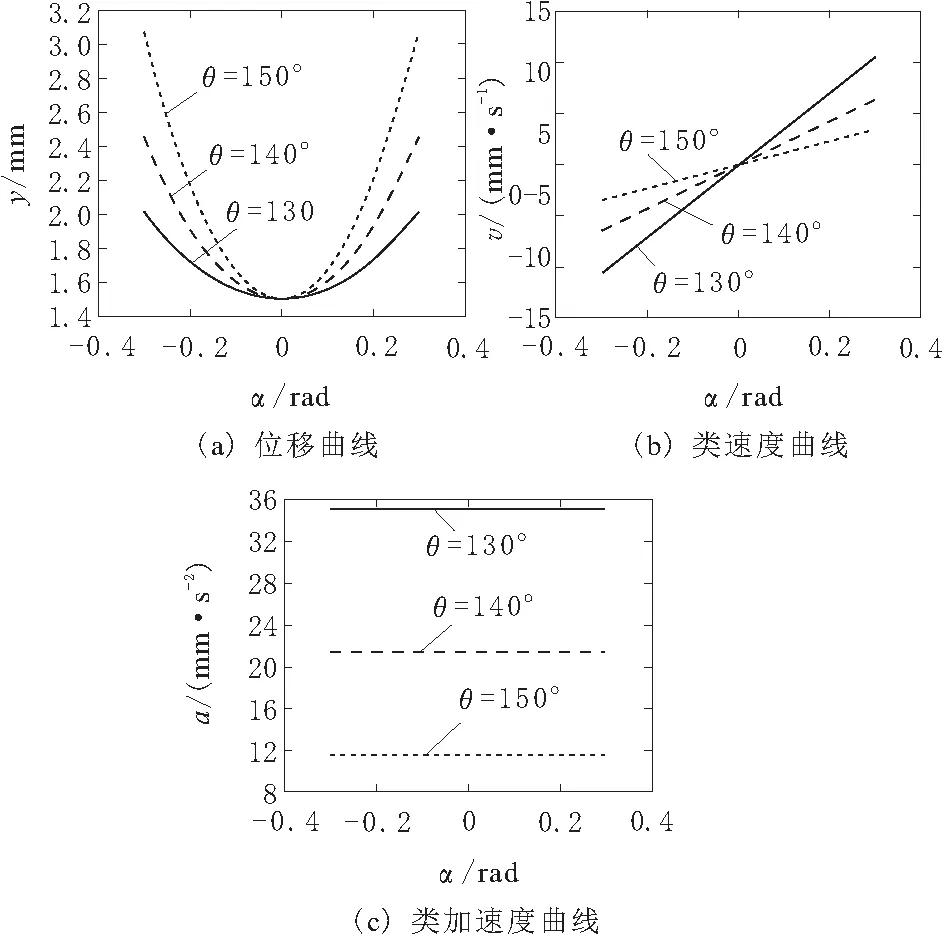
图8 θ对抛物线过渡曲线的影响

从图8a可以看出：位移曲线都交于Y轴上同一点；随着过渡角θ的增大，P点处的曲率半径逐渐增大，位移曲线呈现向Y轴“发散”的趋势。从图8b可以看出：过渡角θ增大，类速度曲线的斜率逐渐减小；当凸轮转角为0时，类速度值始终为0；同一凸轮转角α(α≠0)下类速度的绝对值逐渐减小。从图8c可以看出，类加速度不随凸轮转角改变而变化，但随着过渡角θ的增大，类加速度值逐渐下降。

4.3 五次多项式过渡曲线

4.3.1 凸轮半径R0对五次多项式过渡曲线的影响

图9为动程s对五次多项式过渡曲线的影响计算结果。

从图9a可以看出：位移曲线都交于Y轴上同一点；随着凸轮半径R0逐渐增大，P点处的曲率半径逐渐减小，M、N点处位移值逐渐增大。从图9b可以看出：在凸轮转角α为0时，类速度值均为0；随着凸轮半径R0逐渐增大，同一凸轮转角α(α≠0)下类速度的绝对值逐渐增大。从图9c可以看出：随着凸轮半径R0逐渐增加，在凸轮转角α为0时刻类加速度值均为0，选择合适的凸轮半径R0和凸轮转角α等参数值可以使M、N点处类加速度为0。

图9 R0对五次多项式过渡曲线的影响

4.3.2 动程s对五次多项式过渡曲线的影响

4）缸套水系统：本系统是由4台发动机中的缸套水（106～108℃、10 t/（h·台））分别与板式换热器A1～A4换热，换热后96℃热水汇合，经汇合后送到板式换热器B与烟气换热器，经烟气换热器升温后送至ORC机组发电，排出70℃的水与板式换热器B出水汇合回到板式换热器A1～A4重复循环。

图10为动程s对五次多项式过渡曲线的影响计算结果。

图10 s对五次多项式过渡曲线的影响

由图10a可知，随着动程s逐渐增加，P点逐渐向着Y轴正向移动，同时P点处的曲率半径逐渐增大，位移曲线在凸轮转角α为0时刻附近的小范围区域变得“扁而宽”。从图10b可以看出：在凸轮转角α为0时刻，类速度值为0；在交点附近，随着动程s逐渐增大，同一凸轮转角α(α≠0)下类速度的绝对值逐渐减小。从图10c可以看出：随着动程s逐渐增大，凸轮转角α为0时，类加速度值均为0；端点M、N处的类加速度值逐渐增大。搭配适当的凸轮转角α和动程s等参数值可使得类加速度为0。

4.3.3 过渡角θ对五次多项式过渡曲线的影响

图11为过渡角θ对五次多项式过渡曲线的影响计算结果。

图11 θ对五次多项式过渡曲线的影响

由图11a可知：位移曲线都交于Y轴上同一点；随着过渡角θ逐渐增大，P点处的曲率半径逐渐增大，M、N点处的位移值逐渐减小，位移曲线在凸轮转角α为0时刻附近的小范围区域变得“扁而宽”。由图11b可以看出，在凸轮转角α为0时，类速度值均为0，随着过渡角θ逐渐增大，同一凸轮转角α(α≠0)下类速度的绝对值逐渐减小。由图11c可知，随着过渡角θ逐渐增加，在凸轮转角α为0时刻类加速度值均为0，选择合适的参数值可以使M、N点处类加速度为0。

4.4 3种过渡曲线运动特性比较

圆弧、抛物线和五次多项式过渡曲线的运动特性如图12所示。

图12 不同形式过渡曲线

由图12a可知，3种形式过渡曲线的位移曲线均连续，避免了刚性冲击。由图12b可知：圆弧过渡曲线与抛物线过渡曲线在端点处加速度有突变，因此存在柔性冲击； 五次多项式过渡曲线在端点处加速度为0，且加速度曲线连续变化，因此避免了柔性冲击。

5 结束语

本文通过计算得到了圆弧、抛物线、五次多项式3种过渡曲线的运动特性，对比分析了不同参数对过渡曲线运动特性的影响，结论如下：

a.圆弧和抛物线过渡曲线不可避免地将会在端点处引起柔性冲击；五次多项式过渡曲线可以通过选择适当的参数值，避免在端点处产生柔性冲击，从而降低振动和噪声，保证凸轮平稳运行。

b.增大凸轮半径R0时，3种过渡曲线在M、N点处位移值均增大；类速度绝对值逐渐增大；圆弧和抛物线过渡曲线的类加速度增大。因此，在一定范围内合理地减小R0可以减小柔性冲击。

c.动程s与过渡角θ对过渡曲线运动特性的影响相似。二者增大时，3种过渡曲线与Y轴交点处曲率半径均增大；类速度绝对值逐渐减小；圆弧和抛物线过渡曲线的类加速度减小。因此，在一定范围内合理地增大s和θ可以减小柔性冲击。