基于磁钉阵列的牛舍清洁机器人导航系统研究

尚 帅，戴兴安，王锦博，宋 伟，盛守照

(1.南京航空航天大学自动化学院,江苏 南京 210016；2.中国航天科工南京晨光集团，江苏 南京 210006)

0 引言

随着工业自动化的发展，无人机器人在工业制造、农业种植、牧业养殖等场景应用得越来越广泛。如今为了提高畜牧业的生产效率，房舍集体饲养取代了以往的自然牧养。以奶牛为例主要生活在牛舍中，滞留在牛舍地面上的污物成为奶牛和人类的潜在致病源，从而极大地影响人类生命财产安全及奶牛健康和产奶量。为了适应多变的应用场景，移动机器人导航控制技术显得尤为主要。

目前，移动机器人导航的主要方法有磁导航、光学导航、激光导航和惯性导航等。许多学者也对此进行了深入的研究，季冉鸣等[1]为解决无人机器人导航问题，提出了基于磁钉及惯导系统的机器人导航控制算法；李凤娥等[2]为解决自动引导车的定位精度，系统地分析了磁钉导航产生误差的原因及解决方法；李毅等[3]为实现机器人精确定位，设计了基于机器人模型的定位导航系统。

基于此，本文以牛舍自动清洁机器人为工程研究背景，采用一种改进的机器人定位算法模型与磁钉导航技术和纯跟踪算法相结合，希望能够有效地解决机器人导航过程中的定位、累计误差等问题，使无人机器人导航在工程实践中易于实现。

1 机器人定位算法模型

本文中的清洁机器人采用三轮结构，前面1个轮子为万向轮，后面2个轮为驱动轮，采用差速转向方式。清洁机器人定位算法模型如图1所示，定义XOY为清洁机器人全局坐标系CG，定义XaOaYa为清洁机器人局部坐标系CR，机器人的实时定位信息用[x,y,ψ]来表示，其中x和y分别表示清洁机器人在全局坐标系CG下的横、纵坐标，ψ表示机器人当前的航向角。

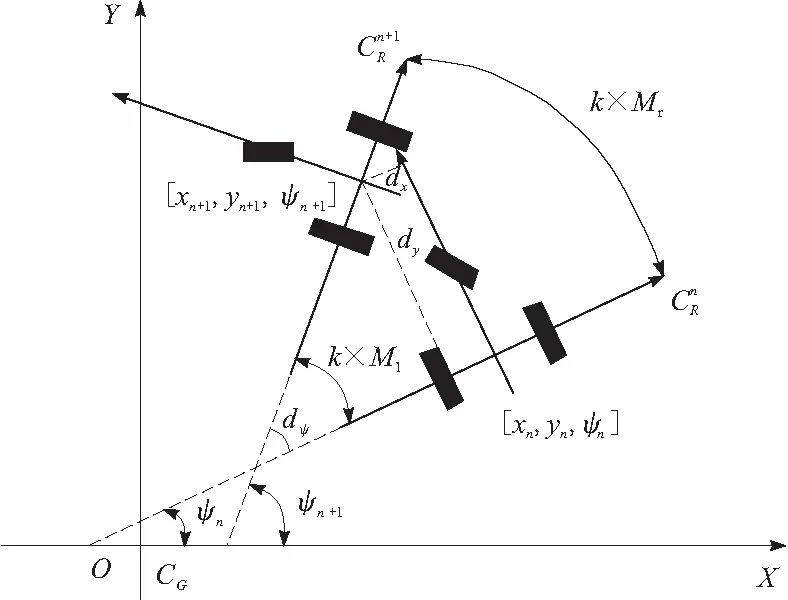
图1 清洁机器人定位算法模型

(1)

vl=k·Ml，vr=k·Mr。L为机器人2个后驱动轮的中心轮距。清洁机器人在局部坐标系CR中的x和y方向的变化量可通过前面计算出的dψ值推算出来：

(2)

(3)

机器人在局部坐标系中变化量分别为dy、dx、dψ，现把这些局部坐标系中的变化量转换为全局坐标系CG中的位置和角度信息[5]，需要进行如下变换：

ψn+1=ψn+dψ

(4)

xn+1=xn+(dx×cosψ-dysinψ)

(5)

yn+1=yn+(dx×sinψ+dycosψ)

(6)

[xn+1，yn+1，ψn+1]表示清洁机器人当前时刻的位置和角度信息，它可以由前一时刻的[xn，yn，ψn]定位信息推算，这样根据前一时刻的定位信息不断地累加就能够得到清洁机器人在清洁牛舍排泄物过程中的实时定位信息。

由于整个算法的定位信息都是根据编码器的值作为原始值来计算得到，即使选择分辨率大的编码器，长时间工作之后，累计误差还是存在的，当累计误差足够大时会导致清洁机器人无法正常定位清洁牛舍。为了保证清洁机器人能够长时间工作保证牛舍的清洁，本文采用磁钉导航修正算法来修正模型位置的累计误差。

2 清洁机器人导航控制算法

2.1 磁钉传感器位置修正算法

由于系统的所有定位信息都是由编码器的值来确定的，虽然对编码器的参数进行了矫正，但是误差仍然是存在的，在长时间的工作之后，累计误差会导致机器人无法正常定位[6]。为了对牛舍清洁机器人的航向、位置量测值的累计误差进行修正，采用在设定的移动路径上每隔一段距离铺设1个磁钉的方法，由安装在机器人上的磁传感器进行检测。为了降低后轮驱动电机对此磁传感器的影响，将磁传感器安装在机器人前端清洁铲的中间位置，垂直于车体轴线，磁传感器的中点位于机器人的中轴线上。

选用一款具有16个霍尔检测点的磁传感器[7]，检测点的间距为l=10 mm，朝清洁机器人前方看去，检测点从左到右的编号依次为1～16 。这款磁传感器的检测精度为(30±10) mm范围内N、S磁极，当传感器有m个连续点有输出时，设检测到的最左边点的编号为n，则轨道偏离中心线的偏差d的计算公式为

(7)

该算法的示意如图2所示。根据式(7)的计算结果可知：当磁钉位置偏向车体右侧的时候d为正，偏向左侧的时候d为负。

图2 磁钉导航侧偏距计算方法示意

在设定的清洁路径上每一个磁钉的全局坐标都可根据设定的磁钉间距确定，假设机器人当前状态为n，清洁机器人磁传感器检测到磁钉A时，可根据式(7)计算得到的车辆偏差d、磁传感器中心至双后轮轴中心轴线距离Lw，机器人航向ψn和磁钉A的坐标[xA,yA]对当前车辆位置进行修正，并得到当前车辆实际的位置坐标：

xn=xA-Lw×cosψn+d×sinψn

(8)

yn=yA-Lw×sinψn+d×cosψn

(9)

2.2 纯跟踪算法

全局的规划路径由一系列的路径点构成，这些路径点必须包含空间位置信息，也可以包含姿态信息，但不需要与时间有关，这些路径点被称为全局路径点。

纯跟踪算法是一种利用几何关系确定曲率的方法，该曲率将驱动车辆到达选定的路径点。牛舍清洁机器人的清洁路径比较固定，根据磁钉的铺设轨迹进行规划。由2.1节可知，磁钉的位置不变，有固定的空间位置坐标，所以在此可以把磁钉作为全局路径点来进行清洁机器人导航算法研究。

因为在实际工程应用中，为了节约成本和便于安装，磁钉的铺设密度不会很大，正常情况下2～3 m铺设1个磁钉，若该算法仅仅以磁钉作为全局路径点，由于磁钉铺设密度低，会导致控制效果较差，不能达到精度要求[8]。所以,在此提出一种虚拟路径点的方法来保证在不增大磁钉铺设密度的基础上保证控制精度。由于磁钉的坐标都已知，所以能够每2个磁钉之间等间距取一些点的坐标作为虚拟路径点，其原理如图3所示，把这些虚拟路径点和磁钉共同作为全局路径点使用。

图3 全局路径点分布示意

从双轮差速机器人模型出发，纯跟踪算法以机器人后轴为切入点，机器人的纵向车身为切线，通过控制后轮差速控制机器人转向，使得清洁机器人沿着一条可以经过全局路径点的圆弧行驶，其原理如图4所示。

图4 清洁机器人纯跟踪算法原理

假设图中的磁钉A[xA,yA]为下一个要追踪的路径点，它位于已经规划好的全局清洁路径上，现在需要控制机器人的后轴经过该路径点，ld为机器人的当前位置到目标路径点的距离即纯跟踪的前视距离，α为车身姿态到目标路径点的夹角，根据正弦定理可以推导出机器人运动所需的曲率γ。

(10)

(11)

(12)

其中，α可根据磁钉A坐标[xA,yA]与机器人当前位置坐标[xn,yn]计算得到，为

(13)

前视距离ld与机器人当前的线速度vn有关，在这里设置1个常量前视距离Lfc和1个视距系数Kd，则视距与速度的关系式为

ld=Kdvn+Lfc

(14)

双轮差速结构的车辆的速度vn与左、右轮的速度vl、vr有关，为

(15)

由式(12)得到的曲率，由式(15)得到的速度vn，和式(1)得到的角速度dψ，可以推算出当前的左、右轮转速分别为：

(16)

(17)

利用增量PID的方式对左右车轮转速进行控制[9]，控制值公式为

vn=P(en-en-1)+I·en+D(en-2en-1+en-2)

(18)

P为比例系数；I为积分系数；D为微分系数；en为当前转速误差；en-1为上一次减速误差；en-2为上上次转速误差。

根据计算得到的左右轮控制量驱动左、右2轮进行双轮差速控制，从而达到清洁机器人根据目标路径进行跟踪作业的效果。

3 机器人导航系统验证

3.1 模型验证实验

为验证清洁机器人模型准确度，如图5所示进行实物平台测试验证。

图5 清洁机器人实物验证

磁钉沿全局坐标系y轴方向排列，清洁机器人沿y轴方向走直线，设定磁钉间距分别为1 300.000 mm、2 000.000 mm，当经过1个磁钉，对y轴数据清零，将模型计算出的y轴值与实际磁钉间距做比较，机器人模型y轴验证数据如表1所示。

表1 机器人模型y轴验证数据

清洁机器人沿y轴方向做180.000°转弯，由一个磁钉转向另一个x方向平行间距为1 400.000 mm的磁钉，将模型计算出的转弯弧度及x轴行驶距离与实际的转弯弧度及x轴行驶距离做比较，机器人模型转弯弧度和x轴验证数据如表2所示。

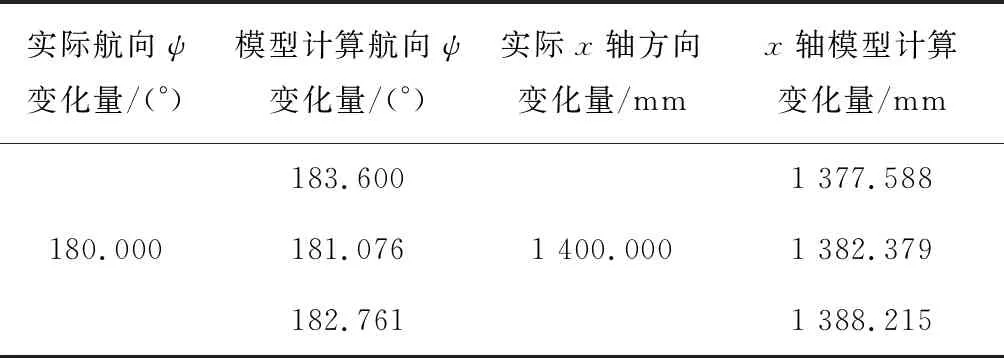
表2 机器人模型转弯弧度和x轴验证数据

由表1和表2可以看出，由模型计算得到的航向ψ变化量、x轴方向变化量、y轴方向变化量与实际测量参数对比结果显示，模型计算误差较小，而且数据稳定，模型比较可靠。

3.2 仿真实验

实验对象为双轮差速式牛舍清洁机器人。本算法利用编码器、磁传感器和机器人车辆参数进行导航控制，清洁机器人的路径有的是直线有的是曲线，根据2种不同工作路径分别仿真，直线跟踪仿真如图6所示，曲线跟踪仿真如图7所示。

图6 清洁机器人直线跟踪仿真

图7 清洁机器人曲线跟踪仿真

图6和图7中，圆点表示为磁钉，实线为机器人行驶过的路径，三角标为清洁机器人当前的目标路径点。

根据仿真结果可知，本文提出的纯跟踪磁钉修正算法在直线段的跟踪效果较好，在转弯的时候会存在一定的超调，但也能在短时间内回到预定轨迹，最终都能实现按照预定轨迹进行作业。

4 结束语

本文针对牛舍自动清洁机器人导航系统展开研究，首先，建立了机器人定位模型并对其进行了分析，然后在机器人模型的基础上，对磁钉导航策略进行研究，并引入纯跟踪(Pure Pursuit)算法完成目标跟踪及修正。最后，先将该清洁机器人在实物平台上进行模型验证，验证结果显示，与实际测量参数相比较，该模型计算误差较小，数据稳定，模型比较可靠；再对该模型进行目标路径跟踪仿真实验，仿真结果表明，所提出的纯跟踪磁钉修正算法能够实现按照预订轨迹进行作业，验证了该导航系统能引导机器人进行目标路径跟踪行驶，可以完成牛舍清洁工作。