浅谈与球有关的难点问题突破

◇ 吉林 齐威娜

在高中教材中,与球有关的知识点不多,仅涉及球的性质、表面积公式及体积公式,但在高考和竞赛中出现的球的问题都比较难,其主要原因是条件隐蔽、综合性强,对考生空间想象能力的要求较高.下面仅从三个角度,谈谈如何突破其难点.

1 从局部看整体

例1若三棱锥S-ABC的外接球半径为R,且其三条侧棱SA,SB,SC两两垂直,则SA2＋SB2＋SC2＝________.

分析观察其解题目标SA2＋SB2＋SC2的结构特点,即由“三条侧棱的平方和”可以联想到以三条侧棱为棱长的长方体的对角线的平方,而已知这三条侧棱两两垂直,进而可从“侧棱两两垂直的三棱锥”为长方体的局部看到其整体,难点得到突破.答案为4R2.

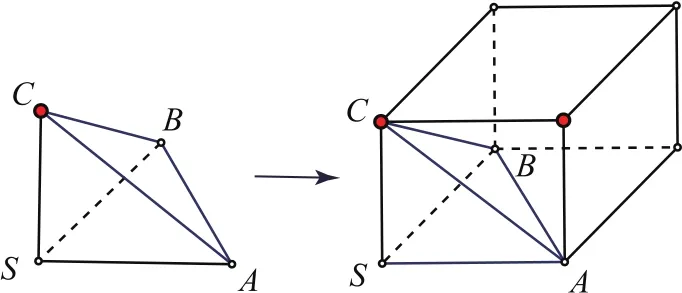
图1

由于解题目标的特殊性,本题突破难点的方式有些特别,更具一般性的突破方式是从“三条侧棱两两垂直”切入,联想到相应的长方体.比如,“已知一个三棱锥的三条侧棱两两垂直,且侧棱长为1,2,3,求其外接球半径”,这种问题只能从“侧棱两两垂直”联想到相应的长方体.对这种信息特征反应的敏感度来自日常积累的“基本活动经验”.当然,我们也可以说是先研究一个长方体,从中截取如图1的局部几何体,会得到侧棱两两垂直的三棱锥.进而可以得到另一种“基本活动经验”,即看到“侧棱两两垂直的三棱锥的外接球问题,就联想到把它恢复为长方体以后的外接球问题”.

例2在四面体ABCD中,已知AB＝CD＝,AC＝BD＝2,AD＝BC＝3,则这个四面体的外接球表面积为________.

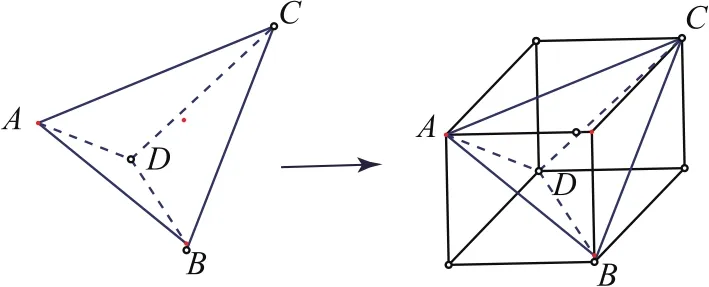
图2

分析根据例1提到的通过观察长方体的局部得到一种“基本活动经验”,即“长方体两个相对的面中,各找一条对角线,使之互相异面(比如AC与BD),就可以以它们的四个端点为顶点构成‘对棱分别相等的’四面体ABCD”,也就是看到对棱分别相等的四面体外接球问题时,我们会联想到与之相关的长方体的外接球,进而难点得到突破的.这种难点突破途径是依据“基本活动经验”,那么如何从四面体切入寻求难点突破的方式呢?根据四面体的“对棱分别相等”这个条件,我们可以进行“补形”的过程(如图3),同样可以把“局部”(四面体)转化为“整体”(长方体).根据AC＝BD＝2,取两条棱的中点,作对棱的平行线,就可以构成如图3所示的两个矩形(所在的两个平面平行),然后得到的两个矩形的八个顶点,这就形成我们要得到的长方体,但这种思维方式比起前面提到的方法更难一些.

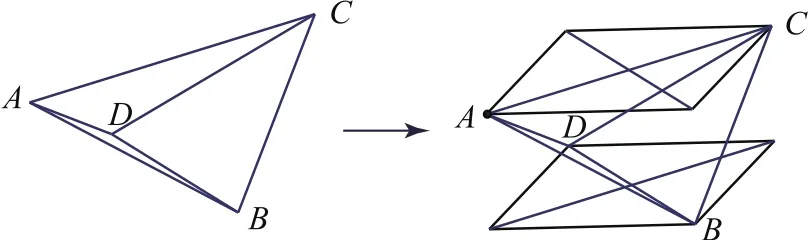
图3

解设长方体的长、宽、高分别为x,y,z,则根据题设,可得如下的三个等式:22,x2＋z2＝32,三个等式相加得x2＋y2＋z2＝10,所以此四面体的外接球表面积为10π.

2 从整体看局部

在上文中,已经展示了“从整体看局部”突破难点的方法,其原因是“割补思想方法”中,“割”与“补”是互逆的思维方式,自然就可以从“分析”和“综合”两种突破难点的方式解决与球相关的问题.但除此之外,关于球的另外一些组合体问题也需要研究突破难点的方法.这类问题的难点就是问题中不提供图形,即使提供图形,也很难从原图中直接找出突破难点的方法,所以需要依靠空间想象发现球的组合体的本质特征,再通过画出能解决问题的局部图形来突破难点.

例3侧棱长为3,底面边长为2的正三棱锥的外接球半径R＝________,其内切球半径r＝________.

分析图4中的几何体是求外接球半径的局部图形,从中又可以简化出右侧的平面图形,其中AB是其外接球的直径,O是球心,E底面的中心,易知AC⊥BC,CE⊥AB,进而得出CE2＝AE·EB,其中解得R＝.

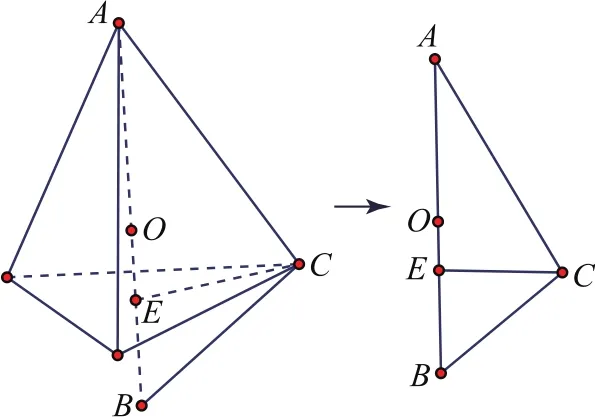
图4

由于有前面的铺垫,求内切球半径可以用“等体积法”去求得.

下面再通过转化为“等效局部图形”的方法求其内切球半径.从图5右侧的平面图形中,不难看出点E,H是球的切点,P是内切球的球心,通过相似三角形的性质,可得,解得

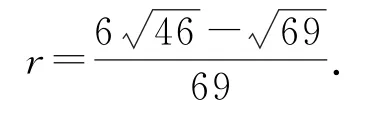
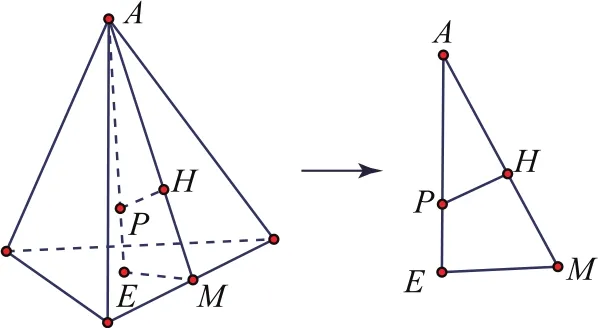
图5

对于解决正三棱锥的外接球、内切球半径问题,体现了“空间问题平面化”的立体几何中的转化思想,这种转化也起到了突破难点的作用.但正四面体作为特殊的正三棱锥,我们要掌握其性质,这样在解决有关正四面体的问题时,就可以不用作出几何图形了.

比如,正四面体的外接球和内切球的球心是重合的,同时球心将高四等分,其中外接球半径为高的内切球半径为高的,且棱长为a的正四面体的高为

例4将6个半径为r的球中的5个球放入由一个半径大于2r的球面和这个球的内接正四面体的四个面分割成的五个空间内,且此正四面体的棱长为,另一个球放入棱长为x的正八面体内,当r取得最大值时,x的最小值为________.

分析此题考查正四面体、正八面体和球的性质以及空间想象能力和转化思想.

根据题设可知,当小球的半径r取得最大值时,恰好一个小球为正四面体的内切球,其他四个小球中每个小球分别切于球面和正四面体底面中心,同时x最小时,这个小球恰好是正八面体的内切球.

根据正四面体的性质(中心将高四等分,其中内切球半径为高的),所以r取得最大值时

如图6所示,在正八面体中的Rt△AOB中,根据直角三角形中的等面积法可以得到OH·AB＝OA·OB,即,解得x＝,所以x的最小值为.

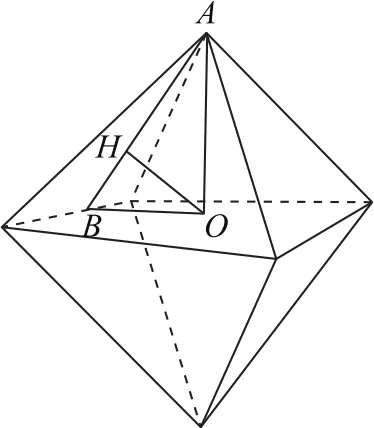
图6

由于题设中给出取得最值时,第一个图形是五个球与正四面体的组合体,其等效简图也比较难画,所以只能根据正四面体的性质,依靠空间想象求出r的最大值.而含内切球的正八面体的整体图形比较难画,所以只需要绘制其简图.

3 从局部看整体和再从整体看另一种局部

求外接球球心的位置,需要将多面体转化为能容易判断其外接球球心位置的几何体,再把这个几何体转化为能解决问题的等效的简易图形.

例5在三棱锥S-ABC中,SA⊥平面ABC,若SA＝AB＝AC＝2,BC＝23,则此三棱锥的外接球半径R＝________.

分析根据已知条件,可以判断这个三棱锥的底面是钝角三角形,所以不能转化为长方体的外接球问题,但三棱锥侧棱垂直于底面,所以可以“补”为直三棱柱的外接球问题,但这个三棱柱的底面是钝角三角形,球心在棱柱外部,进而再把柱体转化为平面图形.

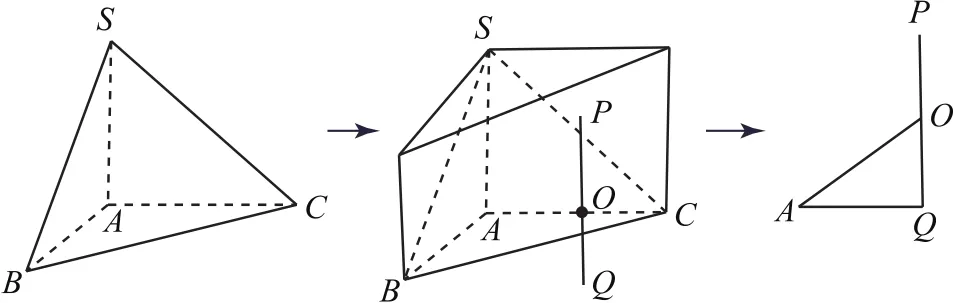
图7

图7中P,Q分别为三棱柱上、下底面的外接圆的圆心,O为外接球的球心,根据已知条件及余弦定理和正弦定理知解得AQ＝2,所以

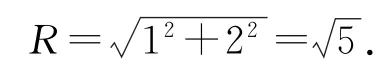
通过这个例题可以发现,关于四面体的外接球问题,从更具一般性的角度去分析,突破难点的方式就是将问题转化为棱柱的外接球问题.

以上三种突破难点的方法,本质上是两种,第三种属于前两种的融合,不管用哪种方法突破难点,我们最后突破难点的结果是明确了球心的位置.需要强调的是以上三种突破难点的方式体现了立体几何中重要的一种数学思想和方法,即“割补法”,也体现了数学核心素养中的“直观想象”和“逻辑推理”及四基“基础知识、基本技能、基本思想和基本活动经验”.