对高考中平面向量试题特点的分析
2021-01-11北京韩静波
◇ 北京 韩静波
向量是近代数学中重要和基本的数学概念之一,它是沟通代数、几何和三角函数的一种工具,有着极其丰富的实际背景.在高中阶段,向量问题灵活多变,解决向量问题既要求透彻理解概念,又需要掌握解决相关问题的通性通法,还要有数学思想的引领.本文通过对高考试题的分析,总结在平面向量教与学中应该重视的问题.
1 注重概念的理解和知识的系统性
数学概念是数学基础知识的核心,是学好数学知识和培养数学能力的基础.对于高中学生而言,向量是一种新的数学研究对象,很多概念都可从数和形两种角度理解,并且有多种不同表现形式,另外概念间相互联系形成网络,因此在平面向量的教与学中应该注重概念的理解和知识的系统性.
例1(2017年北京卷理6)设m,n为非零向量,则“存在负数λ,使得m=λn”是“m·n<0”的( ).
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
分析解答此题的关键是理解“存在负数λ,使得m=λn”和“m·n<0”的本质分别是什么.考查了向量共线(向量平行)、向量的数乘、向量的夹角、向量的数量积等概念,也就是考查是否理解相关概念的本质以及是否形成了知识体系,考查了转化与化归思想以及逻辑推理能力.
解存在负数λ,使得m=λn⇔m与n方向相反.因为m,n为非零向量,所以|m|≠0且|n|≠0.
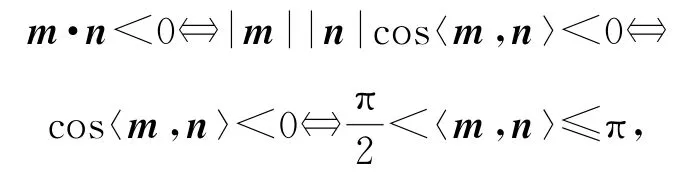
得出m与n方向相反或夹角为钝角.所以“存在负数λ,使得m=λn”是“m·n≤0”.故选 A.
点评
解决此题需要准确理解向量共线(向量平行)、向量的数乘、向量的夹角、向量的数量积等概念,并掌握相关概念间的关系,例如,对于非零向量a,b,a∥b⇔存在唯一非零实数λ,a=λb⇔a,b的夹角为0或π,其中a,b同向⇔存在唯一正实数λ,a=λb⇔a,b的夹角为0,a,b反向⇔存在唯一负实数λ,a=λb⇔a,b的夹角为π.由此可以看出,平面向量的教与学应该注重概念的理解和知识的系统性.
2 注重通性通法和方法的全面性
平面向量问题的问题情境新颖多变,但从基本概念出发,会发现问题的本质不变,解决问题的思想方法也是不变的,因此要全面透彻地理解解决相关问题的通性通法.通性通法是高考考查的重点,要学会用通性通法解决平面向量问题.
例2(2020年北京卷3)已知正方形ABCD的边长为2,点P满足.
分析解答此题的关键是根据向量的线性运算由分析出P的位置,再根据向量的数量积运算求解.旨在考查学生是否全面地掌握了解决向量的线性运算和向量的数量积运算的通性通法,考查了数形结合和转化与化归思想以及逻辑推理能力.
解先求.
解法1从“形”的角度
如图1所示,根据向量加法的平行四边形法则,以线段AB,AC为邻边作平行四边形ABP′C,则因为平行四边形ABP′C对角线AP′与BC互相平分,所以点P为BC的中点.
也可以从另一个角度证明点P为边BC的中点.如图2所示,设点B′,C′分别为线段AB,AC的中点,所以则线段AP是以线段AB′,AC′为邻边的平行四边形的对角线,所以点P为边BC的中点.

图1

图2
解法2从“坐标”的角度
建立平面直角坐标系,如图3所示,则A(0,0),B(2,0),C(2,2),D(0,2),所以(2,1).
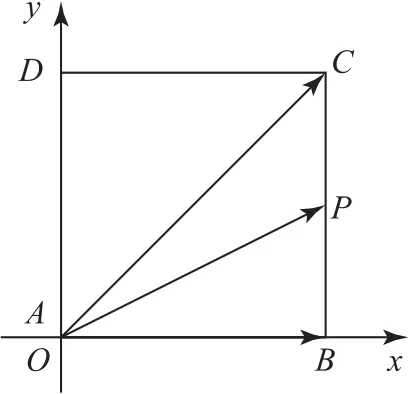
图3
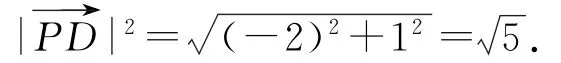
解法1从“形”的角度.
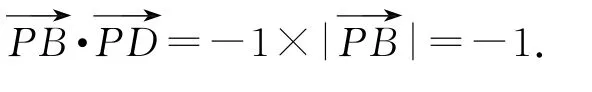
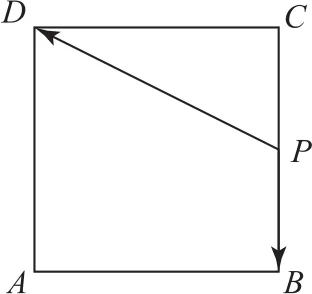
图4
解法2从“坐标”的角度.

解法3从“代数”角度.

或

点评
一般而言,解决平面向量问题可以从“数”和“形”两个角度考虑,此题所求的是平面向量的数量积,解决此类问题可以用数量积的几何意义(关键在于投影),也可用坐标法(关键在建系),还可以用定义法(关键在转化).由高考题可以看出,平面向量的教与学应该注重通性通法,而且方法不能只掌握一种,要全面.
3 注重数形结合思想
对于向量问题,要善于从“数”和“形”两个角度考虑问题,尤其要有“形”的意识,要善于利用直观想象将抽象的符号直观化为图形,但当从几何角度不易求解时,也要能利用代数方法求解.
例3(2020年上海卷12)已知a1,a2,b1,b2,…,bk(k∈N∗)是平面内两两互不平等的向量,满足|a1-a2|=1,且|ai-bj|∈{1,2}(其中i=1,2,j=1,2,…,k),则k的最大值为________.
分析解答此题的关键是从“形”的角度理解|a1-a2|=1,|ai-bj|∈{1,2},并将其翻译为图形语言.考查了相等向量、向量的减法和向量的模,考查了数形结合和转化与化归思想以及直观想象能力.
解任意取一点O(不妨设为坐标原点),分别作bk(k∈N∗).
不妨设A1(1,0),A2(2,0).由|ai-bj|∈{1,2},得,即Bj到A1和A2的距离都为1或2(j=1,2,…,k).
所以Bj是分别以A1和A2为圆心,半径分别为1,1的圆交点,或分别以A1和A2为圆心,半径分别为1,2的圆交点,或分别以A1和A2为圆心,半径分别为2,1的圆交点,或分别以A1和A2为圆心,半径分别为2,2的圆交点 (j=1,2,…,k).
以A1和A2为圆心,半径分别为1,1的圆交点有2个(如图5);以A1和A2为圆心,半径分别为1,2的圆交点有1个(如图6);以A1和A2为圆心,半径分别为2,1的圆交点有1个(如图7);分别以A1和A2为圆心,半径分别为2,2的圆交点有2个(如图8).所以k的最大值为6.
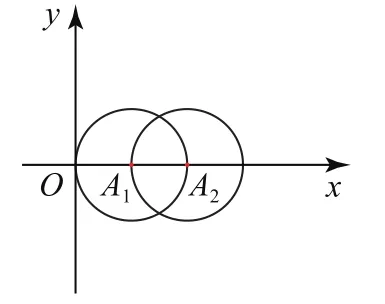
图5
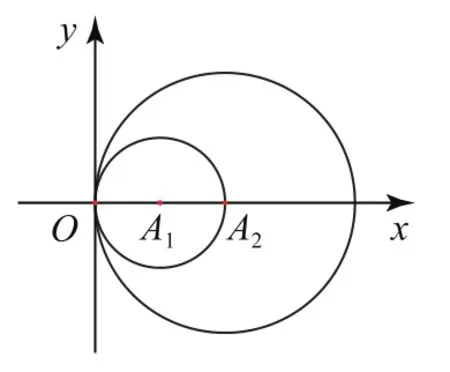
图6
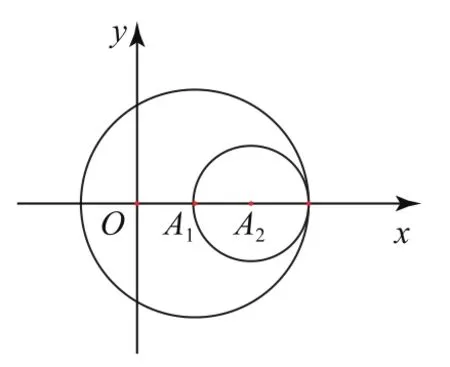
图7

图8
例4(2020年天津卷15)如图9所示,在四边形ABCD中,∠B=60°,AB=3,BC=6,且,则实数λ的值为________;若M,N是线段BC上的动点,且的最小值为________.
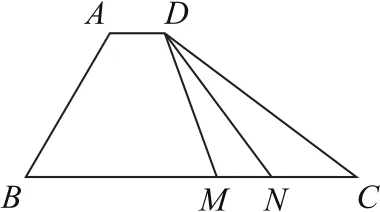
图9
分析此题考查的是向量的数量积,与例3一样可以从向量数量积的几何意义、坐标以及定义三个方面考虑,但此题从几何角度不易解决此题,考查了相等向量、向量的减法和向量的模,考查了数形结合思想以及逻辑推理能力.
解由已知得,所以.

图10
如图10所示,以B原点,以BC所在直线为x轴建立平面直角坐标系,则.不妨设M在N的左侧时,M(x,0),则

此二次函数开口向上,对称轴为x=2∈[0,5].所以当x=2时,取得最小值.
点评
上面两道高考题,例3从“形”的角度,容易发现问题本质,而例4考查的是平面向量数量积运算.解决此类问题可以从三个方面考虑,但例4不易从利用数量积几何意义解决,因此考虑利用坐标.由高考题可以看出,平面向量的教与学应该注重数形结合思想,对于一些情境新颖、较复杂的问题,尤其要善于从“形”的角度思考问题本质,但从“形”的角度不易解决问题时,也要能利用代数方法求解.
4 注重转化与化归的思想
在解决平面向量问题时,经常利用向量的线性运算将“不好”的向量转化为“好”的向量,有时,也会在问题中选择两个不共线的“好”向量作为基底,将问题中所有的向量都用这组基底表示,就能化未知为已知,化复杂为简单.从本质上,向量的坐标形式就是由此推导出的.

图11
例5(2020年江苏卷13)在△ABC中,AB=4,AC=3,∠BAC=90°,D 在边BC上,延长AD到P,使得AP=9,若(m为常数),则CD的长度是________.
分析解答此题的关键是根据向量的线性运算处理直接根据该式子构造平行四边形或三角形比较困难,所以可以考虑坐标法,也可考虑将所有向量用基底表示.考查的是向量的线性运算,考查了数形结合和转化与化归思想以及逻辑推理能力.
解法1如图12所示,以A原点,分别以AB,AC所在直线为x轴,y轴建立平面直角坐标系,则A(0,0),B(4,0),C(0,3).
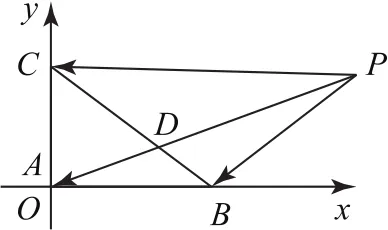
图12


点评
解法1利用数形结合思想,从“数”的角度将问题坐标化.解法2是利用转化与化归思想,选择“好”向量作为基底,将所有向量用这组基底表示,将问题转化为简单的问题.由高考题可以看出,平面向量的教与学应该注重转化与化归思想,对于一些情境新颖、较复杂的问题,可以考虑将“不好”的向量转化为“好”的向量.
高考数学试卷是数学教与学的一个指挥棒,它通过一道道题目引导如何进行数学教学和学习.通过对高考试卷中平面向量问题的分析,总结出平面向量的教与学要注重概念的理解和知识的系统性,注重通性通法和方法的全面性,注重数形结合思想,注重转化与化归的思想.
