明确目标是要务 先猜后证是良策

◇ 北京 范方兵 王芝平(特级教师)

解析几何既是高考的重点,也是高考的难点.在解答解析几何题目时,往往会在某一步中思路受阻,不知该如何往下进行,迷失了解题的方向,有时即使能继续往下计算,运算量也非常大.因此,在解题中找到解题的目标是首要任务,目标明确后,再考虑如何简化运算.

我们知道,普遍性寓于特殊性之中,并通过特殊性表现出来,没有特殊性就没有普遍性,一个命题在一般情形下成立,那么它在特殊情形下也成立.为了明确解题目标、降低运算量、提高运算速度,对具有一般性结论的题目,若能发现题设条件具有某种特殊的数量关系或所给图形具有某种特征时,可选取恰当的特殊元素(特殊点、特殊值、特殊图形、特殊例子)进行简单的运算、推理或判断.

我们大致有两个途径来寻求解题目标:一是作出符合题目要求的示意图,通过图形的直观性先猜后证,实际上,很多时候只要作出大致准确的示意图,其结论就不难猜测;二是从特殊情形去算一算,通过特殊情形的结论,猜测一般情形的结论.下面以一道高考试题来进行具体说明,希望对读者有所帮助.

1 试题再现

题目(2020年全国卷Ⅰ文21理20)已知A,B分别为椭圆E的左、右顶点,G为E的上顶点,为直线x＝6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.

(1)求E的方程;

(2)证明:直线CD过定点.

2 解法分析

(2)思路1设P(6,p),则直线PA的方程为

所以

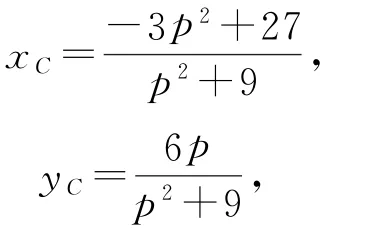
即

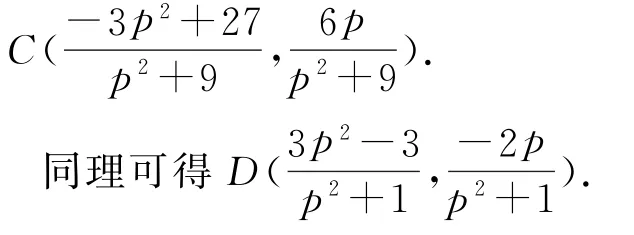
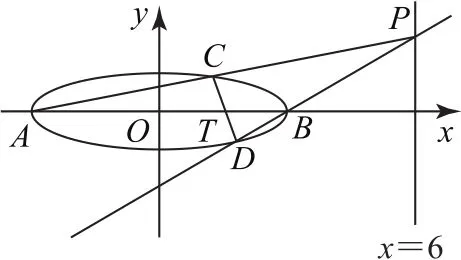
图1

由对称性可知,直线CD若过定点,则该定点必在x轴上.设定点为T(t,0),则

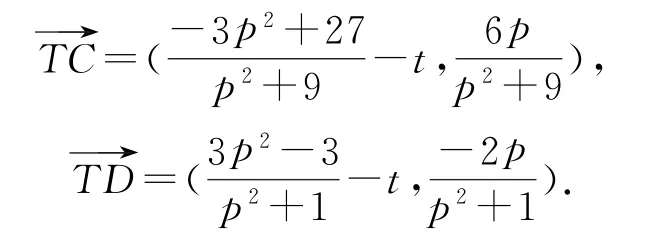
因为C,T,D三点共线,所以

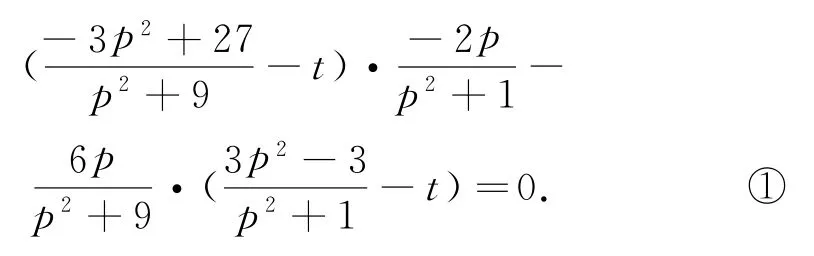
如果感觉上述方程比较难解,那么还有没有别的方法呢?实际上,着眼于“特殊性探路,一般性证明”的思路,我们在式①中可以取p＝1,不难得到再证明时,式①成立,运算难度就降下来了.

思路2因为两点确定一条直线,所以C,D两点坐标会满足关于x,y的同一个一次方程,这个方程对应的直线过定点即可.

设P(6,p),C(x1,y1),D(x2,y2).当p≠0时,x1≠3,x2≠－3.因为A,C,P三点共线,所以kAC＝,得

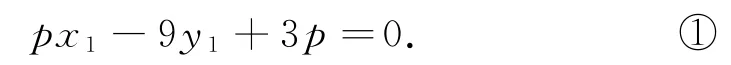
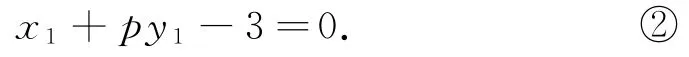
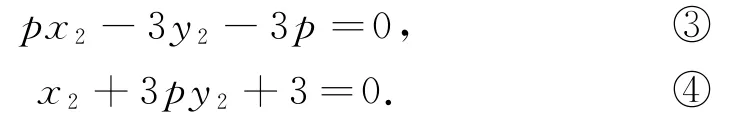
①②表示点C的坐标所满足的方程,③④表示点D的坐标所满足的方程.

同理,可以得到③×3＋④×p,得4px2＋(3p2－9)y2－6p＝0.因此,直线CD的方程为4px＋(3p2－9)y－6p＝0,恒过点.当p＝0时,直线CD与x轴重合,必过点.

思路3设P(6,p),当p≠0时,x1≠3,x2≠－3,y1≠y2.若x1≠x2,直线CD的方程为y－y1＝,整理得.

于是,只需要证明

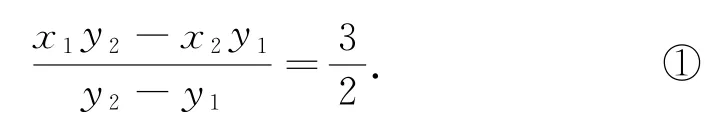
这是一个关于x1,x2,y1,y2的等式,我们希望利用点的坐标对几何关系的刻画,来证得等式成立.

首先,我们刻画点P是直线AC与BD的交点.

由A,C,P三点共线,知

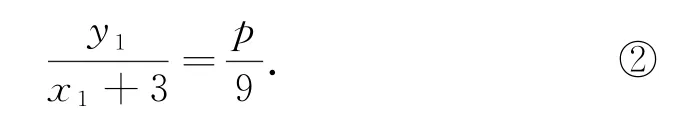
由D,B,P三点共线,知

因为①中只含x1,x2,y1,y2四个量,因此由式②③,消去p,得到整理得

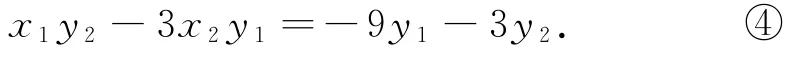
这个结果离①还有点远,其原因是点C,D在椭圆上还没有得到刻画,于是我们就从这里入手.

3 解后反思

2)思路2中,在得到式①②③④后,如果没有解题目标“直线CD过定点的指引,那么下一步该干什么就会迷失方向,代数运算的难度也会很大,很可能会进行毫无目的的凑配.有了目标的指引,既清晰了解题思路,又使得代数运算有了思维的固着点,是一种清晰、生动的思维活动,而不是烦琐的尝试,真正体现了“代数运算表其外,几何性质蕴其中”.

3)思路3也是基于对解题目标“直线CD过定点”的探索、猜想,得到了待证目标后面的代数变形都是围绕这个目标来进行,使得整个解题过程一气呵成.本题考查学生动手探索、转化与化归的数学能力,在平时的教学中,教师要引导学生动手实践,根据图形直观、特殊情形,对所求结论进行大胆猜想,从而明确解题目标,选择简捷、合理的方法进行推理、计算,真正让学生体会在解析几何解题过程中“明确目标是要务,先猜后证是良策”.

4)本题以射影几何中有关极点、极线的理论为基础,背景深刻,设问精巧,考查解决解析几何问题的一般思路与方法,考查数学运算、逻辑推理等数学核心素养.本题也可以基于极点、极线的理论,在双曲线、抛物线中进行结论的相应拓展,限于篇幅,不再赘述.